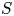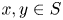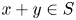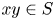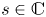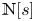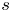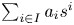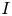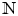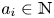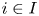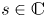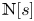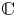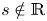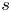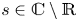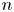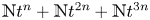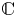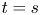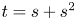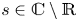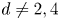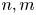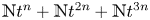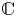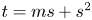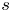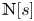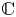1. Introduction
As in [Reference Kiss, Somlai and Terpai16], we say that a nonempty set of complex numbers $S \subseteq {\mathbb {C}}$![]() is invariant if it is closed under addition and multiplication. Equivalently, an invariant set $S$
is invariant if it is closed under addition and multiplication. Equivalently, an invariant set $S$![]() is the set which is both an additive semigroup and a multiplicative semigroup, namely, for all $x, y \in S$
is the set which is both an additive semigroup and a multiplicative semigroup, namely, for all $x, y \in S$![]() we have $x+y \in S$
we have $x+y \in S$![]() and $xy \in S$
and $xy \in S$![]() . Evidently, the set $\{0\}$
. Evidently, the set $\{0\}$![]() is invariant. Any other invariant set $S \ne \{0\}$
is invariant. Any other invariant set $S \ne \{0\}$![]() is infinite and unbounded, since for any nonzero $s \in S$
is infinite and unbounded, since for any nonzero $s \in S$![]() we have $ns \in S$
we have $ns \in S$![]() for each positive integer $n$
for each positive integer $n$![]() .
.
For the purposes of this paper, we let ${\mathbb {N}}$![]() be the set of positive integers, and ${\mathbb {N}}_0$
be the set of positive integers, and ${\mathbb {N}}_0$![]() be the set of non-negative integers. That is ${\mathbb {N}}$
be the set of non-negative integers. That is ${\mathbb {N}}$![]() does not include $0$
does not include $0$![]() , whereas ${\mathbb {N}}_0$
, whereas ${\mathbb {N}}_0$![]() does include $0$
does include $0$![]() .
.
It is clear that for each $s \in {\mathbb {C}}$![]() the smallest invariant set containing $s$
the smallest invariant set containing $s$![]() is the set
is the set

where $I$![]() runs over all finite nonempty subsets of ${\mathbb {N}}$
runs over all finite nonempty subsets of ${\mathbb {N}}$![]() and $a_i \in {\mathbb {N}}$
and $a_i \in {\mathbb {N}}$![]() for each $i \in I$
for each $i \in I$![]() . Indeed, if $s$
. Indeed, if $s$![]() belongs to some invariant set $S$
belongs to some invariant set $S$![]() , then each element of ${\mathbb {N}}[s]$
, then each element of ${\mathbb {N}}[s]$![]() must belong to the set $S$
must belong to the set $S$![]() as well, so ${\mathbb {N}}[s] \subseteq S$
as well, so ${\mathbb {N}}[s] \subseteq S$![]() . Furthermore, the set ${\mathbb {N}}[s]$
. Furthermore, the set ${\mathbb {N}}[s]$![]() defined in (1.1) is closed under addition and multiplication and so is invariant.
defined in (1.1) is closed under addition and multiplication and so is invariant.
If in (1.1) the coefficients $a_i$![]() belong not to ${\mathbb {N}}$
belong not to ${\mathbb {N}}$![]() but to the set of integers ${\mathbb {Z}}$
but to the set of integers ${\mathbb {Z}}$![]() and $I$
and $I$![]() runs over all nonempty subsets of the set ${\mathbb {N}}_0$
runs over all nonempty subsets of the set ${\mathbb {N}}_0$![]() , then the corresponding set is simply ${\mathbb {Z}}[s]=\{P(s)\}$
, then the corresponding set is simply ${\mathbb {Z}}[s]=\{P(s)\}$![]() , where $P$
, where $P$![]() run over all elements of the ring of polynomials ${\mathbb {Z}}[x]$
run over all elements of the ring of polynomials ${\mathbb {Z}}[x]$![]() . A very similar quantity ${\mathbb {N}}_0[s]$
. A very similar quantity ${\mathbb {N}}_0[s]$![]() , where $a_i \in {\mathbb {N}}$
, where $a_i \in {\mathbb {N}}$![]() in (1.1) and $I$
in (1.1) and $I$![]() is a subset of ${\mathbb {N}}_0$
is a subset of ${\mathbb {N}}_0$![]() (so a free positive coefficient is also allowed), has been recently investigated in [Reference Ajran, Bringas, Li, Singer and Tirador2], [Reference Correa-Morris and Gotti6]. There, it is called an evaluation polynomial semiring at $s$
(so a free positive coefficient is also allowed), has been recently investigated in [Reference Ajran, Bringas, Li, Singer and Tirador2], [Reference Correa-Morris and Gotti6]. There, it is called an evaluation polynomial semiring at $s$![]() . Obviously, for each $s \in {\mathbb {C}}$
. Obviously, for each $s \in {\mathbb {C}}$![]() , we have
, we have
Various problems related to invariant subsets of the set of real numbers ${\mathbb {R}}$![]() have been considered in [Reference Elekes and Keleti12], [Reference Kiss, Somlai and Terpai16] and also recently in [Reference Dubickas10]. In particular, in [Reference Dubickas10, Theorem 2] we showed that if an invariant set $S$
have been considered in [Reference Elekes and Keleti12], [Reference Kiss, Somlai and Terpai16] and also recently in [Reference Dubickas10]. In particular, in [Reference Dubickas10, Theorem 2] we showed that if an invariant set $S$![]() contains a real negative element, which is not in ${\mathbb {Z}}$
contains a real negative element, which is not in ${\mathbb {Z}}$![]() , then $S$
, then $S$![]() is everywhere dense in ${\mathbb {R}}$
is everywhere dense in ${\mathbb {R}}$![]() . Of course, these two conditions are also necessary for the density of ${\mathbb {N}}[s]$
. Of course, these two conditions are also necessary for the density of ${\mathbb {N}}[s]$![]() in ${\mathbb {R}}$
in ${\mathbb {R}}$![]() , since ${\mathbb {N}}[s] \subseteq [0, +\infty )$
, since ${\mathbb {N}}[s] \subseteq [0, +\infty )$![]() for $s \geq 0$
for $s \geq 0$![]() and ${\mathbb {N}}[s] \subseteq {\mathbb {Z}}$
and ${\mathbb {N}}[s] \subseteq {\mathbb {Z}}$![]() for $s \in {\mathbb {Z}}$
for $s \in {\mathbb {Z}}$![]() . Therefore, in the present notation (with ${\mathbb {N}}[s]$
. Therefore, in the present notation (with ${\mathbb {N}}[s]$![]() as in (1.1)) we can write [Reference Dubickas10, Theorem 2] as follows:
as in (1.1)) we can write [Reference Dubickas10, Theorem 2] as follows:
Theorem 1.1 For $s \in {\mathbb {R}}$![]() the set ${\mathbb {N}}[s]$
the set ${\mathbb {N}}[s]$![]() is everywhere dense in ${\mathbb {R}}$
is everywhere dense in ${\mathbb {R}}$![]() if and only if $s<0$
if and only if $s<0$![]() and $s \notin {\mathbb {Z}}$
and $s \notin {\mathbb {Z}}$![]() .
.
A similar density in ${\mathbb {R}}$![]() results for the set polynomials evaluated at a given point $s \in {\mathbb {R}}$
results for the set polynomials evaluated at a given point $s \in {\mathbb {R}}$![]() whose coefficients belong to some finite subsets of the set ${\mathbb {Z}}$
whose coefficients belong to some finite subsets of the set ${\mathbb {Z}}$![]() were obtained in [Reference Drobot and McDonald8], [Reference Peres and Solomyak20], [Reference Sidorov and Solomyak21] and in several subsequent papers related to the problem earlier raised by Erdős, Joo and Komornik. Its solution has been finally given by Feng [Reference Feng13].
were obtained in [Reference Drobot and McDonald8], [Reference Peres and Solomyak20], [Reference Sidorov and Solomyak21] and in several subsequent papers related to the problem earlier raised by Erdős, Joo and Komornik. Its solution has been finally given by Feng [Reference Feng13].
In this paper, we investigate the set ${\mathbb {N}}[s]$![]() for $s \in {\mathbb {C}} \setminus {\mathbb {R}}$
for $s \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() . We will prove the following:
. We will prove the following:
Theorem 1.2 For $s \in {\mathbb {C}}$![]() the set ${\mathbb {N}}[s]$
the set ${\mathbb {N}}[s]$![]() is everywhere dense in ${\mathbb {C}}$
is everywhere dense in ${\mathbb {C}}$![]() if and only if $s \notin {\mathbb {R}}$
if and only if $s \notin {\mathbb {R}}$![]() and $s$
and $s$![]() is not a complex quadratic algebraic integer.
is not a complex quadratic algebraic integer.
Of course, if $s \in {\mathbb {R}}$![]() then ${\mathbb {N}}[s] \subset {\mathbb {R}}$
then ${\mathbb {N}}[s] \subset {\mathbb {R}}$![]() , while if $s$
, while if $s$![]() is a complex quadratic algebraic integer then ${\mathbb {N}}[s]$
is a complex quadratic algebraic integer then ${\mathbb {N}}[s]$![]() is a subset of the lattice ${\mathbb {Z}}+{\mathbb {Z}} s$
is a subset of the lattice ${\mathbb {Z}}+{\mathbb {Z}} s$![]() , and so is not dense in ${\mathbb {C}}$
, and so is not dense in ${\mathbb {C}}$![]() . Therefore, avoiding both these situations for $s$
. Therefore, avoiding both these situations for $s$![]() is indeed necessary for the density of ${\mathbb {N}}[s]$
is indeed necessary for the density of ${\mathbb {N}}[s]$![]() in ${\mathbb {C}}$
in ${\mathbb {C}}$![]() . The nontrivial part in the proof of theorem 1.2 is to show that for any other $s \in {\mathbb {C}}$
. The nontrivial part in the proof of theorem 1.2 is to show that for any other $s \in {\mathbb {C}}$![]() the set ${\mathbb {N}}[s]$
the set ${\mathbb {N}}[s]$![]() is everywhere dense in ${\mathbb {C}}$
is everywhere dense in ${\mathbb {C}}$![]() .
.
It is known that if $s \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() is an algebraic number, which is not a quadratic algebraic integer, then the set ${\mathbb {Z}}[s]$
is an algebraic number, which is not a quadratic algebraic integer, then the set ${\mathbb {Z}}[s]$![]() is everywhere dense in ${\mathbb {C}}$
is everywhere dense in ${\mathbb {C}}$![]() ; see, e.g., [24]. An even stronger result for algebraic $s$
; see, e.g., [24]. An even stronger result for algebraic $s$![]() of degree at least $3$
of degree at least $3$![]() can be derived from [Reference Conrad5, Theorem 0.1]. However, the set ${\mathbb {N}}[s]$
can be derived from [Reference Conrad5, Theorem 0.1]. However, the set ${\mathbb {N}}[s]$![]() is the smallest of the three sets considered in (1.2), so the density of ${\mathbb {Z}}[s]$
is the smallest of the three sets considered in (1.2), so the density of ${\mathbb {Z}}[s]$![]() does not imply the density of ${\mathbb {N}}[s]$
does not imply the density of ${\mathbb {N}}[s]$![]() . In addition, we are interested not only in algebraic but also in transcendental $s$
. In addition, we are interested not only in algebraic but also in transcendental $s$![]() .
.
In fact, for most $s$![]() our result is much more precise. We will show that in order to get a set dense in ${\mathbb {C}}$
our result is much more precise. We will show that in order to get a set dense in ${\mathbb {C}}$![]() it is sufficient to use just three powers of $s$
it is sufficient to use just three powers of $s$![]() or $s+s^2$
or $s+s^2$![]() for $s$
for $s$![]() transcendental or three powers of $ms+s^2$
transcendental or three powers of $ms+s^2$![]() with some $m \in {\mathbb {N}}$
with some $m \in {\mathbb {N}}$![]() for $s$
for $s$![]() algebraic of degree $d \ne 2, 4$
algebraic of degree $d \ne 2, 4$![]() with appropriate coefficients from ${\mathbb {N}}$
with appropriate coefficients from ${\mathbb {N}}$![]() :
:
Theorem 1.3 Let $s \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() be a transcendental number. Then, there is a positive integer $n$
be a transcendental number. Then, there is a positive integer $n$![]() such that the sumset
such that the sumset
is everywhere dense in ${\mathbb {C}}$![]() for either $t=s$
for either $t=s$![]() or $t=s+s^2$
or $t=s+s^2$![]() .
.
Similarly, if $s \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() is an algebraic number of degree $d \notin \{2, 4\}$
is an algebraic number of degree $d \notin \{2, 4\}$![]() then there exist $n, m \in {\mathbb {N}}$
then there exist $n, m \in {\mathbb {N}}$![]() such that the sumset (1.3) is everywhere dense in ${\mathbb {C}}$
such that the sumset (1.3) is everywhere dense in ${\mathbb {C}}$![]() for $t=ms+s^2$
for $t=ms+s^2$![]() .
.
Theorem 1.3 implies the sufficiency part of theorem 1.2 for $s \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() , except for the case when $s$
, except for the case when $s$![]() is an algebraic number of degree $2$
is an algebraic number of degree $2$![]() or $4$
or $4$![]() , because the sumset (1.3) is a subset of ${\mathbb {N}}[s]$
, because the sumset (1.3) is a subset of ${\mathbb {N}}[s]$![]() (see (1.1)).
(see (1.1)).
We stress that in the sumset (1.3) it should be at least three terms, because for any two complex numbers $s_1, s_2$![]() the sumset
the sumset
is contained in a lattice or in a line. Therefore, it cannot be dense in ${\mathbb {C}}$![]() . In terms of semigroups, this observation combined with theorem 1.3 implies that, for $s \in {\mathbb {C}} \setminus {\mathbb {R}}$
. In terms of semigroups, this observation combined with theorem 1.3 implies that, for $s \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() , which is not an algebraic number of degree $2$
, which is not an algebraic number of degree $2$![]() or $4$
or $4$![]() , the smallest finitely generated additive semigroup $A \subset {\mathbb {N}}[s]$
, the smallest finitely generated additive semigroup $A \subset {\mathbb {N}}[s]$![]() that is everywhere dense in ${\mathbb {C}}$
that is everywhere dense in ${\mathbb {C}}$![]() is of rank $3$
is of rank $3$![]() .
.
Evidently, no algebraic number $s \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() can be of degree $d=1$
can be of degree $d=1$![]() . For $s \in {\mathbb {C}} \setminus {\mathbb {R}}$
. For $s \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() of degree $d=2$
of degree $d=2$![]() and any $s_1, \dots, s_k \in {\mathbb {N}}[s]$
and any $s_1, \dots, s_k \in {\mathbb {N}}[s]$![]() there is positive integer $q$
there is positive integer $q$![]() (depending on $s, s_1, \dots, s_k$
(depending on $s, s_1, \dots, s_k$![]() only) such that
only) such that
Therefore, the sumset
is not dense in ${\mathbb {C}}$![]() . So, for algebraic $s \in {\mathbb {C}} \setminus {\mathbb {R}}$
. So, for algebraic $s \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() of degree $d=2$
of degree $d=2$![]() , we cannot expect a result of the same type as that in theorem 1.3 (not only with sumset of three sets as in (1.3) but also with sumset of $k$
, we cannot expect a result of the same type as that in theorem 1.3 (not only with sumset of three sets as in (1.3) but also with sumset of $k$![]() sets). However, for those numbers the density problem as claimed in theorem 1.2 can be settled by the following result which completes the case of algebraic $s$
sets). However, for those numbers the density problem as claimed in theorem 1.2 can be settled by the following result which completes the case of algebraic $s$![]() of degree $d=2$
of degree $d=2$![]() :
:
Theorem 1.4 If $s \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() is a quadratic algebraic number then the set ${\mathbb {N}}[s]$
is a quadratic algebraic number then the set ${\mathbb {N}}[s]$![]() is everywhere dense in ${\mathbb {C}}$
is everywhere dense in ${\mathbb {C}}$![]() if and only if $s$
if and only if $s$![]() is not an algebraic integer.
is not an algebraic integer.
The case of algebraic $s$![]() of degree $d=4$
of degree $d=4$![]() is not considered in theorem 1.3 for a similar reason. It turns out that theorem 1.3 does not hold for some very special quartic algebraic numbers $s$
is not considered in theorem 1.3 for a similar reason. It turns out that theorem 1.3 does not hold for some very special quartic algebraic numbers $s$![]() .
.
We say that $s \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() is an exceptional number if it is an algebraic number of degree $d=4$
is an exceptional number if it is an algebraic number of degree $d=4$![]() over ${\mathbb {Q}}$
over ${\mathbb {Q}}$![]() and there is a real quadratic number field $E$
and there is a real quadratic number field $E$![]() such that
such that
Of course, at least one of the numbers $\psi, \lambda$![]() in (1.5) must be irrational, since otherwise $s$
in (1.5) must be irrational, since otherwise $s$![]() , as a nonreal root of the polynomial
, as a nonreal root of the polynomial
with rational coefficients, will be a quadratic number.
For algebraic numbers $s$![]() of degree $d=4$
of degree $d=4$![]() we will show that the sumset of at most four sets is everywhere dense in ${\mathbb {C}}$
we will show that the sumset of at most four sets is everywhere dense in ${\mathbb {C}}$![]() and that three sets are not sufficient for exceptional numbers $s$
and that three sets are not sufficient for exceptional numbers $s$![]() .
.
Theorem 1.5 If $s \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() is a quartic algebraic number, which is not exceptional, then there exist $n, m \in {\mathbb {N}}$
is a quartic algebraic number, which is not exceptional, then there exist $n, m \in {\mathbb {N}}$![]() such that the sumset (1.3) is everywhere dense in ${\mathbb {C}}$
such that the sumset (1.3) is everywhere dense in ${\mathbb {C}}$![]() for $t=ms+s^2$
for $t=ms+s^2$![]() .
.
On the other hand, if a quartic algebraic number $s \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() is exceptional, then for any $s_1, s_2, s_3 \in {\mathbb {N}}[s]$
is exceptional, then for any $s_1, s_2, s_3 \in {\mathbb {N}}[s]$![]() the sumset
the sumset
is not dense in ${\mathbb {C}}$![]() , but there are $t_1, t_2, t_3, t_4 \in {\mathbb {N}}[s]$
, but there are $t_1, t_2, t_3, t_4 \in {\mathbb {N}}[s]$![]() for which the sumset
for which the sumset
is everywhere dense in ${\mathbb {C}}$![]() .
.
Recall that no sumset of the form (1.4) is dense in ${\mathbb {C}}$![]() for a quadratic algebraic number $s$
for a quadratic algebraic number $s$![]() and $s_1, \dots, s_k \in {\mathbb {N}}[s]$
and $s_1, \dots, s_k \in {\mathbb {N}}[s]$![]() . Therefore, for such $s$
. Therefore, for such $s$![]() the set ${\mathbb {N}}[s]$
the set ${\mathbb {N}}[s]$![]() does not contain a finitely generated semigroup $A$
does not contain a finitely generated semigroup $A$![]() that is dense in ${\mathbb {C}}$
that is dense in ${\mathbb {C}}$![]() (although, by theorem 1.4, ${\mathbb {N}}[s]$
(although, by theorem 1.4, ${\mathbb {N}}[s]$![]() itself is dense in ${\mathbb {C}}$
itself is dense in ${\mathbb {C}}$![]() if $s$
if $s$![]() is not a quadratic algebraic integer). The situation is different for other $s \in {\mathbb {C}} \setminus {\mathbb {R}}$
is not a quadratic algebraic integer). The situation is different for other $s \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() . For each of those $s$
. For each of those $s$![]() , by theorems 1.3 and 1.5, such a semigroup $A \subset {\mathbb {N}}[s]$
, by theorems 1.3 and 1.5, such a semigroup $A \subset {\mathbb {N}}[s]$![]() exists. Moreover, these theorems also determine the smallest possible rank of a semigroup $A$
exists. Moreover, these theorems also determine the smallest possible rank of a semigroup $A$![]() in ${\mathbb {N}}[s]$
in ${\mathbb {N}}[s]$![]() that is everywhere dense in ${\mathbb {C}}$
that is everywhere dense in ${\mathbb {C}}$![]() :
:
Corollary 1.6 For $s \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() the set ${\mathbb {N}}[s]$
the set ${\mathbb {N}}[s]$![]() contains a finitely generated additive semigroup $A$
contains a finitely generated additive semigroup $A$![]() that is everywhere dense in ${\mathbb {C}}$
that is everywhere dense in ${\mathbb {C}}$![]() if and only if $s$
if and only if $s$![]() is a transcendental number or an algebraic number of degree $d>2$
is a transcendental number or an algebraic number of degree $d>2$![]() . The smallest possible rank of such a semigroup $A \subset {\mathbb {N}}[s]$
. The smallest possible rank of such a semigroup $A \subset {\mathbb {N}}[s]$![]() equals $3$
equals $3$![]() , unless $s$
, unless $s$![]() is an exceptional number in which case the smallest possible rank of such $A$
is an exceptional number in which case the smallest possible rank of such $A$![]() equals $4$
equals $4$![]() .
.
Note that $t$![]() in theorem 1.3 is either $s$
in theorem 1.3 is either $s$![]() or a quadratic polynomial in $s$
or a quadratic polynomial in $s$![]() . Also, the power $n$
. Also, the power $n$![]() will be chosen in lemma 4.3: it depends on $t, s$
will be chosen in lemma 4.3: it depends on $t, s$![]() , and so on $s$
, and so on $s$![]() only. The same numbers $t, n$
only. The same numbers $t, n$![]() also appear in the first part of theorem 1.5. Furthermore, $t_1, t_2, t_3, t_4$
also appear in the first part of theorem 1.5. Furthermore, $t_1, t_2, t_3, t_4$![]() in the last part of theorem 1.5 are polynomials in $s$
in the last part of theorem 1.5 are polynomials in $s$![]() whose degrees depend on $s$
whose degrees depend on $s$![]() only (see (7.6) and the proof later on). Therefore, theorems 1.3 and 1.5 also imply the following approximation result for polynomials with nonnegative coefficients:
only (see (7.6) and the proof later on). Therefore, theorems 1.3 and 1.5 also imply the following approximation result for polynomials with nonnegative coefficients:
Corollary 1.7 Let $s \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() be a transcendental number or an algebraic number of degree $d>2$
be a transcendental number or an algebraic number of degree $d>2$![]() . Then, there is a positive integer $n=n(s)$
. Then, there is a positive integer $n=n(s)$![]() , which depends only on $s$
, which depends only on $s$![]() , such that for any $z \in {\mathbb {C}}$
, such that for any $z \in {\mathbb {C}}$![]() and any $\varepsilon >0$
and any $\varepsilon >0$![]() there exist $a_1, \dots, a_n \in {\mathbb {N}}_0$
there exist $a_1, \dots, a_n \in {\mathbb {N}}_0$![]() , not all zeros, for which
, not all zeros, for which
For most $s$![]() corollary 1.7 is stronger than theorem 1.2, because in (1.8) the degree of approximating polynomial is bounded by a constant depending on $s$
corollary 1.7 is stronger than theorem 1.2, because in (1.8) the degree of approximating polynomial is bounded by a constant depending on $s$![]() only. For the algebraic number $s$
only. For the algebraic number $s$![]() of degree $d=2$
of degree $d=2$![]() , which is not an algebraic integer, the inequality (1.8) also holds by theorem 1.4. However, in that case, as the sumset (1.4) is not dense in ${\mathbb {C}}$
, which is not an algebraic integer, the inequality (1.8) also holds by theorem 1.4. However, in that case, as the sumset (1.4) is not dense in ${\mathbb {C}}$![]() for any fixed $s_1, \dots, s_k \in {\mathbb {N}}[s]$
for any fixed $s_1, \dots, s_k \in {\mathbb {N}}[s]$![]() , the integer $n$
, the integer $n$![]() in (1.8) depends not only on $s$
in (1.8) depends not only on $s$![]() . (In principle, it depends on $s, z$
. (In principle, it depends on $s, z$![]() and $\varepsilon$
and $\varepsilon$![]() .)
.)
In corollary 1.7, the degree $n$![]() is fixed, while the coefficients $a_i \in {\mathbb {N}}_0$
is fixed, while the coefficients $a_i \in {\mathbb {N}}_0$![]() are allowed to grow. In [Reference Feng13] and similar papers, the coefficients $a_i$
are allowed to grow. In [Reference Feng13] and similar papers, the coefficients $a_i$![]() all belong to a finite set, while the degree $n$
all belong to a finite set, while the degree $n$![]() is allowed to grow. Specifically, for $s>1$
is allowed to grow. Specifically, for $s>1$![]() the density in ${\mathbb {R}}$
the density in ${\mathbb {R}}$![]() of the polynomials $\sum _{i=0}^n a_i s^i$
of the polynomials $\sum _{i=0}^n a_i s^i$![]() with coefficients $a_i \in {\mathbb {Z}} \cap [-m, m]$
with coefficients $a_i \in {\mathbb {Z}} \cap [-m, m]$![]() has been established for every $s \in (1, m+1)$
has been established for every $s \in (1, m+1)$![]() which is not a Pisot number. In our earlier paper [Reference Dubickas10], where the density in ${\mathbb {R}}$
which is not a Pisot number. In our earlier paper [Reference Dubickas10], where the density in ${\mathbb {R}}$![]() has been investigated, the coefficients were allowed to take values in ${\mathbb {N}}$
has been investigated, the coefficients were allowed to take values in ${\mathbb {N}}$![]() and there was no restriction on the degree, so no condition related to Pisot numbers appears in theorem 1.1.
and there was no restriction on the degree, so no condition related to Pisot numbers appears in theorem 1.1.
Our approach to the proof of theorem 1.3 rests on the following recent result [Reference Dubickas11] (whose motivation came from [Reference Konyagin, Sha, Shparlinski and Stewart17]).
Theorem 1.8 For $\alpha, \beta, \gamma \in {\mathbb {C}}$![]() the set
the set
is everywhere dense in ${\mathbb {C}}$![]() if and only if the imaginary parts
if and only if the imaginary parts
are linearly independent over ${\mathbb {Q}}$![]() .
.
Unfortunately, we cannot use theorem 1.8 as stated, because we are working not with the sumset ${\mathbb {Z}} \alpha +{\mathbb {Z}} \beta +{\mathbb {Z}} \gamma$![]() , which is an additive group, but with the additive semigroup ${\mathbb {N}} \alpha +{\mathbb {N}} \beta +{\mathbb {N}} \gamma$
, which is an additive group, but with the additive semigroup ${\mathbb {N}} \alpha +{\mathbb {N}} \beta +{\mathbb {N}} \gamma$![]() , which can be smaller. For this purpose, we will establish the following analogue of theorem 1.8:
, which can be smaller. For this purpose, we will establish the following analogue of theorem 1.8:
Theorem 1.9 For $\alpha, \beta, \gamma \in {\mathbb {C}}$![]() the set
the set
is everywhere dense in ${\mathbb {C}}$![]() if and only if the imaginary parts
if and only if the imaginary parts
are linearly independent over ${\mathbb {Q}}$![]() and the point $z=0$
and the point $z=0$![]() belongs to the interior of a triangle with vertices at $\alpha, \beta, \gamma$
belongs to the interior of a triangle with vertices at $\alpha, \beta, \gamma$![]() .
.
In the next section we will prove theorem 1.4. Section 3 is devoted to the proof of theorem 1.9. Then, in § 4 we will prove five auxiliary lemmas of different types. In § 5, using theorem 1.9 and one of the lemmas, we will prove a proposition describing the conditions on $t$![]() under which the sumset (1.3) is everywhere dense in ${\mathbb {C}}$
under which the sumset (1.3) is everywhere dense in ${\mathbb {C}}$![]() . Finally, in § 6 and 7, combining this proposition with some previous lemmas, we will complete the proofs of theorems 1.3 and 1.5. It is clear that theorems 1.3, 1.4, 1.5 combined with the explanation of the necessity of the conditions $s \notin {\mathbb {R}}$
. Finally, in § 6 and 7, combining this proposition with some previous lemmas, we will complete the proofs of theorems 1.3 and 1.5. It is clear that theorems 1.3, 1.4, 1.5 combined with the explanation of the necessity of the conditions $s \notin {\mathbb {R}}$![]() and $s$
and $s$![]() is not a quadratic algebraic integer imply theorem 1.2.
is not a quadratic algebraic integer imply theorem 1.2.
2. The set ${\mathbb {N}}[s]$ for algebraic $s$
for algebraic $s$ without positive conjugates
without positive conjugates
In this section we assume that $s \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() is an algebraic number which is not a quadratic algebraic integer and has no conjugates in $(0, \infty )$
is an algebraic number which is not a quadratic algebraic integer and has no conjugates in $(0, \infty )$![]() . We will show how the desired result about the density of ${\mathbb {N}}[s]$
. We will show how the desired result about the density of ${\mathbb {N}}[s]$![]() in ${\mathbb {C}}$
in ${\mathbb {C}}$![]() can be easily derived from the above-mentioned result [24] about the density of ${\mathbb {Z}}[s]$
can be easily derived from the above-mentioned result [24] about the density of ${\mathbb {Z}}[s]$![]() in ${\mathbb {C}}$
in ${\mathbb {C}}$![]() .
.
Assume that an algebraic number $s \ne 0$![]() has no conjugates in $(0, \infty )$
has no conjugates in $(0, \infty )$![]() (including $s$
(including $s$![]() itself). Then, $s$
itself). Then, $s$![]() is a root of some nonzero polynomial with nonnegative integer coefficients. (This result is essentially due to Meissner [Reference Meissner19]. It was also proved in [Reference Akiyama3], [Reference Brunotte4], [Reference Correa-Morris and Gotti6], [Reference Curtiss7], [Reference Dubickas9], [Reference Handelman15].) Hence,
is a root of some nonzero polynomial with nonnegative integer coefficients. (This result is essentially due to Meissner [Reference Meissner19]. It was also proved in [Reference Akiyama3], [Reference Brunotte4], [Reference Correa-Morris and Gotti6], [Reference Curtiss7], [Reference Dubickas9], [Reference Handelman15].) Hence,

for some $m, a_0, a_m \in {\mathbb {N}}$![]() and $a_1, \dots, a_{m-1} \in {\mathbb {N}}_0$
and $a_1, \dots, a_{m-1} \in {\mathbb {N}}_0$![]() . This, by the definition of ${\mathbb {N}}[s]$
. This, by the definition of ${\mathbb {N}}[s]$![]() in (1.1), yields
in (1.1), yields

Consequently,
by the additivity of ${\mathbb {N}}[s]$![]() and $a_0^2=(-a_0)^2 \in {\mathbb {N}}[s]$
and $a_0^2=(-a_0)^2 \in {\mathbb {N}}[s]$![]() by its multiplicativity. This implies $\pm a_0^2 s^j \in {\mathbb {N}}[s]$
by its multiplicativity. This implies $\pm a_0^2 s^j \in {\mathbb {N}}[s]$![]() for every $j \in {\mathbb {N}}_0$
for every $j \in {\mathbb {N}}_0$![]() . Thus, selecting $a=a_0^2 \in {\mathbb {N}}$
. Thus, selecting $a=a_0^2 \in {\mathbb {N}}$![]() we get the following:
we get the following:
Lemma 2.1 If $s \ne 0$![]() is an algebraic number whose conjugates over ${\mathbb {Q}}$
is an algebraic number whose conjugates over ${\mathbb {Q}}$![]() (including $s$
(including $s$![]() itself) do not belong to the interval $(0, \infty )$
itself) do not belong to the interval $(0, \infty )$![]() , then there is a positive integer $a$
, then there is a positive integer $a$![]() which depends on $s$
which depends on $s$![]() only such that
only such that
By [24], we know that, if $s \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() is an algebraic number that is not a quadratic algebraic integer, then ${\mathbb {Z}}[s]$
is an algebraic number that is not a quadratic algebraic integer, then ${\mathbb {Z}}[s]$![]() is everywhere dense in ${\mathbb {C}}$
is everywhere dense in ${\mathbb {C}}$![]() . This, combined with lemma 2.1, implies the following:
. This, combined with lemma 2.1, implies the following:
Corollary 2.2 If $s \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() is an algebraic number which is not a quadratic algebraic integer and has no conjugates in $(0, \infty )$
is an algebraic number which is not a quadratic algebraic integer and has no conjugates in $(0, \infty )$![]() , then the set ${\mathbb {N}}[s]$
, then the set ${\mathbb {N}}[s]$![]() is everywhere dense in ${\mathbb {C}}$
is everywhere dense in ${\mathbb {C}}$![]() .
.
In particular, if $s \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() is quadratic then it has no real conjugates, since its only conjugate over ${\mathbb {Q}}$
is quadratic then it has no real conjugates, since its only conjugate over ${\mathbb {Q}}$![]() , which is not equal to $s$
, which is not equal to $s$![]() , must be its complex conjugate $\overline {s} \notin {\mathbb {R}}$
, must be its complex conjugate $\overline {s} \notin {\mathbb {R}}$![]() . Hence, corollary 2.2 implies theorem 1.4.
. Hence, corollary 2.2 implies theorem 1.4.
3. Proof of theorem 1.9
In the proof of theorem 1.9 we shall use Kronecker's approximation theorem; see, for instance, [Reference Aggarwal and Singh1, Theorem 9], [Reference Gonek and Montgomery14, p. 507], [Reference Kueh18].
Lemma 3.1 Let $\lambda _1, \dots, \lambda _N$![]() be real numbers such that $1, \lambda _1, \dots, \lambda _N$
be real numbers such that $1, \lambda _1, \dots, \lambda _N$![]() are linearly independent over ${\mathbb {Q}}$
are linearly independent over ${\mathbb {Q}}$![]() , and let $\omega _1, \omega _2, \dots, \omega _N$
, and let $\omega _1, \omega _2, \dots, \omega _N$![]() be arbitrary real numbers. Then, for any $\epsilon >0$
be arbitrary real numbers. Then, for any $\epsilon >0$![]() , there exist $T \in {\mathbb {N}}$
, there exist $T \in {\mathbb {N}}$![]() and $T_1, \dots, T_N \in {\mathbb {Z}}$
and $T_1, \dots, T_N \in {\mathbb {Z}}$![]() such that
such that
for $n=1, 2, \dots, N$![]() .
.
If the point $z=0$![]() does not belong to the interior of a triangle with vertices at $\alpha, \beta, \gamma \in {\mathbb {C}}$
does not belong to the interior of a triangle with vertices at $\alpha, \beta, \gamma \in {\mathbb {C}}$![]() , then there is a line $L$
, then there is a line $L$![]() through the point $z=0$
through the point $z=0$![]() such that the points $\alpha, \beta, \gamma$
such that the points $\alpha, \beta, \gamma$![]() all belong to the same side of the line $L$
all belong to the same side of the line $L$![]() (possibly including the line $L$
(possibly including the line $L$![]() itself). Then, all the points of the sumset ${\mathbb {N}}\alpha +{\mathbb {N}} \beta +{\mathbb {N}}\gamma$
itself). Then, all the points of the sumset ${\mathbb {N}}\alpha +{\mathbb {N}} \beta +{\mathbb {N}}\gamma$![]() are also on the same side of $L$
are also on the same side of $L$![]() (including $L$
(including $L$![]() itself). Consequently, this sumset is not dense in ${\mathbb {C}}$
itself). Consequently, this sumset is not dense in ${\mathbb {C}}$![]() . Also, if the imaginary parts $\Im (\alpha \overline {\beta }), \Im (\beta \overline {\gamma }), \Im (\gamma \overline {\alpha })$
. Also, if the imaginary parts $\Im (\alpha \overline {\beta }), \Im (\beta \overline {\gamma }), \Im (\gamma \overline {\alpha })$![]() are linearly dependent over ${\mathbb {Q}}$
are linearly dependent over ${\mathbb {Q}}$![]() , then the sumset ${\mathbb {Z}}\alpha +{\mathbb {Z}}\beta +{\mathbb {Z}}\gamma$
, then the sumset ${\mathbb {Z}}\alpha +{\mathbb {Z}}\beta +{\mathbb {Z}}\gamma$![]() is not dense in ${\mathbb {C}}$
is not dense in ${\mathbb {C}}$![]() by theorem 1.8. Therefore, ${\mathbb {N}}\alpha +{\mathbb {N}}\beta +{\mathbb {N}}\gamma$
by theorem 1.8. Therefore, ${\mathbb {N}}\alpha +{\mathbb {N}}\beta +{\mathbb {N}}\gamma$![]() , as a subset of ${\mathbb {Z}}\alpha +{\mathbb {Z}}\beta +{\mathbb {Z}}\gamma$
, as a subset of ${\mathbb {Z}}\alpha +{\mathbb {Z}}\beta +{\mathbb {Z}}\gamma$![]() , cannot be dense in ${\mathbb {C}}$
, cannot be dense in ${\mathbb {C}}$![]() either.
either.
From now on we assume that the point $z=0$![]() belongs to the interior of the triangle with vertices at $\alpha, \beta, \gamma$
belongs to the interior of the triangle with vertices at $\alpha, \beta, \gamma$![]() and that the three numbers $\Im (\alpha \overline {\beta }), \Im (\beta \overline {\gamma }), \Im (\gamma \overline {\alpha })$
and that the three numbers $\Im (\alpha \overline {\beta }), \Im (\beta \overline {\gamma }), \Im (\gamma \overline {\alpha })$![]() are linearly independent over ${\mathbb {Q}}$
are linearly independent over ${\mathbb {Q}}$![]() . In order to complete the proof of theorem 1.9 it remains to show that the sumset ${\mathbb {N}}\alpha +{\mathbb {N}} \beta +{\mathbb {N}}\gamma$
. In order to complete the proof of theorem 1.9 it remains to show that the sumset ${\mathbb {N}}\alpha +{\mathbb {N}} \beta +{\mathbb {N}}\gamma$![]() is everywhere dense in ${\mathbb {C}}$
is everywhere dense in ${\mathbb {C}}$![]() .
.
Of course, the linear independence of the above imaginary parts implies that $\alpha, \beta, \gamma \ne 0$![]() . Note that by multiplying all three numbers $\alpha, \beta, \gamma$
. Note that by multiplying all three numbers $\alpha, \beta, \gamma$![]() by the same number $\gamma ^{-1}$
by the same number $\gamma ^{-1}$![]() we do not change any of the two conditions. The point $z=0$
we do not change any of the two conditions. The point $z=0$![]() still belongs to the interior of a triangle with vertices at $\alpha, \beta, 1$
still belongs to the interior of a triangle with vertices at $\alpha, \beta, 1$![]() (where we use the notation $\alpha$
(where we use the notation $\alpha$![]() for $\alpha \gamma ^{-1}$
for $\alpha \gamma ^{-1}$![]() and $\beta$
and $\beta$![]() for $\beta \gamma ^{-1}$
for $\beta \gamma ^{-1}$![]() ) and the three numbers $\Im (\alpha \overline {\beta }), \Im (\beta ), \Im (\overline {\alpha })$
) and the three numbers $\Im (\alpha \overline {\beta }), \Im (\beta ), \Im (\overline {\alpha })$![]() are still linearly independent over ${\mathbb {Q}}$
are still linearly independent over ${\mathbb {Q}}$![]() . We will show that the sumset ${\mathbb {N}}+{\mathbb {N}} \alpha +{\mathbb {N}}\beta$
. We will show that the sumset ${\mathbb {N}}+{\mathbb {N}} \alpha +{\mathbb {N}}\beta$![]() is everywhere dense in ${\mathbb {C}}$
is everywhere dense in ${\mathbb {C}}$![]() .
.
Set
where $u, v, w, l \in {\mathbb {R}}$![]() . Since the point $z=0$
. Since the point $z=0$![]() lies in the interior of the triangle with vertices at $\alpha, \beta, 1$
lies in the interior of the triangle with vertices at $\alpha, \beta, 1$![]() , the numbers $v, l$
, the numbers $v, l$![]() must be either both positive or both negative. Without the restriction of generality (by swapping $\alpha$
must be either both positive or both negative. Without the restriction of generality (by swapping $\alpha$![]() and $\beta$
and $\beta$![]() if necessary) we can assume that $v, l>0$
if necessary) we can assume that $v, l>0$![]() . Furthermore, at least one of the numbers $u, -w$
. Furthermore, at least one of the numbers $u, -w$![]() must be negative, since otherwise $z=0$
must be negative, since otherwise $z=0$![]() does not lie in the interior of the triangle $\alpha, \beta, 1$
does not lie in the interior of the triangle $\alpha, \beta, 1$![]() . Again, by swapping $\alpha, \beta$
. Again, by swapping $\alpha, \beta$![]() by $\overline {\beta }, \overline {\alpha }$
by $\overline {\beta }, \overline {\alpha }$![]() if necessary, we can assume that the number $-w$
if necessary, we can assume that the number $-w$![]() is negative, i.e. $w>0$
is negative, i.e. $w>0$![]() . Therefore, without loss of generality, we can assume that $v, w, l>0$
. Therefore, without loss of generality, we can assume that $v, w, l>0$![]() . The sign of $u$
. The sign of $u$![]() can be arbitrary (it is also possible that $u=0$
can be arbitrary (it is also possible that $u=0$![]() ), but the argument of the complex number $\alpha$
), but the argument of the complex number $\alpha$![]() plus $\pi$
plus $\pi$![]() must be greater than the argument of $\beta$
must be greater than the argument of $\beta$![]() . (The argument $\arg z$
. (The argument $\arg z$![]() of a complex number $z \ne 0$
of a complex number $z \ne 0$![]() is a unique real number in the interval $[0, 2\pi )$
is a unique real number in the interval $[0, 2\pi )$![]() for which $z=|z| e^{i \arg z}$
for which $z=|z| e^{i \arg z}$![]() .)
.)
Let $\theta _1, \theta _2 \in (0, 2\pi )$![]() be the arguments of $\alpha$
be the arguments of $\alpha$![]() and $\beta$
and $\beta$![]() , respectively. Then, $\theta _1 \in (0, \pi )$
, respectively. Then, $\theta _1 \in (0, \pi )$![]() and $\theta _2 \in (\pi, {3\pi }/{2})$
and $\theta _2 \in (\pi, {3\pi }/{2})$![]() . The condition $\theta _1+\pi >\theta _2$
. The condition $\theta _1+\pi >\theta _2$![]() automatically holds if $u \leq 0$
automatically holds if $u \leq 0$![]() . In the case when $u>0$
. In the case when $u>0$![]() the condition $\theta _1+\pi >\theta _2$
the condition $\theta _1+\pi >\theta _2$![]() is equivalent to $\tan (\theta _1)>\tan (\theta _2)$
is equivalent to $\tan (\theta _1)>\tan (\theta _2)$![]() , namely, $v/u>l/w$
, namely, $v/u>l/w$![]() . Hence,
. Hence,
Of course, by $v, w, l>0$![]() , the inequality (3.2) trivially holds for $u \leq 0$
, the inequality (3.2) trivially holds for $u \leq 0$![]() . So, from now on we will assume that $v, w, l>0$
. So, from now on we will assume that $v, w, l>0$![]() and $u \in {\mathbb {R}}$
and $u \in {\mathbb {R}}$![]() satisfy (3.2).
satisfy (3.2).
We know that the numbers $\Im (\alpha \overline {\beta })=ul-vw$![]() , $\Im (\beta )=-l$
, $\Im (\beta )=-l$![]() , $\Im (\overline {\alpha })=-v$
, $\Im (\overline {\alpha })=-v$![]() are linearly independent over ${\mathbb {Q}}$
are linearly independent over ${\mathbb {Q}}$![]() . Dividing by $-l$
. Dividing by $-l$![]() we deduce that the numbers
we deduce that the numbers
are linearly independent over ${\mathbb {Q}}$![]() too.
too.
Now, the conclusion of the proof is essentially the same as that in [Reference Dubickas11]. Fix two arbitrary real numbers $X$![]() and $Y$
and $Y$![]() . We need to show that, for any positive number $\varepsilon$
. We need to show that, for any positive number $\varepsilon$![]() , there exist $a, b, c \in {\mathbb {N}}$
, there exist $a, b, c \in {\mathbb {N}}$![]() for which the sum $a+b\alpha +c\beta$
for which the sum $a+b\alpha +c\beta$![]() is close to $X+iY$
is close to $X+iY$![]() , namely,
, namely,
Set
By lemma 3.1 applied to $\lambda _1=v/l$![]() , $\lambda _2=vw/l-u$
, $\lambda _2=vw/l-u$![]() and $\omega _1, \omega _2$
and $\omega _1, \omega _2$![]() as defined in (3.4), for any $\epsilon >0$
as defined in (3.4), for any $\epsilon >0$![]() , there exist $b \in {\mathbb {N}}$
, there exist $b \in {\mathbb {N}}$![]() and $a, c \in {\mathbb {Z}}$
and $a, c \in {\mathbb {Z}}$![]() such that
such that
Since the numbers $v/l$![]() and $vw/l-u$
and $vw/l-u$![]() are irrational (as they both and $1$
are irrational (as they both and $1$![]() are linearly independent over ${\mathbb {Q}}$
are linearly independent over ${\mathbb {Q}}$![]() ), the above inequalities have infinitely many solutions in $b \in {\mathbb {N}}$
), the above inequalities have infinitely many solutions in $b \in {\mathbb {N}}$![]() . For $b$
. For $b$![]() sufficiently large we must have $c \in {\mathbb {N}}$
sufficiently large we must have $c \in {\mathbb {N}}$![]() and $a \in {\mathbb {N}}$
and $a \in {\mathbb {N}}$![]() due to $v/l>0$
due to $v/l>0$![]() and (3.2). Hence, we can assume that $a, b, c \in {\mathbb {N}}$
and (3.2). Hence, we can assume that $a, b, c \in {\mathbb {N}}$![]() .
.
Next, in view of (3.4), by multiplying the first inequality by $l>0$![]() , we get
, we get
Similarly, by (3.4), multiplying the second inequality by $l>0$![]() we deduce
we deduce
This inequality can be written in the equivalent form
Now, by the triangle inequality, $w>0$![]() and (3.5), it follows that
and (3.5), it follows that
and hence
It is clear that (3.5) and (3.6) imply (3.3) provided that $\epsilon$![]() is satisfies
is satisfies
This completes the proof of the theorem.
4. Auxiliary lemmas
We begin with the following lemma, which will be used in the proof of proposition 5.1 later on.
Lemma 4.1 Assume that $s$![]() is a transcendental nonreal number. Then, for at least one number $t \in \{s, s+s^2\}$
is a transcendental nonreal number. Then, for at least one number $t \in \{s, s+s^2\}$![]() all three numbers $t, |t|, t/|t|$
all three numbers $t, |t|, t/|t|$![]() are transcendental.
are transcendental.
Proof. Write $s=\varrho e^{i \alpha }$![]() , with $\varrho >0$
, with $\varrho >0$![]() and argument $\alpha \in (0, \pi ) \cup (\pi, 2\pi )$
and argument $\alpha \in (0, \pi ) \cup (\pi, 2\pi )$![]() . If the numbers $s$
. If the numbers $s$![]() , $|s|=\varrho$
, $|s|=\varrho$![]() and $s/|s|=e^{i \alpha }$
and $s/|s|=e^{i \alpha }$![]() are all three transcendental, then the assertion of the lemma holds with $t=s$
are all three transcendental, then the assertion of the lemma holds with $t=s$![]() . If not, then either $e^{i\alpha }$
. If not, then either $e^{i\alpha }$![]() or $\varrho$
or $\varrho$![]() is algebraic. (They cannot be both algebraic by the assumption of the lemma on $s$
is algebraic. (They cannot be both algebraic by the assumption of the lemma on $s$![]() .) We will show that then the assertion of the lemma holds for number $t=s+s^2$
.) We will show that then the assertion of the lemma holds for number $t=s+s^2$![]() . Set $t=|t| e^{i\beta }$
. Set $t=|t| e^{i\beta }$![]() , where $0 \leq \beta <2\pi$
, where $0 \leq \beta <2\pi$![]() .
.
From
we find that
and
Assume first that $e^{i\alpha }=\cos (\alpha )+i\sin (\alpha )$![]() is algebraic and $\varrho$
is algebraic and $\varrho$![]() is transcendental. Then, $\cos (\alpha )={e^{i\alpha }+e^{-i\alpha }}/{2}$
is transcendental. Then, $\cos (\alpha )={e^{i\alpha }+e^{-i\alpha }}/{2}$![]() and $\sin (\alpha )={e^{i\alpha }-e^{-i\alpha }}/{2i}$
and $\sin (\alpha )={e^{i\alpha }-e^{-i\alpha }}/{2i}$![]() are both algebraic. If $|t|$
are both algebraic. If $|t|$![]() were algebraic, then, as $|t|^2$
were algebraic, then, as $|t|^2$![]() and $\cos (\alpha )$
and $\cos (\alpha )$![]() are both algebraic, $\varrho$
are both algebraic, $\varrho$![]() were algebraic by (4.1), a contradiction. Hence, $|t|$
were algebraic by (4.1), a contradiction. Hence, $|t|$![]() is transcendental. Assume that $t/|t|=e^{i\beta }$
is transcendental. Assume that $t/|t|=e^{i\beta }$![]() is algebraic. If $\beta \in \{{\pi }/{2}, {3\pi }/{2}\}$
is algebraic. If $\beta \in \{{\pi }/{2}, {3\pi }/{2}\}$![]() , then $\Re (t)=0$
, then $\Re (t)=0$![]() . Hence, $\varrho \cos (\alpha )+\varrho ^2 \cos (2\alpha )=0$
. Hence, $\varrho \cos (\alpha )+\varrho ^2 \cos (2\alpha )=0$![]() , and so $\cos (\alpha )+\varrho \cos (2\alpha )=0$
, and so $\cos (\alpha )+\varrho \cos (2\alpha )=0$![]() . This is not the case, because $\varrho \notin \overline {{\mathbb {Q}}}$
. This is not the case, because $\varrho \notin \overline {{\mathbb {Q}}}$![]() (where $\overline {{\mathbb {Q}}}$
(where $\overline {{\mathbb {Q}}}$![]() stands for the set of algebraic numbers) and $\cos (\alpha ), \cos (2\alpha )=2\cos ^2(\alpha )-1 \in \overline {{\mathbb {Q}}}$
stands for the set of algebraic numbers) and $\cos (\alpha ), \cos (2\alpha )=2\cos ^2(\alpha )-1 \in \overline {{\mathbb {Q}}}$![]() cannot be both zeros. It follows that $\tan (\beta )$
cannot be both zeros. It follows that $\tan (\beta )$![]() in (4.2) is well defined, namely, $\beta \notin \{{\pi }/{2}, {3\pi }/{2}\}$
in (4.2) is well defined, namely, $\beta \notin \{{\pi }/{2}, {3\pi }/{2}\}$![]() .
.
Since $\tan (\beta ), \cos (\alpha ), \cos (2\alpha ), \sin (\alpha ), \sin (2\alpha ) \in \overline {{\mathbb {Q}}}$![]() and $\varrho \notin \overline {{\mathbb {Q}}}$
and $\varrho \notin \overline {{\mathbb {Q}}}$![]() , equality in (4.2) holds only if
, equality in (4.2) holds only if
We know that $\sin (\alpha ) \ne 0$![]() , so $\cos (\alpha ) \ne 0$
, so $\cos (\alpha ) \ne 0$![]() by the first equality in (4.3). Thus, $\sin (2\alpha ) \ne 0$
by the first equality in (4.3). Thus, $\sin (2\alpha ) \ne 0$![]() . Hence, by (4.3), we obtain $\tan (\beta ) \ne 0$
. Hence, by (4.3), we obtain $\tan (\beta ) \ne 0$![]() and
and
which implies
which is absurd. This proves that $e^{i\beta }=t/|t|$![]() is transcendental.
is transcendental.
Now, assume that $\varrho$![]() is algebraic and $e^{i\alpha }$
is algebraic and $e^{i\alpha }$![]() is transcendental. Then, $\cos (\alpha )$
is transcendental. Then, $\cos (\alpha )$![]() must be transcendental too. From (4.1) we see that that $|t|^2$
must be transcendental too. From (4.1) we see that that $|t|^2$![]() is transcendental, and hence so is $|t|$
is transcendental, and hence so is $|t|$![]() . It remains to prove that $e^{i\beta }$
. It remains to prove that $e^{i\beta }$![]() is transcendental. Assume that $e^{i\beta } \in \overline {{\mathbb {Q}}}$
is transcendental. Assume that $e^{i\beta } \in \overline {{\mathbb {Q}}}$![]() . It is clear that then $\tan (\beta ) \in \overline {{\mathbb {Q}}}$
. It is clear that then $\tan (\beta ) \in \overline {{\mathbb {Q}}}$![]() or $\beta \in \{{\pi }/{2}, {3\pi }/{2}\}$
or $\beta \in \{{\pi }/{2}, {3\pi }/{2}\}$![]() . However, if $\beta \in \{{\pi }/{2}, {3\pi }/{2}\}$
. However, if $\beta \in \{{\pi }/{2}, {3\pi }/{2}\}$![]() , then $\Re (t)=0$
, then $\Re (t)=0$![]() , which means that $\cos (\alpha )+\varrho \cos (2\alpha )=0$
, which means that $\cos (\alpha )+\varrho \cos (2\alpha )=0$![]() . Then, $x=\cos (\alpha )$
. Then, $x=\cos (\alpha )$![]() is a root of the nonzero polynomial with algebraic coefficients $2\varrho x^2+x-\varrho$
is a root of the nonzero polynomial with algebraic coefficients $2\varrho x^2+x-\varrho$![]() . Hence, $\cos (\alpha ) \in \overline {{\mathbb {Q}}}$
. Hence, $\cos (\alpha ) \in \overline {{\mathbb {Q}}}$![]() , a contradiction. Therefore, $\tan (\beta )$
, a contradiction. Therefore, $\tan (\beta )$![]() in (4.2) is well defined. Squaring both sides of (4.2) we obtain
in (4.2) is well defined. Squaring both sides of (4.2) we obtain
where $x=\cos (\alpha )$![]() . Since $x$
. Since $x$![]() is transcendental and $\varrho, \tan (\beta ) \in \overline {{\mathbb {Q}}}$
is transcendental and $\varrho, \tan (\beta ) \in \overline {{\mathbb {Q}}}$![]() , equality holds only if the resulting quartic polynomials on both sides are identical. However, their coefficients for $x^4$
, equality holds only if the resulting quartic polynomials on both sides are identical. However, their coefficients for $x^4$![]() are $4\varrho ^2 \tan ^2(\beta )$
are $4\varrho ^2 \tan ^2(\beta )$![]() and $-4\varrho ^2$
and $-4\varrho ^2$![]() . Since $\varrho > 0$
. Since $\varrho > 0$![]() , they are equal only in the case when $\tan ^2(\beta )=-1$
, they are equal only in the case when $\tan ^2(\beta )=-1$![]() , which is impossible. This completes the proof of the lemma.
, which is impossible. This completes the proof of the lemma.
The next lemma is similar to lemma 4.1, but deals with algebraic $s$![]() rather than transcendental.
rather than transcendental.
Lemma 4.2 For each algebraic nonreal number $s$![]() there is $m_0 \in {\mathbb {N}}$
there is $m_0 \in {\mathbb {N}}$![]() such that for each integer $m \geq m_0$
such that for each integer $m \geq m_0$![]() the argument $\beta _m$
the argument $\beta _m$![]() of the number $ms+s^2$
of the number $ms+s^2$![]() satisfies ${\beta _m}/{\pi } \notin {\mathbb {Q}}$
satisfies ${\beta _m}/{\pi } \notin {\mathbb {Q}}$![]() .
.
Proof. Assume that $s=\varrho e^{i \alpha }$![]() . Set $t_m=ms+s^2=|t_m| e^{i\beta _m}$
. Set $t_m=ms+s^2=|t_m| e^{i\beta _m}$![]() . Then, as in (4.2), we find that
. Then, as in (4.2), we find that
Since $\sin (\alpha ) \ne 0$![]() and $m+2\varrho \cos (\alpha ) \ne 0$
and $m+2\varrho \cos (\alpha ) \ne 0$![]() for $m$
for $m$![]() sufficiently large, the right hand side of (4.4) is nonzero. Also, in case $\cos (\alpha )=0$
sufficiently large, the right hand side of (4.4) is nonzero. Also, in case $\cos (\alpha )=0$![]() we have $m\cos (\alpha )+\varrho \cos (2\alpha )=-\varrho \ne 0$
we have $m\cos (\alpha )+\varrho \cos (2\alpha )=-\varrho \ne 0$![]() . Furthermore, for $\cos (\alpha ) \ne 0$
. Furthermore, for $\cos (\alpha ) \ne 0$![]() we have $m\cos (\alpha )+\varrho \cos (2\alpha ) \ne 0$
we have $m\cos (\alpha )+\varrho \cos (2\alpha ) \ne 0$![]() for $m$
for $m$![]() large enough. Consequently, $\tan (\beta _m)$
large enough. Consequently, $\tan (\beta _m)$![]() is (4.4) is well defined, i.e. $\beta _m \notin \{{\pi }/{2}, {3\pi }/{2}\}$
is (4.4) is well defined, i.e. $\beta _m \notin \{{\pi }/{2}, {3\pi }/{2}\}$![]() . Since $\tan (\beta _m) \ne 0$
. Since $\tan (\beta _m) \ne 0$![]() , we must have
, we must have
Also, from (4.4) it follows that
for each sufficiently large $m \in {\mathbb {N}}$![]() .
.
Now, from (4.4) we deduce
In case $\cos (\alpha )\tan (\beta _m)-\sin (\alpha )=0$![]() we have $\cos (\alpha ) \ne 0$
we have $\cos (\alpha ) \ne 0$![]() , and hence $\tan (\beta _m) =\tan (\alpha )$
, and hence $\tan (\beta _m) =\tan (\alpha )$![]() . By (4.6), this implies
. By (4.6), this implies
which is not the case in view of $\alpha \notin \{0, \pi \}$![]() . Therefore,
. Therefore,
Assume that $\beta _m=r_m \pi$![]() with rational number
with rational number
By (4.5), all values of $\tan (r_m \pi )$![]() belong to the field $F$
belong to the field $F$![]() . Thus, the degree of the algebraic number $\tan (r_m \pi )$
. Thus, the degree of the algebraic number $\tan (r_m \pi )$![]() is bounded from above by a constant, say $c_1=c_1(F)=[F:{\mathbb {Q}}]=c_1(s)$
is bounded from above by a constant, say $c_1=c_1(F)=[F:{\mathbb {Q}}]=c_1(s)$![]() . The exact degree of $\tan (r_m \pi )$
. The exact degree of $\tan (r_m \pi )$![]() with rational $r_m$
with rational $r_m$![]() in terms of the denominator $v$
in terms of the denominator $v$![]() of $r_m$
of $r_m$![]() has been calculated, for instance, in [Reference Tangsupphathawat23, Proposition 4.1]. For $v>8$
has been calculated, for instance, in [Reference Tangsupphathawat23, Proposition 4.1]. For $v>8$![]() it is at least $\varphi (2v)/4$
it is at least $\varphi (2v)/4$![]() , where $\varphi$
, where $\varphi$![]() is Euler's totient function. From $\varphi (2v)/4< c_1$
is Euler's totient function. From $\varphi (2v)/4< c_1$![]() we find that $v < c_2$
we find that $v < c_2$![]() for some $c_2$
for some $c_2$![]() depending in $s$
depending in $s$![]() only.
only.
Note that, by (4.8), the numerator of $r_m$![]() is less than $2v$
is less than $2v$![]() . Thus, there are only finitely many of such rational numbers $r_m$
. Thus, there are only finitely many of such rational numbers $r_m$![]() satisfying (4.8). Hence, as $s=\varrho e^{i \alpha }$
satisfying (4.8). Hence, as $s=\varrho e^{i \alpha }$![]() is fixed, there a constant $c_3=c_3(F)=c_3(s)>0$
is fixed, there a constant $c_3=c_3(F)=c_3(s)>0$![]() such that the quotient of
such that the quotient of
which is nonzero by (4.7), takes at most $c_3$![]() distinct values. However, by (4.6), this quotient equals $m$
distinct values. However, by (4.6), this quotient equals $m$![]() . This is clearly impossible for $m$
. This is clearly impossible for $m$![]() large enough.
large enough.
In the next lemma we show the existence of infinitely many triplets of useful complex points such that the point $z=0$![]() belongs to the interior of a triangle with vertices at each of these triplets.
belongs to the interior of a triangle with vertices at each of these triplets.
Lemma 4.3 Let $t=|t|e^{i\beta } \in {\mathbb {C}}$![]() , where the argument $\beta \in [0, 2\pi )$
, where the argument $\beta \in [0, 2\pi )$![]() of $t$
of $t$![]() satisfies ${\beta }/{\pi } \notin {\mathbb {Q}}$
satisfies ${\beta }/{\pi } \notin {\mathbb {Q}}$![]() . Then, there are infinitely many prime numbers $k$
. Then, there are infinitely many prime numbers $k$![]() such that the point $z=0$
such that the point $z=0$![]() belongs to the interior of a triangle with vertices at $t^k, t^{2k}, t^{3k}$
belongs to the interior of a triangle with vertices at $t^k, t^{2k}, t^{3k}$![]() , and also to the interior of a triangle with vertices at $t^{2k}, t^{4k}, t^{6k}$
, and also to the interior of a triangle with vertices at $t^{2k}, t^{4k}, t^{6k}$![]() .
.
Proof. For $\theta \in {\mathbb {R}} \setminus {\mathbb {Q}}$![]() the sequence of the fractional parts $\{\theta k\}$
the sequence of the fractional parts $\{\theta k\}$![]() , where $k$
, where $k$![]() runs over the primes, is everywhere dense in the interval $[0, 1]$
runs over the primes, is everywhere dense in the interval $[0, 1]$![]() . See, e.g., [Reference Strauch and Porubský22, Section 2–70]. (In fact, by an old result of Vinogradov, this sequence is uniformly distributed in $[0, 1]$
. See, e.g., [Reference Strauch and Porubský22, Section 2–70]. (In fact, by an old result of Vinogradov, this sequence is uniformly distributed in $[0, 1]$![]() .)
.)
In particular, as ${\beta }/{2\pi } \notin {\mathbb {Q}}$![]() , for each $\delta >0$
, for each $\delta >0$![]() , there are infinitely many prime numbers $k$
, there are infinitely many prime numbers $k$![]() such that
such that
Consequently, for each of those $k$![]() there is $\ell =\ell (k) \in {\mathbb {Z}}$
there is $\ell =\ell (k) \in {\mathbb {Z}}$![]() such that ${1}/{3}<{k\beta }/{2\pi }-\ell <{1}/{3}+\delta$
such that ${1}/{3}<{k\beta }/{2\pi }-\ell <{1}/{3}+\delta$![]() , which is equivalent to
, which is equivalent to
This means that the arguments of the complex numbers $t^k=|t|^k e^{ik\beta }$![]() , $t^{2k}$
, $t^{2k}$![]() , $t^{3k}$
, $t^{3k}$![]() lie in the intervals
lie in the intervals
respectively. It is clear that for $\delta >0$![]() small enough the point $z=0$
small enough the point $z=0$![]() belongs to the interior of a triangle with vertices at $t^k, t^{2k}, t^{3k}$
belongs to the interior of a triangle with vertices at $t^k, t^{2k}, t^{3k}$![]() .
.
Likewise, by (4.10), we see that the arguments of the complex numbers $t^{2k}=|t|^{2k} e^{2ik\beta }$![]() , $t^{4k}$
, $t^{4k}$![]() , $t^{6k}$
, $t^{6k}$![]() lie in the intervals
lie in the intervals
respectively. Again, for $\delta >0$![]() small enough, the point $z=0$
small enough, the point $z=0$![]() belongs to the interior of a triangle with vertices at $t^{2k}, t^{4k}, t^{6k}$
belongs to the interior of a triangle with vertices at $t^{2k}, t^{4k}, t^{6k}$![]() .
.
The following lemma will be useful in treating exceptional numbers in theorem 1.5.
Lemma 4.4 Let $\lambda \ne 0$![]() and $\psi$
and $\psi$![]() be two real algebraic numbers. Assume that for each sufficiently large $m \in {\mathbb {N}}$
be two real algebraic numbers. Assume that for each sufficiently large $m \in {\mathbb {N}}$![]() the number $\lambda (\lambda +m\psi +m^2)$
the number $\lambda (\lambda +m\psi +m^2)$![]() is rational or quadratic. Then, there is a real quadratic field $E$
is rational or quadratic. Then, there is a real quadratic field $E$![]() such that $\lambda, \psi \in E$
such that $\lambda, \psi \in E$![]() .
.
Proof. Set $F={\mathbb {Q}}(\lambda, \psi )$![]() . By the assumption of the lemma, the numbers
. By the assumption of the lemma, the numbers
where $m \in {\mathbb {N}}$![]() is large enough, are all at most quadratic, and all belong to $F$
is large enough, are all at most quadratic, and all belong to $F$![]() . Since $F$
. Since $F$![]() has only finitely many real quadratic subfields (possibly none), there is a real quadratic field $E$
has only finitely many real quadratic subfields (possibly none), there is a real quadratic field $E$![]() and an infinite set $M \subset {\mathbb {N}}$
and an infinite set $M \subset {\mathbb {N}}$![]() such that $\tau _m \in E$
such that $\tau _m \in E$![]() for each $m \in M$
for each $m \in M$![]() . (In the case when all the numbers $\tau _m$
. (In the case when all the numbers $\tau _m$![]() are rational, we can take any real quadratic field $E$
are rational, we can take any real quadratic field $E$![]() .) Select $m \ne m'$
.) Select $m \ne m'$![]() in $M$
in $M$![]() . Then,
. Then,
and hence $\lambda ^2-mm'\lambda \in E$![]() . Taking $m' \in M \setminus \{m, m'\}$
. Taking $m' \in M \setminus \{m, m'\}$![]() , by the same argument, we obtain $\lambda ^2-mm' \lambda \in E$
, by the same argument, we obtain $\lambda ^2-mm' \lambda \in E$![]() . The difference $m(m''-m') \lambda$
. The difference $m(m''-m') \lambda$![]() of these two numbers is also in $E$
of these two numbers is also in $E$![]() , which forces $\lambda \in E$
, which forces $\lambda \in E$![]() . Since $\lambda \ne 0$
. Since $\lambda \ne 0$![]() and $\tau _m \in E$
and $\tau _m \in E$![]() , we also obtain
, we also obtain
which completes the proof of the lemma.
The next lemma gives one more approach to establishing the density of a sumset in ${\mathbb {C}}$![]() . This time we will use four sets instead of three. This lemma will be used in the final part of the proof of theorem 1.5.
. This time we will use four sets instead of three. This lemma will be used in the final part of the proof of theorem 1.5.
Lemma 4.5 Let $s \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() . Assume that the set ${\mathbb {N}}[s]$
. Assume that the set ${\mathbb {N}}[s]$![]() contains two elements $s_1, s_2 \ne 0$
contains two elements $s_1, s_2 \ne 0$![]() whose quotient $\omega ={s_1}/{s_2}$
whose quotient $\omega ={s_1}/{s_2}$![]() is a negative real irrational number. Then, the sumset
is a negative real irrational number. Then, the sumset
is everywhere dense in ${\mathbb {C}}$![]() .
.
Proof. Since the points $0, s_2, s_2 s$![]() are not collinear, every complex number can be written in the form $Xs_2+Ys_2 s$
are not collinear, every complex number can be written in the form $Xs_2+Ys_2 s$![]() with $X, Y \in {\mathbb {R}}$
with $X, Y \in {\mathbb {R}}$![]() . The idea is to approximate $Xs_2$
. The idea is to approximate $Xs_2$![]() by the sumset ${\mathbb {N}} s_1+{\mathbb {N}} s_2$
by the sumset ${\mathbb {N}} s_1+{\mathbb {N}} s_2$![]() and $Ys_2 s$
and $Ys_2 s$![]() by the sumset ${\mathbb {N}} s_1s+{\mathbb {N}} s_2 s$
by the sumset ${\mathbb {N}} s_1s+{\mathbb {N}} s_2 s$![]() .
.
We will show that for each $\varepsilon >0$![]() there exist $a_1, a_2, a_3, a_4 \in {\mathbb {N}}$
there exist $a_1, a_2, a_3, a_4 \in {\mathbb {N}}$![]() such that
such that
Since $s_1=\omega s_2$![]() , setting
, setting
and using the identities $X=-[-X]-\{-X\}$![]() , $Y=-[-Y]-\{-Y\}$
, $Y=-[-Y]-\{-Y\}$![]() , we can rewrite the inequalities in (4.11) as
, we can rewrite the inequalities in (4.11) as
By lemma 3.1 with $N=1$![]() and $\lambda _1=-\omega$
and $\lambda _1=-\omega$![]() , we see that for each $\varepsilon _1>0$
, we see that for each $\varepsilon _1>0$![]() there is $a_1 \in {\mathbb {N}}$
there is $a_1 \in {\mathbb {N}}$![]() and $b_1 \in {\mathbb {Z}}$
and $b_1 \in {\mathbb {Z}}$![]() such that
such that
Here, for each sufficiently small $\varepsilon _1$![]() , the integer $a_1 \in {\mathbb {N}}$
, the integer $a_1 \in {\mathbb {N}}$![]() must be large. Since $-\omega >0$
must be large. Since $-\omega >0$![]() , the integer $b_1$
, the integer $b_1$![]() is positive and large. So the first displayed inequality indeed holds with $a_2=b_1-[-X] \in {\mathbb {N}}$
is positive and large. So the first displayed inequality indeed holds with $a_2=b_1-[-X] \in {\mathbb {N}}$![]() . This proves the first inequality in (4.11). The proof of the second displayed inequality is exactly the same, with some $a_3, a_4 \in {\mathbb {N}}$
. This proves the first inequality in (4.11). The proof of the second displayed inequality is exactly the same, with some $a_3, a_4 \in {\mathbb {N}}$![]() , which implies the second inequality in (4.11).
, which implies the second inequality in (4.11).
5. Final preparation
In this section we will prove the following proposition:
Proposition 5.1 Let $t=|t|e^{i\beta } \in {\mathbb {C}}$![]() be such that ${\beta }/{\pi } \notin {\mathbb {Q}}$
be such that ${\beta }/{\pi } \notin {\mathbb {Q}}$![]() and $|t|^2$
and $|t|^2$![]() is not an algebraic number of degree at most $2$
is not an algebraic number of degree at most $2$![]() . Then, there is a positive integer $n$
. Then, there is a positive integer $n$![]() such that the sumset
such that the sumset
is everywhere dense in ${\mathbb {C}}$![]() .
.
Proof. Set $\xi =|t|^2$![]() . We claim that $\xi ^k$
. We claim that $\xi ^k$![]() is not an algebraic number of degree at most $2$
is not an algebraic number of degree at most $2$![]() for all sufficiently large prime numbers $k$
for all sufficiently large prime numbers $k$![]() . This is trivial if $\xi$
. This is trivial if $\xi$![]() is transcendental. Assume that $\xi$
is transcendental. Assume that $\xi$![]() is an algebraic number of degree $d$
is an algebraic number of degree $d$![]() . By the condition of the proposition, we have $d \geq 3$
. By the condition of the proposition, we have $d \geq 3$![]() . Evidently, the degree of $\xi ^k$
. Evidently, the degree of $\xi ^k$![]() is $d$
is $d$![]() , unless there is a conjugate $\xi ' \ne \xi$
, unless there is a conjugate $\xi ' \ne \xi$![]() of $\xi$
of $\xi$![]() over ${\mathbb {Q}}$
over ${\mathbb {Q}}$![]() such that $\xi ^k=\xi '^k$
such that $\xi ^k=\xi '^k$![]() . But then $\zeta =\xi /\xi '$
. But then $\zeta =\xi /\xi '$![]() is a $k$
is a $k$![]() th root of unity, so its degree is $\varphi (k)=k-1$
th root of unity, so its degree is $\varphi (k)=k-1$![]() . However, the number $\zeta$
. However, the number $\zeta$![]() cannot belong to the field ${\mathbb {Q}}(\xi, \xi ')$
cannot belong to the field ${\mathbb {Q}}(\xi, \xi ')$![]() of degree at most $d(d-1)$
of degree at most $d(d-1)$![]() when $k>d(d-1)$
when $k>d(d-1)$![]() , a contradiction. Thus, $\xi ^k$
, a contradiction. Thus, $\xi ^k$![]() is of degree $d$
is of degree $d$![]() ($d \geq 3$
($d \geq 3$![]() ) for each sufficiently large prime number $k$
) for each sufficiently large prime number $k$![]() .
.
Since the argument $\beta$![]() of a given number $t$
of a given number $t$![]() satisfies the condition of lemma 4.3, there are infinitely many primes $k$
satisfies the condition of lemma 4.3, there are infinitely many primes $k$![]() for which $z=0$
for which $z=0$![]() belongs to the interior of the triangles with vertices at $t^k, t^{2k}, t^{3k}$
belongs to the interior of the triangles with vertices at $t^k, t^{2k}, t^{3k}$![]() and at $t^{2k}, t^{4k}, t^{6k}$
and at $t^{2k}, t^{4k}, t^{6k}$![]() .
.
Take any $n \in \{k, 2k\}$![]() . By theorem 1.9, the set
. By theorem 1.9, the set
is everywhere dense in ${\mathbb {C}}$![]() if the imaginary parts
if the imaginary parts

are linearly independent over ${\mathbb {Q}}$![]() . We will show that this is the case for either $n=k$
. We will show that this is the case for either $n=k$![]() or $n=2k$
or $n=2k$![]() .
.
Since the number ${\beta }/{\pi }$![]() is irrational, we have $\sin (n\beta ) \ne 0$
is irrational, we have $\sin (n\beta ) \ne 0$![]() and $\cos (n\beta ) \ne 0$
and $\cos (n\beta ) \ne 0$![]() . Dividing by $-|t|^{3n} \sin (n\beta )$
. Dividing by $-|t|^{3n} \sin (n\beta )$![]() , we see that the above three numbers are linearly dependent over ${\mathbb {Q}}$
, we see that the above three numbers are linearly dependent over ${\mathbb {Q}}$![]() if and only if so are $1, |t|^{2n}, -2|t|^n \cos (n\beta )$
if and only if so are $1, |t|^{2n}, -2|t|^n \cos (n\beta )$![]() . This is the case if and only if the numbers
. This is the case if and only if the numbers
are linearly dependent over ${\mathbb {Q}}$![]() .
.
We claim that the numbers $|t|^{-n}$![]() and $|t|^n$
and $|t|^n$![]() are linearly independent over ${\mathbb {Q}}$
are linearly independent over ${\mathbb {Q}}$![]() . This is trivial if $\xi =|t|^2$
. This is trivial if $\xi =|t|^2$![]() is transcendental. Assume that $\xi$
is transcendental. Assume that $\xi$![]() is algebraic of degree $d \geq 3$
is algebraic of degree $d \geq 3$![]() . Consider the cases $n=k$
. Consider the cases $n=k$![]() and $n=2k$
and $n=2k$![]() separately. If $n=k$
separately. If $n=k$![]() then the numbers $|t|^{-n}$
then the numbers $|t|^{-n}$![]() and $|t|^n$
and $|t|^n$![]() are linearly dependent if and only if $|t|^{2n}=|t|^{2k}=\xi ^k \in {\mathbb {Q}}$
are linearly dependent if and only if $|t|^{2n}=|t|^{2k}=\xi ^k \in {\mathbb {Q}}$![]() . However, we proved that the degree of $\xi ^k$
. However, we proved that the degree of $\xi ^k$![]() is $d \geq 3$
is $d \geq 3$![]() . So, the numbers $|t|^{-n}$
. So, the numbers $|t|^{-n}$![]() and $|t|^n$
and $|t|^n$![]() are linearly independent for $n=k$
are linearly independent for $n=k$![]() . Similarly, for $n=2k$
. Similarly, for $n=2k$![]() , the numbers $|t|^{-n}$
, the numbers $|t|^{-n}$![]() and $|t|^n$
and $|t|^n$![]() are linearly dependent if and only if $|t|^{2n}=|t|^{4k}=\xi ^{2k} \in {\mathbb {Q}}$
are linearly dependent if and only if $|t|^{2n}=|t|^{4k}=\xi ^{2k} \in {\mathbb {Q}}$![]() . This is only possible if the degree of $\xi ^k$
. This is only possible if the degree of $\xi ^k$![]() over ${\mathbb {Q}}$
over ${\mathbb {Q}}$![]() is $1$
is $1$![]() or $2$
or $2$![]() , while we know that it is $d \geq 3$
, while we know that it is $d \geq 3$![]() . Thus, the numbers $|t|^{-n}$
. Thus, the numbers $|t|^{-n}$![]() and $|t|^n$
and $|t|^n$![]() are linearly independent for $n=2k$
are linearly independent for $n=2k$![]() as well.
as well.
Now, by the linear dependence of the three numbers (5.1), it follows that in both cases $n=k$![]() and $n=2k$
and $n=2k$![]() for some $\mu _n, \nu _n \in {\mathbb {Q}}$
for some $\mu _n, \nu _n \in {\mathbb {Q}}$![]() , we must have
, we must have
In order to complete the proof of the proposition it suffices to show that (5.2) cannot hold for both $n=k$![]() and for $n=2k$
and for $n=2k$![]() . Assume that (5.2) is true for $n=k$
. Assume that (5.2) is true for $n=k$![]() and for $n=2k$
and for $n=2k$![]() . Then, by (5.2), applying the trigonometric identity $\cos (2k\beta )=2\cos ^2(k\beta )-1$
. Then, by (5.2), applying the trigonometric identity $\cos (2k\beta )=2\cos ^2(k\beta )-1$![]() and using the notation $x=|t|^{k}$
and using the notation $x=|t|^{k}$![]() , $\mu '=\mu _{2k}$
, $\mu '=\mu _{2k}$![]() , $\nu '=\nu _{2k}$
, $\nu '=\nu _{2k}$![]() , $\mu =\mu _{k}$
, $\mu =\mu _{k}$![]() , $\nu =\nu _k$
, $\nu =\nu _k$![]() , we find that
, we find that
This is equivalent to
Now, since $x^2=|t|^{2k}=\xi ^k$![]() is either transcendental or an algebraic number of degree $d \geq 3$
is either transcendental or an algebraic number of degree $d \geq 3$![]() and $\mu '-\mu, \nu '-\nu ^2, \mu \nu -1 \in {\mathbb {Q}}$
and $\mu '-\mu, \nu '-\nu ^2, \mu \nu -1 \in {\mathbb {Q}}$![]() , equality (5.3) must be the identity in $x$
, equality (5.3) must be the identity in $x$![]() . Hence, $\mu '=\mu ^2$
. Hence, $\mu '=\mu ^2$![]() , $\nu '=\nu ^2$
, $\nu '=\nu ^2$![]() and $\mu \nu =1$
and $\mu \nu =1$![]() . In particular, from $\mu \nu =1$
. In particular, from $\mu \nu =1$![]() we see that both $\mu =\mu _k$
we see that both $\mu =\mu _k$![]() and $\nu =\nu _k$
and $\nu =\nu _k$![]() have the same sign.
have the same sign.
If they are both positive then, by (5.2) with $n=k$![]() and $\mu _k\nu _k=1$
and $\mu _k\nu _k=1$![]() , we derive that
, we derive that
Therefore, $\cos (k \beta )=1$![]() , which implies that ${\beta }/{\pi } \in {\mathbb {Q}}$
, which implies that ${\beta }/{\pi } \in {\mathbb {Q}}$![]() , a contradiction. Similarly, if $\mu _k$
, a contradiction. Similarly, if $\mu _k$![]() and $\nu _k$
and $\nu _k$![]() are both negative, then from $-\mu _k>0$
are both negative, then from $-\mu _k>0$![]() , $-\nu _k>0$
, $-\nu _k>0$![]() and $\mu _k \nu _k=1$
and $\mu _k \nu _k=1$![]() we deduce
we deduce
and hence $\cos (k\beta )=-1$![]() . Hence, ${\beta }/{\pi } \in {\mathbb {Q}}$
. Hence, ${\beta }/{\pi } \in {\mathbb {Q}}$![]() , which is again a contradiction. This completes the proof of the proposition.
, which is again a contradiction. This completes the proof of the proposition.
6. Proof of theorem 1.3
Let $s \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() be a transcendental number. By lemma 4.1, for some $t \in \{s, s+s^2\}$
be a transcendental number. By lemma 4.1, for some $t \in \{s, s+s^2\}$![]() the three numbers $t=|t|e^{i\beta }$
the three numbers $t=|t|e^{i\beta }$![]() , $|t|$
, $|t|$![]() and $t/|t|=e^{i\beta }$
and $t/|t|=e^{i\beta }$![]() are all transcendental. In particular, this implies that the quotient ${\beta }/{\pi }$
are all transcendental. In particular, this implies that the quotient ${\beta }/{\pi }$![]() is irrational and that $|t|^2$
is irrational and that $|t|^2$![]() is not an algebraic number of degree at most $2$
is not an algebraic number of degree at most $2$![]() . Thus, proposition 5.1 yields theorem 1.3 for transcendental $s$
. Thus, proposition 5.1 yields theorem 1.3 for transcendental $s$![]() .
.
Assume now that $s \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() is algebraic and has degree $d$
is algebraic and has degree $d$![]() over ${\mathbb {Q}}$
over ${\mathbb {Q}}$![]() . Clearly, $d \ne 1$
. Clearly, $d \ne 1$![]() . Also, $d \ne 2$
. Also, $d \ne 2$![]() by the condition of the theorem. By lemma 4.2, we can take a sufficiently large $m \in {\mathbb {N}}$
by the condition of the theorem. By lemma 4.2, we can take a sufficiently large $m \in {\mathbb {N}}$![]() such that the argument $\beta _m$
such that the argument $\beta _m$![]() of $t=ms+s^2$
of $t=ms+s^2$![]() satisfies ${\beta _m}/{\pi } \notin {\mathbb {Q}}$
satisfies ${\beta _m}/{\pi } \notin {\mathbb {Q}}$![]() . Now, proposition 5.1 implies theorem 1.3 in case for at least one sufficiently large $m \in {\mathbb {N}}$
. Now, proposition 5.1 implies theorem 1.3 in case for at least one sufficiently large $m \in {\mathbb {N}}$![]() the algebraic number $|ms+s^2|^2$
the algebraic number $|ms+s^2|^2$![]() has degree greater than $2$
has degree greater than $2$![]() .
.
For a contradiction, assume that all numbers
$m \geq m_0$![]() , are of degree at most $2$
, are of degree at most $2$![]() . Setting $\lambda =s \overline {s}$
. Setting $\lambda =s \overline {s}$![]() and $\psi =s+\overline {s}$
and $\psi =s+\overline {s}$![]() , by lemma 4.4, we see that there is a real quadratic field $E$
, by lemma 4.4, we see that there is a real quadratic field $E$![]() such that $\lambda, \psi \in E$
such that $\lambda, \psi \in E$![]() . Since $s$
. Since $s$![]() is the root of
is the root of
and $s$![]() is of degree $d>2$
is of degree $d>2$![]() , at least one of the numbers $\lambda, \psi$
, at least one of the numbers $\lambda, \psi$![]() must be quadratic (otherwise $x^2-\psi x+\lambda \in {\mathbb {Q}}[x]$
must be quadratic (otherwise $x^2-\psi x+\lambda \in {\mathbb {Q}}[x]$![]() and $d \leq 2$
and $d \leq 2$![]() ).
).
Now, we will show that such $s$![]() must be exceptional. For this, by (1.5), it suffices to show that $s$
must be exceptional. For this, by (1.5), it suffices to show that $s$![]() is quartic. Assume that the conjugates of $\lambda$
is quartic. Assume that the conjugates of $\lambda$![]() and $\psi$
and $\psi$![]() over ${\mathbb {Q}}$
over ${\mathbb {Q}}$![]() are $\lambda '$
are $\lambda '$![]() and $\psi '$
and $\psi '$![]() respectively. Here, $\lambda '=\lambda$
respectively. Here, $\lambda '=\lambda$![]() if $\lambda \in {\mathbb {Q}}$
if $\lambda \in {\mathbb {Q}}$![]() and $\psi '=\psi$
and $\psi '=\psi$![]() if $\psi \in {\mathbb {Q}}$
if $\psi \in {\mathbb {Q}}$![]() . By the above, we must have either $\lambda ' \ne \lambda$
. By the above, we must have either $\lambda ' \ne \lambda$![]() or $\psi ' \ne \psi$
or $\psi ' \ne \psi$![]() (or both). With this notation, it follows that $s$
(or both). With this notation, it follows that $s$![]() is a root of the polynomial
is a root of the polynomial
If the polynomial $Q$![]() were reducible over ${\mathbb {Q}}$
were reducible over ${\mathbb {Q}}$![]() then its irreducible factor with the root $s$
then its irreducible factor with the root $s$![]() must be cubic. So $Q$
must be cubic. So $Q$![]() must have a rational root. However, if $r \in {\mathbb {Q}}$
must have a rational root. However, if $r \in {\mathbb {Q}}$![]() is a root of $Q$
is a root of $Q$![]() , then, by (6.1),
, then, by (6.1),
Taking an automorphism of the Galois group ${\rm Gal}(E/{\mathbb {Q}})$![]() that maps $\lambda$
that maps $\lambda$![]() to $\lambda '$
to $\lambda '$![]() and so $\psi$
and so $\psi$![]() to $\psi '$
to $\psi '$![]() (or vice versa) we see that both displayed equalities must hold. Hence, $r$
(or vice versa) we see that both displayed equalities must hold. Hence, $r$![]() is at least a double root of $Q$
is at least a double root of $Q$![]() , so $s$
, so $s$![]() cannot be cubic. This proves that $Q$
cannot be cubic. This proves that $Q$![]() is irreducible over ${\mathbb {Q}}$
is irreducible over ${\mathbb {Q}}$![]() , and hence $s$
, and hence $s$![]() is a quartic number ($d=4$
is a quartic number ($d=4$![]() ), which is not allowed by the condition of the theorem. This completes the proof of theorem 1.3.
), which is not allowed by the condition of the theorem. This completes the proof of theorem 1.3.
7. Proof of theorem 1.5
Note that in the previous section we have proved the required result for the first part of the theorem for all quartic numbers $s$![]() as well except for those with minimal polynomial $Q$
as well except for those with minimal polynomial $Q$![]() defined in (6.1). By (1.5) and the irreducibility of $Q$
defined in (6.1). By (1.5) and the irreducibility of $Q$![]() , these are exactly exceptional numbers.
, these are exactly exceptional numbers.
To prove the second part of the theorem we assume that for some exceptional $s$![]() and some $s_1, s_2, s_3 \in {\mathbb {N}}[s]$
and some $s_1, s_2, s_3 \in {\mathbb {N}}[s]$![]() the sumset (1.6) is everywhere dense in ${\mathbb {C}}$
the sumset (1.6) is everywhere dense in ${\mathbb {C}}$![]() . Then, by theorem 1.9, the imaginary parts
. Then, by theorem 1.9, the imaginary parts
must be linearly independent over ${\mathbb {Q}}$![]() . Since $s=\varrho e^{i\alpha } \in {\mathbb {C}} \setminus {\mathbb {R}}$
. Since $s=\varrho e^{i\alpha } \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() , we have $\varrho \sin (\alpha ) \ne 0$
, we have $\varrho \sin (\alpha ) \ne 0$![]() , so that the three numbers
, so that the three numbers
must be linearly independent over ${\mathbb {Q}}$![]() . As $s$
. As $s$![]() is exceptional, by (1.5), there is a real quadratic number field $E$
is exceptional, by (1.5), there is a real quadratic number field $E$![]() such that
such that
Below, we will show that the numbers in (7.1) all belong to $E$![]() . Since $E$
. Since $E$![]() is quadratic, any three (not necessarily distinct) numbers in $E$
is quadratic, any three (not necessarily distinct) numbers in $E$![]() must be linearly dependent. This contradicts the linear independence of the three numbers (7.1).
must be linearly dependent. This contradicts the linear independence of the three numbers (7.1).
Indeed, write $s_1=\sum _{i \in I} a_i s^i$![]() and $s_2=\sum _{j \in J} b_j s^j$
and $s_2=\sum _{j \in J} b_j s^j$![]() , where $I, J$
, where $I, J$![]() are some finite subsets of ${\mathbb {N}}$
are some finite subsets of ${\mathbb {N}}$![]() and $a_i, b_j \in {\mathbb {N}}$
and $a_i, b_j \in {\mathbb {N}}$![]() for $i \in I$
for $i \in I$![]() , $j \in J$
, $j \in J$![]() . Note that
. Note that
The terms with $i=j$![]() are all equal to zero. So the first number on the list (7.1) is the sum of several terms of the form
are all equal to zero. So the first number on the list (7.1) is the sum of several terms of the form
where $i>j$![]() and $c_{i,j} \in {\mathbb {Z}}$
and $c_{i,j} \in {\mathbb {Z}}$![]() . It is well known that the quotient ${\sin ((i-j)\alpha )}/{\sin (\alpha )}$
. It is well known that the quotient ${\sin ((i-j)\alpha )}/{\sin (\alpha )}$![]() is $U_{i-j-1}(\cos (\alpha ))$
is $U_{i-j-1}(\cos (\alpha ))$![]() , where $U_0(x)=1$
, where $U_0(x)=1$![]() and
and

is the Chebyshev polynomial of the second kind for $n \in {\mathbb {N}}$![]() . Therefore, ${\Im (s_1 \overline {s_2})}/{\varrho \sin (\alpha )}$
. Therefore, ${\Im (s_1 \overline {s_2})}/{\varrho \sin (\alpha )}$![]() is the sum of integral multiples of several terms of the form
is the sum of integral multiples of several terms of the form
where $i, j, k$![]() are positive integers satisfying $i-j-2k+1 \geq 0$
are positive integers satisfying $i-j-2k+1 \geq 0$![]() . Note that
. Note that
where the factors $\varrho ^{2j+2k-2}$![]() and $(\varrho \cos (\alpha ))^{i-j-2k+1}$
and $(\varrho \cos (\alpha ))^{i-j-2k+1}$![]() are both in $E$
are both in $E$![]() by (7.2). Consequently, the first number in (7.1) belongs to $E$
by (7.2). Consequently, the first number in (7.1) belongs to $E$![]() . By exactly the same argument, the second and the third numbers in (7.1) are also in $E$
. By exactly the same argument, the second and the third numbers in (7.1) are also in $E$![]() . This completes the proof of the second part of theorem 1.5.
. This completes the proof of the second part of theorem 1.5.
In all that follows we will prove that for a quartic exceptional number $s \in {\mathbb {C}} \setminus {\mathbb {R}}$![]() , whose minimal polynomial (6.1) has two nonreal roots $s$
, whose minimal polynomial (6.1) has two nonreal roots $s$![]() , $\overline {s}$
, $\overline {s}$![]() , and two other roots $s', s''$
, and two other roots $s', s''$![]() , there exist $t_1, t_2, t_3, t_4 \in {\mathbb {N}}[s]$
, there exist $t_1, t_2, t_3, t_4 \in {\mathbb {N}}[s]$![]() such that the sumset (1.7) is everywhere dense in ${\mathbb {C}}$
such that the sumset (1.7) is everywhere dense in ${\mathbb {C}}$![]() . We remark that the density of ${\mathbb {N}}[s]$
. We remark that the density of ${\mathbb {N}}[s]$![]() in ${\mathbb {C}}$
in ${\mathbb {C}}$![]() for some quartic numbers $s$
for some quartic numbers $s$![]() with minimal polynomial (6.1) can be established by corollary 2.2. Indeed, for a quartic $s$
with minimal polynomial (6.1) can be established by corollary 2.2. Indeed, for a quartic $s$![]() with minimal polynomial (6.1), corollary 2.2 implies the density of ${\mathbb {N}}[s]$
with minimal polynomial (6.1), corollary 2.2 implies the density of ${\mathbb {N}}[s]$![]() in ${\mathbb {C}}$
in ${\mathbb {C}}$![]() in the case when $s$
in the case when $s$![]() has no real positive conjugates over ${\mathbb {Q}}$
has no real positive conjugates over ${\mathbb {Q}}$![]() . However, the result that we are going to prove is stronger, since in (1.7) we only use the sumset of four sets.
. However, the result that we are going to prove is stronger, since in (1.7) we only use the sumset of four sets.
Firstly, by lemma 4.2, we can replace $s$![]() by $ms+s^2$
by $ms+s^2$![]() with appropriate sufficiently large $m \in {\mathbb {N}}$
with appropriate sufficiently large $m \in {\mathbb {N}}$![]() such that the argument $\beta$
such that the argument $\beta$![]() of $ms+s^2$
of $ms+s^2$![]() satisfies ${\beta }/{\pi } \notin {\mathbb {Q}}$
satisfies ${\beta }/{\pi } \notin {\mathbb {Q}}$![]() . Then, $ms+s^2 \ne m \overline {s}+\overline {s}^2$
. Then, $ms+s^2 \ne m \overline {s}+\overline {s}^2$![]() , so $ms+s^2$
, so $ms+s^2$![]() is a quartic exceptional number by (1.5). Since ${\mathbb {N}}[ms+s^2] \subseteq {\mathbb {N}}[s]$
is a quartic exceptional number by (1.5). Since ${\mathbb {N}}[ms+s^2] \subseteq {\mathbb {N}}[s]$![]() , we can further argue with the number $ms+s^2$
, we can further argue with the number $ms+s^2$![]() , which we denote by $s$
, which we denote by $s$![]() . Its conjugates are $\overline {s}, s', s''$
. Its conjugates are $\overline {s}, s', s''$![]() , its minimal polynomial is (6.1), and its argument $\beta$
, its minimal polynomial is (6.1), and its argument $\beta$![]() satisfies ${\beta }/{\pi } \notin {\mathbb {Q}}$
satisfies ${\beta }/{\pi } \notin {\mathbb {Q}}$![]() .
.
Assume first $\lambda =s \overline {s}$![]() is a rational number. Since the argument $\beta$
is a rational number. Since the argument $\beta$![]() of $s$
of $s$![]() satisfies ${\beta }/{\pi } \notin {\mathbb {Q}}$
satisfies ${\beta }/{\pi } \notin {\mathbb {Q}}$![]() , as in lemma 4.3 (see (4.9)), we can select $l \in {\mathbb {N}}$
, as in lemma 4.3 (see (4.9)), we can select $l \in {\mathbb {N}}$![]() such that
such that
Then, for some $k \in {\mathbb {Z}}$![]() we get ${1}/{2}< {l\beta }/{2\pi }-k < {2}/{3}$
we get ${1}/{2}< {l\beta }/{2\pi }-k < {2}/{3}$![]() . Hence, $\pi < l\beta -2\pi k <{4\pi }/{3}$
. Hence, $\pi < l\beta -2\pi k <{4\pi }/{3}$![]() , which implies
, which implies
Note that $s^l \ne \overline {s}^l$![]() by the above-mentioned property of $\beta$
by the above-mentioned property of $\beta$![]() , so $s^l$
, so $s^l$![]() is exceptional. Since ${\mathbb {N}}[s^l] \subseteq {\mathbb {N}}[s]$
is exceptional. Since ${\mathbb {N}}[s^l] \subseteq {\mathbb {N}}[s]$![]() , it suffices to prove the density of (1.7) in ${\mathbb {C}}$
, it suffices to prove the density of (1.7) in ${\mathbb {C}}$![]() for $s$
for $s$![]() replaced by $s^l$
replaced by $s^l$![]() . We will write $s$
. We will write $s$![]() for $s^l$
for $s^l$![]() . For this $s$
. For this $s$![]() , we have $\lambda \in {\mathbb {Q}}$
, we have $\lambda \in {\mathbb {Q}}$![]() , $\lambda >0$
, $\lambda >0$![]() and $\psi =2|s|^l \cos (l\beta )<0$
and $\psi =2|s|^l \cos (l\beta )<0$![]() by (7.4). From $s^2-\psi s +\lambda =0$
by (7.4). From $s^2-\psi s +\lambda =0$![]() we thus obtain $\psi ={s^2+\lambda }/{s}$
we thus obtain $\psi ={s^2+\lambda }/{s}$![]() . Choosing $L \in {\mathbb {N}}$
. Choosing $L \in {\mathbb {N}}$![]() for which $L \lambda \in {\mathbb {N}}$
for which $L \lambda \in {\mathbb {N}}$![]() we deduce that the negative irrational number $\psi$
we deduce that the negative irrational number $\psi$![]() is a quotient of $s_1=Ls^3+L\lambda s \in {\mathbb {N}}[s]$
is a quotient of $s_1=Ls^3+L\lambda s \in {\mathbb {N}}[s]$![]() and $s_2=Ls^2 \in {\mathbb {N}}[s]$
and $s_2=Ls^2 \in {\mathbb {N}}[s]$![]() . By lemma 4.5, this proves (1.7) with the choice $t_1=s_1$
. By lemma 4.5, this proves (1.7) with the choice $t_1=s_1$![]() , $t_2=s_2$
, $t_2=s_2$![]() , $t_3=s_1 s$
, $t_3=s_1 s$![]() and $t_4=s_2 s$
and $t_4=s_2 s$![]() .
.
Assume now that $\lambda =s \overline {s}>0$![]() is irrational. Then, $\lambda \ne \lambda '=s' s''$
is irrational. Then, $\lambda \ne \lambda '=s' s''$![]() . We now reduce the problem to the case when the minimal polynomial $Q$
. We now reduce the problem to the case when the minimal polynomial $Q$![]() of $s$
of $s$![]() (as in (6.1)) has two nonreal roots $s, \overline {s}$
(as in (6.1)) has two nonreal roots $s, \overline {s}$![]() and two other roots $s', s''$
and two other roots $s', s''$![]() satisfying
satisfying
Consider the number $s^2$![]() , which we denote by $s$
, which we denote by $s$![]() . It is exceptional, with conjugates $\overline {s}, s', s''$
. It is exceptional, with conjugates $\overline {s}, s', s''$![]() . Note that for this number we have $\lambda '=s' s''>0$
. Note that for this number we have $\lambda '=s' s''>0$![]() (which was possibly negative in case the original $s$
(which was possibly negative in case the original $s$![]() had a positive and a negative conjugate). Since $\lambda \ne \lambda '$
had a positive and a negative conjugate). Since $\lambda \ne \lambda '$![]() , the third inequality in (7.5) is either true, or we have $\lambda <\lambda '$
, the third inequality in (7.5) is either true, or we have $\lambda <\lambda '$![]() . But in that case we can replace $s$
. But in that case we can replace $s$![]() by $s^{-1}$
by $s^{-1}$![]() (which is also exceptional). Then, the third inequality in (7.5) becomes true. Furthermore, if a real negative number $\omega$
(which is also exceptional). Then, the third inequality in (7.5) becomes true. Furthermore, if a real negative number $\omega$![]() is expressible by a quotient of two polynomials in the variable $s^{-1}$
is expressible by a quotient of two polynomials in the variable $s^{-1}$![]() with coefficients in ${\mathbb {N}}$
with coefficients in ${\mathbb {N}}$![]() , then, by multiplying these two polynomials by an appropriate power of $s$
, then, by multiplying these two polynomials by an appropriate power of $s$![]() , we see that the same number $\omega$
, we see that the same number $\omega$![]() is also a quotient of two polynomials in $s$
is also a quotient of two polynomials in $s$![]() with coefficients in ${\mathbb {N}}$
with coefficients in ${\mathbb {N}}$![]() . So, we can always assume that the third inequality in (7.5) is true.
. So, we can always assume that the third inequality in (7.5) is true.
Now, we will show that without the restriction of generality we may also assume the first two inequalities in (7.5). Indeed, if the conjugates $s', s''$![]() of $s$
of $s$![]() are both real, then we can choose an even integer $l$
are both real, then we can choose an even integer $l$![]() for which (7.3) holds. Then, (7.4) is also true, and we can replace $s$
for which (7.3) holds. Then, (7.4) is also true, and we can replace $s$![]() by $s^l$
by $s^l$![]() . Thus, replacing $s$
. Thus, replacing $s$![]() by $s^l$
by $s^l$![]() , which is exceptional, we find that the new $\psi$
, which is exceptional, we find that the new $\psi$![]() and $\psi '$
and $\psi '$![]() satisfy
satisfy
The new $\lambda$![]() , namely $\lambda ^l$
, namely $\lambda ^l$![]() , is still a positive rational number, satisfying $\lambda ^l>(\lambda ')^l$
, is still a positive rational number, satisfying $\lambda ^l>(\lambda ')^l$![]() . So all three inequalities in (7.5) hold.
. So all three inequalities in (7.5) hold.
Alternatively, if $s'$![]() and $s''$
and $s''$![]() are both nonreal, then they are complex conjugate numbers. Thus, they have the same modulus, say $\varrho '$
are both nonreal, then they are complex conjugate numbers. Thus, they have the same modulus, say $\varrho '$![]() , satisfying $\varrho '<|s|$
, satisfying $\varrho '<|s|$![]() in view of the third inequality in (7.5). In that case we choose $l \in {\mathbb {N}}$
in view of the third inequality in (7.5). In that case we choose $l \in {\mathbb {N}}$![]() satisfying (7.3) (and so (7.4)) and in addition so large that
satisfying (7.3) (and so (7.4)) and in addition so large that
Now, replacing $s$![]() by $s^l$
by $s^l$![]() , we find that
, we find that
where the (only) inequality above holds due to
This proves the second inequality in (7.5). The first inequality there, i.e. $\psi <0$![]() , is also true, since $\cos (l\beta )<0$
, is also true, since $\cos (l\beta )<0$![]() . This, replacing $s$
. This, replacing $s$![]() by $s^l$
by $s^l$![]() , reduces the problem to the case of exceptional numbers satisfying (7.5).
, reduces the problem to the case of exceptional numbers satisfying (7.5).
In order to apply lemma 4.5 we will show that there is a negative real irrational number expressible by two nonzero elements $s_1, s_2$![]() of ${\mathbb {N}}[s]$
of ${\mathbb {N}}[s]$![]() for $s$
for $s$![]() with its conjugates $\overline {s}$
with its conjugates $\overline {s}$![]() and $s', s''$
and $s', s''$![]() satisfying (7.5). Of course, then lemma 4.5 implies the density of the sumset (1.7) in ${\mathbb {C}}$
satisfying (7.5). Of course, then lemma 4.5 implies the density of the sumset (1.7) in ${\mathbb {C}}$![]() with
with
By (1.5), we have $\psi, \lambda \in E$![]() and so their conjugates $\psi ', \lambda '$
and so their conjugates $\psi ', \lambda '$![]() are also in the same real quadratic field $E$
are also in the same real quadratic field $E$![]() . Take a square-free integer $D>1$
. Take a square-free integer $D>1$![]() for which $E={\mathbb {Q}}(\sqrt {D})$
for which $E={\mathbb {Q}}(\sqrt {D})$![]() . Then, there are some rational numbers $\psi _1, \psi _2, \lambda _1, \lambda _2$
. Then, there are some rational numbers $\psi _1, \psi _2, \lambda _1, \lambda _2$![]() such that
such that
This implies
From the second inequality in (7.5), namely $\psi <\psi '$![]() , we obtain $\psi _2>0$
, we obtain $\psi _2>0$![]() . Likewise, from the third inequality in (7.5), $\lambda > \lambda '$
. Likewise, from the third inequality in (7.5), $\lambda > \lambda '$![]() , it follows that $\lambda _2 > 0$
, it follows that $\lambda _2 > 0$![]() . Now, from $\lambda '>0$
. Now, from $\lambda '>0$![]() we obtain $\lambda _1>\lambda _2 \sqrt {D}>0$
we obtain $\lambda _1>\lambda _2 \sqrt {D}>0$![]() . Consequently,
. Consequently,
Let $L$![]() be the least positive integer for which
be the least positive integer for which
Consider two cases, $\psi _1 \leq 0$![]() and $\psi _1 > 0$
and $\psi _1 > 0$![]() . In the first case, $\psi _1 \leq 0$
. In the first case, $\psi _1 \leq 0$![]() , from
, from
it follows that
Hence, by (7.8), (7.9) and $-\psi _1 \geq 0$![]() , the negative irrational number $-\sqrt {D}$
, the negative irrational number $-\sqrt {D}$![]() is a quotient of two elements of ${\mathbb {N}}[s]$
is a quotient of two elements of ${\mathbb {N}}[s]$![]() , i.e. $s_1=Ls^3+L(-\psi _1)s^2+L\lambda _1 s$
, i.e. $s_1=Ls^3+L(-\psi _1)s^2+L\lambda _1 s$![]() and $s_2=L\psi _2 s^2+L \lambda _2 s$
and $s_2=L\psi _2 s^2+L \lambda _2 s$![]() . Now, lemma 4.5 implies that the corresponding sumset of four sets (1.7) with the choice (7.6) is everywhere dense in ${\mathbb {C}}$
. Now, lemma 4.5 implies that the corresponding sumset of four sets (1.7) with the choice (7.6) is everywhere dense in ${\mathbb {C}}$![]() .
.
In the second case, $\psi _1>0$![]() , a key observation is the following identity:
, a key observation is the following identity:

Here, the second equality can be verified directly using $s^2+\lambda =\psi s$![]() and (7.7):
and (7.7):

Now, multiplying numerator and denominator by the factor $L^2\psi _2 s$![]() , we derive that
, we derive that
By (7.8), (7.9) and $\psi _1>0$![]() , we conclude that $\psi$
, we conclude that $\psi$![]() is a quotient of two nonzero elements of ${\mathbb {N}}[s]$
is a quotient of two nonzero elements of ${\mathbb {N}}[s]$![]() . Note that, by the first inequality in (7.5), $\psi$
. Note that, by the first inequality in (7.5), $\psi$![]() is negative, whereas, by $\psi _2>0$
is negative, whereas, by $\psi _2>0$![]() , it is irrational. Therefore, lemma 4.5 again implies that the sumset of four sets (1.7) with the choice (7.6) is everywhere dense in ${\mathbb {C}}$
, it is irrational. Therefore, lemma 4.5 again implies that the sumset of four sets (1.7) with the choice (7.6) is everywhere dense in ${\mathbb {C}}$![]() . This completes the proof of the last part of theorem 1.5.
. This completes the proof of the last part of theorem 1.5.