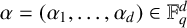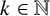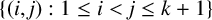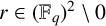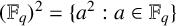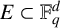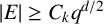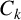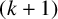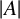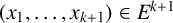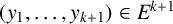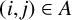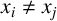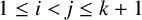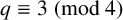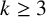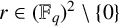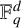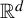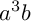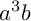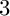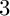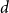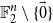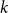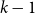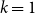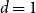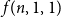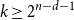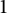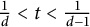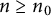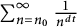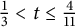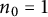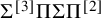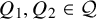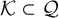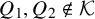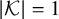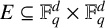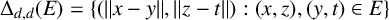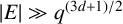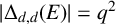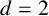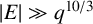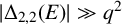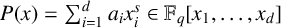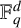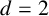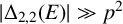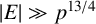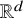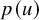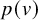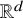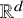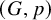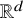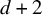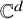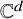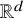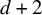133 results in 52Cxx
Indistinguishable asymptotic pairs and multidimensional Sturmian configurations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 31 May 2024, pp. 1-59
-
- Article
-
- You have access
- HTML
- Export citation
Complexity of non-abelian cut-and-project sets of polytopal type I: special homogeneous Lie groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1-43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometric structures in pseudo-random graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 March 2024, pp. 1-31
-
- Article
- Export citation
Sharp bounds for a discrete John’s theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 05 March 2024, pp. 1-3
-
- Article
- Export citation
Shi arrangements and low elements in affine Coxeter groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 12 February 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On restricted Falconer distance sets
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 05 February 2024, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NEAR OPTIMAL THRESHOLDS FOR EXISTENCE OF DILATED CONFIGURATIONS IN
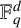 $\mathbb {F}_q^d$
$\mathbb {F}_q^d$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 26 January 2024, pp. 1-12
-
- Article
- Export citation
Stellahedral geometry of matroids
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 09 October 2023, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral cocycle for substitution tilings
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 18 September 2023, pp. 1629-1672
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TILINGS OF THE SPHERE BY CONGRUENT QUADRILATERALS II: EDGE COMBINATION
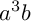 $a^3b$ WITH RATIONAL ANGLES
$a^3b$ WITH RATIONAL ANGLES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 07 September 2023, pp. 128-163
- Print publication:
- March 2024
-
- Article
- Export citation
Subspace coverings with multiplicities
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 18 May 2023, pp. 782-795
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fourier transformable measures with weak Meyer set support and their lift to the cut-and-project scheme
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 17 February 2023, pp. 1044-1060
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Perfectly packing a cube by cubes of nearly harmonic sidelength
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 14 February 2023, pp. 1061-1071
- Print publication:
- September 2023
-
- Article
- Export citation
Model sets with Euclidean internal space
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 11 January 2023, pp. 3897-3922
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A generalized Sylvester–Gallai-type theorem for quadratic polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 15 December 2022, e112
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE TWO-PARAMETER ERDŐS–FALCONER DISTANCE PROBLEM IN FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 29 September 2022, pp. 502-506
- Print publication:
- June 2023
-
- Article
- Export citation
ON 2-TRANSITIVE SETS OF EQUIANGULAR LINES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 22 August 2022, pp. 134-145
- Print publication:
- February 2023
-
- Article
- Export citation
Enriques surfaces and an Apollonian packing in eight dimensions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 11 July 2022, pp. 205-221
- Print publication:
- January 2023
-
- Article
- Export citation
Globally rigid graphs are fully reconstructible
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 07 July 2022, e51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tropical moments of tropical Jacobians
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 24 May 2022, pp. 1045-1075
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation








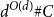
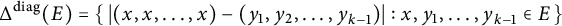
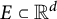
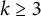
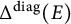
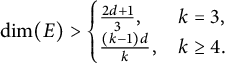
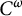
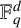
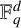
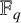
 for
for