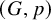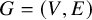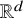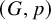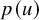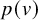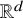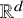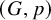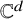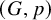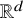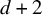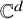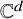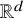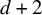1 Introduction
A (d-dimensional) framework is a pair ![]() $(G,p)$ where
$(G,p)$ where ![]() $G = (V,E)$ is a graph and
$G = (V,E)$ is a graph and ![]() $p : V \rightarrow \mathbb {R}^d$ is a map that assigns a point in
$p : V \rightarrow \mathbb {R}^d$ is a map that assigns a point in ![]() $\mathbb {R}^{d}$ to each vertex of G. The length of an edge
$\mathbb {R}^{d}$ to each vertex of G. The length of an edge ![]() $uv$ in
$uv$ in ![]() $(G,p)$ is the Euclidean distance between
$(G,p)$ is the Euclidean distance between ![]() $p(u)$ and
$p(u)$ and ![]() $p(v)$. We also call
$p(v)$. We also call ![]() $(G,p)$ a realization of G in
$(G,p)$ a realization of G in ![]() $\mathbb {R}^{d}$. The framework is generic if the set of the coordinates of its points is algebraically independent over
$\mathbb {R}^{d}$. The framework is generic if the set of the coordinates of its points is algebraically independent over ![]() $\mathbb {Q}$. We say that a d-dimensional framework
$\mathbb {Q}$. We say that a d-dimensional framework ![]() $(G,p)$ is globally rigid if every other realization
$(G,p)$ is globally rigid if every other realization ![]() $(G,q)$ of G in
$(G,q)$ of G in ![]() $\mathbb {R}^d$ in which corresponding edges have the same length is congruent to
$\mathbb {R}^d$ in which corresponding edges have the same length is congruent to ![]() $(G,p)$. That is, the graph G and its edge lengths in
$(G,p)$. That is, the graph G and its edge lengths in ![]() $(G,p)$ uniquely determine the pairwise distances of all vertices in
$(G,p)$ uniquely determine the pairwise distances of all vertices in ![]() $(G,p)$. It is known that for generic d-dimensional frameworks, global rigidity depends only on the graph G for all
$(G,p)$. It is known that for generic d-dimensional frameworks, global rigidity depends only on the graph G for all ![]() $d\geq 1$. We say that G is (generically) globally rigid in
$d\geq 1$. We say that G is (generically) globally rigid in ![]() $\mathbb {R}^d$ if every (equivalently, if some) generic realization of G in
$\mathbb {R}^d$ if every (equivalently, if some) generic realization of G in ![]() $\mathbb {R}^d$ is globally rigid. In the rest of this section, we give a brief overview of our main results. Most of the definitions and more details are given in the next section.
$\mathbb {R}^d$ is globally rigid. In the rest of this section, we give a brief overview of our main results. Most of the definitions and more details are given in the next section.
In the context of rigidity theory, unlabeled reconstruction is the study of what combinatorial and geometric information is determined by the (multi)set of edge lengths arising from some d-dimensional framework ![]() $(G,p)$. In [Reference Gortler, Theran and Thurston12], it was shown that if
$(G,p)$. In [Reference Gortler, Theran and Thurston12], it was shown that if ![]() $(G,p)$ is a generic globally rigid framework with n vertices in
$(G,p)$ is a generic globally rigid framework with n vertices in ![]() $\mathbb {R}^d$, where
$\mathbb {R}^d$, where ![]() $n \geq d+2$, then there can be no distinct (not necessarily generic) realization
$n \geq d+2$, then there can be no distinct (not necessarily generic) realization ![]() $(H,q)$ of any graph H with n vertices in
$(H,q)$ of any graph H with n vertices in ![]() $\mathbb {R}^d$ that produces the same edge lengths, up to trivialities. This result is essentially tight: If H is allowed to have more vertices or if G is not globally rigid, then p cannot be determined. To prove this result, it was sufficient to study the following, related graph reconstruction question.
$\mathbb {R}^d$ that produces the same edge lengths, up to trivialities. This result is essentially tight: If H is allowed to have more vertices or if G is not globally rigid, then p cannot be determined. To prove this result, it was sufficient to study the following, related graph reconstruction question.
We say that a graph G is strongly reconstructible in ![]() $\mathbb {C}^d$ if, whenever a pair of generic frameworks
$\mathbb {C}^d$ if, whenever a pair of generic frameworks ![]() $(G,p)$ and
$(G,p)$ and ![]() $(H,q)$ in
$(H,q)$ in ![]() $\mathbb {C}^d$ have the same set of edge lengths and the same number of vertices, we have that G is isomorphic to H and the corresponding edges have the same length. In [Reference Gortler, Theran and Thurston12], it was shown that, for
$\mathbb {C}^d$ have the same set of edge lengths and the same number of vertices, we have that G is isomorphic to H and the corresponding edges have the same length. In [Reference Gortler, Theran and Thurston12], it was shown that, for ![]() $d \geq 2$, globally rigid graphs in
$d \geq 2$, globally rigid graphs in ![]() $\mathbb {R}^d$ on at least
$\mathbb {R}^d$ on at least ![]() $d + 2$ vertices are strongly reconstructible in
$d + 2$ vertices are strongly reconstructible in ![]() $\mathbb {C}^d$. Although this result was sufficient to answer the original question of [Reference Gortler, Theran and Thurston12], as a pure reconstruction question, the dependence on n remains unsatisfying. To this end, we call a graph G fully reconstructible in
$\mathbb {C}^d$. Although this result was sufficient to answer the original question of [Reference Gortler, Theran and Thurston12], as a pure reconstruction question, the dependence on n remains unsatisfying. To this end, we call a graph G fully reconstructible in ![]() $\mathbb {C}^d$ if, whenever a pair of generic frameworks
$\mathbb {C}^d$ if, whenever a pair of generic frameworks ![]() $(G,p)$ and
$(G,p)$ and ![]() $(H,q)$ in
$(H,q)$ in ![]() $\mathbb {C}^d$ have the same set of edge lengths, but not necessarily the same number of vertices, we have that G is isomorphic to H and the corresponding edges have the same length. We stress that in the above definition we require both
$\mathbb {C}^d$ have the same set of edge lengths, but not necessarily the same number of vertices, we have that G is isomorphic to H and the corresponding edges have the same length. We stress that in the above definition we require both ![]() $(G,p)$ and
$(G,p)$ and ![]() $(H,q)$ to be generic. This, or some other nondegeneracy condition, is necessary since the edge lengths of
$(H,q)$ to be generic. This, or some other nondegeneracy condition, is necessary since the edge lengths of ![]() $(G,p)$ can be realized by an arbitrary forest H on
$(G,p)$ can be realized by an arbitrary forest H on ![]() $|E(G)|$ edges (but the realization
$|E(G)|$ edges (but the realization ![]() $(H,q)$ obtained in this way will usually be nongeneric).
$(H,q)$ obtained in this way will usually be nongeneric).
As we shall see, both strong reconstructibility and full reconstructibility can be (perhaps more naturally) stated as a uniqueness condition not on the generic realizations of G but rather on a certain complex variety associated to G. This variety, which we call the d-dimensional measurement variety of G and denote by ![]() $M_{d,G}$, is the Zariski-closure of the set of all vectors arising as the squared edge lengths of d-dimensional realizations of G. Roughly speaking, G is strongly reconstructible in
$M_{d,G}$, is the Zariski-closure of the set of all vectors arising as the squared edge lengths of d-dimensional realizations of G. Roughly speaking, G is strongly reconstructible in ![]() $\mathbb {C}^d$ if, whenever there is a bijection
$\mathbb {C}^d$ if, whenever there is a bijection ![]() $\psi : E(G) \rightarrow E(H)$ that sends
$\psi : E(G) \rightarrow E(H)$ that sends ![]() $M_{d,G}$ to
$M_{d,G}$ to ![]() $M_{d,H}$, where H has the same number of vertices as G, then G and H are isomorphic and
$M_{d,H}$, where H has the same number of vertices as G, then G and H are isomorphic and ![]() $\psi $ is consistent with an isomorphism between them (for detailed definitions see Subsection 2.6 and Theorem 2.19). Full reconstructibility has a similar characterization, with the only difference being that we do not require H to have the same number of vertices as G. Thus, strong reconstructibility in
$\psi $ is consistent with an isomorphism between them (for detailed definitions see Subsection 2.6 and Theorem 2.19). Full reconstructibility has a similar characterization, with the only difference being that we do not require H to have the same number of vertices as G. Thus, strong reconstructibility in ![]() $\mathbb {C}^d$ asserts that G, in a sense, is uniquely determined by
$\mathbb {C}^d$ asserts that G, in a sense, is uniquely determined by ![]() $n,d$ and
$n,d$ and ![]() $M_{d,G}$, while full reconstructibility means that G is uniquely determined by d and
$M_{d,G}$, while full reconstructibility means that G is uniquely determined by d and ![]() $M_{d,G}$.
$M_{d,G}$.
In [Reference Gortler, Theran and Thurston12], the question was posed whether global rigidity in ![]() $\mathbb {R}^d$ implies full reconstructibility in
$\mathbb {R}^d$ implies full reconstructibility in ![]() $\mathbb {C}^d$. For
$\mathbb {C}^d$. For ![]() $d=2$, the question was answered affirmatively in [Reference Garamvölgyi and Jordán8]. In this paper, as one of our main results, we substantially strengthen the previous results and show that, for all
$d=2$, the question was answered affirmatively in [Reference Garamvölgyi and Jordán8]. In this paper, as one of our main results, we substantially strengthen the previous results and show that, for all ![]() $d\geq 2$,
$d\geq 2$,
Results in [Reference Garamvölgyi and Jordán8] show that, for ![]() $d = 2$, this is tight: If a graph is not globally rigid in
$d = 2$, this is tight: If a graph is not globally rigid in ![]() $\mathbb {R}^2$, then it is not even strongly reconstructible in
$\mathbb {R}^2$, then it is not even strongly reconstructible in ![]() $\mathbb {C}^2$. The
$\mathbb {C}^2$. The ![]() $d=1$ case is slightly different but also fully characterizable using
$d=1$ case is slightly different but also fully characterizable using ![]() $3$-connectivity. For
$3$-connectivity. For ![]() $d \geq 3$, a characterization of full reconstructibility seems more elusive. In particular, we show that global rigidity in
$d \geq 3$, a characterization of full reconstructibility seems more elusive. In particular, we show that global rigidity in ![]() $\mathbb {R}^d$ is not necessary for full reconstructibility in
$\mathbb {R}^d$ is not necessary for full reconstructibility in ![]() $\mathbb {C}^d$. We also prove some positive and negative results regarding possible sufficient and possible necessary conditions for strong and full reconstructibility. These answer a number of questions that were posed in [Reference Gortler, Theran and Thurston12] and [Reference Garamvölgyi and Jordán8].
$\mathbb {C}^d$. We also prove some positive and negative results regarding possible sufficient and possible necessary conditions for strong and full reconstructibility. These answer a number of questions that were posed in [Reference Gortler, Theran and Thurston12] and [Reference Garamvölgyi and Jordán8].
To prove our result on full reconstructibility, we also prove a combinatorial theorem, interesting on its own right. We say that a graph is ![]() $\mathcal {R}_d$-connected if its d-dimensional (generic) rigidity matroid is connected (see the next section for detailed definitions). A combinatorial characterization of globally rigid graphs in
$\mathcal {R}_d$-connected if its d-dimensional (generic) rigidity matroid is connected (see the next section for detailed definitions). A combinatorial characterization of globally rigid graphs in ![]() $\mathbb {R}^d$ is known only for
$\mathbb {R}^d$ is known only for ![]() $d=1,2$ and is a major open problem for
$d=1,2$ and is a major open problem for ![]() $d\geq 3$. In higher dimensions, Hendrickson’s theorem (see Theorem 2.1) gives combinatorial necessary conditions that link global rigidity to connectivity and local rigidity properties of G. In this paper, as another main result, we strengthen one of Hendrickson’s necessary conditions (redundant rigidity) by proving that, for all
$d\geq 3$. In higher dimensions, Hendrickson’s theorem (see Theorem 2.1) gives combinatorial necessary conditions that link global rigidity to connectivity and local rigidity properties of G. In this paper, as another main result, we strengthen one of Hendrickson’s necessary conditions (redundant rigidity) by proving that, for all ![]() $d \geq 1$,
$d \geq 1$,
This result may lead to a better understanding of higher-dimensional global rigidity. In particular, we use it to find new examples of so-called H-graphs, graphs that satisfy Hendrickson’s conditions but are not globally rigid.
The rest of the paper is laid out as follows. In Section 2, we recall the definitions and results from rigidity theory and algebraic geometry that we shall use throughout the paper. Section 3 contains our main results: After making some structural observations about the measurement variety of graphs, we show that globally rigid graphs in ![]() $\mathbb {R}^d$ on at least
$\mathbb {R}^d$ on at least ![]() $d+2$ vertices are
$d+2$ vertices are ![]() $\mathcal {R}_d$-connected (Theorem 3.5) and, for
$\mathcal {R}_d$-connected (Theorem 3.5) and, for ![]() $d \geq 2$, fully reconstructible in
$d \geq 2$, fully reconstructible in ![]() $\mathbb {C}^d$ (Theorem 3.6). In Section 4, we illustrate the results of the previous section with several examples. In particular, we use Theorem 3.5 to give new examples of H-graphs. We also answer questions from [Reference Garamvölgyi and Jordán8] and [Reference Gortler, Theran and Thurston12] related to the unlabeled reconstructibility problem, as well as pose new open questions. Finally, in Section 5, we prove some new results regarding
$\mathbb {C}^d$ (Theorem 3.6). In Section 4, we illustrate the results of the previous section with several examples. In particular, we use Theorem 3.5 to give new examples of H-graphs. We also answer questions from [Reference Garamvölgyi and Jordán8] and [Reference Gortler, Theran and Thurston12] related to the unlabeled reconstructibility problem, as well as pose new open questions. Finally, in Section 5, we prove some new results regarding ![]() $\mathcal {R}_d$-connected graphs.
$\mathcal {R}_d$-connected graphs.
2 Preliminaries
We start by fixing some conventions. In the following, graphs will be understood to be simple, that is, without parallel edges and loops. To avoid some trivialities, we shall also implicitly assume that every graph considered has at least one edge (and thus at least two vertices). For a graph ![]() $G = (V,E)$, we shall use
$G = (V,E)$, we shall use ![]() $\mathbb {R}^E$ and
$\mathbb {R}^E$ and ![]() $\mathbb {C}^E$ to denote the
$\mathbb {C}^E$ to denote the ![]() $|E|$-dimensional real (complex, respectively) Euclidean space with axes labelled by the edges of G. We shall also often refer to the configuration spaces
$|E|$-dimensional real (complex, respectively) Euclidean space with axes labelled by the edges of G. We shall also often refer to the configuration spaces ![]() $\mathbb {R}^{nd}$ and
$\mathbb {R}^{nd}$ and ![]() $\mathbb {C}^{nd}$, where n denotes the number of vertices of G and
$\mathbb {C}^{nd}$, where n denotes the number of vertices of G and ![]() $d \geq 1$ is some dimension. We shall really think of these spaces as
$d \geq 1$ is some dimension. We shall really think of these spaces as ![]() $(\mathbb {R}^d)^V$ and
$(\mathbb {R}^d)^V$ and ![]() $(\mathbb {C}^d)^V$, i.e., as n-tuples of d-dimensional vectors, indexed by the vertices of G. Nonetheless, as it is less cumbersome, we shall use the notation
$(\mathbb {C}^d)^V$, i.e., as n-tuples of d-dimensional vectors, indexed by the vertices of G. Nonetheless, as it is less cumbersome, we shall use the notation ![]() $\mathbb {R}^{nd}$ and
$\mathbb {R}^{nd}$ and ![]() $\mathbb {C}^{nd}$.
$\mathbb {C}^{nd}$.
2.1 Real and complex frameworks
Let ![]() $G = (V,E)$ be a graph on n vertices and
$G = (V,E)$ be a graph on n vertices and ![]() $d \geq 1$ some fixed integer. A d-dimensional realization of G is a pair
$d \geq 1$ some fixed integer. A d-dimensional realization of G is a pair ![]() $(G,p)$, where
$(G,p)$, where ![]() $p : V \rightarrow \mathbb {R}^d$ maps the vertices of G into Euclidean space. We call such a map p (or equivalently, a point
$p : V \rightarrow \mathbb {R}^d$ maps the vertices of G into Euclidean space. We call such a map p (or equivalently, a point ![]() $p = (p_v)_{v \in V}$ in
$p = (p_v)_{v \in V}$ in ![]() $\mathbb {R}^{nd}$) a configuration, and we say that the pair
$\mathbb {R}^{nd}$) a configuration, and we say that the pair ![]() $(G,p)$ is a framework. Two d-dimensional frameworks
$(G,p)$ is a framework. Two d-dimensional frameworks ![]() $(G,p)$ and
$(G,p)$ and ![]() $(G,q)$ are equivalent if
$(G,q)$ are equivalent if ![]() $\left \lVert p(u) - p(v)\right \rVert = \left \lVert q(u) - q(v)\right \rVert $ for every edge
$\left \lVert p(u) - p(v)\right \rVert = \left \lVert q(u) - q(v)\right \rVert $ for every edge ![]() $uv \in E$ and congruent if the same holds for every pair of vertices
$uv \in E$ and congruent if the same holds for every pair of vertices ![]() $u,v \in V$. Here,
$u,v \in V$. Here, ![]() $\left \lVert \cdot \right \rVert $ denotes the Euclidean norm.
$\left \lVert \cdot \right \rVert $ denotes the Euclidean norm.
A framework is (locally) rigid if every continuous motion of the vertices which preserves the edge lengths takes it to a congruent framework and globally rigid if every equivalent framework is congruent to it.
We say that a configuration ![]() $p \in \mathbb {R}^{nd}$ is generic if its
$p \in \mathbb {R}^{nd}$ is generic if its ![]() $n \cdot d$ coordinates are algebraically independent over
$n \cdot d$ coordinates are algebraically independent over ![]() $\mathbb {Q}$. It is known that, in any fixed dimension d, both local and global rigidity are generic properties of the underlying graph, in the sense that either every generic d-dimensional framework is locally/globally rigid or none of them are (see [Reference Connelly5, Reference Gortler, Healy and Thurston10]). Thus, we say that a graph is rigid (respectively, globally rigid) in d dimensions if every (or equivalently, if some) generic d-dimensional realization of the graph is rigid (respectively, globally rigid).
$\mathbb {Q}$. It is known that, in any fixed dimension d, both local and global rigidity are generic properties of the underlying graph, in the sense that either every generic d-dimensional framework is locally/globally rigid or none of them are (see [Reference Connelly5, Reference Gortler, Healy and Thurston10]). Thus, we say that a graph is rigid (respectively, globally rigid) in d dimensions if every (or equivalently, if some) generic d-dimensional realization of the graph is rigid (respectively, globally rigid).
Let ![]() $G = (V,E)$ be a graph on n vertices and
$G = (V,E)$ be a graph on n vertices and ![]() $d \geq 1$. The function
$d \geq 1$. The function ![]() $m_{d,G} : \mathbb {R}^{nd} \rightarrow \mathbb {R}^E$ mapping each realization of G to the sequence of its Euclidean squared edge lengths is called the rigidity map or edge measurement map of G in d dimensions. That is, for a d-dimensional realization
$m_{d,G} : \mathbb {R}^{nd} \rightarrow \mathbb {R}^E$ mapping each realization of G to the sequence of its Euclidean squared edge lengths is called the rigidity map or edge measurement map of G in d dimensions. That is, for a d-dimensional realization ![]() $(G,p)$ of G, the coordinate of
$(G,p)$ of G, the coordinate of ![]() $m_{d,G}(p)$ corresponding to the edge
$m_{d,G}(p)$ corresponding to the edge ![]() $uv \in E$ is
$uv \in E$ is ![]() $\left \lVert p(u) - p(v)\right \rVert ^2$.
$\left \lVert p(u) - p(v)\right \rVert ^2$.
Analogously to the real case, we define a d-dimensional complex framework to be a pair ![]() $(G,p)$, where
$(G,p)$, where ![]() $G = (V,E)$ is a graph and
$G = (V,E)$ is a graph and ![]() $p : V \rightarrow \mathbb {C}^d$ is a complex mapping. Given a framework
$p : V \rightarrow \mathbb {C}^d$ is a complex mapping. Given a framework ![]() $(G,p)$ in
$(G,p)$ in ![]() $\mathbb {C}^d$ and a pair of vertices
$\mathbb {C}^d$ and a pair of vertices ![]() $u,v$ in G, we define the complex squared distance of u and v in
$u,v$ in G, we define the complex squared distance of u and v in ![]() $(G,p)$ by
$(G,p)$ by
 $$ \begin{align*} m_{uv}(p) = \left(p(u) - p(v)\right)^{T} \cdot \left(p(u) - p(v)\right) = \sum_{k=1}^d (p(u)_k - p(v)_k)^2, \end{align*} $$
$$ \begin{align*} m_{uv}(p) = \left(p(u) - p(v)\right)^{T} \cdot \left(p(u) - p(v)\right) = \sum_{k=1}^d (p(u)_k - p(v)_k)^2, \end{align*} $$where k indexes over the d dimension-coordinates. Note that in this definition we do not use conjugation, and thus, this is not the usual distance of ![]() $p(u)$ and
$p(u)$ and ![]() $p(v)$. We also note that the mapping
$p(v)$. We also note that the mapping ![]() $m_{uv} : \mathbb {C}^{nd} \rightarrow \mathbb {C}$ depends on G and d, but since these will always be clear from the context, we shall omit them from our notation.
$m_{uv} : \mathbb {C}^{nd} \rightarrow \mathbb {C}$ depends on G and d, but since these will always be clear from the context, we shall omit them from our notation.
For an edge ![]() $e = uv$ of G, we say that
$e = uv$ of G, we say that ![]() $m_{uv}(p)$ is the complex squared length of the edge in
$m_{uv}(p)$ is the complex squared length of the edge in ![]() $(G,p)$. For real frameworks, this coincides with the usual (Euclidean) squared length, so we can extend
$(G,p)$. For real frameworks, this coincides with the usual (Euclidean) squared length, so we can extend ![]() $m_{d,G}$ to a
$m_{d,G}$ to a ![]() $\mathbb {C}^{nd} \rightarrow \mathbb {C}^E$ function by letting
$\mathbb {C}^{nd} \rightarrow \mathbb {C}^E$ function by letting
We say, as in the real case, that two frameworks ![]() $(G,p)$ and
$(G,p)$ and ![]() $(G,q)$ are equivalent if
$(G,q)$ are equivalent if ![]() $m_{d,G}(p) = m_{d,G}(q)$, and they are congruent if
$m_{d,G}(p) = m_{d,G}(q)$, and they are congruent if ![]() $m_{d,K_V}(p) = m_{d,K_V}(q)$, where
$m_{d,K_V}(p) = m_{d,K_V}(q)$, where ![]() $K_V$ is the complete graph on the vertex set V. A configuration
$K_V$ is the complete graph on the vertex set V. A configuration ![]() $p \in \mathbb {C}^{nd}$ is, again, generic, if the coordinates of p are algebraically independent over
$p \in \mathbb {C}^{nd}$ is, again, generic, if the coordinates of p are algebraically independent over ![]() $\mathbb {Q}$. A point
$\mathbb {Q}$. A point ![]() $p \in \mathbb {R}^{nd}$ is generic as a real configuration precisely if it is generic as a complex one.
$p \in \mathbb {R}^{nd}$ is generic as a real configuration precisely if it is generic as a complex one.
Although we will not explicitly need them, we note that one can define the analogues of rigidity and global rigidity for complex frameworks. It turns out that, as in the real case, the (global) rigidity of generic complex frameworks only depends on the underlying graph, and the corresponding graph property of being ‘(globally) rigid in ![]() $\mathbb {C}^d$’ is equivalent to being (globally) rigid in
$\mathbb {C}^d$’ is equivalent to being (globally) rigid in ![]() $\mathbb {R}^d$; see [Reference Gortler and Thurston11, Reference Gortler, Theran and Thurston12].
$\mathbb {R}^d$; see [Reference Gortler and Thurston11, Reference Gortler, Theran and Thurston12].
It follows from the definitions that globally rigid graphs are rigid. The following much stronger necessary conditions of global rigidity are due to Hendrickson [Reference Hendrickson13]. We say that a graph is redundantly rigid in a given dimension if it remains rigid after deleting any edge. A graph is k-connected for some ![]() $k \geq 2$ if it has at least
$k \geq 2$ if it has at least ![]() $k+1$ vertices and it remains connected after deleting any set of less than k vertices.
$k+1$ vertices and it remains connected after deleting any set of less than k vertices.
Theorem 2.1 [Reference Hendrickson13].
Let G be a graph on at least ![]() $d+2$ vertices for some
$d+2$ vertices for some ![]() $d \geq 1$. Suppose that G is globally rigid in
$d \geq 1$. Suppose that G is globally rigid in ![]() $\mathbb {R}^d$. Then G is
$\mathbb {R}^d$. Then G is ![]() $(d+1)$-connected and redundantly rigid in
$(d+1)$-connected and redundantly rigid in ![]() $\mathbb {R}^d$.
$\mathbb {R}^d$.
In ![]() $d = 1,2$ dimensions, the conditions of Theorem 2.1 are, in fact, sufficient for global rigidity [Reference Jackson and Jordán14]. This fails in the
$d = 1,2$ dimensions, the conditions of Theorem 2.1 are, in fact, sufficient for global rigidity [Reference Jackson and Jordán14]. This fails in the ![]() $d \geq 3$ case, and a combinatorial characterization of globally rigid graphs in these dimensions is a major open question.
$d \geq 3$ case, and a combinatorial characterization of globally rigid graphs in these dimensions is a major open question.
2.2 The rigidity matrix and the rigidity matroid
The rigidity matroid of a graph G is a matroid defined on the edge set of G which reflects the rigidity properties of all generic realizations of G. For a general introduction to matroid theory, we refer the reader to [Reference Oxley18]. Let ![]() $(G,p)$ be a realization of a graph
$(G,p)$ be a realization of a graph ![]() $G=(V,E)$ in
$G=(V,E)$ in ![]() $\mathbb {R}^d$. The rigidity matrix of the framework
$\mathbb {R}^d$. The rigidity matrix of the framework ![]() $(G,p)$ is the matrix
$(G,p)$ is the matrix ![]() $R(G,p)$ of size
$R(G,p)$ of size ![]() $|E|\times d|V|$, where, for each edge
$|E|\times d|V|$, where, for each edge ![]() $v_iv_j\in E$, in the row corresponding to
$v_iv_j\in E$, in the row corresponding to ![]() $v_iv_j$, the entries in the d columns corresponding to vertices
$v_iv_j$, the entries in the d columns corresponding to vertices ![]() $v_i$ and
$v_i$ and ![]() $v_j$ contain the d coordinates of
$v_j$ contain the d coordinates of ![]() $(p(v_i)-p(v_j))$ and
$(p(v_i)-p(v_j))$ and ![]() $(p(v_j)-p(v_i))$, respectively, and the remaining entries are zeros. In other words, it is
$(p(v_j)-p(v_i))$, respectively, and the remaining entries are zeros. In other words, it is ![]() $1/2$ times the Jacobian of the rigidity map
$1/2$ times the Jacobian of the rigidity map ![]() $m_{d,G}$. The rigidity matrix of
$m_{d,G}$. The rigidity matrix of ![]() $(G,p)$ defines the rigidity matroid of
$(G,p)$ defines the rigidity matroid of ![]() $(G,p)$ on the ground set E by linear independence of rows. It is known that any pair of generic frameworks
$(G,p)$ on the ground set E by linear independence of rows. It is known that any pair of generic frameworks ![]() $(G,p)$ and
$(G,p)$ and ![]() $(G,q)$ have the same rigidity matroid. We call this the d-dimensional rigidity matroid
$(G,q)$ have the same rigidity matroid. We call this the d-dimensional rigidity matroid ![]() ${\mathcal{R}}_d(G)=(E,r_d)$ of the graph G. We can define the rigidity matrix
${\mathcal{R}}_d(G)=(E,r_d)$ of the graph G. We can define the rigidity matrix ![]() $R(G,p)$ for complex frameworks in the same way as in the real case. This, again, allows us to define the rigidity matroid of the framework. It is not difficult to show that the rigidity matroid of a generic framework in
$R(G,p)$ for complex frameworks in the same way as in the real case. This, again, allows us to define the rigidity matroid of the framework. It is not difficult to show that the rigidity matroid of a generic framework in ![]() $\mathbb {C}^d$ is, again, the d-dimensional rigidity matroid
$\mathbb {C}^d$ is, again, the d-dimensional rigidity matroid ![]() $\mathcal {R}_d(G)$.
$\mathcal {R}_d(G)$.
We denote the rank of ![]() ${\mathcal{R}}_d(G)$ by
${\mathcal{R}}_d(G)$ by ![]() $r_d(G)$. A graph
$r_d(G)$. A graph ![]() $G=(V,E)$ is
$G=(V,E)$ is ![]() $\mathcal {R}_d$-independent if
$\mathcal {R}_d$-independent if ![]() $r_d(G)=|E|$, and it is an
$r_d(G)=|E|$, and it is an ![]() $\mathcal {R}_d$-circuit if it is not
$\mathcal {R}_d$-circuit if it is not ![]() $\mathcal {R}_d$-independent, but every proper subgraph
$\mathcal {R}_d$-independent, but every proper subgraph ![]() $G'$ of G is
$G'$ of G is ![]() $\mathcal {R}_d$-independent. We note that in the literature such graphs are sometimes called M-independent in
$\mathcal {R}_d$-independent. We note that in the literature such graphs are sometimes called M-independent in ![]() $\mathbb {R}^d$ and M-circuits in
$\mathbb {R}^d$ and M-circuits in ![]() $\mathbb {R}^d$, respectively. An edge e of G is an
$\mathbb {R}^d$, respectively. An edge e of G is an ![]() $\mathcal {R}_d$-bridge in G if
$\mathcal {R}_d$-bridge in G if ![]() $r_d(G-e)=r_d(G)-1$ holds. Equivalently, e is an
$r_d(G-e)=r_d(G)-1$ holds. Equivalently, e is an ![]() $\mathcal {R}_d$-bridge in G if it is not contained in any subgraph of G that is an
$\mathcal {R}_d$-bridge in G if it is not contained in any subgraph of G that is an ![]() $\mathcal {R}_d$-circuit.
$\mathcal {R}_d$-circuit.
Gluck characterized rigid graphs in terms of their rank.
Theorem 2.2 [Reference Gluck9].
Let ![]() $G=(V,E)$ be a graph with
$G=(V,E)$ be a graph with ![]() $|V|\geq d+1$. Then G is rigid in
$|V|\geq d+1$. Then G is rigid in ![]() $\mathbb {R}^d$ if and only if
$\mathbb {R}^d$ if and only if ![]() $r_d(G)=d|V|-\binom {d+1}{2}$.
$r_d(G)=d|V|-\binom {d+1}{2}$.
Let ![]() ${\cal M}$ be a matroid on ground set E with rank function r. We can define a relation on the pairs of elements of E by saying that
${\cal M}$ be a matroid on ground set E with rank function r. We can define a relation on the pairs of elements of E by saying that ![]() $e,f\in E$ are equivalent if
$e,f\in E$ are equivalent if ![]() $e=f$ or there is a circuit C of
$e=f$ or there is a circuit C of ![]() ${\cal M}$ with
${\cal M}$ with ![]() $\{e,f\}\subseteq C$. This defines an equivalence relation. The equivalence classes are the connected components of
$\{e,f\}\subseteq C$. This defines an equivalence relation. The equivalence classes are the connected components of ![]() ${\cal M}$. The matroid is said to be connected if there is only one equivalence class and separable otherwise. We shall use the fact that
${\cal M}$. The matroid is said to be connected if there is only one equivalence class and separable otherwise. We shall use the fact that ![]() ${\cal M}$ is separable if and only if there is a partition
${\cal M}$ is separable if and only if there is a partition ![]() $E=E_1\cup E_2$ of E into two nonempty subsets for which
$E=E_1\cup E_2$ of E into two nonempty subsets for which
holds, where ![]() ${\cal M}_i$ denotes the restriction of
${\cal M}_i$ denotes the restriction of ![]() ${\cal M}$ to
${\cal M}$ to ![]() $E_i$,
$E_i$, ![]() $i=1,2$.
$i=1,2$.
Given a graph ![]() $G=(V,E)$, the subgraphs induced by the edge sets of the connected components of
$G=(V,E)$, the subgraphs induced by the edge sets of the connected components of ![]() ${\mathcal{R}}_d(G)$ are the
${\mathcal{R}}_d(G)$ are the ![]() $\mathcal {R}_d$-connected components of G. The graph is said to be
$\mathcal {R}_d$-connected components of G. The graph is said to be ![]() $\mathcal {R}_d$-connected if
$\mathcal {R}_d$-connected if ![]() ${\mathcal{R}}_d(G)$ is connected, and
${\mathcal{R}}_d(G)$ is connected, and ![]() $\mathcal {R}_d$-separable otherwise. See Figure 1 for an example of an
$\mathcal {R}_d$-separable otherwise. See Figure 1 for an example of an ![]() $\mathcal {R}_3$-separable graph.
$\mathcal {R}_3$-separable graph.

Figure 1 A ![]() $3$-connected, redundantly rigid and
$3$-connected, redundantly rigid and ![]() ${\mathcal{R}}_3$-separable graph. This graph satisfies
${\mathcal{R}}_3$-separable graph. This graph satisfies ![]() $r_3(G)= 36 = 27 + 9 =r_3(G^o)+r_3(K_5)$, where
$r_3(G)= 36 = 27 + 9 =r_3(G^o)+r_3(K_5)$, where ![]() $G^o$ is the outer ring of
$G^o$ is the outer ring of ![]() $K_5$’s and
$K_5$’s and ![]() $K_5$ is the subgraph induced by the black (filled) vertices.
$K_5$ is the subgraph induced by the black (filled) vertices.
In one and two dimensions, ![]() $\mathcal {R}_d$-connectivity has close ties with (global) rigidity, as shown by the following result.
$\mathcal {R}_d$-connectivity has close ties with (global) rigidity, as shown by the following result.
Theorem 2.3 [Reference Jackson and Jordán14].
Let G be a graph without isolated vertices and ![]() $d \in \{1,2\}$. Then
$d \in \{1,2\}$. Then
1. If G is globally rigid in
 $\mathbb {R}^d$ on at least
$\mathbb {R}^d$ on at least  $d+2$ vertices, then it is
$d+2$ vertices, then it is  $\mathcal {R}_d$-connected.
$\mathcal {R}_d$-connected.2. If G is
 $\mathcal {R}_d$-connected, then it is redundantly rigid in
$\mathcal {R}_d$-connected, then it is redundantly rigid in  $\mathbb {R}^d$.
$\mathbb {R}^d$.
It is known that part (b) of Theorem 2.3 is not true in ![]() $d \geq 3$ dimensions. On the other hand, we shall show that part (a) remains valid in d dimensions for all
$d \geq 3$ dimensions. On the other hand, we shall show that part (a) remains valid in d dimensions for all ![]() $d \geq 3$ (Theorem 3.5). We note that this is essentially a strengthening of the second part of Hendrickson’s theorem (Theorem 2.1), which can be seen as follows. A graph is redundantly rigid in
$d \geq 3$ (Theorem 3.5). We note that this is essentially a strengthening of the second part of Hendrickson’s theorem (Theorem 2.1), which can be seen as follows. A graph is redundantly rigid in ![]() $\mathbb {R}^d$ if and only if it is rigid in
$\mathbb {R}^d$ if and only if it is rigid in ![]() $\mathbb {R}^d$ and contains no
$\mathbb {R}^d$ and contains no ![]() $\mathcal {R}_d$-bridges, and
$\mathcal {R}_d$-bridges, and ![]() $\mathcal {R}_d$-connected graphs contain no
$\mathcal {R}_d$-connected graphs contain no ![]() $\mathcal {R}_d$-bridges (indeed, e is an
$\mathcal {R}_d$-bridges (indeed, e is an ![]() $\mathcal {R}_d$-bridge in G if and only if
$\mathcal {R}_d$-bridge in G if and only if ![]() $\{e\}$ is an
$\{e\}$ is an ![]() $\mathcal {R}_d$-connected component of G). Since a globally rigid graph is clearly rigid, Theorem 3.5 implies that such a graph (on at least
$\mathcal {R}_d$-connected component of G). Since a globally rigid graph is clearly rigid, Theorem 3.5 implies that such a graph (on at least ![]() $d+2$ vertices) is redundantly rigid as well.
$d+2$ vertices) is redundantly rigid as well.
Let ![]() $G = (V,E)$ be a graph on n vertices and
$G = (V,E)$ be a graph on n vertices and ![]() $(G,p)$ a framework in
$(G,p)$ a framework in ![]() $\mathbb {C}^d$. The elements of
$\mathbb {C}^d$. The elements of ![]() $\ker (R(G,p)) \subseteq \mathbb {C}^{nd}$ are the infinitesimal motions of
$\ker (R(G,p)) \subseteq \mathbb {C}^{nd}$ are the infinitesimal motions of ![]() $(G,p)$, while the elements of
$(G,p)$, while the elements of ![]() $\ker (R(G,p)^T) \subseteq \mathbb {C}^E$ are the equilibrium stresses (or stresses, for short) of
$\ker (R(G,p)^T) \subseteq \mathbb {C}^E$ are the equilibrium stresses (or stresses, for short) of ![]() $(G,p)$. We shall also use the notation
$(G,p)$. We shall also use the notation ![]() $S(G,p) = \ker (R(G,p)^T)$. Let us denote the column space of
$S(G,p) = \ker (R(G,p)^T)$. Let us denote the column space of ![]() $R(G,p)$ by
$R(G,p)$ by ![]() $\operatorname {\mathrm {span}}(R(G,p))$. By basic linear algebra,
$\operatorname {\mathrm {span}}(R(G,p))$. By basic linear algebra, ![]() $S(G,p)$ is the orthogonal complementFootnote 1 of
$S(G,p)$ is the orthogonal complementFootnote 1 of ![]() $\operatorname {\mathrm {span}}(R(G,p))$ in
$\operatorname {\mathrm {span}}(R(G,p))$ in ![]() $\mathbb {C}^E$. Since the elements of
$\mathbb {C}^E$. Since the elements of ![]() $S(G,p)$ capture the row dependences of
$S(G,p)$ capture the row dependences of ![]() $R(G,p)$, we have that G is
$R(G,p)$, we have that G is ![]() $\mathcal {R}_d$-independent if and only if for every generic realization
$\mathcal {R}_d$-independent if and only if for every generic realization ![]() $(G,p)$ in
$(G,p)$ in ![]() $\mathbb {C}^d$, we have
$\mathbb {C}^d$, we have ![]() $S(G,p) = \{0\}$, and G is an
$S(G,p) = \{0\}$, and G is an ![]() $\mathcal {R}_d$-circuit if and only if every generic realization
$\mathcal {R}_d$-circuit if and only if every generic realization ![]() $(G,p)$ in
$(G,p)$ in ![]() $\mathbb {C}^d$ has a unique (up to scalar multiple) nonzero equilibrium stress
$\mathbb {C}^d$ has a unique (up to scalar multiple) nonzero equilibrium stress ![]() $\omega $ and
$\omega $ and ![]() $\omega $ is nonzero on every edge of G.
$\omega $ is nonzero on every edge of G.
Suppose that G is ![]() $\mathcal {R}_d$-separable and let
$\mathcal {R}_d$-separable and let ![]() $E = E_1 \cup E_2$ be a partition of E into nonempty subsets such that for the graphs
$E = E_1 \cup E_2$ be a partition of E into nonempty subsets such that for the graphs ![]() $G_i$ induced by
$G_i$ induced by ![]() $E_i, i=1,2$, we have
$E_i, i=1,2$, we have ![]() $r_d(G) = r_d(G_1) + r_d(G_2)$. It is not difficult to see that, in this case for any generic realization
$r_d(G) = r_d(G_1) + r_d(G_2)$. It is not difficult to see that, in this case for any generic realization ![]() $(G,p)$ in
$(G,p)$ in ![]() $\mathbb {C}^d$, we have
$\mathbb {C}^d$, we have ![]() $\operatorname {\mathrm {span}}(R(G,p)) = \operatorname {\mathrm {span}}(R(G_1,p)) \oplus \operatorname {\mathrm {span}}(R(G_2,p))$ as linear subspaces of
$\operatorname {\mathrm {span}}(R(G,p)) = \operatorname {\mathrm {span}}(R(G_1,p)) \oplus \operatorname {\mathrm {span}}(R(G_2,p))$ as linear subspaces of ![]() $\mathbb {C}^E$, under the identification
$\mathbb {C}^E$, under the identification ![]() $\mathbb {C}^E = \mathbb {C}^{E_1} \times \mathbb {C}^{E_2}$. This also implies
$\mathbb {C}^E = \mathbb {C}^{E_1} \times \mathbb {C}^{E_2}$. This also implies ![]() $S(G,p) = S(G_1,p) \oplus S(G_2,p)$ under the same identification.
$S(G,p) = S(G_1,p) \oplus S(G_2,p)$ under the same identification.
We close this section by recalling the well-known coning operation on a graph. Given a graph G, the cone of G is obtained by adding a new vertex v to G, along with new edges from v to every vertex of G. Coning provides a transfer between various rigidity properties in d and ![]() $d+1$ dimensions, as shown by the following results.
$d+1$ dimensions, as shown by the following results.
Theorem 2.4. Let ![]() $d \geq 1$, and let
$d \geq 1$, and let ![]() $G = (V,E)$ be a graph.
$G = (V,E)$ be a graph.
1. [Reference Whiteley22] G is rigid in
 $\mathbb {R}^d$ (
$\mathbb {R}^d$ ( $\mathcal {R}_d$-independent, respectively) if and only if the cone graph
$\mathcal {R}_d$-independent, respectively) if and only if the cone graph  $G^v$ is rigid in
$G^v$ is rigid in  $\mathbb {R}^{d+1}$ (
$\mathbb {R}^{d+1}$ ( $\mathcal {R}_{d+1}$-independent, respectively).
$\mathcal {R}_{d+1}$-independent, respectively).2. [Reference Connelly and Whiteley6] G is globally rigid in
 $\mathbb {R}^d$ if and only if the cone graph
$\mathbb {R}^d$ if and only if the cone graph  $G^v$ is globally rigid in
$G^v$ is globally rigid in  $\mathbb {R}^{d+1}$.
$\mathbb {R}^{d+1}$.
2.3 Affine maps and conics at infinity
We say that a framework ![]() $(G,p)$ in
$(G,p)$ in ![]() $\mathbb {C}^d$ has full affine span if the affine span of the image of the vertices under p is all of
$\mathbb {C}^d$ has full affine span if the affine span of the image of the vertices under p is all of ![]() $\mathbb {C}^d$. A configuration
$\mathbb {C}^d$. A configuration ![]() $q \in \mathbb {C}^{nd}$, viewed as a point
$q \in \mathbb {C}^{nd}$, viewed as a point ![]() $q = (q_v)_{v \in V}$, is an affine image of p if
$q = (q_v)_{v \in V}$, is an affine image of p if ![]() $q_v = Ap_v + b, v \in V$ for some matrix
$q_v = Ap_v + b, v \in V$ for some matrix ![]() $A \in \mathbb {C}^{d \times d}$ and vector
$A \in \mathbb {C}^{d \times d}$ and vector ![]() $b \in \mathbb {C}^d$. We say that p and q are strongly congruent if q can be obtained as the affine image of p under a rigid motion, i.e., an affine map
$b \in \mathbb {C}^d$. We say that p and q are strongly congruent if q can be obtained as the affine image of p under a rigid motion, i.e., an affine map ![]() $x \mapsto Ax + b$ such that
$x \mapsto Ax + b$ such that ![]() $A^TA$ is the identity matrix.
$A^TA$ is the identity matrix.
Two frameworks ![]() $(G,p)$ and
$(G,p)$ and ![]() $(G,q)$ in
$(G,q)$ in ![]() $\mathbb {R}^d$ are strongly congruent if and only if they are congruent. This is not always the case for frameworks in
$\mathbb {R}^d$ are strongly congruent if and only if they are congruent. This is not always the case for frameworks in ![]() $\mathbb {C}^d$. However, congruent frameworks that have full affine span are strongly congruent; see [Reference Gortler and Thurston11, Corollary 8].
$\mathbb {C}^d$. However, congruent frameworks that have full affine span are strongly congruent; see [Reference Gortler and Thurston11, Corollary 8].
Let ![]() $(G,p)$ be a framework in
$(G,p)$ be a framework in ![]() $\mathbb {C}^d$. We say that the edge directions of
$\mathbb {C}^d$. We say that the edge directions of ![]() $(G,p)$ lie on a conic at infinity if there is a nonzero symmetric matrix Q such that, for every edge
$(G,p)$ lie on a conic at infinity if there is a nonzero symmetric matrix Q such that, for every edge ![]() $uv$ of G,
$uv$ of G, ![]() $(p(u) - p(v))^T Q (p(u) - p(v)) = 0$. The following lemma is implied by results of Connelly (see, e.g., [Reference Connelly5, Proposition 4.2]). For completeness, we give a proof.
$(p(u) - p(v))^T Q (p(u) - p(v)) = 0$. The following lemma is implied by results of Connelly (see, e.g., [Reference Connelly5, Proposition 4.2]). For completeness, we give a proof.
Lemma 2.5. Let ![]() $G = (V,E)$ be a graph and
$G = (V,E)$ be a graph and ![]() $(G,p)$ a framework in
$(G,p)$ a framework in ![]() $\mathbb {C}^d$ such that its edge directions do not lie on a conic at infinity. Let
$\mathbb {C}^d$ such that its edge directions do not lie on a conic at infinity. Let ![]() $(G,q)$ be a framework such that q is an affine image of p. Then
$(G,q)$ be a framework such that q is an affine image of p. Then ![]() $m_{d,G}(q) = m_{d,G}(p)$ if and only if q and p are congruent.
$m_{d,G}(q) = m_{d,G}(p)$ if and only if q and p are congruent.
Proof. The ‘if’ direction is immediate. In the other direction, suppose that ![]() $m_{d,G}(q) = m_{d,G}(p)$. Let
$m_{d,G}(q) = m_{d,G}(p)$. Let ![]() $x \mapsto Ax + b$ be an affine transformation that sends p to q. It follows from the definitions that, for any pair of vertices
$x \mapsto Ax + b$ be an affine transformation that sends p to q. It follows from the definitions that, for any pair of vertices ![]() $u,v \in V$,
$u,v \in V$,
Therefore we have
By assumption, for every edge ![]() $uv \in E$, the left-hand side of equation (2.1) is zero. Since the edge directions of
$uv \in E$, the left-hand side of equation (2.1) is zero. Since the edge directions of ![]() $(G,p)$ do not lie on a conic at infinity, this implies
$(G,p)$ do not lie on a conic at infinity, this implies ![]() $A^TA - I= 0$ so that the left-hand side is zero for every pair of vertices
$A^TA - I= 0$ so that the left-hand side is zero for every pair of vertices ![]() $u,v \in V$, which is what we wanted to show.
$u,v \in V$, which is what we wanted to show.
The following lemma is stated in [Reference Connelly5] for frameworks in ![]() $\mathbb {R}^d$, but the same proof works for frameworks in
$\mathbb {R}^d$, but the same proof works for frameworks in ![]() $\mathbb {C}^d$.
$\mathbb {C}^d$.
Lemma 2.6 [Reference Connelly5, Proposition 4.3].
Let G be a graph in which each vertex has degree at least d. Then for every generic realization ![]() $(G,p)$ in
$(G,p)$ in ![]() $\mathbb {C}^d$, the edge directions of
$\mathbb {C}^d$, the edge directions of ![]() $(G,p)$ do not lie on a conic at infinity.
$(G,p)$ do not lie on a conic at infinity.
The following lemma is folklore.
Lemma 2.7. Let ![]() $(G,p), (G,q)$ be frameworks in
$(G,p), (G,q)$ be frameworks in ![]() $\mathbb {C}^d$ and suppose that q is an affine image of p. Then
$\mathbb {C}^d$ and suppose that q is an affine image of p. Then ![]() $S(G,p) \subseteq S(G,q)$. If both
$S(G,p) \subseteq S(G,q)$. If both ![]() $(G,p)$ and
$(G,p)$ and ![]() $(G,q)$ have full affine span, then
$(G,q)$ have full affine span, then ![]() $S(G,p) = S(G,q)$.
$S(G,p) = S(G,q)$.
Proof. Let ![]() $x \mapsto Ax + b$ be the affine transformation that maps p to q, and let
$x \mapsto Ax + b$ be the affine transformation that maps p to q, and let ![]() $A'$ be the
$A'$ be the ![]() $nd \times nd$ block matrix with n copies of A in its diagonal and zeroes elsewhere, where n denotes the number of vertices of G. In other words,
$nd \times nd$ block matrix with n copies of A in its diagonal and zeroes elsewhere, where n denotes the number of vertices of G. In other words, ![]() $A'$ is the Kronecker product
$A'$ is the Kronecker product ![]() $I_n \otimes A$ of the
$I_n \otimes A$ of the ![]() $n \times n$ identity matrix and A.
$n \times n$ identity matrix and A.
Direct calculation shows that ![]() $R(G,q) = R(G,p)A'$, which immediately implies
$R(G,q) = R(G,p)A'$, which immediately implies ![]() $S(G,p) = \ker (R(G,p)^T) \subseteq \ker (R(G,q)^T) = S(G,q)$. If
$S(G,p) = \ker (R(G,p)^T) \subseteq \ker (R(G,q)^T) = S(G,q)$. If ![]() $(G,p)$ and
$(G,p)$ and ![]() $(G,q)$ have full affine span, then the affine map sending p to q must necessarily be invertible so that p is an affine image of q as well, implying
$(G,q)$ have full affine span, then the affine map sending p to q must necessarily be invertible so that p is an affine image of q as well, implying ![]() $S(G,q) \subseteq S(G,p)$.
$S(G,q) \subseteq S(G,p)$.
Finally, we shall use the following property of globally rigid graphs which is easy to deduce from previous results on global rigidity and maximum rank stress matrices. We sketch the proof and refer the reader to [Reference Connelly5, Reference Gortler, Healy and Thurston10] for the definitions and key theorems.
Theorem 2.8. Let G be a globally rigid graph on ![]() $n\geq d+2$ vertices in
$n\geq d+2$ vertices in ![]() $\mathbb {R}^d$, for some
$\mathbb {R}^d$, for some ![]() $d\geq 1$ and
$d\geq 1$ and ![]() $(G,p)$ a generic realization of G in
$(G,p)$ a generic realization of G in ![]() $\mathbb {C}^d$. For every realization
$\mathbb {C}^d$. For every realization ![]() $(G,q)$ in
$(G,q)$ in ![]() $\mathbb {C}^d$ with
$\mathbb {C}^d$ with ![]() $S(G,p) = S(G,q)$, we must have that q is an affine image of p.
$S(G,p) = S(G,q)$, we must have that q is an affine image of p.
Proof. Let ![]() $(G,p_0)$ be a generic realization of G in
$(G,p_0)$ be a generic realization of G in ![]() $\mathbb {R}^d$. It was shown in [Reference Gortler, Healy and Thurston10] that there exists an equilibrium stress
$\mathbb {R}^d$. It was shown in [Reference Gortler, Healy and Thurston10] that there exists an equilibrium stress ![]() $\omega _0$ for
$\omega _0$ for ![]() $(G,p_0)$ for which the associated stress matrix has rank
$(G,p_0)$ for which the associated stress matrix has rank ![]() $n-d-1$. The complex version of [Reference Gortler, Healy and Thurston10, Lemma 5.8] then implies that
$n-d-1$. The complex version of [Reference Gortler, Healy and Thurston10, Lemma 5.8] then implies that ![]() $(G,p)$ has an equilibrium stress
$(G,p)$ has an equilibrium stress ![]() $\omega $ such that the associated stress matrix has rank
$\omega $ such that the associated stress matrix has rank ![]() $n - d - 1$.
$n - d - 1$.
If ![]() $S(G,p) = S(G,q)$ for some realization
$S(G,p) = S(G,q)$ for some realization ![]() $(G,q)$, then
$(G,q)$, then ![]() $\omega $ is a stress for
$\omega $ is a stress for ![]() $(G,q)$ as well. Then (the complex version of) [Reference Connelly5, Proposition 1.2] implies that q is an affine image of p.
$(G,q)$ as well. Then (the complex version of) [Reference Connelly5, Proposition 1.2] implies that q is an affine image of p.
2.4 Algebraic geometry background
We briefly recall the notions from algebraic geometry that we shall use. For a more detailed exposition, see [Reference Gortler, Theran and Thurston12, Appendix A] or [Reference Garamvölgyi and Jordán8, Section 2.2]. We say that a subset ![]() $X \subseteq \mathbb {C}^m$ is a variety if it is the set of simultaneous vanishing points of some polynomials
$X \subseteq \mathbb {C}^m$ is a variety if it is the set of simultaneous vanishing points of some polynomials ![]() $f_1,\ldots ,f_k \in \mathbb {C}[x_1,\ldots ,x_m]$. The varieties in
$f_1,\ldots ,f_k \in \mathbb {C}[x_1,\ldots ,x_m]$. The varieties in ![]() $\mathbb {C}^m$ form the closed sets of the so-called Zariski topology. For an arbitrary set
$\mathbb {C}^m$ form the closed sets of the so-called Zariski topology. For an arbitrary set ![]() $X \subseteq \mathbb {C}^m$, we shall use
$X \subseteq \mathbb {C}^m$, we shall use ![]() $\overline {X}$ to denote its closure in the Zariski topology on
$\overline {X}$ to denote its closure in the Zariski topology on ![]() $\mathbb {C}^m$.
$\mathbb {C}^m$.
Let ![]() $X \subseteq \mathbb {C}^m$ be a variety. We denote by
$X \subseteq \mathbb {C}^m$ be a variety. We denote by ![]() $I(X) \subseteq \mathbb {C}[x_1,\ldots ,x_m]$ the set of polynomials that vanish on X. We say that X is irreducible if it cannot be written as the proper union of a finite number of varieties, and it is defined over
$I(X) \subseteq \mathbb {C}[x_1,\ldots ,x_m]$ the set of polynomials that vanish on X. We say that X is irreducible if it cannot be written as the proper union of a finite number of varieties, and it is defined over ![]() $\mathbb {Q}$ if
$\mathbb {Q}$ if ![]() $I(X)$ has a generating set consisting of polynomials with rational coefficients. The dimension of an irreducible variety X is the largest number k such that there exists a chain
$I(X)$ has a generating set consisting of polynomials with rational coefficients. The dimension of an irreducible variety X is the largest number k such that there exists a chain ![]() $X_0 \subsetneq X_1 \subsetneq \cdots \subsetneq X_k = X$ of irreducible varieties. From this definition, the following useful fact is immediate: If
$X_0 \subsetneq X_1 \subsetneq \cdots \subsetneq X_k = X$ of irreducible varieties. From this definition, the following useful fact is immediate: If ![]() $X,Y \subseteq \mathbb {C}^m$ are irreducible varieties of the same dimension with
$X,Y \subseteq \mathbb {C}^m$ are irreducible varieties of the same dimension with ![]() $X \subseteq Y$, then
$X \subseteq Y$, then ![]() $X = Y$. We shall also use the following result.
$X = Y$. We shall also use the following result.
Theorem 2.9 [Reference Shafarevich21, Chapter 3, Theorem 1.6 and Chapter 6, Example 1.33].
Let ![]() $X \subseteq \mathbb {C}^{m_1},Y \subseteq \mathbb {C}^{m_2}$ irreducible varieties. Then the Cartesian product
$X \subseteq \mathbb {C}^{m_1},Y \subseteq \mathbb {C}^{m_2}$ irreducible varieties. Then the Cartesian product ![]() $X \times Y \subseteq \mathbb {C}^{m_1 + m_2}$ is an irreducible variety of dimension
$X \times Y \subseteq \mathbb {C}^{m_1 + m_2}$ is an irreducible variety of dimension ![]() $\dim (X) + \dim (Y)$.
$\dim (X) + \dim (Y)$.
Let ![]() $X \subseteq \mathbb {C}^m$ be an irreducible variety. At each point
$X \subseteq \mathbb {C}^m$ be an irreducible variety. At each point ![]() $x \in X$, we define the Zariski tangent space of X at x, denoted by
$x \in X$, we define the Zariski tangent space of X at x, denoted by ![]() $T_x X$, to be the kernel of the Jacobian matrix of a set of generating polynomials of
$T_x X$, to be the kernel of the Jacobian matrix of a set of generating polynomials of ![]() $I(X)$, evaluated at x. Thus,
$I(X)$, evaluated at x. Thus, ![]() $T_x X$ is a linear subspace of
$T_x X$ is a linear subspace of ![]() $\mathbb {C}^m$. We say that x is smooth if
$\mathbb {C}^m$. We say that x is smooth if ![]() $\dim (T_x X) = \dim (X)$. If X is homogeneous (i.e., it can be defined by homogeneous polynomials, or equivalently,
$\dim (T_x X) = \dim (X)$. If X is homogeneous (i.e., it can be defined by homogeneous polynomials, or equivalently, ![]() $tx \in X$ for every
$tx \in X$ for every ![]() $x \in X$ and
$x \in X$ and ![]() $t \in \mathbb {C}$) and
$t \in \mathbb {C}$) and ![]() $x \in X$ is a smooth point, we define the Gauss fiber corresponding to x to be the set
$x \in X$ is a smooth point, we define the Gauss fiber corresponding to x to be the set ![]() $\{y \in X: y \text { is smooth and } T_y X = T_x X\}$.Footnote 2
$\{y \in X: y \text { is smooth and } T_y X = T_x X\}$.Footnote 2
Let ![]() $X \subseteq \mathbb {C}^m$ be a variety defined over
$X \subseteq \mathbb {C}^m$ be a variety defined over ![]() $\mathbb {Q}$. We say that a point
$\mathbb {Q}$. We say that a point ![]() $x \in X$ is generic in X if the only polynomials with rational coefficients satisfied by x are those in
$x \in X$ is generic in X if the only polynomials with rational coefficients satisfied by x are those in ![]() $I(X)$. Note that a framework
$I(X)$. Note that a framework ![]() $(G,p)$ in
$(G,p)$ in ![]() $\mathbb {C}^d$ is generic if and only if p is generic as a point of the variety
$\mathbb {C}^d$ is generic if and only if p is generic as a point of the variety ![]() $\mathbb {C}^{nd}$. If X is an irreducible variety defined over
$\mathbb {C}^{nd}$. If X is an irreducible variety defined over ![]() $\mathbb {Q}$, then every generic point of X is smooth. We shall also need the following result.
$\mathbb {Q}$, then every generic point of X is smooth. We shall also need the following result.
Lemma 2.10 [Reference Gortler, Theran and Thurston12, Lemma A.6].
Let ![]() $X \subseteq Y$ be irreducible varieties, with Y defined over
$X \subseteq Y$ be irreducible varieties, with Y defined over ![]() $\mathbb {Q}$. Suppose that X has at least one point which is generic in Y. Then the points in X which are generic in Y are Zariski-dense in X.
$\mathbb {Q}$. Suppose that X has at least one point which is generic in Y. Then the points in X which are generic in Y are Zariski-dense in X.
2.5 The measurement variety
Recall that for a graph ![]() $G = (V,E)$, we denote its d-dimensional edge measurement map by
$G = (V,E)$, we denote its d-dimensional edge measurement map by ![]() $m_{d,G} : \mathbb {C}^{nd} \rightarrow \mathbb {C}^E$.
$m_{d,G} : \mathbb {C}^{nd} \rightarrow \mathbb {C}^E$.
Definition 2.11. The d-dimensional measurement variety of a graph G (on n vertices), denoted by ![]() $M_{d,G}$, is the Zariski-closure of
$M_{d,G}$, is the Zariski-closure of ![]() $m_{d,G}(\mathbb {C}^{nd})$.
$m_{d,G}(\mathbb {C}^{nd})$.
We shall frequently use the following lemma on generic points. It follows by applying [Reference Gortler, Theran and Thurston12, Lemmas 4.4, A.7, A.8] to the varieties ![]() $\mathbb {C}^{nd}$,
$\mathbb {C}^{nd}$, ![]() $M_{d,G}$ and the map
$M_{d,G}$ and the map ![]() $m_{d,G}$.
$m_{d,G}$.
Lemma 2.12. Let ![]() $x\in M_{d,G}$ be a point in the measurement variety of G. Then x is generic in
$x\in M_{d,G}$ be a point in the measurement variety of G. Then x is generic in ![]() $M_{d,G}$ if and only if there is a generic point
$M_{d,G}$ if and only if there is a generic point ![]() $p\in \mathbb {C}^{nd}$ for which
$p\in \mathbb {C}^{nd}$ for which ![]() $x=m_{d,G}(p)$.
$x=m_{d,G}(p)$.
It is known that the measurement variety, being the Zariski-closure of the image of an irreducible variety defined over ![]() $\mathbb {Q}$, is also an irreducible variety defined over
$\mathbb {Q}$, is also an irreducible variety defined over ![]() $\mathbb {Q}$. It follows from the definition and basic topological considerations that if
$\mathbb {Q}$. It follows from the definition and basic topological considerations that if ![]() $E' \subseteq E$ is a subset of edges inducing a subgraph
$E' \subseteq E$ is a subset of edges inducing a subgraph ![]() $G'$ of G, then
$G'$ of G, then ![]() $M_{d,G'} = \overline {\pi _{E'}(M_{d,G})}$, where
$M_{d,G'} = \overline {\pi _{E'}(M_{d,G})}$, where ![]() $\pi _{E'} : \mathbb {C}^E \rightarrow \mathbb {C}^{E'}$ is the projection onto the coordinate axes corresponding to
$\pi _{E'} : \mathbb {C}^E \rightarrow \mathbb {C}^{E'}$ is the projection onto the coordinate axes corresponding to ![]() $E'$; see [Reference Garamvölgyi and Jordán8, Lemma 3.8].
$E'$; see [Reference Garamvölgyi and Jordán8, Lemma 3.8].
In what follows, we shall frequently compare the measurement varieties of different graphs, say ![]() $G = (V,E)$ and
$G = (V,E)$ and ![]() $H = (V',E')$, that have the same number of edges. Since
$H = (V',E')$, that have the same number of edges. Since ![]() $M_{d,G}$ and
$M_{d,G}$ and ![]() $M_{d,H}$ lie in different ambient spaces, to compare them we must specify an identification between
$M_{d,H}$ lie in different ambient spaces, to compare them we must specify an identification between ![]() $\mathbb {C}^E$ and
$\mathbb {C}^E$ and ![]() $\mathbb {C}^{E'}$. To this end, we introduce the following notation. Let
$\mathbb {C}^{E'}$. To this end, we introduce the following notation. Let ![]() $\psi : E \rightarrow E'$ be a bijection between the edge sets of G and H. We write that
$\psi : E \rightarrow E'$ be a bijection between the edge sets of G and H. We write that ![]() $M_{d,G} =_\psi M_{d,H}$ if
$M_{d,G} =_\psi M_{d,H}$ if ![]() $\Psi (M_{d,G}) = M_{d,H}$, where
$\Psi (M_{d,G}) = M_{d,H}$, where ![]() $\Psi : \mathbb {C}^{E} \rightarrow \mathbb {C}^{E'}$ is the mapping induced by
$\Psi : \mathbb {C}^{E} \rightarrow \mathbb {C}^{E'}$ is the mapping induced by ![]() $\psi $ in the natural way. Similarly, we write
$\psi $ in the natural way. Similarly, we write ![]() $M_{d,G} \subseteq _\psi M_{d,H}$ if
$M_{d,G} \subseteq _\psi M_{d,H}$ if ![]() $\Psi (M_{d,G}) \subseteq M_{d,H}$.
$\Psi (M_{d,G}) \subseteq M_{d,H}$.
The following results show that ![]() $\mathcal {R}_d(G)$ is ‘encoded’ in the measurement variety in some sense. This has been observed before; see, e.g., [Reference Garamvölgyi and Jordán8, Reference Gortler, Theran and Thurston12, Reference Rosen, Sidman and Theran19]. Using the terminology of the latter paper, the situation can be summarized by saying that the algebraic matroid corresponding to the variety
$\mathcal {R}_d(G)$ is ‘encoded’ in the measurement variety in some sense. This has been observed before; see, e.g., [Reference Garamvölgyi and Jordán8, Reference Gortler, Theran and Thurston12, Reference Rosen, Sidman and Theran19]. Using the terminology of the latter paper, the situation can be summarized by saying that the algebraic matroid corresponding to the variety ![]() $M_{d,G}$ is
$M_{d,G}$ is ![]() $\mathcal {R}_d(G)$.
$\mathcal {R}_d(G)$.
Lemma 2.13. Let G be a graph on n vertices. Then
In particular, for ![]() $n \geq d+1$ we have
$n \geq d+1$ we have ![]() $\dim (M_{d,G}) \leq nd - \binom {d+1}{2}$ and equality holds if and only if G is rigid in
$\dim (M_{d,G}) \leq nd - \binom {d+1}{2}$ and equality holds if and only if G is rigid in ![]() $\mathbb {R}^d$. Moreover, G is
$\mathbb {R}^d$. Moreover, G is ![]() $\mathcal {R}_d$-independent if and only if
$\mathcal {R}_d$-independent if and only if ![]() $M_{d,G} = \mathbb {C}^E$.
$M_{d,G} = \mathbb {C}^E$.
Theorem 2.14. Let G and H be graphs with the same number of edges, and suppose that ![]() $M_{d,G} =_\psi M_{d,H}$ under some edge bijection
$M_{d,G} =_\psi M_{d,H}$ under some edge bijection ![]() $\psi : E(G) \rightarrow E(H)$. Then
$\psi : E(G) \rightarrow E(H)$. Then ![]() $\psi $ defines an isomorphism between
$\psi $ defines an isomorphism between ![]() $\mathcal {R}_d(G)$ and
$\mathcal {R}_d(G)$ and ![]() $\mathcal {R}_d(H)$.
$\mathcal {R}_d(H)$.
The following result shows that the measurement variety also encodes the space of stresses of generic frameworks. This follows from the fact that ![]() $S(G,p)$ is the orthogonal complement of
$S(G,p)$ is the orthogonal complement of ![]() $\operatorname {\mathrm {span}}(R(G,p))$ in
$\operatorname {\mathrm {span}}(R(G,p))$ in ![]() $\mathbb {C}^E$ using standard results in differential geometry; see [Reference Gortler, Healy and Thurston10, Lemma 2.21] or [Reference Gortler, Theran and Thurston12, Lemma 4.10].
$\mathbb {C}^E$ using standard results in differential geometry; see [Reference Gortler, Healy and Thurston10, Lemma 2.21] or [Reference Gortler, Theran and Thurston12, Lemma 4.10].
Lemma 2.15. Let G be a graph and ![]() $(G,p)$ a generic realization in
$(G,p)$ a generic realization in ![]() $\mathbb {C}^d$ for some
$\mathbb {C}^d$ for some ![]() $d \geq 1$. Let
$d \geq 1$. Let ![]() $x = m_{d,G}(p) \in M_{d,G}$. Then the space of stresses
$x = m_{d,G}(p) \in M_{d,G}$. Then the space of stresses ![]() $S(G,p)$ is the orthogonal complement of the tangent space
$S(G,p)$ is the orthogonal complement of the tangent space ![]() $T_x(M_{d,G})$ in
$T_x(M_{d,G})$ in ![]() $\mathbb {C}^E$.
$\mathbb {C}^E$.
The lemma implies that if ![]() $(G,p)$ and
$(G,p)$ and ![]() $(G,q)$ are generic frameworks in
$(G,q)$ are generic frameworks in ![]() $\mathbb {C}^d$, then
$\mathbb {C}^d$, then ![]() $S(G,p)\not = S(G,q)$ if and only if the Gauss fibers corresponding to
$S(G,p)\not = S(G,q)$ if and only if the Gauss fibers corresponding to ![]() $m_{d,G}(p)$ and
$m_{d,G}(p)$ and ![]() $m_{d,G}(q)$ are different. We shall use this corollary later.
$m_{d,G}(q)$ are different. We shall use this corollary later.
2.6 Unlabeled reconstruction
In what follows, it will be convenient to use the following notions. We say that two frameworks ![]() $(G,p)$ and
$(G,p)$ and ![]() $(H,q)$ in
$(H,q)$ in ![]() $\mathbb {C}^d$ are length-equivalent (under the bijection
$\mathbb {C}^d$ are length-equivalent (under the bijection ![]() $\psi $) if there is a bijection
$\psi $) if there is a bijection ![]() $\psi $ between the edge sets of G and H such that, for every edge e of G, the complex squared length of e in
$\psi $ between the edge sets of G and H such that, for every edge e of G, the complex squared length of e in ![]() $(G,p)$ is equal to the complex squared length of
$(G,p)$ is equal to the complex squared length of ![]() $\psi (e)$ in
$\psi (e)$ in ![]() $(H,q)$. For an edge bijection
$(H,q)$. For an edge bijection ![]() $\psi : E(G) \rightarrow E(H)$ and a graph isomorphism
$\psi : E(G) \rightarrow E(H)$ and a graph isomorphism ![]() $\varphi : V(G) \rightarrow V(H)$, we say that
$\varphi : V(G) \rightarrow V(H)$, we say that ![]() $\psi $ is induced by
$\psi $ is induced by ![]() $\varphi $ if for every edge
$\varphi $ if for every edge ![]() $e = uv \in E(G)$ we have
$e = uv \in E(G)$ we have ![]() $\psi (e) = \varphi (u)\varphi (v)$.
$\psi (e) = \varphi (u)\varphi (v)$.
Definition 2.16. Let ![]() $(G,p)$ be a generic realization of the graph G in
$(G,p)$ be a generic realization of the graph G in ![]() $\mathbb {C}^d$. We say that
$\mathbb {C}^d$. We say that ![]() $(G,p)$ is strongly reconstructible if for every generic framework
$(G,p)$ is strongly reconstructible if for every generic framework ![]() $(H,q)$ in
$(H,q)$ in ![]() $\mathbb {C}^d$ that is length-equivalent to
$\mathbb {C}^d$ that is length-equivalent to ![]() $(G,p)$ under some edge bijection
$(G,p)$ under some edge bijection ![]() $\psi : E(G) \rightarrow E(H)$, where H has the same number of vertices as G,
$\psi : E(G) \rightarrow E(H)$, where H has the same number of vertices as G, ![]() $\psi $ is induced by a graph isomorphism
$\psi $ is induced by a graph isomorphism ![]() $\varphi : V(G) \rightarrow V(H)$.
$\varphi : V(G) \rightarrow V(H)$.
In this paper, we shall mainly focus on the following stronger property, where the condition on the number of vertices of H is omitted.
Definition 2.17. Let G be a graph without isolated vertices, and let ![]() $(G,p)$ be a generic realization of G in
$(G,p)$ be a generic realization of G in ![]() $\mathbb {C}^d$. We say that
$\mathbb {C}^d$. We say that ![]() $(G,p)$ is fully reconstructible if, for every generic framework
$(G,p)$ is fully reconstructible if, for every generic framework ![]() $(H,q)$ in
$(H,q)$ in ![]() $\mathbb {C}^d$ that is length-equivalent to
$\mathbb {C}^d$ that is length-equivalent to ![]() $(G,p)$ under some edge bijection
$(G,p)$ under some edge bijection ![]() $\psi : E(G) \rightarrow E(H)$, where H has no isolated vertices,
$\psi : E(G) \rightarrow E(H)$, where H has no isolated vertices, ![]() $\psi $ is induced by a graph isomorphism
$\psi $ is induced by a graph isomorphism ![]() $\varphi : V(G) \rightarrow V(H)$.
$\varphi : V(G) \rightarrow V(H)$.
Note that, since we assume ![]() $(G,p)$ to be generic, its edge lengths are pairwise distinct, and hence, the bijection
$(G,p)$ to be generic, its edge lengths are pairwise distinct, and hence, the bijection ![]() $\psi $ is unique in the above definitions. We also point out that, when considering full reconstructibility, it is natural to only consider graphs without isolated vertices since from any framework we can create other length-equivalent frameworks by adding isolated vertices. On the other hand, in the case of strong reconstructibility it is sensible to consider graphs with isolated vertices. In fact, it follows immediately from the definitions that G is fully reconstructible in
$\psi $ is unique in the above definitions. We also point out that, when considering full reconstructibility, it is natural to only consider graphs without isolated vertices since from any framework we can create other length-equivalent frameworks by adding isolated vertices. On the other hand, in the case of strong reconstructibility it is sensible to consider graphs with isolated vertices. In fact, it follows immediately from the definitions that G is fully reconstructible in ![]() $\mathbb {C}^d$ if and only if every graph obtained from G by adding zero or more isolated vertices is strongly reconstructible in
$\mathbb {C}^d$ if and only if every graph obtained from G by adding zero or more isolated vertices is strongly reconstructible in ![]() $\mathbb {C}^d$.
$\mathbb {C}^d$.
As Theorem 2.19 below shows, both strong and full reconstructibility of a generic framework can be characterized in terms of a certain uniqueness condition on the measurement variety ![]() $M_{d,G}$ of the underlying graph, and in fact it is this formulation of reconstructibility that we shall most commonly use throughout the paper. This also implies that these reconstructibility notions are generic properties of a graph in the sense that if there is a generic framework
$M_{d,G}$ of the underlying graph, and in fact it is this formulation of reconstructibility that we shall most commonly use throughout the paper. This also implies that these reconstructibility notions are generic properties of a graph in the sense that if there is a generic framework ![]() $(G,p)$ in
$(G,p)$ in ![]() $\mathbb {C}^d$ which is strongly (respectively, fully) reconstructible, then every generic realization of G in
$\mathbb {C}^d$ which is strongly (respectively, fully) reconstructible, then every generic realization of G in ![]() $\mathbb {C}^d$ is strongly (respectively, fully) reconstructible. This motivates the following definition.
$\mathbb {C}^d$ is strongly (respectively, fully) reconstructible. This motivates the following definition.
Definition 2.18. A graph G is said to be (generically) strongly reconstructible (respectively, (generically) fully reconstructible) in ![]() $\mathbb {C}^d$ if every generic realization
$\mathbb {C}^d$ if every generic realization ![]() $(G,p)$ of G in
$(G,p)$ of G in ![]() $\mathbb {C}^d$ is strongly (respectively, fully) reconstructible.
$\mathbb {C}^d$ is strongly (respectively, fully) reconstructible.
Theorem 2.19. Let G be a graph and ![]() $d \geq 1$ be fixed. The following are equivalent.
$d \geq 1$ be fixed. The following are equivalent.
1. G is generically strongly reconstructible (generically fully reconstructible, respectively) in
 $\mathbb {C}^d$.
$\mathbb {C}^d$.2. There exists some generic framework
 $(G,p)$ in
$(G,p)$ in  $\mathbb {C}^d$ that is strongly reconstructible (fully reconstructible, respectively).
$\mathbb {C}^d$ that is strongly reconstructible (fully reconstructible, respectively).3. Whenever
 $M_{d,G} =_\psi M_{d,H}$ under an edge bijection
$M_{d,G} =_\psi M_{d,H}$ under an edge bijection  $\psi : E(G) \rightarrow E(H)$ for some graph H, where H has the same number of vertices as G (where H has an arbitrary number of vertices, respectively),
$\psi : E(G) \rightarrow E(H)$ for some graph H, where H has the same number of vertices as G (where H has an arbitrary number of vertices, respectively),  $\psi $ is induced by a graph isomorphism.
$\psi $ is induced by a graph isomorphism.
The ‘strongly reconstructible’ part of Theorem 2.19 is [Reference Garamvölgyi and Jordán8, Theorem 3.4]. The same proof works for the ‘fully reconstructible’ version after omitting the condition on the number of vertices of H.
We close this section by recalling the main result of [Reference Gortler, Theran and Thurston12].
Theorem 2.20 [Reference Gortler, Theran and Thurston12, Theorem 3.4].
Let G be a graph on at least ![]() $d+2$ vertices, where
$d+2$ vertices, where ![]() $d \geq 1$. Suppose that
$d \geq 1$. Suppose that
•
 $d = 1$ and G is
$d = 1$ and G is  $3$-connected, or
$3$-connected, or•
 $d \geq 2$ and G is globally rigid in
$d \geq 2$ and G is globally rigid in  $\mathbb {R}^d$.
$\mathbb {R}^d$.
Then G is strongly reconstructible in ![]() $\mathbb {C}^d$.
$\mathbb {C}^d$.
In the next section, we shall strengthen this result by proving that globally rigid graphs on at least ![]() $d+2$ vertices are, in fact, fully reconstructible in
$d+2$ vertices are, in fact, fully reconstructible in ![]() $\mathbb {C}^d$ for
$\mathbb {C}^d$ for ![]() $d\geq 2$. The cases
$d\geq 2$. The cases ![]() $d = 1,2$ were already settled in [Reference Garamvölgyi and Jordán8] by verifying the following equivalence.
$d = 1,2$ were already settled in [Reference Garamvölgyi and Jordán8] by verifying the following equivalence.
Theorem 2.21 [Reference Garamvölgyi and Jordán8, Theorem 5.19, Corollary 5.22, Theorem 5.1].
Let G be a graph on at least ![]() $d+2$ vertices and without isolated vertices, where
$d+2$ vertices and without isolated vertices, where ![]() $d \in \{1,2\}$. Then the following are equivalent.
$d \in \{1,2\}$. Then the following are equivalent.
•
 $d = 1$ and G is
$d = 1$ and G is  $3$-connected or
$3$-connected or  $d=2$ and G is globally rigid in
$d=2$ and G is globally rigid in  $\mathbb {R}^2$.
$\mathbb {R}^2$.• G is strongly reconstructible in
 $\mathbb {C}^d$.
$\mathbb {C}^d$.• G is fully reconstructible in
 $\mathbb {C}^d$.
$\mathbb {C}^d$.
In Section 4, we shall give examples showing that, for ![]() $d \geq 3$, there are fully reconstructible graphs in
$d \geq 3$, there are fully reconstructible graphs in ![]() $\mathbb {C}^d$ (on at least
$\mathbb {C}^d$ (on at least ![]() $d+2$ vertices) that are not globally rigid in
$d+2$ vertices) that are not globally rigid in ![]() $\mathbb {R}^d$. On the other hand, we do not know any example of a strongly reconstructible graph in
$\mathbb {R}^d$. On the other hand, we do not know any example of a strongly reconstructible graph in ![]() $\mathbb {C}^d$ on at least
$\mathbb {C}^d$ on at least ![]() $d+2$ vertices that is not fully reconstructible in
$d+2$ vertices that is not fully reconstructible in ![]() $\mathbb {C}^d$, although it seems likely that such a graph exists.
$\mathbb {C}^d$, although it seems likely that such a graph exists.
3 Necessary conditions for global rigidity
In this section, we prove our main results: Globally rigid graphs in ![]() $\mathbb {R}^d$ on at least
$\mathbb {R}^d$ on at least ![]() $d+2$ vertices are
$d+2$ vertices are ![]() $\mathcal {R}_d$-connected (Theorem 3.5) and fully reconstructible in
$\mathcal {R}_d$-connected (Theorem 3.5) and fully reconstructible in ![]() $\mathbb {C}^d$ (Theorem 3.6). We start with some technical results about the structure of the measurement variety that we shall use in these proofs. Apart from Lemma 3.1, the lemmas in the next subsection are implicit in [Reference Gortler, Theran and Thurston12].
$\mathbb {C}^d$ (Theorem 3.6). We start with some technical results about the structure of the measurement variety that we shall use in these proofs. Apart from Lemma 3.1, the lemmas in the next subsection are implicit in [Reference Gortler, Theran and Thurston12].
3.1 The structure of the measurement variety
The next lemma implies that the measurement variety of an ![]() $\mathcal {R}_d$-separable graph G is the product of the measurement varieties of its
$\mathcal {R}_d$-separable graph G is the product of the measurement varieties of its ![]() $\mathcal {R}_d$-connected components. A special case of this statement when G contains an
$\mathcal {R}_d$-connected components. A special case of this statement when G contains an ![]() $\mathcal {R}_d$-bridge was proved in [Reference Garamvölgyi and Jordán8, Theorem 3.13].
$\mathcal {R}_d$-bridge was proved in [Reference Garamvölgyi and Jordán8, Theorem 3.13].
Lemma 3.1. Let ![]() $d \geq 1$ and let
$d \geq 1$ and let ![]() $G = (V,E)$ be a graph. Suppose that there is a partition
$G = (V,E)$ be a graph. Suppose that there is a partition ![]() $E = E_1 \cup E_2$ of E into nonempty subsets such that
$E = E_1 \cup E_2$ of E into nonempty subsets such that ![]() $r_d(E) =r_d(E_1) + r_d(E_2)$. Let
$r_d(E) =r_d(E_1) + r_d(E_2)$. Let ![]() $G_1$ and
$G_1$ and ![]() $G_2$ be the subgraphs induced by
$G_2$ be the subgraphs induced by ![]() $E_1$ and
$E_1$ and ![]() $E_2$, respectively. Then
$E_2$, respectively. Then ![]() $M_{d,G} = M_{d,G_1} \times M_{d,G_2}$ (under the identification
$M_{d,G} = M_{d,G_1} \times M_{d,G_2}$ (under the identification ![]() $\mathbb {C}^E = \mathbb {C}^{E_1} \times \mathbb {C}^{E_2})$.
$\mathbb {C}^E = \mathbb {C}^{E_1} \times \mathbb {C}^{E_2})$.
Proof. For ![]() $i=1,2$,
$i=1,2$, ![]() $M_{d,G_i}$ arises as the Zariski-closure of the projection of
$M_{d,G_i}$ arises as the Zariski-closure of the projection of ![]() $M_{d,G}$ onto the coordinate axes corresponding to
$M_{d,G}$ onto the coordinate axes corresponding to ![]() $E_i$, so we have that
$E_i$, so we have that ![]() $M_{d,G} \subseteq M_{d,G_1} \times M_{d,G_2}$. By Theorem 2.9 and Lemma 2.13,
$M_{d,G} \subseteq M_{d,G_1} \times M_{d,G_2}$. By Theorem 2.9 and Lemma 2.13, ![]() $M_{d,G_1} \times M_{d,G_2}$ is an irreducible variety of dimension
$M_{d,G_1} \times M_{d,G_2}$ is an irreducible variety of dimension ![]() $r_d(E_1) + r_d(E_2)$. Since this dimension equals the dimension
$r_d(E_1) + r_d(E_2)$. Since this dimension equals the dimension ![]() $r_d(E)$ of the irreducible variety
$r_d(E)$ of the irreducible variety ![]() $M_{d,G}$, the two varieties must be equal.
$M_{d,G}$, the two varieties must be equal.
Lemma 3.2. Let G be a graph and ![]() $(G,p)$ a generic framework in
$(G,p)$ a generic framework in ![]() $\mathbb {C}^d$ with full affine span. Let
$\mathbb {C}^d$ with full affine span. Let ![]() $\mathcal {A} \subseteq \mathbb {C}^{nd}$ denote the set of affine images of p, and let
$\mathcal {A} \subseteq \mathbb {C}^{nd}$ denote the set of affine images of p, and let ![]() $F \subseteq M_{d,G}$ be the Gauss fiber corresponding to
$F \subseteq M_{d,G}$ be the Gauss fiber corresponding to ![]() $m_{d,G}(p)$. Then
$m_{d,G}(p)$. Then ![]() $\overline {m_{d,G}(\mathcal {A})} \subseteq \overline {F}$.
$\overline {m_{d,G}(\mathcal {A})} \subseteq \overline {F}$.
Proof. For clarity, we shall write m and M instead of ![]() $m_{d,G}$ and
$m_{d,G}$ and ![]() $M_{d,G}$ in the following. For any
$M_{d,G}$ in the following. For any ![]() $q \in \mathcal {A}$, if q has full affine span, then by Lemma 2.7, we have
$q \in \mathcal {A}$, if q has full affine span, then by Lemma 2.7, we have ![]() $S(G,p) = S(G,q)$.
$S(G,p) = S(G,q)$.
Let ![]() $\mathcal {A}^g$ denote the set of frameworks in
$\mathcal {A}^g$ denote the set of frameworks in ![]() $\mathcal {A}$ that are generic. Since
$\mathcal {A}$ that are generic. Since ![]() $(G,p)$ is generic, this set is nonempty, and since
$(G,p)$ is generic, this set is nonempty, and since ![]() $\mathcal {A}$ is irreducible (being a linear space), Lemma 2.10 implies
$\mathcal {A}$ is irreducible (being a linear space), Lemma 2.10 implies ![]() $\overline {\mathcal {A}^g} = \mathcal {A}$. Now for any
$\overline {\mathcal {A}^g} = \mathcal {A}$. Now for any ![]() $q \in \mathcal {A}^g$, we have
$q \in \mathcal {A}^g$, we have ![]() $S(G,q) = S(G,p)$ by Lemma 2.7, and it follows by Lemma 2.15 that
$S(G,q) = S(G,p)$ by Lemma 2.7, and it follows by Lemma 2.15 that ![]() $T_{m(q)} M = T_{m(p)} M$, or in other words,
$T_{m(q)} M = T_{m(p)} M$, or in other words, ![]() $m(q) \in F$.
$m(q) \in F$.
This shows that ![]() $m(\mathcal {A}^g) \subseteq F$. Taking Zariski-closures and using the continuity of m with respect to the Zariski topology, we have
$m(\mathcal {A}^g) \subseteq F$. Taking Zariski-closures and using the continuity of m with respect to the Zariski topology, we have
as desired.
Although we shall not use this fact, we note that, by [Reference Gortler, Theran and Thurston12, Lemma 4.6], ![]() $m_{d,G}(\mathcal {A})$ is a linear space, and in particular it is closed.
$m_{d,G}(\mathcal {A})$ is a linear space, and in particular it is closed.
Let G be a graph and ![]() $d \geq 1$. We say that a Gauss fiber F of
$d \geq 1$. We say that a Gauss fiber F of ![]() $M_{d,G}$ is generic if it contains a point that is generic in
$M_{d,G}$ is generic if it contains a point that is generic in ![]() $M_{d,G}$. It will also be convenient to use the following notion in the next proof. Let
$M_{d,G}$. It will also be convenient to use the following notion in the next proof. Let ![]() $d \geq 2$, and let n denote the number of vertices of G. We say that a framework
$d \geq 2$, and let n denote the number of vertices of G. We say that a framework ![]() $(G,p)$ in
$(G,p)$ in ![]() $\mathbb {C}^d$ is a lifting of the framework
$\mathbb {C}^d$ is a lifting of the framework ![]() $(G,q)$ in
$(G,q)$ in ![]() $\mathbb {C}^{d-1}$ if
$\mathbb {C}^{d-1}$ if ![]() $(G,q)$ is obtained by projecting the image of each vertex in
$(G,q)$ is obtained by projecting the image of each vertex in ![]() $(G,p)$ onto the first
$(G,p)$ onto the first ![]() $d-1$ coordinate axes. If
$d-1$ coordinate axes. If ![]() $(G,q)$ is generic, then the generic liftings of
$(G,q)$ is generic, then the generic liftings of ![]() $(G,q)$ form a dense subset of the space of liftings of
$(G,q)$ form a dense subset of the space of liftings of ![]() $(G,q)$. This follows from the basic fact that for any finite set
$(G,q)$. This follows from the basic fact that for any finite set ![]() $S \subseteq \mathbb {C}$ that is algebraically independent over
$S \subseteq \mathbb {C}$ that is algebraically independent over ![]() $\mathbb {Q}$, the numbers
$\mathbb {Q}$, the numbers ![]() $x \in \mathbb {C}$ for which
$x \in \mathbb {C}$ for which ![]() $S \cup \{x\}$ is also algebraically independent form a dense subset of
$S \cup \{x\}$ is also algebraically independent form a dense subset of ![]() $\mathbb {C}$.
$\mathbb {C}$.
Lemma 3.3. Let ![]() $G = (V,E)$ be a graph and
$G = (V,E)$ be a graph and ![]() $d \geq 2$.
$d \geq 2$.
1. If G is not
 $\mathcal {R}_d$-independent, then for every point
$\mathcal {R}_d$-independent, then for every point  $x \in M_{d-1,G} \subseteq M_{d,G}$ that is generic in
$x \in M_{d-1,G} \subseteq M_{d,G}$ that is generic in  $M_{d-1,G}$ there are an infinite number of generic Gauss fibers F of
$M_{d-1,G}$ there are an infinite number of generic Gauss fibers F of  $M_{d,G}$ with
$M_{d,G}$ with  $x \in \overline {F}$.
$x \in \overline {F}$.2. If G is globally rigid in
 $\mathbb {R}^d$ on at least
$\mathbb {R}^d$ on at least  $d+2$ vertices and
$d+2$ vertices and  $x \in M_{d,G} \setminus M_{d-1,G}$, then there are at most a finite number of generic Gauss fibers F of
$x \in M_{d,G} \setminus M_{d-1,G}$, then there are at most a finite number of generic Gauss fibers F of  $M_{d,G}$ with
$M_{d,G}$ with  $x \in \overline {F}$.
$x \in \overline {F}$.
Proof. a) [Following [Reference Gortler, Theran and Thurston12, Proposition 4.21]] For clarity, we shall write m instead of ![]() $m_{d,G}$ in the following. We note first that, since G is not
$m_{d,G}$ in the following. We note first that, since G is not ![]() $\mathcal {R}_d$-independent, it has at least
$\mathcal {R}_d$-independent, it has at least ![]() $d+2$ vertices and consequently any generic realization of G in
$d+2$ vertices and consequently any generic realization of G in ![]() $\mathbb {C}^d$ has full affine span.
$\mathbb {C}^d$ has full affine span.
Let ![]() $x \in M_{d-1,G}$ be a generic point. By Lemma 2.12, there is a generic framework
$x \in M_{d-1,G}$ be a generic point. By Lemma 2.12, there is a generic framework ![]() $(G,q)$ in
$(G,q)$ in ![]() $\mathbb {C}^{d-1}$ with
$\mathbb {C}^{d-1}$ with ![]() $m_{d-1,G}(q) = x$. It is enough to find an infinite sequence of generic frameworks
$m_{d-1,G}(q) = x$. It is enough to find an infinite sequence of generic frameworks ![]() $(G,p_i), i \in \mathbb {N}$ in
$(G,p_i), i \in \mathbb {N}$ in ![]() $\mathbb {C}^d$, with corresponding (generic) Gauss fibers
$\mathbb {C}^d$, with corresponding (generic) Gauss fibers ![]() $F_i, i \in \mathbb {N}$ such that
$F_i, i \in \mathbb {N}$ such that ![]() ${F}_i \neq {F}_j$ for
${F}_i \neq {F}_j$ for ![]() $i \neq j$ and such that q is an affine image of
$i \neq j$ and such that q is an affine image of ![]() $p_i$ since by Lemma 3.2 this implies
$p_i$ since by Lemma 3.2 this implies ![]() $x \in \overline {F}_i$.
$x \in \overline {F}_i$.
We shall find such frameworks ![]() $(G,p_i)$ inductively. In fact, each framework will be a lifting of
$(G,p_i)$ inductively. In fact, each framework will be a lifting of ![]() $(G,q)$. For the base case, let
$(G,q)$. For the base case, let ![]() $p_1$ be an arbitrary generic lifting of
$p_1$ be an arbitrary generic lifting of ![]() $(G,q)$. Now suppose that for some
$(G,q)$. Now suppose that for some ![]() $i> 1$, we have already found suitable frameworks
$i> 1$, we have already found suitable frameworks ![]() $(G,p_j), j < i$. Since G is not
$(G,p_j), j < i$. Since G is not ![]() $\mathcal {R}_d$-independent, each of these frameworks has a nonzero stress
$\mathcal {R}_d$-independent, each of these frameworks has a nonzero stress ![]() $\omega _j$. For a given lifting
$\omega _j$. For a given lifting ![]() $(G,p)$ of
$(G,p)$ of ![]() $(G,q)$ to have
$(G,q)$ to have ![]() $\omega _j$ as an equlibrium stress, the last coordinates
$\omega _j$ as an equlibrium stress, the last coordinates ![]() $p(v)_d, v \in V$ must satisfy
$p(v)_d, v \in V$ must satisfy ![]() $|V|$ linear equations determined by
$|V|$ linear equations determined by ![]() $\omega _j$, and since
$\omega _j$, and since ![]() $\omega _j$ is nonzero, some of these equations are nontrivial. It follows that, for each
$\omega _j$ is nonzero, some of these equations are nontrivial. It follows that, for each ![]() $j < i$, the liftings of
$j < i$, the liftings of ![]() $(G,q)$ that do not have
$(G,q)$ that do not have ![]() $\omega _j$ as an equilibrium stress form a dense open subset of the space of liftings of
$\omega _j$ as an equilibrium stress form a dense open subset of the space of liftings of ![]() $(G,q)$. This implies that we can find a generic lifting
$(G,q)$. This implies that we can find a generic lifting ![]() $(G,p_i)$ that does not satisfy any of the stresses
$(G,p_i)$ that does not satisfy any of the stresses ![]() $\omega _j, j < i$, and so in particular
$\omega _j, j < i$, and so in particular ![]() $S(G,p_i) \neq S(G,p_j)$ for
$S(G,p_i) \neq S(G,p_j)$ for ![]() $j < i$. Let
$j < i$. Let ![]() $F_i$ denote the Gauss fiber corresponding to
$F_i$ denote the Gauss fiber corresponding to ![]() $m(p_i)$. By Lemma 2.15, we must have
$m(p_i)$. By Lemma 2.15, we must have ![]() $T_{m(p_i)} M_{d,G} \neq T_{m(p_j)} M_{d,G}$, and hence
$T_{m(p_i)} M_{d,G} \neq T_{m(p_j)} M_{d,G}$, and hence ![]() $F_i \neq F_j$ for
$F_i \neq F_j$ for ![]() $j < i$.
$j < i$.
b) This is an immediate consequence of Proposition 4.20 and Remark 4.8 of [Reference Gortler, Theran and Thurston12].
Corollary 3.4. Let G be a globally rigid graph in ![]() $\mathbb {R}^d$ on at least
$\mathbb {R}^d$ on at least ![]() $d+2$ vertices for some
$d+2$ vertices for some ![]() $d \geq 2$, and suppose that
$d \geq 2$, and suppose that ![]() $M_{d,G} =_\psi M_{d,H}$ under some edge bijection
$M_{d,G} =_\psi M_{d,H}$ under some edge bijection ![]() $\psi $ for some graph H not necessarily on the same number of vertices as G. Then
$\psi $ for some graph H not necessarily on the same number of vertices as G. Then ![]() $M_{d-1,H} \subseteq _\psi M_{d-1,G}$.
$M_{d-1,H} \subseteq _\psi M_{d-1,G}$.
Proof. For clarity, we shall suppress the role of ![]() $\psi $ and assume that
$\psi $ and assume that ![]() $M_{d,G}$ and
$M_{d,G}$ and ![]() $M_{d,H}$ are in the same ambient space
$M_{d,H}$ are in the same ambient space ![]() $\mathbb {C}^E$ so that
$\mathbb {C}^E$ so that ![]() $M_{d,G} = M_{d,H}$. Let R be the ring of polynomials over
$M_{d,G} = M_{d,H}$. Let R be the ring of polynomials over ![]() $\mathbb {C}$ with variables indexed by E and let
$\mathbb {C}$ with variables indexed by E and let ![]() $I(M_{d-1,G}),I(M_{d-1,H}) \subseteq R$ be the set of polynomials vanishing on
$I(M_{d-1,G}),I(M_{d-1,H}) \subseteq R$ be the set of polynomials vanishing on ![]() $M_{d-1,G}$ and
$M_{d-1,G}$ and ![]() $M_{d-1,H}$, respectively. Moreover, let
$M_{d-1,H}$, respectively. Moreover, let ![]() $R_{\mathbb {Q}},I_{\mathbb {Q}}(M_{d-1,G})$ and
$R_{\mathbb {Q}},I_{\mathbb {Q}}(M_{d-1,G})$ and ![]() $I_{\mathbb {Q}}(M_{d-1,H})$ denote the subset of
$I_{\mathbb {Q}}(M_{d-1,H})$ denote the subset of ![]() $R,I(M_{d-1,G})$ and
$R,I(M_{d-1,G})$ and ![]() $I(M_{d-1,H})$, respectively, consisting of polynomials with rational coefficients.
$I(M_{d-1,H})$, respectively, consisting of polynomials with rational coefficients.
Theorem 2.1 implies that G has no ![]() $\mathcal {R}_d$-bridges, so in particular it cannot be
$\mathcal {R}_d$-bridges, so in particular it cannot be ![]() $\mathcal {R}_d$-independent. By Theorem 2.14, it follows that H is not
$\mathcal {R}_d$-independent. By Theorem 2.14, it follows that H is not ![]() $\mathcal {R}_d$-independent either, and thus, part a) of Lemma 3.3 implies that there is a generic point
$\mathcal {R}_d$-independent either, and thus, part a) of Lemma 3.3 implies that there is a generic point ![]() $x \in M_{d-1,H} \subseteq M_{d,H}$ such that there is an infinite number of generic Gauss fibers
$x \in M_{d-1,H} \subseteq M_{d,H}$ such that there is an infinite number of generic Gauss fibers ![]() $F \subseteq M_{d,H}$ with
$F \subseteq M_{d,H}$ with ![]() $x \in \overline {F}$. Part b) of the same lemma then implies that x is in
$x \in \overline {F}$. Part b) of the same lemma then implies that x is in ![]() $M_{d-1,G}$. From this and the fact that x is generic in
$M_{d-1,G}$. From this and the fact that x is generic in ![]() $M_{d-1,H}$, we have the following chain of containments:
$M_{d-1,H}$, we have the following chain of containments:
Since both ![]() $M_{d-1,G}$ and
$M_{d-1,G}$ and ![]() $M_{d-1,H}$ are defined over
$M_{d-1,H}$ are defined over ![]() $\mathbb {Q}$,
$\mathbb {Q}$, ![]() $I_{\mathbb {Q}}(M_{d-1,G})$ and
$I_{\mathbb {Q}}(M_{d-1,G})$ and ![]() $I_{\mathbb {Q}}(M_{d-1,H})$ generate
$I_{\mathbb {Q}}(M_{d-1,H})$ generate ![]() $I(M_{d-1,G})$ and
$I(M_{d-1,G})$ and ![]() $I(M_{d-1,H})$, respectively. Thus, equation (3.1) also implies
$I(M_{d-1,H})$, respectively. Thus, equation (3.1) also implies ![]() $I(M_{d-1,G}) \subseteq I(M_{d-1,H})$, which is equivalent to
$I(M_{d-1,G}) \subseteq I(M_{d-1,H})$, which is equivalent to ![]() $M_{d-1,H} \subseteq M_{d-1,G}$.
$M_{d-1,H} \subseteq M_{d-1,G}$.
3.2 Globally rigid graphs are  $\mathcal {R}_d$-connected
$\mathcal {R}_d$-connected
We are ready to prove the first main result of this section.
Theorem 3.5. Let ![]() $G = (V,E)$ be a globally rigid graph in
$G = (V,E)$ be a globally rigid graph in ![]() $\mathbb {R}^d$ on
$\mathbb {R}^d$ on ![]() $n\geq d+2$ vertices. Then G is
$n\geq d+2$ vertices. Then G is ![]() $\mathcal {R}_d$-connected.
$\mathcal {R}_d$-connected.
Proof. Let ![]() $(G,p)$ be a generic framework in
$(G,p)$ be a generic framework in ![]() $\mathbb {C}^d$. We shall show that if G is not
$\mathbb {C}^d$. We shall show that if G is not ![]() $\mathcal {R}_d$-connected, then there is a framework
$\mathcal {R}_d$-connected, then there is a framework ![]() $(G,q)$ in
$(G,q)$ in ![]() $\mathbb {C}^d$ such that
$\mathbb {C}^d$ such that ![]() $S(G,p) = S(G,q)$ but where q is not an affine image of p. Then, from Theorem 2.8, G cannot be globally rigid in
$S(G,p) = S(G,q)$ but where q is not an affine image of p. Then, from Theorem 2.8, G cannot be globally rigid in ![]() $\mathbb {R}^d$, and we are done.
$\mathbb {R}^d$, and we are done.
If G is not ![]() $\mathcal {R}_d$-connected, there must be a partition
$\mathcal {R}_d$-connected, there must be a partition ![]() $E = E_1 \cup E_2$ of E into nonempty subsets with
$E = E_1 \cup E_2$ of E into nonempty subsets with ![]() $r_d(E) = r_d(E_1) + r_d(E_2)$. Let
$r_d(E) = r_d(E_1) + r_d(E_2)$. Let ![]() $G_1 = (V,E_1)$ and
$G_1 = (V,E_1)$ and ![]() $G_2 = (V,E_2)$, and let
$G_2 = (V,E_2)$, and let ![]() $(G_1,p), (G_2,p)$ denote the respective subframeworks of
$(G_1,p), (G_2,p)$ denote the respective subframeworks of ![]() $(G,p)$.
$(G,p)$.
By Theorem 2.1, G contains no ![]() $\mathcal {R}_d$-bridges, that is, every edge is contained in an
$\mathcal {R}_d$-bridges, that is, every edge is contained in an ![]() $\mathcal {R}_d$-circuit. Since any
$\mathcal {R}_d$-circuit. Since any ![]() $\mathcal {R}_d$-circuit that contains edges from
$\mathcal {R}_d$-circuit that contains edges from ![]() $E_1$ must be contained in
$E_1$ must be contained in ![]() $G_1$, we have that
$G_1$, we have that ![]() $G_1$ contains an
$G_1$ contains an ![]() $\mathcal {R}_d$-circuit, so in particular it has a subgraph of minimum degree at least
$\mathcal {R}_d$-circuit, so in particular it has a subgraph of minimum degree at least ![]() $d + 1$. Thus, by Lemma 2.6, applied to this subgraph, the edge directions of
$d + 1$. Thus, by Lemma 2.6, applied to this subgraph, the edge directions of ![]() $(G_1,p)$ do not lie on a conic at infinity.
$(G_1,p)$ do not lie on a conic at infinity.
Now we find our promised ![]() $(G,q)$. By Lemma 3.1,
$(G,q)$. By Lemma 3.1, ![]() $M_{d,G} = M_{d,G_1} \times M_{d,G_2}$. Let
$M_{d,G} = M_{d,G_1} \times M_{d,G_2}$. Let ![]() $m_{d,G}(p) = (x_1,x_2) \in M_{d,G}$. Now
$m_{d,G}(p) = (x_1,x_2) \in M_{d,G}$. Now ![]() $x_2 \in M_{d,G_2}$ implies
$x_2 \in M_{d,G_2}$ implies ![]() $4x_2 \in M_{d,G_2}$ and consequently
$4x_2 \in M_{d,G_2}$ and consequently ![]() $(x_1,4x_2) \in M_{d,G}$. Since
$(x_1,4x_2) \in M_{d,G}$. Since ![]() $(G,p)$ was generic,
$(G,p)$ was generic, ![]() $(x_1,x_2)$ is generic in
$(x_1,x_2)$ is generic in ![]() $M_{d,G}$ by Lemma 2.12, and this implies that
$M_{d,G}$ by Lemma 2.12, and this implies that ![]() $(x_1,4x_2)$ is generic in
$(x_1,4x_2)$ is generic in ![]() $M_{d,G}$ as well. Using Lemma 2.12, it follows that there is a generic framework
$M_{d,G}$ as well. Using Lemma 2.12, it follows that there is a generic framework ![]() $(G,q)$ in
$(G,q)$ in ![]() $\mathbb {C}^d$ with
$\mathbb {C}^d$ with ![]() $m_{d,G}(q) = (x_1,4x_2)$.
$m_{d,G}(q) = (x_1,4x_2)$.
Let us consider the subframeworks ![]() $(G_1,q)$ and
$(G_1,q)$ and ![]() $(G_2,q)$. Both of these frameworks are generic. Also note that
$(G_2,q)$. Both of these frameworks are generic. Also note that ![]() $(G_1,q)$ is equivalent to
$(G_1,q)$ is equivalent to ![]() $(G_1,p)$ and
$(G_1,p)$ and ![]() $(G_2,q)$ is equivalent to
$(G_2,q)$ is equivalent to ![]() $(G_2,2p)$. Since
$(G_2,2p)$. Since ![]() $S(G,p) = S(G,2p)$, this implies
$S(G,p) = S(G,2p)$, this implies ![]() $S(G,p) = S(G_1,p) \oplus S(G_2,p) = S(G_1,q) \oplus S(G_2,q) = S(G,q)$, as desired.
$S(G,p) = S(G_1,p) \oplus S(G_2,p) = S(G_1,q) \oplus S(G_2,q) = S(G,q)$, as desired.
We have that ![]() $(G_1,q)$ is equivalent to
$(G_1,q)$ is equivalent to ![]() $(G_1,p)$. As established above, the edge directions of
$(G_1,p)$. As established above, the edge directions of ![]() $(G_1,p)$ do not lie on a conic at infinity. Thus, it follows from Lemma 2.5 that if q is an affine image of p, then q must be congruent to p. But q is clearly not congruent to p as
$(G_1,p)$ do not lie on a conic at infinity. Thus, it follows from Lemma 2.5 that if q is an affine image of p, then q must be congruent to p. But q is clearly not congruent to p as ![]() $(G_2,p)$ is not equivalent to
$(G_2,p)$ is not equivalent to ![]() $(G_2,q)$. Thus, p is not an affine image of q, as desired.
$(G_2,q)$. Thus, p is not an affine image of q, as desired.
Theorem 3.5 was known to hold in ![]() $\mathbb {R}^1$ (where global rigidity,
$\mathbb {R}^1$ (where global rigidity, ![]() $2$-connectivity and
$2$-connectivity and ![]() $\mathcal {R}_1$-connectivity are equivalent) and in
$\mathcal {R}_1$-connectivity are equivalent) and in ![]() $\mathbb {R}^2$, see [Reference Jackson and Jordán14] (c.f. Theorem 2.3 above). We note that in [Reference Jordán and Tanigawa17] it is conjectured that globally rigid graphs are ‘nondegenerate’ in
$\mathbb {R}^2$, see [Reference Jackson and Jordán14] (c.f. Theorem 2.3 above). We note that in [Reference Jordán and Tanigawa17] it is conjectured that globally rigid graphs are ‘nondegenerate’ in ![]() $\mathbb {R}^d$, a condition that is stronger than
$\mathbb {R}^d$, a condition that is stronger than ![]() $\mathcal {R}_d$-connectivity.
$\mathcal {R}_d$-connectivity.
Underlying the proof of Theorem 3.5 is the following structural observation on the measurement variety of G, which we give without details. Since G is globally rigid, [Reference Gortler, Healy and Thurston10, Theorem 4.4] and [Reference Gortler, Theran and Thurston12, Lemma 4.24, Remark 4.25] imply that for any generic Gauss fiber F of ![]() $M_{d,G}$ we have
$M_{d,G}$ we have ![]() $\dim (\overline {F}) = \binom {d+1}{2}$. On the other hand, it follows from the definitions that if
$\dim (\overline {F}) = \binom {d+1}{2}$. On the other hand, it follows from the definitions that if ![]() $M_{d,G} = M_{d,G_1} \times M_{d,G_2}$, then
$M_{d,G} = M_{d,G_1} \times M_{d,G_2}$, then ![]() $F = F_1 \times F_2$, where
$F = F_1 \times F_2$, where ![]() $F_1$ and
$F_1$ and ![]() $F_2$ are some generic Gauss fibers of
$F_2$ are some generic Gauss fibers of ![]() $M_{d,G_1}$ and
$M_{d,G_1}$ and ![]() $M_{d,G_2}$, respectively. Using Lemma 3.2, it can be shown that, under the assumptions on
$M_{d,G_2}$, respectively. Using Lemma 3.2, it can be shown that, under the assumptions on ![]() $G_1$ made in the proof of Theorem 3.5, we have
$G_1$ made in the proof of Theorem 3.5, we have ![]() $\dim (\overline {F_1}) \geq \binom {d+1}{2}$. Since
$\dim (\overline {F_1}) \geq \binom {d+1}{2}$. Since ![]() $\dim (\overline {F_2}) \geq 1$, this gives
$\dim (\overline {F_2}) \geq 1$, this gives
 $$ \begin{align*} \binom{d+1}{2} = \dim(\overline{F}) = \dim(\overline{F_1}) + \dim(\overline{F_2})> \binom{d+1}{2}, \end{align*} $$
$$ \begin{align*} \binom{d+1}{2} = \dim(\overline{F}) = \dim(\overline{F_1}) + \dim(\overline{F_2})> \binom{d+1}{2}, \end{align*} $$a contradiction.
3.3 Globally rigid graphs are fully reconstructible
Our goal in this subsection is to prove the following result, which gives an affirmative answer to [Reference Gortler, Theran and Thurston12, Question 7.5].
Theorem 3.6. Let ![]() $d \geq 2$, and let G be a graph on
$d \geq 2$, and let G be a graph on ![]() $n \geq d+2$ vertices that is globally rigid in
$n \geq d+2$ vertices that is globally rigid in ![]() $\mathbb {R}^d$. Then G is fully reconstructible in
$\mathbb {R}^d$. Then G is fully reconstructible in ![]() $\mathbb {C}^d$.
$\mathbb {C}^d$.
Theorem 4.7, below, will lead to examples that show that global rigidity is not necessary for full reconstructibility.
Our proof of Theorem 3.6 uses Theorem 3.5. In fact, as the following theorem shows, the former result is a strengthening of the latter.
Theorem 3.7. Let ![]() $G = (V,E)$ be a graph without isolated vertices, and suppose that G is fully reconstructible in
$G = (V,E)$ be a graph without isolated vertices, and suppose that G is fully reconstructible in ![]() $\mathbb {C}^d$. Then G is
$\mathbb {C}^d$. Then G is ![]() $\mathcal {R}_d$-connected.
$\mathcal {R}_d$-connected.
Proof. Suppose, for a contradiction, that there is a partition ![]() $E = E_1 \cup E_2$ of E into nonempty subsets with
$E = E_1 \cup E_2$ of E into nonempty subsets with ![]() $r_d(E) = r_d(E_1) + r_d(E_2)$, and let
$r_d(E) = r_d(E_1) + r_d(E_2)$, and let ![]() $G_1$ and
$G_1$ and ![]() $G_2$ be the subgraphs induced by
$G_2$ be the subgraphs induced by ![]() $E_1$ and
$E_1$ and ![]() $E_2$, respectively. By Lemma 3.1, this implies
$E_2$, respectively. By Lemma 3.1, this implies ![]() $M_{d,G} = M_{d,G_1} \times M_{d,G_2}$. If
$M_{d,G} = M_{d,G_1} \times M_{d,G_2}$. If ![]() $G_1$ and
$G_1$ and ![]() $G_2$ have at least one vertex in common, then let H be the graph consisting of disjoint copies of
$G_2$ have at least one vertex in common, then let H be the graph consisting of disjoint copies of ![]() $G_1$ and
$G_1$ and ![]() $G_2$. Otherwise, let H be the graph obtained from disjoint copies of
$G_2$. Otherwise, let H be the graph obtained from disjoint copies of ![]() $G_1$ and
$G_1$ and ![]() $G_2$ by identifying some vertex of
$G_2$ by identifying some vertex of ![]() $G_1$ and some vertex of
$G_1$ and some vertex of ![]() $G_2$. In both cases, we have
$G_2$. In both cases, we have ![]() $m_{d,H}(\mathbb {C}^{n'd}) = m_{d,G_1}(\mathbb {C}^{n_1d}) \times m_{d,G_2}(\mathbb {C}^{n_2d})$, where
$m_{d,H}(\mathbb {C}^{n'd}) = m_{d,G_1}(\mathbb {C}^{n_1d}) \times m_{d,G_2}(\mathbb {C}^{n_2d})$, where ![]() $n'$,
$n'$, ![]() $n_1$ and
$n_1$ and ![]() $n_2$ denote the number of vertices of H,
$n_2$ denote the number of vertices of H, ![]() $G_1$ and
$G_1$ and ![]() $G_2$, respectively. It follows that
$G_2$, respectively. It follows that ![]() $M_{d,H} = M_{d,G_1} \times M_{d,G_2}$.Footnote 3 Since by construction G and H are not isomorphic, Theorem 2.19 implies that G is not fully reconstructible, as desired.
$M_{d,H} = M_{d,G_1} \times M_{d,G_2}$.Footnote 3 Since by construction G and H are not isomorphic, Theorem 2.19 implies that G is not fully reconstructible, as desired.
This theorem is similar in spirit to [Reference Garamvölgyi and Jordán8, Theorem 5.21], which states that if G is strongly reconstructible in ![]() $\mathbb {C}^d$ on at least
$\mathbb {C}^d$ on at least ![]() $d+2$ vertices and without isolated vertices, then it cannot contain an
$d+2$ vertices and without isolated vertices, then it cannot contain an ![]() $\mathcal {R}_d$-bridge. Example 4.6 in the next section shows that the converse of Theorem 3.7 is not true: The
$\mathcal {R}_d$-bridge. Example 4.6 in the next section shows that the converse of Theorem 3.7 is not true: The ![]() $6$-ring depicted in Figure 4 is not even strongly reconstructible in
$6$-ring depicted in Figure 4 is not even strongly reconstructible in ![]() $\mathbb {C}^3$, despite being
$\mathbb {C}^3$, despite being ![]() $\mathcal {R}_3$-connected,
$\mathcal {R}_3$-connected, ![]() $4$-connected and redundantly rigid in
$4$-connected and redundantly rigid in ![]() $\mathbb {R}^3$.
$\mathbb {R}^3$.

Figure 2 This graph G is ![]() $4$-connected, redundantly rigid in
$4$-connected, redundantly rigid in ![]() $\mathbb {R}^3$, and
$\mathbb {R}^3$, and ![]() ${\mathcal{R}}_3$-separable. It satisfies
${\mathcal{R}}_3$-separable. It satisfies ![]() $r_3(G)= 105 = 96 + 9 =r_3(G^o)+r_3(K_5)$, where
$r_3(G)= 105 = 96 + 9 =r_3(G^o)+r_3(K_5)$, where ![]() $G^o$ is the outer ring of
$G^o$ is the outer ring of ![]() $K_5$’s.
$K_5$’s.

Figure 3 This graph is also ![]() $4$-connected, redundantly rigid in
$4$-connected, redundantly rigid in ![]() $\mathbb {R}^3$, and
$\mathbb {R}^3$, and ![]() ${\mathcal{R}}_3$-separable.
${\mathcal{R}}_3$-separable.

Figure 4 A graph that is ![]() $4$-connected, redundantly rigid in
$4$-connected, redundantly rigid in ![]() $\mathbb {R}^3$ and
$\mathbb {R}^3$ and ![]() ${\mathcal{R}}_3$-connected but not globally rigid in
${\mathcal{R}}_3$-connected but not globally rigid in ![]() $\mathbb {R}^3$.
$\mathbb {R}^3$.
We now turn our attention to Theorem 3.6. As our argument is quite involved, we start by giving a brief outline of the proof. By Theorem 2.19, to show that the globally rigid graph G is fully reconstructible, we need to show that, whenever ![]() $M_{d,G} =_\psi M_{d,H}$ for some graph H without isolated vertices and some edge bijection
$M_{d,G} =_\psi M_{d,H}$ for some graph H without isolated vertices and some edge bijection ![]() $\psi : E(G) \rightarrow E(H)$, we have that H is isomorphic to G (and the isomorphism induces the appropriate edge bijection). Let n and
$\psi : E(G) \rightarrow E(H)$, we have that H is isomorphic to G (and the isomorphism induces the appropriate edge bijection). Let n and ![]() $n'$ denote the number of vertices of G and H, respectively. If
$n'$ denote the number of vertices of G and H, respectively. If ![]() $n = n'$, then we are done by the strong reconstructibility of G (Theorem 2.20). If
$n = n'$, then we are done by the strong reconstructibility of G (Theorem 2.20). If ![]() $n' < n$, then
$n' < n$, then ![]() $M_{d,H}$ must necessarily be of lower dimension than
$M_{d,H}$ must necessarily be of lower dimension than ![]() $M_{d,G}$, which is impossible. The only remaining possibility to be ruled out is that
$M_{d,G}$, which is impossible. The only remaining possibility to be ruled out is that ![]() $n'>n$; note that in this case
$n'>n$; note that in this case ![]() $M_{d,G} =_\psi M_{d,H}$ (and in particular the equality of dimensions) implies that H is locally flexible in
$M_{d,G} =_\psi M_{d,H}$ (and in particular the equality of dimensions) implies that H is locally flexible in ![]() $\mathbb {R}^d$.
$\mathbb {R}^d$.
We rule this out as follows. From ![]() $M_{d,G} =_\psi M_{d,H}$ and
$M_{d,G} =_\psi M_{d,H}$ and ![]() $M_{d-1,H} \subseteq _\psi M_{d-1,G}$ (which follows from Corollary 3.4), we get bounds on
$M_{d-1,H} \subseteq _\psi M_{d-1,G}$ (which follows from Corollary 3.4), we get bounds on ![]() $k_d$ and
$k_d$ and ![]() $k_{d-1}$, the generic dimension of the space of infinitesimal motions of H in d and
$k_{d-1}$, the generic dimension of the space of infinitesimal motions of H in d and ![]() $d-1$ dimensions, respectively. Using Theorem 3.5, we also get that H is
$d-1$ dimensions, respectively. Using Theorem 3.5, we also get that H is ![]() $\mathcal {R}_d$-connected and in particular connected. The crux of our argument is Corollary 3.12, which states that for a connected graph,
$\mathcal {R}_d$-connected and in particular connected. The crux of our argument is Corollary 3.12, which states that for a connected graph, ![]() $k_d - \binom {d+1}{2}$ (the ‘d-dimensional degrees of freedom’ of the graph) is larger by a multiplicative factor than
$k_d - \binom {d+1}{2}$ (the ‘d-dimensional degrees of freedom’ of the graph) is larger by a multiplicative factor than ![]() $k_{d-1} - \binom {d}{2}$, the
$k_{d-1} - \binom {d}{2}$, the ![]() $(d-1)$-dimensional degrees of freedom of the graph. Applying this to H, we shall get a contradiction with the bounds on
$(d-1)$-dimensional degrees of freedom of the graph. Applying this to H, we shall get a contradiction with the bounds on ![]() $k_d$ and
$k_d$ and ![]() $k_{d-1}$ obtained previously.
$k_{d-1}$ obtained previously.
Before proving Corollary 3.12, we need a number of technical results. The first is about the structure of a certain variety, while the second gives a concrete example of an infinitesimal motion in d dimensions that, generically, cannot be decomposed into two ![]() $(d-1)$-dimensional infinitesimal motions. The subsequent lemmas use this result to obtain bounds on the generic dimension of infinitesimal motions in
$(d-1)$-dimensional infinitesimal motions. The subsequent lemmas use this result to obtain bounds on the generic dimension of infinitesimal motions in ![]() $\mathbb {C}^i$ for all
$\mathbb {C}^i$ for all ![]() $1 \leq i \leq d$.
$1 \leq i \leq d$.
Lemma 3.8. Let ![]() $G = (V,E)$ be a graph on n vertices.
$G = (V,E)$ be a graph on n vertices.
1. The variety
 $M_{1,G} \subseteq \mathbb {C}^E$ is not contained in any (linear) hyperplane in
$M_{1,G} \subseteq \mathbb {C}^E$ is not contained in any (linear) hyperplane in  $\mathbb {C}^E$.
$\mathbb {C}^E$.2. Consider the mapping
 $f : \mathbb {C}^{2n} \rightarrow \mathbb {C}^E$ defined by Then
$f : \mathbb {C}^{2n} \rightarrow \mathbb {C}^E$ defined by Then $$ \begin{align*} p = \left(p_v^{(1)},p_v^{(2)}\right)_{v \in V} \longmapsto \left((p^{(1)}_v - p^{(1)}_u)(p^{(2)}_v - p^{(2)}_u)\right)_{uv \in E}. \end{align*} $$
$$ \begin{align*} p = \left(p_v^{(1)},p_v^{(2)}\right)_{v \in V} \longmapsto \left((p^{(1)}_v - p^{(1)}_u)(p^{(2)}_v - p^{(2)}_u)\right)_{uv \in E}. \end{align*} $$ $\overline {f(\mathbb {C}^{2n})}$ (and consequently
$\overline {f(\mathbb {C}^{2n})}$ (and consequently  $f(\mathbb {C}^{2n})$ itself) is not contained in any (linear) hyperplane in
$f(\mathbb {C}^{2n})$ itself) is not contained in any (linear) hyperplane in  $\mathbb {C}^E$.
$\mathbb {C}^E$.
Proof. a) Let H be an arbitrary hyperplane in ![]() $\mathbb {C}^E$ whose orthogonal complement is generated by some nonzero
$\mathbb {C}^E$ whose orthogonal complement is generated by some nonzero ![]() $\omega \in \mathbb {C}^E$. The configurations
$\omega \in \mathbb {C}^E$. The configurations ![]() $p \in \mathbb {C}^{n}$ for which
$p \in \mathbb {C}^{n}$ for which ![]() $\omega $ is an equilibrium stress of
$\omega $ is an equilibrium stress of ![]() $(G,p)$ form a proper linear subspace of
$(G,p)$ form a proper linear subspace of ![]() $\mathbb {C}^{n}$. In particular, we can find a generic framework
$\mathbb {C}^{n}$. In particular, we can find a generic framework ![]() $(G,p)$ in
$(G,p)$ in ![]() $\mathbb {C}^1$ which does not have
$\mathbb {C}^1$ which does not have ![]() $\omega $ as an equilibrium stress. By Lemma 2.15,
$\omega $ as an equilibrium stress. By Lemma 2.15, ![]() $\omega $ is not in the orthogonal complement of the tangent space of
$\omega $ is not in the orthogonal complement of the tangent space of ![]() $M_{1,G}$ at
$M_{1,G}$ at ![]() $m_{1,G}(p)$. It follows that this tangent space is not contained in H, which implies that
$m_{1,G}(p)$. It follows that this tangent space is not contained in H, which implies that ![]() $M_{1,G}$ is not contained in H either, as desired.
$M_{1,G}$ is not contained in H either, as desired.
b) By direct calculationFootnote 4 we have that ![]() $f = m_{2,G} \circ \alpha $ where
$f = m_{2,G} \circ \alpha $ where ![]() $\alpha : \mathbb {C}^{2n} \rightarrow \mathbb {C}^{2n}$ is defined by
$\alpha : \mathbb {C}^{2n} \rightarrow \mathbb {C}^{2n}$ is defined by
 $$ \begin{align*} p = \left(p^{(1)}_v,p^{(2)}_v\right)_{v \in V} \longmapsto \left(\frac{p^{(1)}_v + p^{(2)}_v}{2}, \frac{p^{(1)}_v - p^{(2)}_v}{2\sqrt{-1}} \right)_{v \in V}. \end{align*} $$
$$ \begin{align*} p = \left(p^{(1)}_v,p^{(2)}_v\right)_{v \in V} \longmapsto \left(\frac{p^{(1)}_v + p^{(2)}_v}{2}, \frac{p^{(1)}_v - p^{(2)}_v}{2\sqrt{-1}} \right)_{v \in V}. \end{align*} $$ Since ![]() $\alpha $ is a linear automorphism of
$\alpha $ is a linear automorphism of ![]() $\mathbb {C}^{2n}$, this implies that
$\mathbb {C}^{2n}$, this implies that ![]() $f(\mathbb {C}^{2n}) = m_{2,G}(\mathbb {C}^{2n})$, and thus
$f(\mathbb {C}^{2n}) = m_{2,G}(\mathbb {C}^{2n})$, and thus ![]() $\overline {f(\mathbb {C}^{2n})} = M_{2,G}$. Now by part a),
$\overline {f(\mathbb {C}^{2n})} = M_{2,G}$. Now by part a), ![]() $M_{1,G}$ is not contained in any linear hyperplane in
$M_{1,G}$ is not contained in any linear hyperplane in ![]() $\mathbb {C}^E$. Since
$\mathbb {C}^E$. Since ![]() $M_{1,G} \subseteq M_{2,G}$, the same holds for
$M_{1,G} \subseteq M_{2,G}$, the same holds for ![]() $M_{2,G}$.
$M_{2,G}$.
For the next two lemmas, we introduce the following notation. Let ![]() $d \geq 3$ and let
$d \geq 3$ and let ![]() $G = (V,E)$ be a graph on n vertices. For a framework
$G = (V,E)$ be a graph on n vertices. For a framework ![]() $(G,p)$ in
$(G,p)$ in ![]() $\mathbb {C}^d$, let
$\mathbb {C}^d$, let ![]() $W_1(G,p) \leq \mathbb {C}^{nd}$ denote the set of infinitesimal motions of
$W_1(G,p) \leq \mathbb {C}^{nd}$ denote the set of infinitesimal motions of ![]() $(G,p)$ that are supported on the first
$(G,p)$ that are supported on the first ![]() $d-1$ coordinates, that is, infinitesimal motions of the form
$d-1$ coordinates, that is, infinitesimal motions of the form ![]() $\left (q_v,0\right )_{v \in V}$, where
$\left (q_v,0\right )_{v \in V}$, where ![]() $q_v \in \mathbb {C}^{d-1}$ for each vertex v. Similarly, let
$q_v \in \mathbb {C}^{d-1}$ for each vertex v. Similarly, let ![]() $W_2(G,p)$ denote the set of infinitesimal motions that are supported on the last
$W_2(G,p)$ denote the set of infinitesimal motions that are supported on the last ![]() $d-1$ coordinates, and let
$d-1$ coordinates, and let ![]() $W(G,p)$ be the subspace of
$W(G,p)$ be the subspace of ![]() $\mathbb {C}^{nd}$ spanned by
$\mathbb {C}^{nd}$ spanned by ![]() $W_1(G,p) \cup W_2(G,p)$.
$W_1(G,p) \cup W_2(G,p)$.
Lemma 3.9. Let ![]() $d \geq 3$ and let
$d \geq 3$ and let ![]() $G = (V,E)$ be a graph on n vertices that is not
$G = (V,E)$ be a graph on n vertices that is not ![]() $\mathcal {R}_{d-2}$-independent. Then for any generic configuration
$\mathcal {R}_{d-2}$-independent. Then for any generic configuration ![]() $p = \left (p_v^{(1)},\dots ,p^{(d)}_v\right )_{v \in V} \in \mathbb {C}^{nd}$, the infinitesimal rotation
$p = \left (p_v^{(1)},\dots ,p^{(d)}_v\right )_{v \in V} \in \mathbb {C}^{nd}$, the infinitesimal rotation ![]() $\varphi = \varphi (p)$ of
$\varphi = \varphi (p)$ of ![]() $(G,p)$ defined by
$(G,p)$ defined by
is not in the subspace ![]() $W(G,p)$. In particular,
$W(G,p)$. In particular, ![]() $W(G,p)$ is a proper subspace of the space of infinitesimal motions of
$W(G,p)$ is a proper subspace of the space of infinitesimal motions of ![]() $(G,p)$.
$(G,p)$.
Proof. Consider an arbitrary realization ![]() $(G,p)$ in
$(G,p)$ in ![]() $\mathbb {C}^d$, and let
$\mathbb {C}^d$, and let ![]() $\widetilde {p} \in \mathbb {C}^{n(d-2)}$ denote the projection of p onto the middle
$\widetilde {p} \in \mathbb {C}^{n(d-2)}$ denote the projection of p onto the middle ![]() $d-2$ coordinate axes. Suppose that
$d-2$ coordinate axes. Suppose that ![]() $\varphi (p)$ can be written as
$\varphi (p)$ can be written as ![]() $\varphi (p) = q + r$, where
$\varphi (p) = q + r$, where ![]() $q \in W_1(G,p)$ and
$q \in W_1(G,p)$ and ![]() $r \in W_2(G,p)$. Then
$r \in W_2(G,p)$. Then ![]() $q_v = (- p_v^{(d)}, \widetilde {q}_v, 0)$ for every vertex
$q_v = (- p_v^{(d)}, \widetilde {q}_v, 0)$ for every vertex ![]() $v \in V$, where
$v \in V$, where ![]() $\widetilde {q} = (\widetilde {q}_v)_{v \in V} \in \mathbb {C}^{n(d-2)}$. Since q is an infinitesimal motion, we have that
$\widetilde {q} = (\widetilde {q}_v)_{v \in V} \in \mathbb {C}^{n(d-2)}$. Since q is an infinitesimal motion, we have that
Using the above description of q and rearranging gives
We shall show that, for a generic realization ![]() $(G,p)$ of G in
$(G,p)$ of G in ![]() $\mathbb {C}^d$, equation (3.2) cannot hold for any vector
$\mathbb {C}^d$, equation (3.2) cannot hold for any vector ![]() $\left (\widetilde {q}_v\right )_{v \in V}$. We start by observing that
$\left (\widetilde {q}_v\right )_{v \in V}$. We start by observing that ![]() $(G,\widetilde {p})$ is a generic framework in
$(G,\widetilde {p})$ is a generic framework in ![]() $\mathbb {C}^{d-2}$, so
$\mathbb {C}^{d-2}$, so ![]() $\operatorname {\mathrm {rank}}(R(G,\widetilde {p}))$ is equal to the rank
$\operatorname {\mathrm {rank}}(R(G,\widetilde {p}))$ is equal to the rank ![]() $r = r_{d-2}(G)$ of G, which is the maximal rank of the rigidity matrix of any framework in
$r = r_{d-2}(G)$ of G, which is the maximal rank of the rigidity matrix of any framework in ![]() $\mathbb {C}^{d-2}$. Note that
$\mathbb {C}^{d-2}$. Note that
so it is sufficient to show that the vector ![]() $z = \left ((p_v^{(1)} - p_u^{(1)})(p_v^{(d)} - p_u^{(d)}\right )_{uv \in E}$ is not contained in
$z = \left ((p_v^{(1)} - p_u^{(1)})(p_v^{(d)} - p_u^{(d)}\right )_{uv \in E}$ is not contained in ![]() $\operatorname {\mathrm {span}}(R(G,\widetilde {p}))$. This is the same as saying
$\operatorname {\mathrm {span}}(R(G,\widetilde {p}))$. This is the same as saying ![]() $\operatorname {\mathrm {rk}}(M(p)) = r + 1$, where
$\operatorname {\mathrm {rk}}(M(p)) = r + 1$, where ![]() $M(p)$ is obtained by appending the column vector z to
$M(p)$ is obtained by appending the column vector z to ![]() $R(G,\widetilde {p})$, which is further equivalent to the nonvanishing of some
$R(G,\widetilde {p})$, which is further equivalent to the nonvanishing of some ![]() $(r+1) \times (r+1)$ subdeterminant of
$(r+1) \times (r+1)$ subdeterminant of ![]() $M(p)$. The entries of
$M(p)$. The entries of ![]() $M(p)$ are polynomial functions in the coordinates of
$M(p)$ are polynomial functions in the coordinates of ![]() $(G,p)$ with rational coefficients and consequently so are these
$(G,p)$ with rational coefficients and consequently so are these ![]() $(r+1) \times (r+1)$ subdeterminants.
$(r+1) \times (r+1)$ subdeterminants.
Since ![]() $(G,p)$ is generic, it is sufficient to show that at least one of the polynomial functions describing these subdeterminants is not identically zero; in other words, that there is some framework
$(G,p)$ is generic, it is sufficient to show that at least one of the polynomial functions describing these subdeterminants is not identically zero; in other words, that there is some framework ![]() $(G,p')$ for which the corresponding matrix
$(G,p')$ for which the corresponding matrix ![]() $M(p')$ has rank
$M(p')$ has rank ![]() $r+1$. In fact, we can find such a framework by only modifying the first and last coordinates of
$r+1$. In fact, we can find such a framework by only modifying the first and last coordinates of ![]() $p_v$ for each
$p_v$ for each ![]() $v \in V$. Since G is not
$v \in V$. Since G is not ![]() $\mathcal {R}_{d-2}$-independent,
$\mathcal {R}_{d-2}$-independent, ![]() $r < |E|$, and thus,
$r < |E|$, and thus, ![]() $\operatorname {\mathrm {span}}(R(G,\widetilde {p}))$ is contained in some linear hyperplane
$\operatorname {\mathrm {span}}(R(G,\widetilde {p}))$ is contained in some linear hyperplane ![]() $H \subseteq \mathbb {C}^E$. By part b) of Lemma 3.8, we can find some vectors
$H \subseteq \mathbb {C}^E$. By part b) of Lemma 3.8, we can find some vectors ![]() $(x_v)_{v \in V}$ and
$(x_v)_{v \in V}$ and ![]() $(y_v)_{v \in V}$ such that the vector
$(y_v)_{v \in V}$ such that the vector ![]() $\left ((x_v - x_u)(y_v-y_u)\right )_{uv \in E}$ is not contained in H. It follows that the framework
$\left ((x_v - x_u)(y_v-y_u)\right )_{uv \in E}$ is not contained in H. It follows that the framework ![]() $(G,p')$ defined by
$(G,p')$ defined by ![]() $p^{\prime }_v = (x_v,\widetilde {p}_v,q_v), v \in V$ satisfies
$p^{\prime }_v = (x_v,\widetilde {p}_v,q_v), v \in V$ satisfies ![]() $\operatorname {\mathrm {rk}}(M(p')) = r+1$, as desired.
$\operatorname {\mathrm {rk}}(M(p')) = r+1$, as desired.
Lemma 3.10. Let ![]() $d \geq 3$, and let G be a graph on n vertices that is not
$d \geq 3$, and let G be a graph on n vertices that is not ![]() $\mathcal {R}_{d-2}$-independent. For
$\mathcal {R}_{d-2}$-independent. For ![]() $i = 1,\ldots ,d$, let
$i = 1,\ldots ,d$, let ![]() $k_i$ denote the dimension of the space of infinitesimal motions of a generic realization of G in
$k_i$ denote the dimension of the space of infinitesimal motions of a generic realization of G in ![]() $\mathbb {C}^i$. Then for
$\mathbb {C}^i$. Then for ![]() $i = 1,\ldots ,d-2$, we have
$i = 1,\ldots ,d-2$, we have
Proof. The assumption that G is not ![]() $\mathcal {R}_{d-2}$-independent implies that it is not
$\mathcal {R}_{d-2}$-independent implies that it is not ![]() $\mathcal {R}_i$-independent for all
$\mathcal {R}_i$-independent for all ![]() $1 \leq i \leq d-2$. Thus, it is sufficient to prove for
$1 \leq i \leq d-2$. Thus, it is sufficient to prove for ![]() $i = d-2$. By Lemma 3.9, there is a generic realization
$i = d-2$. By Lemma 3.9, there is a generic realization ![]() $(G,p)$ in
$(G,p)$ in ![]() $\mathbb {C}^d$ such that
$\mathbb {C}^d$ such that ![]() $W(G,p)$ is a proper subset of the space of infinitesimal motions of
$W(G,p)$ is a proper subset of the space of infinitesimal motions of ![]() $(G,p)$. Note that
$(G,p)$. Note that ![]() $\dim (W_1(G,p)) = \dim (W_2(G,p)) = k_{d-1}$, and by the choice of
$\dim (W_1(G,p)) = \dim (W_2(G,p)) = k_{d-1}$, and by the choice of ![]() $(G,p)$, we have
$(G,p)$, we have ![]() $\dim (W(G,p)) \leq k_d - 1$. Moreover, the subspace
$\dim (W(G,p)) \leq k_d - 1$. Moreover, the subspace ![]() $W' = W_1(G,p) \cap W_2(G,p)$ consists of the infinitesimal motions of
$W' = W_1(G,p) \cap W_2(G,p)$ consists of the infinitesimal motions of ![]() $(G,p)$ that are supported on the middle
$(G,p)$ that are supported on the middle ![]() $d-2$ coordinates. This implies
$d-2$ coordinates. This implies ![]() $\dim (W') = k_{d-2}$. By basic linear algebra we have
$\dim (W') = k_{d-2}$. By basic linear algebra we have
Substituting the above equalities and inequality and then rearranging gives
as desired.
If G is ![]() $\mathcal {R}_{d-2}$-independent, then the conclusion of Lemma 3.10 does not hold. In this case, G is
$\mathcal {R}_{d-2}$-independent, then the conclusion of Lemma 3.10 does not hold. In this case, G is ![]() $\mathcal {R}_{d-1}$-independent and
$\mathcal {R}_{d-1}$-independent and ![]() $\mathcal {R}_d$-independent as well, so we have
$\mathcal {R}_d$-independent as well, so we have ![]() $k_i = ni - |E|$ for
$k_i = ni - |E|$ for ![]() $d - 2 \leq i \leq d$ so that
$d - 2 \leq i \leq d$ so that ![]() $k_{d} - k_{d-1} = k_{d-1} - k_{d-2}$.
$k_{d} - k_{d-1} = k_{d-1} - k_{d-2}$.
The following combinatorial lemma lets us turn the recursive bound on ![]() $k_i$ given in Lemma 3.10 into a lower bound that only depends on
$k_i$ given in Lemma 3.10 into a lower bound that only depends on ![]() $k_d$ and
$k_d$ and ![]() $k_{d-1}$.
$k_{d-1}$.
Lemma 3.11. Let ![]() $d \geq 2$ be an integer, and let
$d \geq 2$ be an integer, and let ![]() $k_1,k_2,\ldots ,k_d \in \mathbb {Z}$ be a sequence of integers with
$k_1,k_2,\ldots ,k_d \in \mathbb {Z}$ be a sequence of integers with ![]() $k_d = \binom {d+1}{2} + x$ and
$k_d = \binom {d+1}{2} + x$ and ![]() $k_{d-1} = \binom {d}{2} + y$ for some
$k_{d-1} = \binom {d}{2} + y$ for some ![]() $x,y \in \mathbb {Z}$. Suppose that for
$x,y \in \mathbb {Z}$. Suppose that for ![]() $1 \leq i \leq d-2$ we have
$1 \leq i \leq d-2$ we have ![]() $k_{i+2} - k_{i+1} \geq k_{i+1} - k_{i} + 1$. Then for
$k_{i+2} - k_{i+1} \geq k_{i+1} - k_{i} + 1$. Then for ![]() $1 \leq i \leq d-1$ we have
$1 \leq i \leq d-1$ we have ![]() $k_i \geq \binom {i+1}{2} + (d-i)(y-x) + x$.
$k_i \geq \binom {i+1}{2} + (d-i)(y-x) + x$.
Proof. Consider the numbers ![]() $l_i = k_i - \binom {i+1}{2}$ for
$l_i = k_i - \binom {i+1}{2}$ for ![]() $i = 1,\ldots ,d$. Our goal is to prove
$i = 1,\ldots ,d$. Our goal is to prove ![]() $l_i \geq (d-i)(y-x) + x$. By definition, we have
$l_i \geq (d-i)(y-x) + x$. By definition, we have ![]() $l_{d-1} - l_{d} = y - x$. We claim that
$l_{d-1} - l_{d} = y - x$. We claim that ![]() $l_i - l_{i+1} \geq l_{i+1} - l_{i+2}$ holds for all
$l_i - l_{i+1} \geq l_{i+1} - l_{i+2}$ holds for all ![]() $i = 1, \ldots , d-2$. Indeed, using the bound on
$i = 1, \ldots , d-2$. Indeed, using the bound on ![]() $k_i$ we obtain
$k_i$ we obtain
 $$ \begin{align*} l_i = k_i - \binom{i+1}{2} &\geq 2k_{i+1} - k_{i+2} + 1 - \binom{i+1}{2} \\ &= (2 \binom{i+2}{2} - \binom{i+3}{2} - \binom{i+1}{2} + 1) + (2l_{i+1} - l_{i+2}) \\ &=2l_{i+1} - l_{i+2}, \end{align*} $$
$$ \begin{align*} l_i = k_i - \binom{i+1}{2} &\geq 2k_{i+1} - k_{i+2} + 1 - \binom{i+1}{2} \\ &= (2 \binom{i+2}{2} - \binom{i+3}{2} - \binom{i+1}{2} + 1) + (2l_{i+1} - l_{i+2}) \\ &=2l_{i+1} - l_{i+2}, \end{align*} $$where we used the fact that for all ![]() $a \geq 1$,
$a \geq 1$, ![]() $\binom {a}{2} + \binom {a+2}{2} = 2\binom {a+1}{2} + 1$. This also gives
$\binom {a}{2} + \binom {a+2}{2} = 2\binom {a+1}{2} + 1$. This also gives
The statement now follows easily by induction on ![]() $j = d-i$. For
$j = d-i$. For ![]() $j=1$, we need
$j=1$, we need ![]() $l_{d-1} \geq y$, which is actually satisfied with equality. Now let us assume
$l_{d-1} \geq y$, which is actually satisfied with equality. Now let us assume ![]() $1 < j < d$. Then by induction we have
$1 < j < d$. Then by induction we have
as desired.
If G is a connected graph, then its one-dimensional generic realizations have a one-dimensional space of infinitesimal motions. For such graphs, combining Lemma 3.10 with the bound on ![]() $k_1$ given by Lemma 3.11 gives the following corollary.
$k_1$ given by Lemma 3.11 gives the following corollary.
Corollary 3.12. Let ![]() $d \geq 3$ be an integer and G a connected graph, and suppose that G is not
$d \geq 3$ be an integer and G a connected graph, and suppose that G is not ![]() $\mathcal {R}_{d-2}$-independent. Let
$\mathcal {R}_{d-2}$-independent. Let ![]() $k_{d-1}$ and
$k_{d-1}$ and ![]() $k_d$ denote the dimension of the space of infinitesimal motions of a generic realization of G in
$k_d$ denote the dimension of the space of infinitesimal motions of a generic realization of G in ![]() $\mathbb {C}^{d-1}$ and in
$\mathbb {C}^{d-1}$ and in ![]() $\mathbb {C}^d$, respectively. Finally, let
$\mathbb {C}^d$, respectively. Finally, let ![]() $\operatorname {\mathrm {dof}}_{d-1}(G) = k_{d-1} - \binom {d}{2}$ and
$\operatorname {\mathrm {dof}}_{d-1}(G) = k_{d-1} - \binom {d}{2}$ and ![]() $\operatorname {\mathrm {dof}}_{d}(G) = k_d - \binom {d+1}{2}$ denote the ‘degrees of freedom’ of G in
$\operatorname {\mathrm {dof}}_{d}(G) = k_d - \binom {d+1}{2}$ denote the ‘degrees of freedom’ of G in ![]() $d-1$ and d dimensions, respectively. Then we have
$d-1$ and d dimensions, respectively. Then we have
Now we are ready to prove our main theorem.
Proof of Theorem 3.6.
The ![]() $d=2$ case follows from Theorem 2.21, so we only prove for
$d=2$ case follows from Theorem 2.21, so we only prove for ![]() $d \geq 3$. Let H be a graph on
$d \geq 3$. Let H be a graph on ![]() $n'$ vertices, without isolated vertices and such that
$n'$ vertices, without isolated vertices and such that ![]() $M_{d,G} =_\psi M_{d,H}$ under some edge bijection
$M_{d,G} =_\psi M_{d,H}$ under some edge bijection ![]() $\psi $. Then by Corollary 3.4, we also have
$\psi $. Then by Corollary 3.4, we also have ![]() $M_{d-1,H} \subseteq _\psi M_{d-1,G}$. Observe that, since G is globally rigid, it is
$M_{d-1,H} \subseteq _\psi M_{d-1,G}$. Observe that, since G is globally rigid, it is ![]() $\mathcal {R}_d$-connected by Theorem 3.5, and thus, so is H by Theorem 2.14 and the equality of the measurement varieties. In particular, H is a connected graph, and it is not
$\mathcal {R}_d$-connected by Theorem 3.5, and thus, so is H by Theorem 2.14 and the equality of the measurement varieties. In particular, H is a connected graph, and it is not ![]() $\mathcal {R}_d$-independent and thus not
$\mathcal {R}_d$-independent and thus not ![]() $\mathcal {R}_{d-2}$-independent.
$\mathcal {R}_{d-2}$-independent.
Let ![]() $s = n'-n$, and let
$s = n'-n$, and let ![]() $k_i$ denote the dimension of the space of infinitesimal motions of a generic realization of H in
$k_i$ denote the dimension of the space of infinitesimal motions of a generic realization of H in ![]() $\mathbb {C}^i$ for
$\mathbb {C}^i$ for ![]() $1 = 1,\ldots ,d$. By considering the dimension of
$1 = 1,\ldots ,d$. By considering the dimension of ![]() $M_{d,G}$ (using Lemma 2.13) and using the assumption that G is (globally) rigid, we get
$M_{d,G}$ (using Lemma 2.13) and using the assumption that G is (globally) rigid, we get ![]() $n'd - k_d = nd - \binom {d+1}{2}$, implying
$n'd - k_d = nd - \binom {d+1}{2}$, implying ![]() $k_d = sd + \binom {d+1}{2}$. Similarly, from
$k_d = sd + \binom {d+1}{2}$. Similarly, from ![]() $M_{d-1,H} \subseteq _\psi M_{d-1,G}$, we have
$M_{d-1,H} \subseteq _\psi M_{d-1,G}$, we have ![]() $n'(d-1) - k_{d-1} \leq n(d-1) - \binom {d}{2},$ so that
$n'(d-1) - k_{d-1} \leq n(d-1) - \binom {d}{2},$ so that ![]() $k_{d-1} \geq s(d-1) + \binom {d}{2}$. Note that here we used the fact that if G is (globally) rigid in
$k_{d-1} \geq s(d-1) + \binom {d}{2}$. Note that here we used the fact that if G is (globally) rigid in ![]() $\mathbb {R}^d$, then it is rigid in
$\mathbb {R}^d$, then it is rigid in ![]() $\mathbb {R}^{d-1}$; see, e.g., [Reference Jordán, Whiteley, Goodman, O’Rourke and Tóth16, Theorem 63.2.11].
$\mathbb {R}^{d-1}$; see, e.g., [Reference Jordán, Whiteley, Goodman, O’Rourke and Tóth16, Theorem 63.2.11].
Since ![]() $k_d \geq \binom {d+1}{2}$, we must have
$k_d \geq \binom {d+1}{2}$, we must have ![]() $s \geq 0$. On the other hand, since H is connected and not
$s \geq 0$. On the other hand, since H is connected and not ![]() $\mathcal {R}_{d-2}$-independent, Corollary 3.12 implies that
$\mathcal {R}_{d-2}$-independent, Corollary 3.12 implies that
Reordering, we get
which is equivalent to ![]() $s \leq 0$. It follows that
$s \leq 0$. It follows that ![]() $s = 0$, so G and H have the same number of vertices. By Theorem 2.20, G is strongly reconstructible in
$s = 0$, so G and H have the same number of vertices. By Theorem 2.20, G is strongly reconstructible in ![]() $\mathbb {C}^d$, so
$\mathbb {C}^d$, so ![]() $\psi $ is induced by a graph isomorphism
$\psi $ is induced by a graph isomorphism ![]() $\varphi : G \rightarrow H$, as desired.
$\varphi : G \rightarrow H$, as desired.
Applying Theorem 3.6 to a globally rigid subgraph of a graph, we obtain the following corollary.
Corollary 3.13. Let ![]() $d \geq 2$, and let
$d \geq 2$, and let ![]() $(G,p)$ and
$(G,p)$ and ![]() $(H,q)$ be generic frameworks in
$(H,q)$ be generic frameworks in ![]() $\mathbb {C}^d$ that are length-equivalent under the edge bijection
$\mathbb {C}^d$ that are length-equivalent under the edge bijection ![]() $\psi $. Let
$\psi $. Let ![]() $G_0 = (V_0,E_0)$ be a globally rigid subgraph of
$G_0 = (V_0,E_0)$ be a globally rigid subgraph of ![]() $G = (V,E)$, and let
$G = (V,E)$, and let ![]() $H_0$ denote the subgraph of H induced by
$H_0$ denote the subgraph of H induced by ![]() $\psi (E_0)$. Then
$\psi (E_0)$. Then ![]() $\left .\psi \right |{}_{E_0}$ is induced by an isomorphism
$\left .\psi \right |{}_{E_0}$ is induced by an isomorphism ![]() $\varphi : V(G_0) \rightarrow V(H_0)$, and the frameworks
$\varphi : V(G_0) \rightarrow V(H_0)$, and the frameworks ![]() $(G_0,\left .p\right |{}_{V_0})$ and
$(G_0,\left .p\right |{}_{V_0})$ and ![]() $(H_0,\left .q\right |{}_{V(H_0)} \circ \varphi )$ are congruent.
$(H_0,\left .q\right |{}_{V(H_0)} \circ \varphi )$ are congruent.
The ![]() $d = 2$ case of Corollary 3.13 can be found in [Reference Garamvölgyi and Jordán8, Corollary 5.2].
$d = 2$ case of Corollary 3.13 can be found in [Reference Garamvölgyi and Jordán8, Corollary 5.2].
To close this section, let us briefly return to Lemma 3.10. Let G be a graph and, as before, let ![]() $k_d$ denote the dimension of the set of infinitesimal motions of a generic realization of G in
$k_d$ denote the dimension of the set of infinitesimal motions of a generic realization of G in ![]() $\mathbb {C}^d$. Using the fact that, for a graph G on at least
$\mathbb {C}^d$. Using the fact that, for a graph G on at least ![]() $d+2$ vertices we have
$d+2$ vertices we have ![]() $r_d(G) = nd - k_d$, we can rephrase the
$r_d(G) = nd - k_d$, we can rephrase the ![]() $i = d-2$ case of Lemma 3.10 in the following way.
$i = d-2$ case of Lemma 3.10 in the following way.
Corollary 3.14. Let ![]() $d \geq 3$, and let G be a graph that is not
$d \geq 3$, and let G be a graph that is not ![]() $\mathcal {R}_{d-2}$-independent. Then the rank of G satisfies
$\mathcal {R}_{d-2}$-independent. Then the rank of G satisfies
This bound is the best possible in the sense that if G is rigid in ![]() $\mathbb {R}^{d}$, then equation (3.3) is satisfied with equality. We note that Corollary 3.14 can be interpreted as a statement about the so-called secant defect of
$\mathbb {R}^{d}$, then equation (3.3) is satisfied with equality. We note that Corollary 3.14 can be interpreted as a statement about the so-called secant defect of ![]() $M_{1,G}$, similar to Zak’s theorem on superadditivity [Reference Fantechi7, Reference Zak25]; see [Reference Gortler, Healy and Thurston10, Section 4.3] for a related discussion.
$M_{1,G}$, similar to Zak’s theorem on superadditivity [Reference Fantechi7, Reference Zak25]; see [Reference Gortler, Healy and Thurston10, Section 4.3] for a related discussion.
4 Examples and open questions
In this section, we examine various examples related to ![]() $\mathcal {R}_d$-connected and
$\mathcal {R}_d$-connected and ![]() $\mathcal {R}_d$-separable graphs, as well as the unlabeled reconstruction problem.
$\mathcal {R}_d$-separable graphs, as well as the unlabeled reconstruction problem.
4.1 New examples of H-graphs
Following [Reference Jordán, Király and Tanigawa15], we say that a graph G is an H-graph in ![]() $\mathbb {R}^d$ if it is
$\mathbb {R}^d$ if it is ![]() $(d+1)$-connected and redundantly rigid in
$(d+1)$-connected and redundantly rigid in ![]() $\mathbb {R}^d$ (i.e., it satisfies the necessary conditions of Theorem 2.1), but it is not globally rigid in
$\mathbb {R}^d$ (i.e., it satisfies the necessary conditions of Theorem 2.1), but it is not globally rigid in ![]() $\mathbb {R}^d$. There are no H-graphs for
$\mathbb {R}^d$. There are no H-graphs for ![]() $d=1,2$, but for
$d=1,2$, but for ![]() $d\geq 3$ they exist, and finding more examples may lead to a better understanding of higher-dimensional global rigidity. For a long time, the complete bipartite graph
$d\geq 3$ they exist, and finding more examples may lead to a better understanding of higher-dimensional global rigidity. For a long time, the complete bipartite graph ![]() $K_{5,5}$ was the only known H-graph in
$K_{5,5}$ was the only known H-graph in ![]() $\mathbb {R}^3$ (identified in [Reference Connelly4]), until infinite families had been found in [Reference Jordán, Király and Tanigawa15].
$\mathbb {R}^3$ (identified in [Reference Connelly4]), until infinite families had been found in [Reference Jordán, Király and Tanigawa15].
Theorem 3.5 can be used to give new examples of H-graphs which are ![]() $\mathcal {R}_3$-separable. These also demonstrate that redundant rigidity and
$\mathcal {R}_3$-separable. These also demonstrate that redundant rigidity and ![]() $(d+1)$-connectivity together do not imply
$(d+1)$-connectivity together do not imply ![]() $\mathcal {R}_d$-connectivity in the
$\mathcal {R}_d$-connectivity in the ![]() $d \geq 3$ case.
$d \geq 3$ case.
Example 4.1. Consider the construction illustrated in Figure 2. It is easy to see that the graph G in the figure is ![]() $4$-connected.
$4$-connected.
Claim. G is redundantly rigid and ![]() $\mathcal {R}_3$-separable.
$\mathcal {R}_3$-separable.
Proof. We show that G is rigid by showing that a spanning subgraph of G can be reduced to ![]() $K_4$ by a sequence of the following operations: (i) deletion of a vertex of degree at least three, (ii) deletion of a vertex v of degree four and the addition of a new edge between two neighbours of v, (iii) the contraction of an edge
$K_4$ by a sequence of the following operations: (i) deletion of a vertex of degree at least three, (ii) deletion of a vertex v of degree four and the addition of a new edge between two neighbours of v, (iii) the contraction of an edge ![]() $uv$ for which u and v have exactly two common neighbours. It is well-known that the inverse operations (
$uv$ for which u and v have exactly two common neighbours. It is well-known that the inverse operations (![]() $0$- and
$0$- and ![]() $1$-extension and vertex splitting) preserve rigidity in
$1$-extension and vertex splitting) preserve rigidity in ![]() $\mathbb {R}^3$, see e.g. [Reference Whiteley23]. Thus, since
$\mathbb {R}^3$, see e.g. [Reference Whiteley23]. Thus, since ![]() $K_4$ is rigid, it will follow that G is also rigid.
$K_4$ is rigid, it will follow that G is also rigid.
First, delete the nine vertices of degree four from G, and then delete one edge from each of the remaining copies of ![]() $K_5$. The resulting graph has
$K_5$. The resulting graph has ![]() $28$ vertices and
$28$ vertices and ![]() $78$ edges. We shall reduce it to its internal
$78$ edges. We shall reduce it to its internal ![]() $K_4$ subgraph. By the symmetry of the graph, we can perform the reduction steps in groups of four in a symmetric way. First, we contract four edges of the outer ring that do not belong to the four copies of
$K_4$ subgraph. By the symmetry of the graph, we can perform the reduction steps in groups of four in a symmetric way. First, we contract four edges of the outer ring that do not belong to the four copies of ![]() $K_5-e$, one from each ‘corner’. These operations create a vertex of degree four in each corner, so we can apply operation (ii) at each of them to obtain a graph on
$K_5-e$, one from each ‘corner’. These operations create a vertex of degree four in each corner, so we can apply operation (ii) at each of them to obtain a graph on ![]() $20$ vertices and
$20$ vertices and ![]() $54$ edges, in which the four edges added form a four-cycle. After that we again apply operation (ii) in three rounds, decreasing the number of vertices by four in each round. If the added edges are chosen appropriately, we obtain a graph on
$54$ edges, in which the four edges added form a four-cycle. After that we again apply operation (ii) in three rounds, decreasing the number of vertices by four in each round. If the added edges are chosen appropriately, we obtain a graph on ![]() $8$ vertices, consisting of the internal
$8$ vertices, consisting of the internal ![]() $K_4$, a disjoint four-cycle
$K_4$, a disjoint four-cycle ![]() $C_4$, and eight more edges that connect them (so that they span an
$C_4$, and eight more edges that connect them (so that they span an ![]() $8$-cycle). From here we apply operations (ii), (i), (ii) and then again (i) to get the
$8$-cycle). From here we apply operations (ii), (i), (ii) and then again (i) to get the ![]() $K_4$ subgraph.
$K_4$ subgraph.
Thus, G is indeed rigid, that is, ![]() $r_3(G)=3|V(G)|-6=105$. Note that G is also redundantly rigid, because every edge of G belongs to a
$r_3(G)=3|V(G)|-6=105$. Note that G is also redundantly rigid, because every edge of G belongs to a ![]() $K_5$ subgraph. To see that G is
$K_5$ subgraph. To see that G is ![]() $\mathcal {R}_3$-separable, first observe that if we remove one edge from each copy of
$\mathcal {R}_3$-separable, first observe that if we remove one edge from each copy of ![]() $K_5$ in the outer ring
$K_5$ in the outer ring ![]() $G^o$ (say, one edge incident with each vertex of degree four), then we do not decrease its rank and obtain a spanning subgraph of
$G^o$ (say, one edge incident with each vertex of degree four), then we do not decrease its rank and obtain a spanning subgraph of ![]() $G^o$ with
$G^o$ with ![]() $96$ edges. Thus,
$96$ edges. Thus, ![]() $r_3(G^o)\leq 96$. The inner
$r_3(G^o)\leq 96$. The inner ![]() $K_5$ has rank
$K_5$ has rank ![]() $9$. Hence, we must have
$9$. Hence, we must have ![]() $r_3(G)=r_3(G^o)+r_3(K_5)$, showing that G is indeed
$r_3(G)=r_3(G^o)+r_3(K_5)$, showing that G is indeed ![]() $\mathcal {R}_3$-separable.
$\mathcal {R}_3$-separable.
Since ![]() $\mathcal {R}_3$-separable graphs are not globally rigid in
$\mathcal {R}_3$-separable graphs are not globally rigid in ![]() $\mathbb {R}^3$ by Theorem 3.5, G is indeed an H-graph in
$\mathbb {R}^3$ by Theorem 3.5, G is indeed an H-graph in ![]() $\mathbb {R}^3$. We can obtain an infinite family of H-graphs in
$\mathbb {R}^3$. We can obtain an infinite family of H-graphs in ![]() $\mathbb {R}^3$ from Example 4.1 by replacing the inner
$\mathbb {R}^3$ from Example 4.1 by replacing the inner ![]() $K_5$ in Figure 2 with another
$K_5$ in Figure 2 with another ![]() $4$-connected redundantly rigid graph
$4$-connected redundantly rigid graph ![]() $K'$ in
$K'$ in ![]() $\mathbb {R}^3$ on at least five vertices (as in Figure 3, where
$\mathbb {R}^3$ on at least five vertices (as in Figure 3, where ![]() $K'=K_6-e$).
$K'=K_6-e$).
We note that some of the H-graphs obtained in [Reference Jordán, Király and Tanigawa15] (for example, the ‘![]() $6$-ring’ depicted in Figure 4) show that
$6$-ring’ depicted in Figure 4) show that ![]() $4$-connectivity, redundant rigidity and
$4$-connectivity, redundant rigidity and ![]() $\mathcal {R}_3$-connectivity together do not imply global rigidity in
$\mathcal {R}_3$-connectivity together do not imply global rigidity in ![]() $\mathbb {R}^3$.
$\mathbb {R}^3$.
It is also interesting to note that every known H-graph in ![]() $\mathbb {R}^3$, except
$\mathbb {R}^3$, except ![]() $K_{5,5}$, has a
$K_{5,5}$, has a ![]() $4$-separator.
$4$-separator.
Question 4.2. Is every ![]() $5$-connected and redundantly rigid graph, other than
$5$-connected and redundantly rigid graph, other than ![]() $K_{5,5}$, globally rigid in
$K_{5,5}$, globally rigid in ![]() $\mathbb {R}^3$?
$\mathbb {R}^3$?
The following related question also seems to be open.
Question 4.3. Is every ![]() $5$-connected and redundantly rigid graph
$5$-connected and redundantly rigid graph ![]() $\mathcal {R}_3$-connected?
$\mathcal {R}_3$-connected?
It is easy to see that coning increases vertex connectivity by one so that the cone of a ![]() $(d+1)$-connected graph is
$(d+1)$-connected graph is ![]() $(d+2)$-connected. It is also folklore (and follows from Theorem 2.4(a) and Lemma 5.3 in the next section) that if G is redundantly rigid in
$(d+2)$-connected. It is also folklore (and follows from Theorem 2.4(a) and Lemma 5.3 in the next section) that if G is redundantly rigid in ![]() $\mathbb {R}^d$, then its cone graph
$\mathbb {R}^d$, then its cone graph ![]() $G^v$ is redundantly rigid in
$G^v$ is redundantly rigid in ![]() $\mathbb {R}^{d+1}$. Together with Theorem 2.4(b) these imply that the cone of a H-graph in
$\mathbb {R}^{d+1}$. Together with Theorem 2.4(b) these imply that the cone of a H-graph in ![]() $\mathbb {R}^d$ is a H-graph in
$\mathbb {R}^d$ is a H-graph in ![]() $\mathbb {R}^{d+1}$. We can use this fact to construct further families of H-graphs. However, these graphs will not be
$\mathbb {R}^{d+1}$. We can use this fact to construct further families of H-graphs. However, these graphs will not be ![]() $\mathcal {R}_{d+1}$-separable (see Theorem 5.4). Instead, we can use higher-dimensional body-hinge graphs [Reference Jordán, Király and Tanigawa15] to generalize the
$\mathcal {R}_{d+1}$-separable (see Theorem 5.4). Instead, we can use higher-dimensional body-hinge graphs [Reference Jordán, Király and Tanigawa15] to generalize the ![]() $\mathcal {R}_{3}$-separable construction of Figure 2 to
$\mathcal {R}_{3}$-separable construction of Figure 2 to ![]() $d\geq 4$. We omit the details.
$d\geq 4$. We omit the details.
4.2 Unlabeled reconstructibility and small separators
In [Reference Gortler, Theran and Thurston12, Question 7.2], the authors asked whether every graph G that is ![]() $3$-connected and redundantly rigid in
$3$-connected and redundantly rigid in ![]() $\mathbb {R}^d$ is determined by its measurement variety, that is, whether
$\mathbb {R}^d$ is determined by its measurement variety, that is, whether ![]() $M_{d,G} =_\psi M_{d,H}$ under some edge bijection
$M_{d,G} =_\psi M_{d,H}$ under some edge bijection ![]() $\psi $ implies that G and H are isomorphic (note that here we do not require that the isomorphism induces
$\psi $ implies that G and H are isomorphic (note that here we do not require that the isomorphism induces ![]() $\psi $). Such a graph was called ‘weakly reconstructible in
$\psi $). Such a graph was called ‘weakly reconstructible in ![]() $\mathbb {C}^d$’ in [Reference Garamvölgyi and Jordán8]. In the other direction, in [Reference Garamvölgyi and Jordán8, Section 7], the authors asked whether every graph on at least
$\mathbb {C}^d$’ in [Reference Garamvölgyi and Jordán8]. In the other direction, in [Reference Garamvölgyi and Jordán8, Section 7], the authors asked whether every graph on at least ![]() $d+2$ vertices that is strongly reconstructible in
$d+2$ vertices that is strongly reconstructible in ![]() $\mathbb {C}^d$ for some
$\mathbb {C}^d$ for some ![]() $d \geq 3$ is globally rigid in
$d \geq 3$ is globally rigid in ![]() $\mathbb {R}^d$ or (more weakly) whether it is
$\mathbb {R}^d$ or (more weakly) whether it is ![]() $(d+1)$-connected.
$(d+1)$-connected.
In this subsection, we provide negative answers to each of these questions for ![]() $d\geq 3$. Throughout this section, we shall use the following (folklore) result which also appears in the proof of [Reference Garamvölgyi and Jordán8, Theorem 5.21].
$d\geq 3$. Throughout this section, we shall use the following (folklore) result which also appears in the proof of [Reference Garamvölgyi and Jordán8, Theorem 5.21].
Lemma 4.4. Let G and H be graphs on at least three vertices with G connected, and let ![]() $\varphi _1, \varphi _2: V(G) \rightarrow V(H)$ be injective graph homomorphisms. Suppose that
$\varphi _1, \varphi _2: V(G) \rightarrow V(H)$ be injective graph homomorphisms. Suppose that ![]() $\varphi _1$ and
$\varphi _1$ and ![]() $\varphi _2$ induce the same edge map
$\varphi _2$ induce the same edge map ![]() $\psi : E(G) \rightarrow E(H)$. Then
$\psi : E(G) \rightarrow E(H)$. Then ![]() $\varphi _1(v) = \varphi _2(v)$ for all
$\varphi _1(v) = \varphi _2(v)$ for all ![]() $v \in V(G)$.
$v \in V(G)$.
Proof. Let ![]() $v \in V(G)$ be a vertex of degree at least two, and let
$v \in V(G)$ be a vertex of degree at least two, and let ![]() $vu,vu' \in E(G)$ be a pair of edges incident to v. Now
$vu,vu' \in E(G)$ be a pair of edges incident to v. Now ![]() $\varphi _1(v)$ is the unique vertex in H that is an end-vertex of both
$\varphi _1(v)$ is the unique vertex in H that is an end-vertex of both ![]() $\psi (vu)$ and
$\psi (vu)$ and ![]() $\psi (vu')$. Since
$\psi (vu')$. Since ![]() $\varphi _2(v)$ can be described in the same way, we have
$\varphi _2(v)$ can be described in the same way, we have ![]() $\varphi _1(v) = \varphi _2(v)$. Note that in a connected graph on at least three vertices, every edge has at least one end-vertex with degree at least two. This shows that
$\varphi _1(v) = \varphi _2(v)$. Note that in a connected graph on at least three vertices, every edge has at least one end-vertex with degree at least two. This shows that ![]() $\varphi _1$ and
$\varphi _1$ and ![]() $\varphi _2$ send at least one vertex of each edge in G to the same vertex in H. Since they also send each edge in G to the same edge in H, they must agree on every vertex of G.
$\varphi _2$ send at least one vertex of each edge in G to the same vertex in H. Since they also send each edge in G to the same edge in H, they must agree on every vertex of G.
Example 4.5. Consider again the graph G shown in Figure 2. As we have seen in Example 4.1, G is ![]() $4$-connected, redundantly rigid and
$4$-connected, redundantly rigid and ![]() $\mathcal {R}_3$-separable.
$\mathcal {R}_3$-separable.
Claim. G is not strongly reconstructible in ![]() $\mathbb {C}^3$.
$\mathbb {C}^3$.
Proof. By the ![]() $\mathcal {R}_3$-separability of G and Lemma 3.1, we have
$\mathcal {R}_3$-separability of G and Lemma 3.1, we have ![]() $M_{d,G} = M_{d,G^o} \times M_{d,K_5}$, where
$M_{d,G} = M_{d,G^o} \times M_{d,K_5}$, where ![]() $K_5$ denotes the complete subgraph of G induced by the inner five vertices. Let
$K_5$ denotes the complete subgraph of G induced by the inner five vertices. Let ![]() $\psi $ be a permutation of the edges of G that leaves the edges of
$\psi $ be a permutation of the edges of G that leaves the edges of ![]() $G^o$ in place and permutes the edges of
$G^o$ in place and permutes the edges of ![]() $K_5$ according to some permutation of its five vertices. Then
$K_5$ according to some permutation of its five vertices. Then ![]() $M_{d,G} =_\psi M_{d,G}$, i.e.,
$M_{d,G} =_\psi M_{d,G}$, i.e., ![]() $M_{d,G}$ is invariant under the permutation of the coordinate axes in
$M_{d,G}$ is invariant under the permutation of the coordinate axes in ![]() $\mathbb {C}^{E(G)}$ induced by
$\mathbb {C}^{E(G)}$ induced by ![]() $\psi $. However,
$\psi $. However, ![]() $\psi $ is not induced by a graph automorphism of G: Since it leaves the edges of
$\psi $ is not induced by a graph automorphism of G: Since it leaves the edges of ![]() $G^o$ in place, by Lemma 4.4, such an automorphism would have to leave the vertices of
$G^o$ in place, by Lemma 4.4, such an automorphism would have to leave the vertices of ![]() $G^o$ in place and thus be the identity map on G, which does not induce
$G^o$ in place and thus be the identity map on G, which does not induce ![]() $\psi $. By Theorem 2.19, this shows that G is not strongly reconstructible.
$\psi $. By Theorem 2.19, this shows that G is not strongly reconstructible.
It can be shown similarly that the graph ![]() $G'$ shown in Figure 3 is not even weakly reconstructible in
$G'$ shown in Figure 3 is not even weakly reconstructible in ![]() $\mathbb {C}^3$: The graph obtained by adding the missing edge to the inner
$\mathbb {C}^3$: The graph obtained by adding the missing edge to the inner ![]() $K_6$ and removing a different edge from it has the same measurement variety as
$K_6$ and removing a different edge from it has the same measurement variety as ![]() $G'$, even though the two graphs are not isomorphic. These examples can also be generalized to higher dimensions using the results on body-hinge graphs in [Reference Jordán, Király and Tanigawa15].
$G'$, even though the two graphs are not isomorphic. These examples can also be generalized to higher dimensions using the results on body-hinge graphs in [Reference Jordán, Király and Tanigawa15].
The graphs considered in Example 4.5 are all ![]() $\mathcal {R}_3$-separable. The next example is of an
$\mathcal {R}_3$-separable. The next example is of an ![]() $\mathcal {R}_3$-connected graph that is not strongly reconstructible in
$\mathcal {R}_3$-connected graph that is not strongly reconstructible in ![]() $\mathbb {C}^3$.
$\mathbb {C}^3$.
Example 4.6. Let G be the ![]() $6$-ring of
$6$-ring of ![]() $K_5$’s shown in Figure 4. As noted before, it is
$K_5$’s shown in Figure 4. As noted before, it is ![]() $4$-connected, redundantly rigid in
$4$-connected, redundantly rigid in ![]() $\mathbb {R}^3$ and
$\mathbb {R}^3$ and ![]() $\mathcal {R}_3$-connected.
$\mathcal {R}_3$-connected.
Claim. G is not strongly reconstructible in ![]() $\mathbb {C}^3$.
$\mathbb {C}^3$.
Proof. Let v be a vertex of degree four, and let us denote the vertices of the ![]() $K_5$ subgraph that contains v by
$K_5$ subgraph that contains v by ![]() $\{v,a,b,c,d\}$, where the edges
$\{v,a,b,c,d\}$, where the edges ![]() $ab$ and
$ab$ and ![]() $cd$ are shared by neighbouring
$cd$ are shared by neighbouring ![]() $K_5$’s. Let
$K_5$’s. Let ![]() $H = G - v$. It is easy to check that the edges
$H = G - v$. It is easy to check that the edges ![]() $ac,ad,bc,bd$ are all
$ac,ad,bc,bd$ are all ![]() $\mathcal {R}_3$-bridges in H. Thus, by Lemma 3.1, we have
$\mathcal {R}_3$-bridges in H. Thus, by Lemma 3.1, we have ![]() $M_{d,H}=M_{d,H'}\oplus \mathbb {C}^4$, where
$M_{d,H}=M_{d,H'}\oplus \mathbb {C}^4$, where ![]() $H'=H-\{ac,ad,bc,bd\}$. Let
$H'=H-\{ac,ad,bc,bd\}$. Let ![]() $(G,p)$ be a generic realization of G, and (by a slight abuse of notation) let
$(G,p)$ be a generic realization of G, and (by a slight abuse of notation) let ![]() $(H,p)$ be its restriction to H.
$(H,p)$ be its restriction to H.
Consider the permutation ![]() $\psi $ of the edges of H that leaves the edges of
$\psi $ of the edges of H that leaves the edges of ![]() $H'$ in place and maps
$H'$ in place and maps ![]() $ac,ad,bc,bd$ to
$ac,ad,bc,bd$ to ![]() $bd,bc,ad,ac$, respectively. Since
$bd,bc,ad,ac$, respectively. Since ![]() $M_{d,H}$ is invariant under the permutation of coordinate axes induced by
$M_{d,H}$ is invariant under the permutation of coordinate axes induced by ![]() $\psi $, Lemma 2.12 implies that there exists a generic realization
$\psi $, Lemma 2.12 implies that there exists a generic realization ![]() $(H,q)$ of H in
$(H,q)$ of H in ![]() $\mathbb {C}^3$ such that
$\mathbb {C}^3$ such that ![]() $(H',q|_{V(H')})$ and
$(H',q|_{V(H')})$ and ![]() $(H',p|_{V(H')})$ are equivalent and
$(H',p|_{V(H')})$ are equivalent and ![]() $m_{ac}(p)=m_{bd}(q)$,
$m_{ac}(p)=m_{bd}(q)$, ![]() $m_{bd}(p)=m_{ac}(q)$,
$m_{bd}(p)=m_{ac}(q)$, ![]() $m_{bc}(p)=m_{ad}(q)$, and
$m_{bc}(p)=m_{ad}(q)$, and ![]() $m_{ad}(p)=m_{bc}(q)$. This implies that the point configurations
$m_{ad}(p)=m_{bc}(q)$. This implies that the point configurations ![]() $(p(a),p(b),p(c),p(d))$ and
$(p(a),p(b),p(c),p(d))$ and ![]() $(q(b),q(a),q(d),q(c))$ are congruent, i.e., the points in them have the same pairwise squared distances. Since by genericity they have full affine span, this also implies that they are strongly congruent, in other words, there is a rigid motion of
$(q(b),q(a),q(d),q(c))$ are congruent, i.e., the points in them have the same pairwise squared distances. Since by genericity they have full affine span, this also implies that they are strongly congruent, in other words, there is a rigid motion of ![]() $\mathbb {C}^3$ that maps
$\mathbb {C}^3$ that maps ![]() $p(a), p(b), p(c), p(d)$ to
$p(a), p(b), p(c), p(d)$ to ![]() $q(b),q(a),q(d),q(c)$, respectively.
$q(b),q(a),q(d),q(c)$, respectively.
Let us extend ![]() $(H,q)$ to a realization
$(H,q)$ to a realization ![]() $(G,q)$ by defining
$(G,q)$ by defining ![]() $q(v)$ to be the image of
$q(v)$ to be the image of ![]() $p(v)$ under this rigid motion, and let us also extend
$p(v)$ under this rigid motion, and let us also extend ![]() $\psi $ to all of
$\psi $ to all of ![]() $E(G)$ by mapping
$E(G)$ by mapping ![]() $va,vb,vc,vd$ to
$va,vb,vc,vd$ to ![]() $vb,va,vd,vc$, respectively. Then
$vb,va,vd,vc$, respectively. Then ![]() $m_{d,G}(p) = m_{d,G}(q)$ under the edge permutation
$m_{d,G}(p) = m_{d,G}(q)$ under the edge permutation ![]() $\psi $. On the other hand,
$\psi $. On the other hand, ![]() $\psi $ is not induced by a graph automorphism of G: Since it leaves the edges of
$\psi $ is not induced by a graph automorphism of G: Since it leaves the edges of ![]() $H'$ in place, by Lemma 4.4 such an automorphism would leave the vertices of
$H'$ in place, by Lemma 4.4 such an automorphism would leave the vertices of ![]() $H'$ in place, and consequently, it would have to be the identity map on G, which does not induce
$H'$ in place, and consequently, it would have to be the identity map on G, which does not induce ![]() $\psi $. By Theorem 2.19, this shows that G is not strongly reconstructible in
$\psi $. By Theorem 2.19, this shows that G is not strongly reconstructible in ![]() $\mathbb {C}^3$, as desired.
$\mathbb {C}^3$, as desired.
Finally, we construct examples of fully reconstructible graphs with small separators. In the next proof, we shall use the following fact. Let ![]() $G_1, G_2$ be rigid graphs in
$G_1, G_2$ be rigid graphs in ![]() $\mathbb {R}^d$ on at least
$\mathbb {R}^d$ on at least ![]() $d+1$ vertices, and let G be obtained from
$d+1$ vertices, and let G be obtained from ![]() $G_1$ and
$G_1$ and ![]() $G_2$ by identifying k pairs of vertices. Then if
$G_2$ by identifying k pairs of vertices. Then if ![]() $0 \leq k \leq d - 1$, we have
$0 \leq k \leq d - 1$, we have ![]() $r_d(G) = d|V(G)| - \binom {d+1}{2} - \binom {d-k+1}{2}$, and if
$r_d(G) = d|V(G)| - \binom {d+1}{2} - \binom {d-k+1}{2}$, and if ![]() $k \geq d$, then G is rigid. This follows, e.g., from the ‘gluing lemma’ [Reference Whiteley23, Lemma 11.1.9], or it can be seen directly by considering the infinitesimal motions of a generic realization of G in
$k \geq d$, then G is rigid. This follows, e.g., from the ‘gluing lemma’ [Reference Whiteley23, Lemma 11.1.9], or it can be seen directly by considering the infinitesimal motions of a generic realization of G in ![]() $\mathbb {R}^d$.
$\mathbb {R}^d$.
Theorem 4.7. Let ![]() $G = (V,E)$ be a graph with induced subgraphs
$G = (V,E)$ be a graph with induced subgraphs ![]() $G_1 = (V_1,E_1)$ and
$G_1 = (V_1,E_1)$ and ![]() $G_2 = (V_2,E_2)$ for which
$G_2 = (V_2,E_2)$ for which ![]() $V_1 \cup V_2 = V$ and
$V_1 \cup V_2 = V$ and ![]() $V_1 \cap V_2$ induces a connected subgraph of G on at least three vertices. Let
$V_1 \cap V_2$ induces a connected subgraph of G on at least three vertices. Let ![]() $d \geq 1$. If
$d \geq 1$. If ![]() $G_1$ and
$G_1$ and ![]() $G_2$ are fully reconstructible rigid graphs on at least
$G_2$ are fully reconstructible rigid graphs on at least ![]() $d+1$ vertices in
$d+1$ vertices in ![]() $\mathbb {C}^d$, then G is fully reconstructible in
$\mathbb {C}^d$, then G is fully reconstructible in ![]() $\mathbb {C}^d$.
$\mathbb {C}^d$.
Proof. By Theorem 2.19, it suffices to show that if for some graph H we have ![]() $M_{d,G} =_\psi M_{d,H}$ under some edge bijection
$M_{d,G} =_\psi M_{d,H}$ under some edge bijection ![]() $\psi $, then
$\psi $, then ![]() $\psi $ is induced by a graph isomorphism
$\psi $ is induced by a graph isomorphism ![]() $\varphi : V(G) \rightarrow V(H)$. Let
$\varphi : V(G) \rightarrow V(H)$. Let ![]() $H_1, H_2$ be the subgraphs of H induced by
$H_1, H_2$ be the subgraphs of H induced by ![]() $\psi (E_1)$ and
$\psi (E_1)$ and ![]() $\psi (E_2)$, respectively. Now for
$\psi (E_2)$, respectively. Now for ![]() $i=1,2$,
$i=1,2$, ![]() $M_{d,G_i} = M_{d,H_i}$, so by the full reconstructibility of
$M_{d,G_i} = M_{d,H_i}$, so by the full reconstructibility of ![]() $G_i$, there is a graph isomorphism
$G_i$, there is a graph isomorphism ![]() $\varphi _i : V_i \rightarrow V(H_i)$ that induces
$\varphi _i : V_i \rightarrow V(H_i)$ that induces ![]() $\left .\psi \right |{}_{E_i}$. Since
$\left .\psi \right |{}_{E_i}$. Since ![]() $V_1 \cap V_2$ induces a connected subgraph of G, Lemma 4.4 applies to
$V_1 \cap V_2$ induces a connected subgraph of G, Lemma 4.4 applies to ![]() $\varphi _1|_{V_1 \cap V_2}$ and
$\varphi _1|_{V_1 \cap V_2}$ and ![]() $\varphi _2|_{V_1 \cap V_2}$, giving
$\varphi _2|_{V_1 \cap V_2}$, giving ![]() $\varphi _1(v) = \varphi _2(v)$ for all
$\varphi _1(v) = \varphi _2(v)$ for all ![]() $v \in V_1 \cap V_2$.
$v \in V_1 \cap V_2$.
It follows that H is the union of two subgraphs ![]() $H_1,H_2$ which are isomorphic to
$H_1,H_2$ which are isomorphic to ![]() $G_1,G_2$, respectively, and have
$G_1,G_2$, respectively, and have ![]() $k\geq |V_1\cap V_2|$ vertices in common. Let
$k\geq |V_1\cap V_2|$ vertices in common. Let ![]() $\ell = |V_1\cap V_2|\geq 3$. We first show that
$\ell = |V_1\cap V_2|\geq 3$. We first show that ![]() $k = \ell $. Note that
$k = \ell $. Note that ![]() $|V(G)|=|V_1|+|V_2|- \ell $ and
$|V(G)|=|V_1|+|V_2|- \ell $ and ![]() $|V(H)|=|V_1|+|V_2|- k$, and hence
$|V(H)|=|V_1|+|V_2|- k$, and hence ![]() $|V(H)|-|V(G)|=l-k$.
$|V(H)|-|V(G)|=l-k$.
Let us first consider the ![]() $k\leq d-1$ case. Since by Theorem 2.14 the d-dimensional rigidity matroids of G and H are isomorphic, we obtain
$k\leq d-1$ case. Since by Theorem 2.14 the d-dimensional rigidity matroids of G and H are isomorphic, we obtain
 $$ \begin{align*} d|V(G)| -\binom{d+1}{2}-\binom{d-\ell +1}{2} = r_d(G) = r_d(H) = d|V(H)|-\binom{d+1}{2}-\binom{d-k+1}{2}. \end{align*} $$
$$ \begin{align*} d|V(G)| -\binom{d+1}{2}-\binom{d-\ell +1}{2} = r_d(G) = r_d(H) = d|V(H)|-\binom{d+1}{2}-\binom{d-k+1}{2}. \end{align*} $$This gives
 $$ \begin{align*} \binom{d+1}{2} + \binom{k}{2} = dk + \binom{d-k+1}{2} = d\ell + \binom{d-\ell+1}{2} = \binom{d+1}{2} + \binom{\ell}{2}, \end{align*} $$
$$ \begin{align*} \binom{d+1}{2} + \binom{k}{2} = dk + \binom{d-k+1}{2} = d\ell + \binom{d-\ell+1}{2} = \binom{d+1}{2} + \binom{\ell}{2}, \end{align*} $$where the second equality comes from the previous equation and the first and third equalities from direct calculation. It follows that ![]() $k=\ell $. An analogous argument shows that
$k=\ell $. An analogous argument shows that ![]() $k = \ell $ holds in the
$k = \ell $ holds in the ![]() $k\geq d$ case as well.
$k\geq d$ case as well.
This implies that the only vertices of H that are in the image of both ![]() $\varphi _1$ and
$\varphi _1$ and ![]() $\varphi _2$ are those in the image of
$\varphi _2$ are those in the image of ![]() $V_1 \cap V_2$, where
$V_1 \cap V_2$, where ![]() $\varphi _1$ and
$\varphi _1$ and ![]() $\varphi _2$ agree. Hence, we can ‘glue’
$\varphi _2$ agree. Hence, we can ‘glue’ ![]() $\varphi _1$ and
$\varphi _1$ and ![]() $\varphi _2$, i.e. the mapping
$\varphi _2$, i.e. the mapping ![]() $\varphi : V \rightarrow V(H)$ defined by
$\varphi : V \rightarrow V(H)$ defined by ![]() $\varphi |_{V_i} = \varphi _i, i = 1,2$ is well-defined and is an isomorphism (in particular, it is injective). Then
$\varphi |_{V_i} = \varphi _i, i = 1,2$ is well-defined and is an isomorphism (in particular, it is injective). Then ![]() $\varphi $ induces
$\varphi $ induces ![]() $\psi $, as required.
$\psi $, as required.
In fact, the proof shows that we can slightly relax the conditions in Theorem 4.7 by only requiring that each connected component of the graph induced by ![]() $V_1 \cap V_2$ has at least three vertices.
$V_1 \cap V_2$ has at least three vertices.
Example 4.8. Let ![]() $d \geq 1$, and let
$d \geq 1$, and let ![]() $G_d$ be the graph obtained by gluing two copies of the complete graph
$G_d$ be the graph obtained by gluing two copies of the complete graph ![]() $K_{d+2}$ along three pairs of vertices. Theorems 3.6 and 4.7 imply that
$K_{d+2}$ along three pairs of vertices. Theorems 3.6 and 4.7 imply that ![]() $G_d$ is fully reconstructible in
$G_d$ is fully reconstructible in ![]() $\mathbb {C}^d$. This example shows that fully (or strongly) reconstructible graphs need not be
$\mathbb {C}^d$. This example shows that fully (or strongly) reconstructible graphs need not be ![]() $(d+1)$-connected in the
$(d+1)$-connected in the ![]() $d \geq 3$ case, which gives a negative answer to a question posed in [Reference Garamvölgyi and Jordán8, Section 7]. Also note that for
$d \geq 3$ case, which gives a negative answer to a question posed in [Reference Garamvölgyi and Jordán8, Section 7]. Also note that for ![]() $d \geq 4$,
$d \geq 4$, ![]() $G_d$ is not even rigid in
$G_d$ is not even rigid in ![]() $\mathbb {R}^d$. It is unclear whether there exist nonrigid fully reconstructible graphs in
$\mathbb {R}^d$. It is unclear whether there exist nonrigid fully reconstructible graphs in ![]() $\mathbb {C}^3$.
$\mathbb {C}^3$.
The previous example also shows that a fully reconstructible graph in ![]() $\mathbb {C}^d$ need not be globally rigid in
$\mathbb {C}^d$ need not be globally rigid in ![]() $\mathbb {R}^d$ in the
$\mathbb {R}^d$ in the ![]() $d \geq 3$ case. Another such example is given in [Reference Bernstein and Gortler2], where it is shown, using a computer-assisted proof, that the complete bipartite graph
$d \geq 3$ case. Another such example is given in [Reference Bernstein and Gortler2], where it is shown, using a computer-assisted proof, that the complete bipartite graph ![]() $K_{5,5}$ is fully reconstructible in
$K_{5,5}$ is fully reconstructible in ![]() $\mathbb {C}^3$. A combinatorial characterization of fully reconstructible graphs in
$\mathbb {C}^3$. A combinatorial characterization of fully reconstructible graphs in ![]() $\mathbb {C}^d$ seems elusive, even in the
$\mathbb {C}^d$ seems elusive, even in the ![]() $d = 3$ case.
$d = 3$ case.
4.3 Monotonicity of unlabeled reconstructibility
The graph ![]() $G_d$ of Example 4.8 also shows that for
$G_d$ of Example 4.8 also shows that for ![]() $d \geq 4$, edge addition does not necessarily preserve strong (or full) reconstructibility in
$d \geq 4$, edge addition does not necessarily preserve strong (or full) reconstructibility in ![]() $\mathbb {C}^d$. Indeed,
$\mathbb {C}^d$. Indeed, ![]() $G_d$ is fully reconstructible in
$G_d$ is fully reconstructible in ![]() $\mathbb {C}^d$, but for any pair of nonneighbouring vertices
$\mathbb {C}^d$, but for any pair of nonneighbouring vertices ![]() $u,v \in V(G_d)$,
$u,v \in V(G_d)$, ![]() $uv$ is an
$uv$ is an ![]() $\mathcal {R}_d$-bridge in
$\mathcal {R}_d$-bridge in ![]() $G_d + uv$. [Reference Garamvölgyi and Jordán8, Theorem 5.21] states that strongly reconstructible graphs in
$G_d + uv$. [Reference Garamvölgyi and Jordán8, Theorem 5.21] states that strongly reconstructible graphs in ![]() $\mathbb {C}^d$ (on at least
$\mathbb {C}^d$ (on at least ![]() $d+2$ vertices and without isolated vertices) do not contain
$d+2$ vertices and without isolated vertices) do not contain ![]() $\mathcal {R}_d$-bridges so that
$\mathcal {R}_d$-bridges so that ![]() $G_d + uv$ is not strongly reconstructible in
$G_d + uv$ is not strongly reconstructible in ![]() $\mathbb {C}^d$. It would be interesting to see whether this phenomenon can only happen if the newly added edge is an
$\mathbb {C}^d$. It would be interesting to see whether this phenomenon can only happen if the newly added edge is an ![]() $\mathcal {R}_d$-bridge.
$\mathcal {R}_d$-bridge.
Question 4.9. Let ![]() $d \geq 1$, and let
$d \geq 1$, and let ![]() $G = (V,E)$ be a graph on at least
$G = (V,E)$ be a graph on at least ![]() $d+2$ vertices that is strongly reconstructible in
$d+2$ vertices that is strongly reconstructible in ![]() $\mathbb {C}^d$ (fully reconstructible in
$\mathbb {C}^d$ (fully reconstructible in ![]() $\mathbb {C}^d$, respectively). Is it true that if for some pair of vertices
$\mathbb {C}^d$, respectively). Is it true that if for some pair of vertices ![]() $u,v \in V$ we have
$u,v \in V$ we have ![]() $uv \notin E$ and
$uv \notin E$ and ![]() $r_d(G) = r_d(G + uv)$, then
$r_d(G) = r_d(G + uv)$, then ![]() $G + uv$ is strongly reconstructible in
$G + uv$ is strongly reconstructible in ![]() $\mathbb {C}^d$ (fully reconstructible in
$\mathbb {C}^d$ (fully reconstructible in ![]() $\mathbb {C}^d$, respectively)?
$\mathbb {C}^d$, respectively)?
We can prove the following weaker result. We say that a pair ![]() $\{u,v\}$ of vertices in a graph G is globally linked in G in
$\{u,v\}$ of vertices in a graph G is globally linked in G in ![]() $\mathbb {C}^d$ if for every generic framework
$\mathbb {C}^d$ if for every generic framework ![]() $(G,p)$ in
$(G,p)$ in ![]() $\mathbb {C}^d$ and every equivalent realization
$\mathbb {C}^d$ and every equivalent realization ![]() $(G,q)$, we have
$(G,q)$, we have ![]() $m_{uv}(p) = m_{uv}(q)$.
$m_{uv}(p) = m_{uv}(q)$.
Lemma 4.10. Let ![]() $G = (V,E)$ be a strongly reconstructible graph in
$G = (V,E)$ be a strongly reconstructible graph in ![]() $\mathbb {C}^d$, and suppose that a pair of vertices
$\mathbb {C}^d$, and suppose that a pair of vertices ![]() $u,v \in V$ is globally linked in G in
$u,v \in V$ is globally linked in G in ![]() $\mathbb {C}^d$. Then
$\mathbb {C}^d$. Then ![]() $G' = G + uv$ is strongly reconstructible in
$G' = G + uv$ is strongly reconstructible in ![]() $\mathbb {C}^d$. Moreover, if G is fully reconstructible in
$\mathbb {C}^d$. Moreover, if G is fully reconstructible in ![]() $\mathbb {C}^d$, then so is
$\mathbb {C}^d$, then so is ![]() $G'$.
$G'$.
Proof. By Theorem 2.19, it is sufficient to show that if ![]() $M_{d,G'} =_\psi M_{d,H'}$ under some edge bijection
$M_{d,G'} =_\psi M_{d,H'}$ under some edge bijection ![]() $\psi $, where
$\psi $, where ![]() $H'$ is a graph on the same number of vertices as
$H'$ is a graph on the same number of vertices as ![]() $G'$, then
$G'$, then ![]() $\psi $ is induced by a graph isomorphism. Let H denote
$\psi $ is induced by a graph isomorphism. Let H denote ![]() $H' - \psi (uv)$. Then
$H' - \psi (uv)$. Then ![]() $M_{d,G} =_\psi M_{d,H}$ under the edge bijection
$M_{d,G} =_\psi M_{d,H}$ under the edge bijection ![]() $\psi |_{E(G)}$, and thus again by Theorem 2.19, the strong reconstructibility of G implies that
$\psi |_{E(G)}$, and thus again by Theorem 2.19, the strong reconstructibility of G implies that ![]() $\psi |_{E(G)}$ is induced by a graph isomorphism
$\psi |_{E(G)}$ is induced by a graph isomorphism ![]() $\varphi : V(G) \rightarrow V(H)$. It is sufficient to show that
$\varphi : V(G) \rightarrow V(H)$. It is sufficient to show that ![]() $\psi (uv) = \varphi (u)\varphi (v)$. After composing
$\psi (uv) = \varphi (u)\varphi (v)$. After composing ![]() $\psi $ with the edge bijection induced by
$\psi $ with the edge bijection induced by ![]() $\varphi ^{-1}$, this amounts to showing that if
$\varphi ^{-1}$, this amounts to showing that if ![]() $M_{d,G + uv} =_{\psi '} M_{d,G + u'v'}$ under the edge bijection
$M_{d,G + uv} =_{\psi '} M_{d,G + u'v'}$ under the edge bijection ![]() $\psi '$ that fixes the edges of G and sends
$\psi '$ that fixes the edges of G and sends ![]() $uv$ to
$uv$ to ![]() $u'v'$, then
$u'v'$, then ![]() $\{u',v'\} = \{u,v\}$.
$\{u',v'\} = \{u,v\}$.
Let ![]() $(G,p)$ be a generic realization of G in
$(G,p)$ be a generic realization of G in ![]() $\mathbb {C}^d$. By Lemma 2.12, there is a generic realization
$\mathbb {C}^d$. By Lemma 2.12, there is a generic realization ![]() $(G,q)$, equivalent to
$(G,q)$, equivalent to ![]() $(G,p)$ and such that
$(G,p)$ and such that ![]() $m_{uv}(p) = m_{u'v'}(q)$. Since
$m_{uv}(p) = m_{u'v'}(q)$. Since ![]() $\{u,v\}$ is globally linked in G, we must also have
$\{u,v\}$ is globally linked in G, we must also have ![]() $m_{uv}(p) = m_{uv}(q)$. It follows from the genericity of q that
$m_{uv}(p) = m_{uv}(q)$. It follows from the genericity of q that ![]() $\{u,v\} = \{u',v'\}$, as required.
$\{u,v\} = \{u',v'\}$, as required.
The same proof works when G is fully reconstructible in ![]() $\mathbb {C}^d$.
$\mathbb {C}^d$.
We may also consider the effect of edge deletion on unlabeled reconstructibility. The analogue of Question 4.9 for deleting edges is not true: It is not difficult to find an example of a graph G that is strongly (or fully) reconstructible in ![]() $\mathbb {C}^d$ but for which
$\mathbb {C}^d$ but for which ![]() $G - uv$ is not strongly (or fully) reconstructible for some edge
$G - uv$ is not strongly (or fully) reconstructible for some edge ![]() $uv \in E$, even though
$uv \in E$, even though ![]() $r_d(G - uv) = r_d(G)$. This can happen, e.g., if G is globally rigid and
$r_d(G - uv) = r_d(G)$. This can happen, e.g., if G is globally rigid and ![]() $G - uv$ contains an
$G - uv$ contains an ![]() $\mathcal {R}_d$-bridge. However, it is possible that the analogue of Lemma 4.10 for edge deletions is true.
$\mathcal {R}_d$-bridge. However, it is possible that the analogue of Lemma 4.10 for edge deletions is true.
Question 4.11. Let ![]() $d \geq 3$, and let
$d \geq 3$, and let ![]() $G = (V,E)$ be strongly reconstructible in
$G = (V,E)$ be strongly reconstructible in ![]() $\mathbb {C}^d$ (fully reconstructible in
$\mathbb {C}^d$ (fully reconstructible in ![]() $\mathbb {C}^d$, respectively). Is it true that if for some edge
$\mathbb {C}^d$, respectively). Is it true that if for some edge ![]() $uv \in E$ we have that
$uv \in E$ we have that ![]() $\{u,v\}$ is globally linked in
$\{u,v\}$ is globally linked in ![]() $G-uv$, then
$G-uv$, then ![]() $G-uv$ is strongly reconstructible in
$G-uv$ is strongly reconstructible in ![]() $\mathbb {C}^d$ (fully reconstructible in
$\mathbb {C}^d$ (fully reconstructible in ![]() $\mathbb {C}^d$, respectively)?
$\mathbb {C}^d$, respectively)?
The characterization of strong and full reconstructibility in ![]() $\mathbb {C}^1$ and
$\mathbb {C}^1$ and ![]() $\mathbb {C}^2$ given by Theorem 2.21 shows that, for
$\mathbb {C}^2$ given by Theorem 2.21 shows that, for ![]() $d = 2$, the answer to Question 4.11 is positive, while for
$d = 2$, the answer to Question 4.11 is positive, while for ![]() $d=1$, it is negative: Let G be a
$d=1$, it is negative: Let G be a ![]() $3$-connected graph, and suppose that
$3$-connected graph, and suppose that ![]() $G - uv$ is not
$G - uv$ is not ![]() $3$-connected for some edge
$3$-connected for some edge ![]() $uv \in E(G)$. Then G is fully reconstructible in
$uv \in E(G)$. Then G is fully reconstructible in ![]() $\mathbb {C}^1$ and
$\mathbb {C}^1$ and ![]() $\{u,v\}$ is globally linked in
$\{u,v\}$ is globally linked in ![]() $G-uv$ (in fact,
$G-uv$ (in fact, ![]() $G-uv$ is globally rigid in
$G-uv$ is globally rigid in ![]() $\mathbb {R}^1$), but
$\mathbb {R}^1$), but ![]() $G - uv$ is not strongly reconstructible in
$G - uv$ is not strongly reconstructible in ![]() $\mathbb {C}^d$.
$\mathbb {C}^d$.
5 Graphs with nonseparable rigidity matroids
In light of Theorem 3.5, the combinatorial properties of ![]() $\mathcal {R}_d$-connected graphs may be of interest in studying global rigidity. However, not much seems to be known about these graphs in the
$\mathcal {R}_d$-connected graphs may be of interest in studying global rigidity. However, not much seems to be known about these graphs in the ![]() $d \geq 3$ case. In this section, we collect three results related to this notion.
$d \geq 3$ case. In this section, we collect three results related to this notion.
Theorem 5.1. Let ![]() $G=(V,E)$ be an
$G=(V,E)$ be an ![]() $\mathcal {R}_d$-connected graph. Then G is
$\mathcal {R}_d$-connected graph. Then G is ![]() $\mathcal {R}_{d'}$-connected for all
$\mathcal {R}_{d'}$-connected for all ![]() $1\leq d'\leq d$.
$1\leq d'\leq d$.
Proof. It suffices to consider the ![]() $d\geq 2$ case and show that G is
$d\geq 2$ case and show that G is ![]() $\mathcal {R}_{d-1}$-connected. We may also assume that G is an
$\mathcal {R}_{d-1}$-connected. We may also assume that G is an ![]() $\mathcal {R}_d$-circuit. Consider a generic realization
$\mathcal {R}_d$-circuit. Consider a generic realization ![]() $(G,p)$ of G in
$(G,p)$ of G in ![]() $\mathbb {R}^d$. Since G is an
$\mathbb {R}^d$. Since G is an ![]() $\mathcal {R}_d$-circuit, there exists a unique, (up to scalar multiplication) nonzero equilibrium stress
$\mathcal {R}_d$-circuit, there exists a unique, (up to scalar multiplication) nonzero equilibrium stress ![]() $\omega = (\omega _e)_{e \in E}$ of
$\omega = (\omega _e)_{e \in E}$ of ![]() $(G,p)$, which is nonzero on every edge
$(G,p)$, which is nonzero on every edge ![]() $e\in E$.
$e\in E$.
For a contradiction, suppose that G is ![]() $\mathcal {R}_{d-1}$-separable, and let
$\mathcal {R}_{d-1}$-separable, and let ![]() $E_1,E_2$ be a separation, that is,
$E_1,E_2$ be a separation, that is, ![]() $E_1\cup E_2=E$ and
$E_1\cup E_2=E$ and ![]() $r_{d-1}(E_1)+r_{d-1}(E_2)=r_{d-1}(E)$.
$r_{d-1}(E_1)+r_{d-1}(E_2)=r_{d-1}(E)$.
Let ![]() $(G,p_i)$ be the
$(G,p_i)$ be the ![]() $(d-1)$-dimensional realization of G obtained from
$(d-1)$-dimensional realization of G obtained from ![]() $(G,p)$ by a projection along the i-axis for
$(G,p)$ by a projection along the i-axis for ![]() $1\leq i\leq d$. These projected frameworks are also generic in
$1\leq i\leq d$. These projected frameworks are also generic in ![]() $\mathbb {R}^{d-1}$, and
$\mathbb {R}^{d-1}$, and ![]() $\omega $ is a stress on each
$\omega $ is a stress on each ![]() $(G,p_i)$. Let
$(G,p_i)$. Let ![]() $R(G,p_i)$ be the matrix obtained from the rigidity matrix of
$R(G,p_i)$ be the matrix obtained from the rigidity matrix of ![]() $(G,p)$ by replacing the
$(G,p)$ by replacing the ![]() $|V|$ columns corresponding to coordinate i by all-zero columns. Thus, the rigidity matrix of
$|V|$ columns corresponding to coordinate i by all-zero columns. Thus, the rigidity matrix of ![]() $(G,p_i)$ can be obtained from
$(G,p_i)$ can be obtained from ![]() $R(G,p_i)$ by removing these zero columns.
$R(G,p_i)$ by removing these zero columns.
Since ![]() $E_1,E_2$ is a separation, we must have
$E_1,E_2$ is a separation, we must have ![]() $\sum _{e\in E_1} \omega _e R_e(G,p_i)=0$ for all
$\sum _{e\in E_1} \omega _e R_e(G,p_i)=0$ for all ![]() $1\leq i\leq d+1$, where
$1\leq i\leq d+1$, where ![]() $R_e(G,p_i)$ is the row of the edge e in
$R_e(G,p_i)$ is the row of the edge e in ![]() $R(G,p_i)$. This gives
$R(G,p_i)$. This gives
 $$ \begin{align*} (d-1) \sum_{e\in E_1} \omega_e R_e(G,p) = \sum_{i=1}^{d} \sum_{e\in E_1} \omega_e R_e(G,p_i) = 0, \end{align*} $$
$$ \begin{align*} (d-1) \sum_{e\in E_1} \omega_e R_e(G,p) = \sum_{i=1}^{d} \sum_{e\in E_1} \omega_e R_e(G,p_i) = 0, \end{align*} $$implying that the restriction of ![]() $\omega $ to
$\omega $ to ![]() $E_2$ is a nonzero stress on a proper subframework of
$E_2$ is a nonzero stress on a proper subframework of ![]() $(G,p)$. Then extending this restricted stress to all of E by setting it zero on every
$(G,p)$. Then extending this restricted stress to all of E by setting it zero on every ![]() $e \in E_2$ gives another stress of
$e \in E_2$ gives another stress of ![]() $(G,p)$, contradicting the uniqueness of
$(G,p)$, contradicting the uniqueness of ![]() $\omega $.
$\omega $.
Our next result is a characterization of ![]() $\mathcal {R}_d$-connected cone graphs. We shall use the fact that G is an
$\mathcal {R}_d$-connected cone graphs. We shall use the fact that G is an ![]() $\mathcal {R}_d$-circuit if and only if
$\mathcal {R}_d$-circuit if and only if ![]() $G^v$ is an
$G^v$ is an ![]() $\mathcal {R}_{d+1}$-circuit. Although this result seems to be folklore, we could not find any proofs in the literature, so we provide one (due to W. Whiteley [Reference Whiteley24]) for completeness. For this, we shall need the following geometric result about coning, which is implicit in the work of Whiteley [Reference Whiteley22] (see also [Reference Schulze and Whiteley20, Theorem 3]).
$\mathcal {R}_{d+1}$-circuit. Although this result seems to be folklore, we could not find any proofs in the literature, so we provide one (due to W. Whiteley [Reference Whiteley24]) for completeness. For this, we shall need the following geometric result about coning, which is implicit in the work of Whiteley [Reference Whiteley22] (see also [Reference Schulze and Whiteley20, Theorem 3]).
Theorem 5.2. Let ![]() $d \geq 1$, and let
$d \geq 1$, and let ![]() $G = (V,E)$ be a graph. Let
$G = (V,E)$ be a graph. Let ![]() $(G^v,p)$ be a realization of the cone graph
$(G^v,p)$ be a realization of the cone graph ![]() $G^v$ in
$G^v$ in ![]() $\mathbb {R}^{d+1}$, and let
$\mathbb {R}^{d+1}$, and let ![]() $H \subseteq \mathbb {R}^{d+1}$ be a hyperplane not containing
$H \subseteq \mathbb {R}^{d+1}$ be a hyperplane not containing ![]() $p(v)$ and not parallel to any of the lines
$p(v)$ and not parallel to any of the lines ![]() $\overline {p(v)p(u)}, u \in V$. Finally, let
$\overline {p(v)p(u)}, u \in V$. Finally, let ![]() $(G,p_H)$ be a framework in
$(G,p_H)$ be a framework in ![]() $\mathbb {R}^d$ obtained by projecting
$\mathbb {R}^d$ obtained by projecting ![]() $p(u),u \in V$ onto H from
$p(u),u \in V$ onto H from ![]() $p(v)$ and then identifying H with
$p(v)$ and then identifying H with ![]() $\mathbb {R}^d$. Then the following holds:
$\mathbb {R}^d$. Then the following holds:
This also implies that
Lemma 5.3. Let ![]() $d \geq 1$, and let G be a graph and
$d \geq 1$, and let G be a graph and ![]() $G^v$ its cone graph. Then G is an
$G^v$ its cone graph. Then G is an ![]() $\mathcal {R}_d$-circuit if and only if
$\mathcal {R}_d$-circuit if and only if ![]() $G^v$ is an
$G^v$ is an ![]() $\mathcal {R}_{d+1}$-circuit.
$\mathcal {R}_{d+1}$-circuit.
Proof. If ![]() $G^v$ is an
$G^v$ is an ![]() $\mathcal {R}_{d+1}$-circuit, then by Theorem 2.4(a) G is not
$\mathcal {R}_{d+1}$-circuit, then by Theorem 2.4(a) G is not ![]() $\mathcal {R}_d$-independent. On the other hand, for every edge
$\mathcal {R}_d$-independent. On the other hand, for every edge ![]() $uw \in E(G)$ we have that
$uw \in E(G)$ we have that ![]() $(G - uw)^v = G^v - uw$ is
$(G - uw)^v = G^v - uw$ is ![]() $\mathcal {R}_{d+1}$-independent, so by the same theorem
$\mathcal {R}_{d+1}$-independent, so by the same theorem ![]() $G - uw$ is
$G - uw$ is ![]() $\mathcal {R}_d$-independent. This shows that G is an
$\mathcal {R}_d$-independent. This shows that G is an ![]() $\mathcal {R}_d$-circuit, as desired.
$\mathcal {R}_d$-circuit, as desired.
Now let G be an ![]() $\mathcal {R}_d$-circuit. Again by Theorem 2.4(a),
$\mathcal {R}_d$-circuit. Again by Theorem 2.4(a), ![]() $r_{d+1}(G^v) = |E(G^v)| - 1 = r_{d+1}(G^v - uw)$ for any edge
$r_{d+1}(G^v) = |E(G^v)| - 1 = r_{d+1}(G^v - uw)$ for any edge ![]() $uw \in E(G)$. Thus, we only need to prove that
$uw \in E(G)$. Thus, we only need to prove that ![]() $r_{d+1}(G^v - uv) = r_{d+1}(G^v)$ for any edge
$r_{d+1}(G^v - uv) = r_{d+1}(G^v)$ for any edge ![]() $uv$ incident to the cone vertex.
$uv$ incident to the cone vertex.
Let ![]() $uv \in E(G^v)$ be such an edge and consider a framework
$uv \in E(G^v)$ be such an edge and consider a framework ![]() $(G^v,p)$ in which the vertices of G lie in the
$(G^v,p)$ in which the vertices of G lie in the ![]() $x_{d+1} = 0$ hyperplane in a generic position (when viewed as a framework in
$x_{d+1} = 0$ hyperplane in a generic position (when viewed as a framework in ![]() $\mathbb {R}^d$) and
$\mathbb {R}^d$) and ![]() $p(v)$ lies outside of this hyperplane. Let w be a neighbour of u in G. Theorem 5.2 and the fact that the subframework
$p(v)$ lies outside of this hyperplane. Let w be a neighbour of u in G. Theorem 5.2 and the fact that the subframework ![]() $(G,p|_{V(G)})$ is generic imply that
$(G,p|_{V(G)})$ is generic imply that
Consider a framework ![]() $(G,q)$ obtained from
$(G,q)$ obtained from ![]() $(G,p)$ by changing the last coordinate of
$(G,p)$ by changing the last coordinate of ![]() $p(w)$ by a sufficiently small amount so that
$p(w)$ by a sufficiently small amount so that ![]() $\operatorname {\mathrm {rank}}(R(G^v - uw,q)) = r_{d+1}(G^v) = \operatorname {\mathrm {rank}}(R(G^v,q))$ still holds. Then there is an equilibrium stress
$\operatorname {\mathrm {rank}}(R(G^v - uw,q)) = r_{d+1}(G^v) = \operatorname {\mathrm {rank}}(R(G^v,q))$ still holds. Then there is an equilibrium stress ![]() $\omega $ of
$\omega $ of ![]() $(G^v,q)$ that is nonzero on
$(G^v,q)$ that is nonzero on ![]() $uw$. This stress must be nonzero on
$uw$. This stress must be nonzero on ![]() $uv$ as well, since in this framework, the rest of the edges incident to u all lie in the
$uv$ as well, since in this framework, the rest of the edges incident to u all lie in the ![]() $x_{d+1} = 0$ hyperplane. This shows that
$x_{d+1} = 0$ hyperplane. This shows that
which implies ![]() $r_{d+1}(G^v - uv) = r_{d+1}(G^v)$, as desired.
$r_{d+1}(G^v - uv) = r_{d+1}(G^v)$, as desired.
Theorem 5.4. Let G be a graph, and let ![]() $G^v$ denote its cone graph. Then
$G^v$ denote its cone graph. Then ![]() $G^v$ is
$G^v$ is ![]() $\mathcal {R}_{d+1}$-connected if and only if G is connected and it has no
$\mathcal {R}_{d+1}$-connected if and only if G is connected and it has no ![]() $\mathcal {R}_d$-bridges.
$\mathcal {R}_d$-bridges.
Proof. For the ‘only if’ direction, observe that coning takes an ![]() $\mathcal {R}_d$-bridge of G to an
$\mathcal {R}_d$-bridge of G to an ![]() $\mathcal {R}_{d+1}$-bridge of
$\mathcal {R}_{d+1}$-bridge of ![]() $G^v$, which follows from Theorem 5.2 and that an
$G^v$, which follows from Theorem 5.2 and that an ![]() $\mathcal {R}_d$-connected graph on at least two edges has no
$\mathcal {R}_d$-connected graph on at least two edges has no ![]() $\mathcal {R}_d$-bridges. Moreover,
$\mathcal {R}_d$-bridges. Moreover, ![]() $\mathcal {R}_d$-connected graphs are
$\mathcal {R}_d$-connected graphs are ![]() $2$-connected,Footnote 5 while the cone graph of a disconnected graph is not.
$2$-connected,Footnote 5 while the cone graph of a disconnected graph is not.
To prove the ‘if’ direction, let us first observe that for any edge ![]() $xy$ of G,
$xy$ of G, ![]() $xy$ is in the same
$xy$ is in the same ![]() $\mathcal {R}_{d+1}$-connected component of
$\mathcal {R}_{d+1}$-connected component of ![]() $G^v$ as
$G^v$ as ![]() $vx$ and
$vx$ and ![]() $vy$. Indeed, since
$vy$. Indeed, since ![]() $xy$ is not an
$xy$ is not an ![]() $\mathcal {R}_d$-bridge in G, it is contained in some subgraph of G that is an
$\mathcal {R}_d$-bridge in G, it is contained in some subgraph of G that is an ![]() $\mathcal {R}_d$-circuit, and by Lemma 5.3, the cone of this subgraph is an
$\mathcal {R}_d$-circuit, and by Lemma 5.3, the cone of this subgraph is an ![]() $\mathcal {R}_{d+1}$-circuit which contains all three of these edges.
$\mathcal {R}_{d+1}$-circuit which contains all three of these edges.
Thus, it is sufficient to prove that any pair of cone edges ![]() $vx, vy$ is in the same
$vx, vy$ is in the same ![]() $\mathcal {R}_{d+1}$-connected component of
$\mathcal {R}_{d+1}$-connected component of ![]() $G^v$. By assumption, there is a path
$G^v$. By assumption, there is a path ![]() $x = u_0,u_1,\dots ,u_k = y$ in G. Now by the previous observation
$x = u_0,u_1,\dots ,u_k = y$ in G. Now by the previous observation ![]() $vu_i$ and
$vu_i$ and ![]() $vu_{i+1}$ are in the same
$vu_{i+1}$ are in the same ![]() $\mathcal {R}_{d+1}$-connected component of
$\mathcal {R}_{d+1}$-connected component of ![]() $G^v$, for all
$G^v$, for all ![]() $0 \leq i < k$. By transitivity, we get that
$0 \leq i < k$. By transitivity, we get that ![]() $vx$ and
$vx$ and ![]() $vy$ are also in the same
$vy$ are also in the same ![]() $\mathcal {R}_{d+1}$-connected component, as desired.
$\mathcal {R}_{d+1}$-connected component, as desired.
For a graph ![]() $G=(V,E)$ let
$G=(V,E)$ let ![]() $\operatorname {\mathrm {dof}}_d(G)=d|V|-\binom {d+1}{2}-r_d(G)$ denote its ‘degrees of freedom’ in the context of d-dimensional generic rigidity. The next theorem verifies a general combinatorial property of highly connected
$\operatorname {\mathrm {dof}}_d(G)=d|V|-\binom {d+1}{2}-r_d(G)$ denote its ‘degrees of freedom’ in the context of d-dimensional generic rigidity. The next theorem verifies a general combinatorial property of highly connected ![]() $\mathcal {R}_d$-separable graphs and may be useful in the construction of further families of examples.
$\mathcal {R}_d$-separable graphs and may be useful in the construction of further families of examples.
Theorem 5.5. Let ![]() $d \geq 1$, and let G be a
$d \geq 1$, and let G be a ![]() $(d+1)$-connected and redundantly rigid graph in
$(d+1)$-connected and redundantly rigid graph in ![]() $\mathbb {R}^d$. Suppose that G is
$\mathbb {R}^d$. Suppose that G is ![]() $\mathcal {R}_d$-separable, and let
$\mathcal {R}_d$-separable, and let ![]() $H_1$,
$H_1$, ![]() $H_2$,…,
$H_2$,…,![]() $H_q$ be the
$H_q$ be the ![]() $\mathcal {R}_d$-connected components of G. Then
$\mathcal {R}_d$-connected components of G. Then
 $$ \begin{align*} \sum_{i=1}^q \operatorname{\mathrm{dof}}_d(H_i) \geq \binom{d+1}{2}. \end{align*} $$
$$ \begin{align*} \sum_{i=1}^q \operatorname{\mathrm{dof}}_d(H_i) \geq \binom{d+1}{2}. \end{align*} $$Proof. Let ![]() $X_i=V(H_i)-\cup _{j\not = i}V(H_j)$ denote the set of vertices belonging to no other
$X_i=V(H_i)-\cup _{j\not = i}V(H_j)$ denote the set of vertices belonging to no other ![]() $\mathcal {R}_d$-connected component than
$\mathcal {R}_d$-connected component than ![]() $H_i$, and let
$H_i$, and let ![]() $Y_i=V(H_i)-X_i$ for
$Y_i=V(H_i)-X_i$ for ![]() $1\leq i\leq q$. Let
$1\leq i\leq q$. Let ![]() $n_i=|V(H_i)|$,
$n_i=|V(H_i)|$, ![]() $x_i=|X_i|$,
$x_i=|X_i|$, ![]() $y_i=|Y_i|$. Clearly,
$y_i=|Y_i|$. Clearly, ![]() $n_i=x_i+y_i$ and
$n_i=x_i+y_i$ and ![]() $|V|=\sum _{i=1}^q x_i + |\cup _{i=1}^q Y_i|$. Moreover, we have
$|V|=\sum _{i=1}^q x_i + |\cup _{i=1}^q Y_i|$. Moreover, we have ![]() $\sum _{i=1}^q y_i \geq 2|\cup _{i=1}^q Y_i|$. Since G is redundantly rigid, every edge of G is in some
$\sum _{i=1}^q y_i \geq 2|\cup _{i=1}^q Y_i|$. Since G is redundantly rigid, every edge of G is in some ![]() $\mathcal {R}_d$-circuit. Every
$\mathcal {R}_d$-circuit. Every ![]() $\mathcal {R}_d$-circuit has at least
$\mathcal {R}_d$-circuit has at least ![]() $d+2$ vertices. Thus we have that
$d+2$ vertices. Thus we have that ![]() $n_i\geq d+2$ for
$n_i\geq d+2$ for ![]() $1\leq i\leq q$. Furthermore, since G is
$1\leq i\leq q$. Furthermore, since G is ![]() $(d+1)$-connected,
$(d+1)$-connected, ![]() $y_i\geq (d+1)$ holds for all
$y_i\geq (d+1)$ holds for all ![]() $\mathcal {R}_d$-components.
$\mathcal {R}_d$-components.
Let us choose a base ![]() $B_i$ in each rigidity matroid
$B_i$ in each rigidity matroid ![]() ${\mathcal{R}}(H_i)$. Using the above inequalities, we have
${\mathcal{R}}(H_i)$. Using the above inequalities, we have
 $$ \begin{align*} d|V|-\binom{d+1}{2}&= |\cup_{i=1}^q B_i|=\sum_{i=1}^q |B_i| =\sum_{i=1}^q \left(dn_i-\binom{d+1}{2}-\operatorname{\mathrm{dof}}_d(H_i)\right) \\ &=d\sum_{i=1}^q n_i - \binom{d+1}{2}q - \sum_{i=1}^q \operatorname{\mathrm{dof}}_d(H_i) \\ &=\left(d\sum_{i=1}^q x_i + \frac{d}{2}\sum_{i=1}^q y_i\right) + \left(\frac{d}{2}\sum_{i=1}^q y_i-\binom{d+1}{2}q\right) - \sum_{i=1}^q \operatorname{\mathrm{dof}}_d(H_i) \\ &\geq d|V| - \sum_{i=1}^q \operatorname{\mathrm{dof}}_d(H_i) \end{align*} $$
$$ \begin{align*} d|V|-\binom{d+1}{2}&= |\cup_{i=1}^q B_i|=\sum_{i=1}^q |B_i| =\sum_{i=1}^q \left(dn_i-\binom{d+1}{2}-\operatorname{\mathrm{dof}}_d(H_i)\right) \\ &=d\sum_{i=1}^q n_i - \binom{d+1}{2}q - \sum_{i=1}^q \operatorname{\mathrm{dof}}_d(H_i) \\ &=\left(d\sum_{i=1}^q x_i + \frac{d}{2}\sum_{i=1}^q y_i\right) + \left(\frac{d}{2}\sum_{i=1}^q y_i-\binom{d+1}{2}q\right) - \sum_{i=1}^q \operatorname{\mathrm{dof}}_d(H_i) \\ &\geq d|V| - \sum_{i=1}^q \operatorname{\mathrm{dof}}_d(H_i) \end{align*} $$Thus, we must have ![]() $\sum _{i=1}^q \operatorname {\mathrm {dof}}_d(H_i) \geq \binom {d+1}{2}$, as claimed.
$\sum _{i=1}^q \operatorname {\mathrm {dof}}_d(H_i) \geq \binom {d+1}{2}$, as claimed.
The graph of Figure 2 shows that Theorem 5.5 is, in some sense, tight: It has a unique nonrigid ![]() $\mathcal {R}_3$-connected component with six degrees of freedom. Note that for
$\mathcal {R}_3$-connected component with six degrees of freedom. Note that for ![]() $d=1,2$ the
$d=1,2$ the ![]() $\mathcal {R}_d$-connected components of a graph are rigid. Thus, the theorem implies that for
$\mathcal {R}_d$-connected components of a graph are rigid. Thus, the theorem implies that for ![]() $d\leq 2$ the
$d\leq 2$ the ![]() $(d+1)$-connected redundantly rigid graphs are
$(d+1)$-connected redundantly rigid graphs are ![]() $\mathcal {R}_d$-connected, which was shown in [Reference Jackson and Jordán14, Theorem 3.2] by a similar argument.
$\mathcal {R}_d$-connected, which was shown in [Reference Jackson and Jordán14, Theorem 3.2] by a similar argument.
Acknowledgements
This work was supported by the Hungarian Scientific Research Fund grant no. K 135421 and the project Application Domain Specific Highly Reliable IT Solutions which has been implemented with the support provided from the National Research, Development and Innovation Fund of Hungary, financed under the Thematic Excellence Programme TKP2020-NKA-06 (National Challenges Subprogramme) funding scheme.
Conflicts of Interest
None.