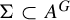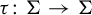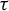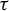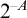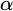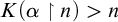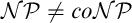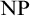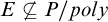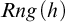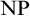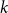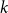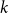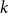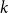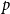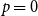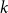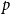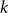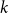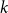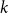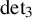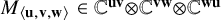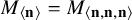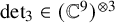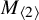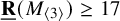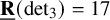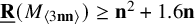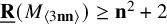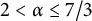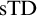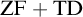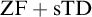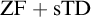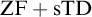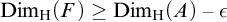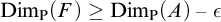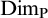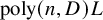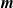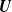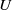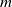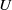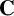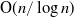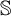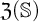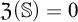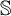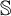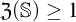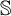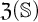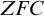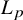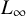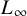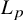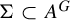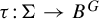102 results in 68Qxx
Binary pattern retrieval with Kuramoto-type oscillators via a least orthogonal lift of three patterns
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 16 May 2024, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE FRAGILITY OF INTERPOLATION
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 21 March 2024, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant sets and nilpotency of endomorphisms of algebraic sofic shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 15 February 2024, pp. 1-42
-
- Article
- Export citation
REGAININGLY APPROXIMABLE NUMBERS AND SETS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 22 January 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zeros, chaotic ratios and the computational complexity of approximating the independence polynomial
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 24 November 2023, pp. 459-494
- Print publication:
- March 2024
-
- Article
- Export citation
ON THE EXISTENCE OF STRONG PROOF COMPLEXITY GENERATORS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 22 November 2023, pp. 20-40
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A PROOF COMPLEXITY CONJECTURE AND THE INCOMPLETENESS THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 19 September 2023, pp. 1-5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Phase transition for the generalized two-community stochastic block model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 31 July 2023, pp. 385-400
- Print publication:
- June 2024
-
- Article
- Export citation
Polarised random
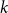 $k$-SAT
$k$-SAT
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 20 July 2023, pp. 885-899
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
New lower bounds for matrix multiplication and
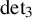 $\operatorname {det}_3$
$\operatorname {det}_3$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 29 May 2023, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The first-order theory of binary overlap-free words is decidable
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 26 May 2023, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stable finiteness of twisted group rings and noisy linear cellular automata
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 22 May 2023, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOME CONSEQUENCES OF
 ${\mathrm {TD}}$ AND
${\mathrm {TD}}$ AND 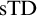 ${\mathrm {sTD}}$
${\mathrm {sTD}}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1573-1589
- Print publication:
- December 2023
-
- Article
- Export citation
Rigid continuation paths II. structured polynomial systems
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 14 April 2023, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic normality for
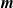 $\boldsymbol{m}$-dependent and constrained
$\boldsymbol{m}$-dependent and constrained 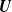 $\boldsymbol{U}$-statistics, with applications to pattern matching in random strings and permutations
$\boldsymbol{U}$-statistics, with applications to pattern matching in random strings and permutations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 28 March 2023, pp. 841-894
- Print publication:
- September 2023
-
- Article
- Export citation
MULTIPLICATION TABLES AND WORD-HYPERBOLICITY IN FREE PRODUCTS OF SEMIGROUPS, MONOIDS AND GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 17 March 2023, pp. 396-430
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An efficient method for generating a discrete uniform distribution using a biased random source
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 07 March 2023, pp. 1069-1078
- Print publication:
- September 2023
-
- Article
- Export citation
THE ZHOU ORDINAL OF LABELLED MARKOV PROCESSES OVER SEPARABLE SPACES
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 27 February 2023, pp. 1011-1032
- Print publication:
- December 2023
-
- Article
- Export citation
Functional norms, condition numbers and numerical algorithms in algebraic geometry
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 22 November 2022, e103
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On images of subshifts under embeddings of symbolic varieties
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 01 August 2022, pp. 3131-3149
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation