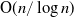1. Background
Sampling a target distribution from a random physical source has many applications. However, the random physical sources are often biased with unknown distribution, while we need a specific target distribution in applications. Therefore, an efficient algorithm to generate a target distribution from a random source is of great value. A simple method to generate a fair binary distribution from an unfair binary source with an unknown bias was first proposed in [Reference Von Neumann7], and this method has served as a precursor of a series of algorithms to generate a target distribution from an unknown random source.
Von Neumann’s method was improved in [Reference Hoeffding and Simons3, Reference Stout and Warren6] to generate a fair binary distribution from a biased random source. From the point of view of probability theory, [Reference Elias2] formally defined the kind of random procedure that can generate a target distribution. Elias also designed an infinite sequence of sampling schemes, with computational efficiency decreasing to the theoretical lower bound, though without providing an executable algorithm for the method. Elias’ method needs to generate Elias’ function first; such a preprocessing step needs an exponential space cost and at least a polynomial time cost [Reference Pae5], and thus Elias’ method is computationally costly and inefficient.
Another method, for generating a uniform distribution on a set of p elements for p prime, was provided in [Reference Dijkstra1], though Dijkstra’s method is computationally inefficient. Indeed, in realizing this method we need a preprocessing step to generate and store a function which maps outcomes from the random source to some target values. However, such a preprocessing step needs an exponential time and space cost.
In this article we propose a new algorithm based on the idea of Dijkstra’s method. The proposed algorithm does not need a preprocessing step, and is thus computationally efficient. The article is organized as follows: In Section 2, we briefly recast Von Neumann’s method as a starting point, as well as a special case of our algorithm. In Section 3, we heuristically construct and explain our algorithm. In Sections 4 and 5 we formally propose our algorithms and verify them theoretically. In Section 5, we prove that our algorithm has overall sublinear average running time. Another novel proof of Theorem 1 is given in Appendix A.
2. Introduction to Von Neumann’s method
Let
![]() $X\in \{ H, T \}$
denote the outcome of a biased coin flip with probability
$X\in \{ H, T \}$
denote the outcome of a biased coin flip with probability
![]() $a=\mathbb{P}(X=H)\in (0,1)$
of getting a head and probability
$a=\mathbb{P}(X=H)\in (0,1)$
of getting a head and probability
![]() $b=\mathbb{P}(X=T)=1-a$
of getting a tail. Let
$b=\mathbb{P}(X=T)=1-a$
of getting a tail. Let
![]() $\{X_i\;:\; i\ge 0\}$
be independent and identically distributed (i.i.d.) copies of X. Von Neumann proposed an algorithm
$\{X_i\;:\; i\ge 0\}$
be independent and identically distributed (i.i.d.) copies of X. Von Neumann proposed an algorithm
![]() $\mathcal{A}_1$
to generate a fair binary random variable with distribution
$\mathcal{A}_1$
to generate a fair binary random variable with distribution
![]() $\mathbb{P}(\mathcal{A}_1=0)=\mathbb{P}(\mathcal{A}_1=1)=\frac12$
as shown in Algorithm 1 [Reference Von Neumann7].
$\mathbb{P}(\mathcal{A}_1=0)=\mathbb{P}(\mathcal{A}_1=1)=\frac12$
as shown in Algorithm 1 [Reference Von Neumann7].
Let
![]() $\{ {\boldsymbol{{Y}}}_i = (X_{2i}, X_{2i+1})\;:\; i \ge 0 \}$
be i.i.d. outcomes of pairs of flips, and
$\{ {\boldsymbol{{Y}}}_i = (X_{2i}, X_{2i+1})\;:\; i \ge 0 \}$
be i.i.d. outcomes of pairs of flips, and
![]() $\tau$
be the first time that
$\tau$
be the first time that
![]() ${\boldsymbol{{Y}}}_i \in \{ HT, TH \}$
; then
${\boldsymbol{{Y}}}_i \in \{ HT, TH \}$
; then
This derivation shows that
![]() $\mathcal{A}_1$
generates a fair binary distribution. Below, we propose an efficient algorithm to generate a uniform distribution on p elements for p prime. At each cycle we flip a coin p times; the algorithm returns a number in
$\mathcal{A}_1$
generates a fair binary distribution. Below, we propose an efficient algorithm to generate a uniform distribution on p elements for p prime. At each cycle we flip a coin p times; the algorithm returns a number in
![]() $\{ 0, \ldots, p-1 \}$
except when the p flips are all heads or all tails, analogous to Von Neumann’s method.
$\{ 0, \ldots, p-1 \}$
except when the p flips are all heads or all tails, analogous to Von Neumann’s method.
Algorithm 1
![]() $\mathcal{A}_{\textbf{1}}$
: Von Neumann’s algorithm generating a fair binary random variable.
$\mathcal{A}_{\textbf{1}}$
: Von Neumann’s algorithm generating a fair binary random variable.

3. Heuristic explanation for the main idea
Let the random vector
![]() ${\boldsymbol{{X}}}^{n}= ( X_0, \ldots, X_{n-1} )\in \{H, T \}^n$
be the outcome of n flips. Let
${\boldsymbol{{X}}}^{n}= ( X_0, \ldots, X_{n-1} )\in \{H, T \}^n$
be the outcome of n flips. Let
![]() $N_{\text{head}}({\boldsymbol{{X}}}^{n})$
denote the head count in
$N_{\text{head}}({\boldsymbol{{X}}}^{n})$
denote the head count in
![]() ${\boldsymbol{{X}}}^{n}$
, and
${\boldsymbol{{X}}}^{n}$
, and
![]() $S_{\text{head}}({\boldsymbol{{X}}}^{n})$
denote the rank sum of heads in
$S_{\text{head}}({\boldsymbol{{X}}}^{n})$
denote the rank sum of heads in
![]() ${\boldsymbol{{X}}}^{n}$
, with rank beginning from 0:
${\boldsymbol{{X}}}^{n}$
, with rank beginning from 0:
 \begin{equation} N_{\text{head}}({\boldsymbol{{X}}}^{n})=\sum_{i=0}^{n-1}\mathbf{1}_{\{X_i = H \}} , \qquad S_{\text{head}}({\boldsymbol{{X}}}^{n})=\sum_{i=0}^{n-1} i\cdot \mathbf{1}_{\{X_i = H \}}.\end{equation}
\begin{equation} N_{\text{head}}({\boldsymbol{{X}}}^{n})=\sum_{i=0}^{n-1}\mathbf{1}_{\{X_i = H \}} , \qquad S_{\text{head}}({\boldsymbol{{X}}}^{n})=\sum_{i=0}^{n-1} i\cdot \mathbf{1}_{\{X_i = H \}}.\end{equation}
For example, when
![]() ${\boldsymbol{{X}}}^{5}=(H,H,T,H,T)$
, we have
${\boldsymbol{{X}}}^{5}=(H,H,T,H,T)$
, we have
![]() $N_{\text{head}}({\boldsymbol{{X}}}^{5})=3$
and
$N_{\text{head}}({\boldsymbol{{X}}}^{5})=3$
and
![]() $S_{\text{head}}({\boldsymbol{{X}}}^{5})=4.$
$S_{\text{head}}({\boldsymbol{{X}}}^{5})=4.$
For a specific sequence of n flips
![]() ${\boldsymbol{{x}}}^n=(x_0,\ldots, x_{n-1})\in \{H, T \}^n$
as an observation of
${\boldsymbol{{x}}}^n=(x_0,\ldots, x_{n-1})\in \{H, T \}^n$
as an observation of
![]() ${\boldsymbol{{X}}}^{n}$
, if
${\boldsymbol{{X}}}^{n}$
, if
![]() $N_{\text{head}}({\boldsymbol{{x}}}^n)=\sum_{i=0}^{n-1}\mathbf{1}_{\{x_i=H\}}=k$
, then the probability of getting
$N_{\text{head}}({\boldsymbol{{x}}}^n)=\sum_{i=0}^{n-1}\mathbf{1}_{\{x_i=H\}}=k$
, then the probability of getting
![]() ${\boldsymbol{{x}}}^n$
in n flips is
${\boldsymbol{{x}}}^n$
in n flips is
![]() $\mathbb{P}({\boldsymbol{{X}}}^{n} = {\boldsymbol{{x}}}^n) = \prod_{i=0}^{n-1}\mathbb{P}(X_i = x_i)=a^k b^{n-k}$
, which only depends on the head count k. As a result, for
$\mathbb{P}({\boldsymbol{{X}}}^{n} = {\boldsymbol{{x}}}^n) = \prod_{i=0}^{n-1}\mathbb{P}(X_i = x_i)=a^k b^{n-k}$
, which only depends on the head count k. As a result, for
![]() $0\le k\le n$
, there are exactly
$0\le k\le n$
, there are exactly
![]() $\binom{n}{k}$
outcomes of n flips containing k heads, each with the same probability
$\binom{n}{k}$
outcomes of n flips containing k heads, each with the same probability
![]() $a^k b^{n-k}$
. Let
$a^k b^{n-k}$
. Let
where
![]() $|A|$
means the cardinality of set A. Thus,
$|A|$
means the cardinality of set A. Thus,
![]() $S_k$
is the set of all subsets of
$S_k$
is the set of all subsets of
![]() $\{ 0, \ldots, n\!-\!1 \}$
containing k elements. Note that
$\{ 0, \ldots, n\!-\!1 \}$
containing k elements. Note that
![]() $|S_k|=\binom{n}{k}$
, and each element in
$|S_k|=\binom{n}{k}$
, and each element in
![]() $S_k$
corresponds to one and only one outcome of n flips with k heads in the following way:
$S_k$
corresponds to one and only one outcome of n flips with k heads in the following way:
where each
![]() $i_t$
corresponds to the rank of an appearance of a head in the
$i_t$
corresponds to the rank of an appearance of a head in the
![]() $i_t$
th flip of n,
$i_t$
th flip of n,
![]() $i_1 < i_2 <\cdots <i_k$
. As a result, we have the one-to-one correspondence
$i_1 < i_2 <\cdots <i_k$
. As a result, we have the one-to-one correspondence
and we also have
![]() $\mathbb{P}({\boldsymbol{{X}}}^{n} = {\boldsymbol{{x}}}^n)=a^{k}b^{n-k}$
for all
$\mathbb{P}({\boldsymbol{{X}}}^{n} = {\boldsymbol{{x}}}^n)=a^{k}b^{n-k}$
for all
![]() ${\boldsymbol{{x}}}^n \in S_k$
. Note that in the correspondences (3) and (4) we do not distinguish the left- and right-hand sides in the derivation below. And the equivalences are frequently used in the following proof.
${\boldsymbol{{x}}}^n \in S_k$
. Note that in the correspondences (3) and (4) we do not distinguish the left- and right-hand sides in the derivation below. And the equivalences are frequently used in the following proof.
Algorithm 2
![]() $\mathcal{A}$
: Generating a discrete distribution on the set
$\mathcal{A}$
: Generating a discrete distribution on the set
![]() $\{0, \ldots, n\!-\!1 \}$
.
$\{0, \ldots, n\!-\!1 \}$
.

Inspired by Von Neumann’s algorithm, we consider an algorithm generating a distribution on the set
![]() $\{ 0, \ldots, n\!-\!1 \}$
. At each cycle we flip the coin n times, then the algorithm returns a number in
$\{ 0, \ldots, n\!-\!1 \}$
. At each cycle we flip the coin n times, then the algorithm returns a number in
![]() $\{ 0, \ldots, n\!-\!1 \}$
except when the outcome is all heads or all tails. Define the sets
$\{ 0, \ldots, n\!-\!1 \}$
except when the outcome is all heads or all tails. Define the sets
![]() $\{ A_m \;:\; 0\le m\le n\!-\!1\}$
to be a disjoint partition of
$\{ A_m \;:\; 0\le m\le n\!-\!1\}$
to be a disjoint partition of
![]() $\bigsqcup_{1\le k\le n\!-\!1}S_k$
,
$\bigsqcup_{1\le k\le n\!-\!1}S_k$
,
 \begin{equation*} \bigsqcup_{k=1}^{n-1}S_k = \bigsqcup_{m=0}^{n-1}A_m,\end{equation*}
\begin{equation*} \bigsqcup_{k=1}^{n-1}S_k = \bigsqcup_{m=0}^{n-1}A_m,\end{equation*}
where
![]() $\bigsqcup$
means disjoint union. The algorithm,
$\bigsqcup$
means disjoint union. The algorithm,
![]() $\mathcal{A}$
, is formally stated in Algorithm 2.
$\mathcal{A}$
, is formally stated in Algorithm 2.
Let
![]() $\{{\boldsymbol{{Y}}}_i = (X_{in}, \ldots, X_{in+n\!-\!1})\;:\; i\ge 0\}$
be i.i.d. outcomes of n flips, and
$\{{\boldsymbol{{Y}}}_i = (X_{in}, \ldots, X_{in+n\!-\!1})\;:\; i\ge 0\}$
be i.i.d. outcomes of n flips, and
![]() $\tau$
be the first time
$\tau$
be the first time
![]() ${\boldsymbol{{Y}}}_i$
is neither all heads nor all tails. Then, for
${\boldsymbol{{Y}}}_i$
is neither all heads nor all tails. Then, for
![]() $0 \le m \le n\!-\!1$
, we have
$0 \le m \le n\!-\!1$
, we have
 \begin{align} \mathbb{P}(\mathcal{A}=m) & = \mathbb{P}({\boldsymbol{{Y}}}_\tau \in A_m) \notag \\[5pt] & = \frac{\mathbb{P}({\boldsymbol{{X}}}^{n} \in A_m)} {\mathbb{P}({\boldsymbol{{X}}}^{n} \in S_k \text{ for some } 1\le k\le n\!-\!1)} \notag \\[5pt] & = \frac{\sum_{k=1}^{n-1} \mathbb{P} ({\boldsymbol{{X}}}^{n} \in A_m\cap S_k)} {\sum_{k=1}^{n-1} \mathbb{P} ({\boldsymbol{{X}}}^{n} \in S_k) } = \frac{\sum_{k=1}^{n-1} |A_m \cap S_k| a^k b^{n-k} }{\sum_{k=1}^{n-1} |S_k| a^k b^{n-k} }.\end{align}
\begin{align} \mathbb{P}(\mathcal{A}=m) & = \mathbb{P}({\boldsymbol{{Y}}}_\tau \in A_m) \notag \\[5pt] & = \frac{\mathbb{P}({\boldsymbol{{X}}}^{n} \in A_m)} {\mathbb{P}({\boldsymbol{{X}}}^{n} \in S_k \text{ for some } 1\le k\le n\!-\!1)} \notag \\[5pt] & = \frac{\sum_{k=1}^{n-1} \mathbb{P} ({\boldsymbol{{X}}}^{n} \in A_m\cap S_k)} {\sum_{k=1}^{n-1} \mathbb{P} ({\boldsymbol{{X}}}^{n} \in S_k) } = \frac{\sum_{k=1}^{n-1} |A_m \cap S_k| a^k b^{n-k} }{\sum_{k=1}^{n-1} |S_k| a^k b^{n-k} }.\end{align}
Let us consider a special case of algorithm
![]() $\mathcal{A}$
where n is a prime, p. The reason for focusing on prime p comes from the fact in number theory that
$\mathcal{A}$
where n is a prime, p. The reason for focusing on prime p comes from the fact in number theory that
![]() $p \mid \binom{p}{k} = |S_k|$
for all
$p \mid \binom{p}{k} = |S_k|$
for all
![]() $1\le k\le p-1$
, where the symbol
$1\le k\le p-1$
, where the symbol
![]() $|$
means ‘divides’. Then, for each k, we can partition
$|$
means ‘divides’. Then, for each k, we can partition
![]() $S_k$
into disjoint p parts of equal size. For
$S_k$
into disjoint p parts of equal size. For
![]() $1\le k \le p-1$
, assume that the choice of sets
$1\le k \le p-1$
, assume that the choice of sets
![]() $\{ A_m\;:\; 0 \le m \le p-1 \}$
satisfies
$\{ A_m\;:\; 0 \le m \le p-1 \}$
satisfies
where the disjoint
![]() $\{ A_m \cap S_k\;:\; 0\le m\le p-1 \}$
partition
$\{ A_m \cap S_k\;:\; 0\le m\le p-1 \}$
partition
![]() $S_k$
into p subsets of equal size. Based on (5) and (6), for
$S_k$
into p subsets of equal size. Based on (5) and (6), for
![]() $0 \le m\le p-1$
we have
$0 \le m\le p-1$
we have
 \begin{equation*} \mathbb{P}(\mathcal{A}=m)= \frac{\sum_{k=1}^{p-1} |A_m \cap S_k| a^k b^{n-k} } {\sum_{k=1}^{p-1} |S_k| a^k b^{n-k} } = \frac{\sum_{k=1}^{p-1} \frac{1}{p}|S_k| a^k b^{n-k} }{\sum_{k=1}^{p-1} |S_k| a^k b^{n-k} } = \frac{1}{p},\end{equation*}
\begin{equation*} \mathbb{P}(\mathcal{A}=m)= \frac{\sum_{k=1}^{p-1} |A_m \cap S_k| a^k b^{n-k} } {\sum_{k=1}^{p-1} |S_k| a^k b^{n-k} } = \frac{\sum_{k=1}^{p-1} \frac{1}{p}|S_k| a^k b^{n-k} }{\sum_{k=1}^{p-1} |S_k| a^k b^{n-k} } = \frac{1}{p},\end{equation*}
which means algorithm
![]() $\mathcal{A}$
returns a uniform distribution on
$\mathcal{A}$
returns a uniform distribution on
![]() $\{ 0, \ldots, p-1 \}$
.
$\{ 0, \ldots, p-1 \}$
.
What remains is to find
![]() $\{ A_m\;:\; 0\le m\le p-1 \}$
satisfying (6). We can always first partition
$\{ A_m\;:\; 0\le m\le p-1 \}$
satisfying (6). We can always first partition
![]() $S_k$
into p subsets of equal size, and then define
$S_k$
into p subsets of equal size, and then define
![]() $\{ A_m \cap S_k\;:\; 0\le m\le p-1 \}$
to be these subsets, like the proposed method in [Reference Dijkstra1]. However, this method has two disadvantages. First, there are many ways of partitioning
$\{ A_m \cap S_k\;:\; 0\le m\le p-1 \}$
to be these subsets, like the proposed method in [Reference Dijkstra1]. However, this method has two disadvantages. First, there are many ways of partitioning
![]() $S_k$
into subsets of equal size, and there is no widely accepted standard. Second, partitioning
$S_k$
into subsets of equal size, and there is no widely accepted standard. Second, partitioning
![]() $\{S_k\;:\; 1\le k\le p-1\}$
and designing
$\{S_k\;:\; 1\le k\le p-1\}$
and designing
![]() $\{ A_m\;:\; 0\le m\le p-1 \}$
need excessive time and storage cost, because there are
$\{ A_m\;:\; 0\le m\le p-1 \}$
need excessive time and storage cost, because there are
![]() $2^p$
different outcomes of p flips we need to handle, which grows exponentially as p increases. A preprocessing step of exponential time is unacceptable for an efficient algorithm.
$2^p$
different outcomes of p flips we need to handle, which grows exponentially as p increases. A preprocessing step of exponential time is unacceptable for an efficient algorithm.
With the help of the modulo p function, there is an ingenious way of designing
![]() $\{ A_m\;:\; 0\le m\le p-1 \}$
to satisfy (6). Based on the correspondence in (3), for
$\{ A_m\;:\; 0\le m\le p-1 \}$
to satisfy (6). Based on the correspondence in (3), for
![]() $0\le m\le p-1$
we can indeed choose
$0\le m\le p-1$
we can indeed choose
as we show in the next section.
4. Generating a uniform distribution on p (prime) elements
We provide an algorithm,
![]() $\mathcal{A}_2(p)$
, that generates a discrete uniform distribution on the set
$\mathcal{A}_2(p)$
, that generates a discrete uniform distribution on the set
![]() $\{0, \ldots, p-1 \},$
where p is a prime, as listed in Algorithm 3.
$\{0, \ldots, p-1 \},$
where p is a prime, as listed in Algorithm 3.
Algorithm 3
![]() $\mathcal{A}_2(p)$
: Generating a discrete uniform distribution on
$\mathcal{A}_2(p)$
: Generating a discrete uniform distribution on
![]() $\{0, \ldots, p-1\}$
.
$\{0, \ldots, p-1\}$
.

We need the following lemma before proving the main theory.
Lemma 1. Let p be a prime number, and let
![]() $\{ S_k\;:\; 1\le k\le p-1 \}$
consist of all subsets of
$\{ S_k\;:\; 1\le k\le p-1 \}$
consist of all subsets of
![]() $\{ 0,\ldots, p-1 \}$
having k elements. For fixed k, let
$\{ 0,\ldots, p-1 \}$
having k elements. For fixed k, let
![]() $\{ S_k^m \;:\; 0\le m\le p-1 \}$
be defined by
$\{ S_k^m \;:\; 0\le m\le p-1 \}$
be defined by
 \begin{equation} S^m_k = \Bigg\{\{i_1,\ldots, i_k\}\in S_k\;:\;\sum_{j=1}^k i_j = m \,(\textrm{mod}\,p) \Bigg\}. \end{equation}
\begin{equation} S^m_k = \Bigg\{\{i_1,\ldots, i_k\}\in S_k\;:\;\sum_{j=1}^k i_j = m \,(\textrm{mod}\,p) \Bigg\}. \end{equation}
Note that
![]() $S^m_k = A_m \cap S_k$
, where
$S^m_k = A_m \cap S_k$
, where
![]() $A_m$
is defined in (7).
$A_m$
is defined in (7).
Then we have
Proof. For fixed
![]() $1\le k\le p-1$
, consider a permutation on
$1\le k\le p-1$
, consider a permutation on
![]() $S_k$
defined by
$S_k$
defined by
Denote by
![]() $f^0$
the identity function
$f^0$
the identity function
![]() $\operatorname{id}$
. Let
$\operatorname{id}$
. Let
![]() $\langle f\rangle$
be the subgroup generated by f. We need to show that
$\langle f\rangle$
be the subgroup generated by f. We need to show that
![]() $\langle f\rangle = \{f^0=\operatorname{id}, f^1,\ldots, f^{p-1}\}$
. Since we know that
$\langle f\rangle = \{f^0=\operatorname{id}, f^1,\ldots, f^{p-1}\}$
. Since we know that
![]() $f^{p}=\operatorname{id}$
, we need to show
$f^{p}=\operatorname{id}$
, we need to show
![]() $f^s\neq \operatorname{id}$
for
$f^s\neq \operatorname{id}$
for
![]() $1\le s\le p-1$
.
$1\le s\le p-1$
.
If
![]() $f^s= \operatorname{id}$
for some
$f^s= \operatorname{id}$
for some
![]() $1\le s\le p-1$
, then we have
$1\le s\le p-1$
, then we have
from which we have
![]() $\sum_{j=1}^k(i_j+s) = \sum_{j=1}^k i_j \,(\textrm{mod}\,p)$
. The equality above shows
$\sum_{j=1}^k(i_j+s) = \sum_{j=1}^k i_j \,(\textrm{mod}\,p)$
. The equality above shows
![]() $ p\mid ks$
, which implies
$ p\mid ks$
, which implies
![]() $p\mid k$
or
$p\mid k$
or
![]() $p\mid s$
, leading to a contradiction since
$p\mid s$
, leading to a contradiction since
![]() $1\le k,s \le p-1$
.
$1\le k,s \le p-1$
.
Let the group
![]() $\langle f\rangle$
act on
$\langle f\rangle$
act on
![]() $S_k$
. For
$S_k$
. For
![]() $\{ i_1,\ldots,i_k \}\in S_k$
, let
$\{ i_1,\ldots,i_k \}\in S_k$
, let
![]() $O_{\{ i_1,\ldots,i_k \}}$
denote the orbit of
$O_{\{ i_1,\ldots,i_k \}}$
denote the orbit of
![]() $\{ i_1,\ldots,i_k \}$
under group action,
$\{ i_1,\ldots,i_k \}$
under group action,
The theory of group action tells us that
![]() $S_k$
can be divided to disjoint orbits with equal size p. In addition, for any
$S_k$
can be divided to disjoint orbits with equal size p. In addition, for any
![]() $\{ i_1,\ldots,i_k \}\in S_k$
, when s varies from 0 to
$\{ i_1,\ldots,i_k \}\in S_k$
, when s varies from 0 to
![]() $p-1$
,
$p-1$
,
![]() $\sum_{j=1}^k i^s_j \,(\textrm{mod}\,p)$
takes all values in
$\sum_{j=1}^k i^s_j \,(\textrm{mod}\,p)$
takes all values in
![]() $\{0,\ldots, p-1\}$
.
$\{0,\ldots, p-1\}$
.
If the claim above were not true, then there would exist
![]() $0\le s_1<s_2 \le p-1$
such that
$0\le s_1<s_2 \le p-1$
such that
 \begin{equation*} \sum_{j=1}^k i^{s_1}_j = \sum_{j=1}^k i^{s_2}_j \,(\textrm{mod}\,p) \quad \Rightarrow \quad \sum_{j=1}^k(i_j+s_1) = \sum_{j=1}^k (i_j+s_2) \,(\textrm{mod}\,p). \end{equation*}
\begin{equation*} \sum_{j=1}^k i^{s_1}_j = \sum_{j=1}^k i^{s_2}_j \,(\textrm{mod}\,p) \quad \Rightarrow \quad \sum_{j=1}^k(i_j+s_1) = \sum_{j=1}^k (i_j+s_2) \,(\textrm{mod}\,p). \end{equation*}
The equality above shows that
![]() $p\mid k(s_2-s_1)$
, which implies
$p\mid k(s_2-s_1)$
, which implies
![]() $p\mid k$
or
$p\mid k$
or
![]() $p\mid(s_2-s_1)$
, leading to a contradiction since
$p\mid(s_2-s_1)$
, leading to a contradiction since
![]() $1\le k,s_2-s_1\le p-1$
.
$1\le k,s_2-s_1\le p-1$
.
The argument above shows that
![]() $S_k$
is a union of disjoint orbits of equal size p. And in each orbit, for
$S_k$
is a union of disjoint orbits of equal size p. And in each orbit, for
![]() $0\le m\le p-1$
, there exists one and only one element belonging to
$0\le m\le p-1$
, there exists one and only one element belonging to
![]() $S^m_k$
, which means the
$S^m_k$
, which means the
![]() $\{ S_k^m \;:\; 0\le m\le p-1 \}$
partition
$\{ S_k^m \;:\; 0\le m\le p-1 \}$
partition
![]() $S_k$
into p subsets with equal size, and the proof is complete.
$S_k$
into p subsets with equal size, and the proof is complete.
Figure 1 presents a special case to show the idea of the proof, with
![]() $p=7$
and
$p=7$
and
![]() $k=3$
; the proof proceeds as shown.
$k=3$
; the proof proceeds as shown.

Figure 1. An example of the method in the proof.
Next, we prove the main theorem on algorithm
![]() $\mathcal{A}_2(p)$
.
$\mathcal{A}_2(p)$
.
Theorem 1.
Let X denote a biased coin with probability
![]() $a \in (0, 1)$
of getting a head, and probability
$a \in (0, 1)$
of getting a head, and probability
![]() $b = 1 - a$
of getting a tail. For a prime p,
$b = 1 - a$
of getting a tail. For a prime p,
![]() $\mathcal{A}_2(p)$
has the following properties:
$\mathcal{A}_2(p)$
has the following properties:
-
(i)
 $\mathcal{A}_2(p)$
terminates in a finite number of flips with probability 1. The algorithm returns a uniform distribution on
$\mathcal{A}_2(p)$
terminates in a finite number of flips with probability 1. The algorithm returns a uniform distribution on
 $\{0,\ldots,p-1\}\;:\;$
$\{0,\ldots,p-1\}\;:\;$
 $\mathbb{P}(\mathcal{A}_2(p)=m) = {1}/{p}$
for all
$\mathbb{P}(\mathcal{A}_2(p)=m) = {1}/{p}$
for all
 $0\le m\le p-1$
.
$0\le m\le p-1$
. -
(ii) The expected number of flips terminating
 $\mathcal{A}_2(p)$
is
$\mathcal{A}_2(p)$
is
 ${p}/({1-a^{p}-b^{p}})$
, which means that when p is large, the average running time approximates to the linear
${p}/({1-a^{p}-b^{p}})$
, which means that when p is large, the average running time approximates to the linear
 $\operatorname{O}\!(p)$
.
$\operatorname{O}\!(p)$
. -
(iii) By letting
 $p=2$
,
$p=2$
,
 $\mathcal{A}_2(2)$
is exactly Von Neumann’s algorithm
$\mathcal{A}_2(2)$
is exactly Von Neumann’s algorithm
 $\mathcal{A}_1$
.
$\mathcal{A}_1$
.
Proof. Let
![]() ${\boldsymbol{{X}}}^{p}=(X_0, \ldots, X_{p-1})$
be the outcome of p flips of a biased coin, a random variable taking values in
${\boldsymbol{{X}}}^{p}=(X_0, \ldots, X_{p-1})$
be the outcome of p flips of a biased coin, a random variable taking values in
![]() $\{H,T\}^{p}$
. Based on the correspondences in (3) and (4), and the definition of
$\{H,T\}^{p}$
. Based on the correspondences in (3) and (4), and the definition of
![]() $S^m_k$
in (8), each
$S^m_k$
in (8), each
![]() ${\boldsymbol{{x}}}^p \in \{H,T\}^{p}$
corresponds to one and only one element in
${\boldsymbol{{x}}}^p \in \{H,T\}^{p}$
corresponds to one and only one element in
![]() $S^m_k$
by
$S^m_k$
by
![]() $N_{\text{head}}({\boldsymbol{{x}}}^p)=k$
and
$N_{\text{head}}({\boldsymbol{{x}}}^p)=k$
and
![]() $S_{\text{head}}({\boldsymbol{{x}}}^p)=m\,(\textrm{mod}\,p)$
for some k and m, where
$S_{\text{head}}({\boldsymbol{{x}}}^p)=m\,(\textrm{mod}\,p)$
for some k and m, where
![]() $N_{\text{head}}({\boldsymbol{{x}}}^p)$
and
$N_{\text{head}}({\boldsymbol{{x}}}^p)$
and
![]() $S_{\text{head}}({\boldsymbol{{x}}}^p)$
in (1) are the count and rank sum of heads respectively. Recall the definition of
$S_{\text{head}}({\boldsymbol{{x}}}^p)$
in (1) are the count and rank sum of heads respectively. Recall the definition of
![]() $S_k$
in (2); then, by Lemma 1, the
$S_k$
in (2); then, by Lemma 1, the
![]() $\{ S_k^m \;:\; 0\le m\le p-1 \}$
partition
$\{ S_k^m \;:\; 0\le m\le p-1 \}$
partition
![]() $S_k$
into p subsets with equal size.
$S_k$
into p subsets with equal size.
Let
![]() $\{{\boldsymbol{{Y}}}_i = (X_{ip}, \ldots, X_{ip+p-1})\;:\; i\ge 0\}$
be i.i.d. outcomes of p flips, and
$\{{\boldsymbol{{Y}}}_i = (X_{ip}, \ldots, X_{ip+p-1})\;:\; i\ge 0\}$
be i.i.d. outcomes of p flips, and
![]() $\tau$
be the first time
$\tau$
be the first time
![]() ${\boldsymbol{{Y}}}_i$
is neither all heads nor all tails. Then, for
${\boldsymbol{{Y}}}_i$
is neither all heads nor all tails. Then, for
![]() $0 \le m \le p-1$
, we have
$0 \le m \le p-1$
, we have
 \begin{align*} \mathbb{P}(\mathcal{A}_2(p)=m) & = \mathbb{P}(S_{\text{head}}({\boldsymbol{{Y}}}_\tau) = m \,(\textrm{mod}\,p)) \\[5pt] & = \mathbb{P}(S_{\text{head}}({\boldsymbol{{X}}}^{p}) = m \,(\textrm{mod}\,p) \mid {\boldsymbol{{X}}}^{p}\text{ is neither all heads nor all tails}) \\[5pt] & = \frac{\mathbb{P}(S_{\text{head}}({\boldsymbol{{X}}}^{p})=m \,(\textrm{mod}\,p), N_{\text{head}}({\boldsymbol{{X}}}^{p}) =k \text{ for some } 1\le k\le p-1)}{\mathbb{P}(N_{\text{head}}({\boldsymbol{{X}}}^{p}) =k \text{ for some } 1\le k\le p-1)} \\[5pt] & = \frac{\sum_{k=1}^{p-1}\mathbb{P}(S_{\text{head}}({\boldsymbol{{X}}}^{p})=m \,(\textrm{mod}\,p), N_{\text{head}}({\boldsymbol{{X}}}^{p}) =k)}{\sum_{k=1}^{p-1}\mathbb{P}( N_{\text{head}}({\boldsymbol{{X}}}^{p}) =k )} \\[5pt] & = \frac{\sum_{k=1}^{p-1}|S_k^m|a^k b^{p-k}}{\sum_{k=1}^{p-1}|S_k|a^k b^{p-k}} = \frac{1}{p}, \end{align*}
\begin{align*} \mathbb{P}(\mathcal{A}_2(p)=m) & = \mathbb{P}(S_{\text{head}}({\boldsymbol{{Y}}}_\tau) = m \,(\textrm{mod}\,p)) \\[5pt] & = \mathbb{P}(S_{\text{head}}({\boldsymbol{{X}}}^{p}) = m \,(\textrm{mod}\,p) \mid {\boldsymbol{{X}}}^{p}\text{ is neither all heads nor all tails}) \\[5pt] & = \frac{\mathbb{P}(S_{\text{head}}({\boldsymbol{{X}}}^{p})=m \,(\textrm{mod}\,p), N_{\text{head}}({\boldsymbol{{X}}}^{p}) =k \text{ for some } 1\le k\le p-1)}{\mathbb{P}(N_{\text{head}}({\boldsymbol{{X}}}^{p}) =k \text{ for some } 1\le k\le p-1)} \\[5pt] & = \frac{\sum_{k=1}^{p-1}\mathbb{P}(S_{\text{head}}({\boldsymbol{{X}}}^{p})=m \,(\textrm{mod}\,p), N_{\text{head}}({\boldsymbol{{X}}}^{p}) =k)}{\sum_{k=1}^{p-1}\mathbb{P}( N_{\text{head}}({\boldsymbol{{X}}}^{p}) =k )} \\[5pt] & = \frac{\sum_{k=1}^{p-1}|S_k^m|a^k b^{p-k}}{\sum_{k=1}^{p-1}|S_k|a^k b^{p-k}} = \frac{1}{p}, \end{align*}
where the last identity is implied by the fact that
![]() $|S^m_k| = \frac{1}{p}\binom{p}{k}=\frac{1}{p}|S_k|$
.
$|S^m_k| = \frac{1}{p}\binom{p}{k}=\frac{1}{p}|S_k|$
.
Let E denote the expected number of flips terminating
![]() $\mathcal{A}_2(p)$
. Hence, E satisfies
$\mathcal{A}_2(p)$
. Hence, E satisfies
from which we have
We have also come up with a creative and short proof for Theorem 1(i) using random variables in the residue class
![]() $\mathbb{Z}_{p}$
; see Appendix A.
$\mathbb{Z}_{p}$
; see Appendix A.
5. Generating a uniform distribution on n elements
Let n be any positive integer with prime factorization
![]() $n=\prod_{i=1}^s p_i^{t_i}$
. Let
$n=\prod_{i=1}^s p_i^{t_i}$
. Let
![]() $\mathcal{M}$
be the set of all prime factors of n considering multiplicity, which means
$\mathcal{M}$
be the set of all prime factors of n considering multiplicity, which means
![]() $p_i$
appears
$p_i$
appears
![]() $t_i$
times in
$t_i$
times in
![]() $\mathcal{M}$
. The algorithm
$\mathcal{M}$
. The algorithm
![]() $\mathcal{A}_3(n)$
shown in Algorithm 4 generates a discrete uniform distribution on the set
$\mathcal{A}_3(n)$
shown in Algorithm 4 generates a discrete uniform distribution on the set
![]() $\{0,\ldots, n\!-\!1\}$
in an iterative way.
$\{0,\ldots, n\!-\!1\}$
in an iterative way.
Algorithm 4
![]() $\mathcal{A}_3(n)$
: Generating a discrete uniform distribution on the set
$\mathcal{A}_3(n)$
: Generating a discrete uniform distribution on the set
![]() $\{0,\ldots,n\!-\!1\}$
.
$\{0,\ldots,n\!-\!1\}$
.

The following theorem shows the validity of algorithm
![]() $\mathcal{A}_3(n)$
.
$\mathcal{A}_3(n)$
.
Theorem 2.
For any integer n,
![]() $\mathcal{A}_3(n)$
has the following properties:
$\mathcal{A}_3(n)$
has the following properties:
-
(i)
 $\mathcal{A}_3(n)$
terminates in a finite number of flips with probability 1. It returns a uniform distribution on
$\mathcal{A}_3(n)$
terminates in a finite number of flips with probability 1. It returns a uniform distribution on
 $\{0, \ldots, n\!-\!1\}\;:\;$
$\{0, \ldots, n\!-\!1\}\;:\;$
 $\mathbb{P}(\mathcal{A}_3(n)=m)={1}/{n}$
for all
$\mathbb{P}(\mathcal{A}_3(n)=m)={1}/{n}$
for all
 $0\le m\le n\!-\!1$
.
$0\le m\le n\!-\!1$
. -
(ii) When n has prime factorization
 $\prod_{i=1}^s p_i^{t_i}$
, the expected number of flips terminating
$\prod_{i=1}^s p_i^{t_i}$
, the expected number of flips terminating
 $\mathcal{A}_3(n)$
isTherefore, the average running time is approximately
$\mathcal{A}_3(n)$
isTherefore, the average running time is approximately \begin{equation*} \sum_{i=1}^s \frac{t_i p_i}{1-a^{p_i} - b^{p_i}}. \end{equation*}
\begin{equation*} \sum_{i=1}^s \frac{t_i p_i}{1-a^{p_i} - b^{p_i}}. \end{equation*}
 $\sum_{i=1}^s t_i p_i$
for large n.
$\sum_{i=1}^s t_i p_i$
for large n.
-
(iii) The overall order of the average running time is
 $\operatorname{O}\!(n/\log\!(n))$
.
$\operatorname{O}\!(n/\log\!(n))$
.
Proof. To show (i), note that each outcome of
![]() $\mathcal{A}_3(n)$
corresponds to one and only one sequence of outcomes of
$\mathcal{A}_3(n)$
corresponds to one and only one sequence of outcomes of
![]() $\mathcal{A}_2(p_i)$
. For this fact, first we consider a simplified case where
$\mathcal{A}_2(p_i)$
. For this fact, first we consider a simplified case where
![]() $n=p_1p_2$
is a product of two prime numbers
$n=p_1p_2$
is a product of two prime numbers
![]() $p_1$
and
$p_1$
and
![]() $p_2$
, and
$p_2$
, and
![]() $p_1$
may equal
$p_1$
may equal
![]() $p_2$
.
$p_2$
.
Given
![]() $n=p_1 p_2$
, then
$n=p_1 p_2$
, then
![]() $\mathcal{M} = \{p_1, p_2 \}$
. Suppose we first get
$\mathcal{M} = \{p_1, p_2 \}$
. Suppose we first get
![]() $p_1$
from
$p_1$
from
![]() $\mathcal{M}$
and then
$\mathcal{M}$
and then
![]() $p_2$
. Then the outcomes
$p_2$
. Then the outcomes
![]() $\mathcal{A}_2(p_1)=m_1$
and
$\mathcal{A}_2(p_1)=m_1$
and
![]() $\mathcal{A}_2(p_2)=m_2$
correspond to the outcome
$\mathcal{A}_2(p_2)=m_2$
correspond to the outcome
![]() $\mathcal{A}_3(n)=m_1 p_2 + m_2$
. Since
$\mathcal{A}_3(n)=m_1 p_2 + m_2$
. Since
![]() $0\le m_1\le p_1-1$
and
$0\le m_1\le p_1-1$
and
![]() $0\le m_2\le p_2-1$
, we have the range for
$0\le m_2\le p_2-1$
, we have the range for
![]() $\mathcal{A}_3(n)$
:
$\mathcal{A}_3(n)$
:
which shows that
![]() $\mathcal{A}_3(n)\in \{0, \ldots, n\!-\!1\}$
. Note that, for
$\mathcal{A}_3(n)\in \{0, \ldots, n\!-\!1\}$
. Note that, for
![]() $0\le m\le n\!-\!1$
, there exists one and only one pair of
$0\le m\le n\!-\!1$
, there exists one and only one pair of
![]() $(m_1, m_2)$
as
$(m_1, m_2)$
as
satisfying the equation
![]() $m = m_1p_2+m_2$
$m = m_1p_2+m_2$
![]() $(0\le m_1\le p_1-1, \, 0\le m_2\le p_2-1)$
. So, the outcome
$(0\le m_1\le p_1-1, \, 0\le m_2\le p_2-1)$
. So, the outcome
![]() $\mathcal{A}_3(n) = m$
corresponds to the outcomes
$\mathcal{A}_3(n) = m$
corresponds to the outcomes
![]() $\mathcal{A}_2(p_1)=m_1$
and
$\mathcal{A}_2(p_1)=m_1$
and
![]() $\mathcal{A}_2(p_2)=m_2$
.
$\mathcal{A}_2(p_2)=m_2$
.
For the general case
![]() $n=\prod_{i=1}^s p_i^{t_i}$
, based on the same method as above, we conclude that, for each m, there exists a unique set
$n=\prod_{i=1}^s p_i^{t_i}$
, based on the same method as above, we conclude that, for each m, there exists a unique set
![]() $\{ m_{p^\prime}\;:\; p^\prime\in \mathcal{M}\}$
such that the outcome
$\{ m_{p^\prime}\;:\; p^\prime\in \mathcal{M}\}$
such that the outcome
![]() $\mathcal{A}_3(n) = m$
corresponds to the outcomes
$\mathcal{A}_3(n) = m$
corresponds to the outcomes
![]() $\mathcal{A}_2(p^\prime)=m_{p^\prime}$
$\mathcal{A}_2(p^\prime)=m_{p^\prime}$
![]() $(p^\prime \in \mathcal{M})$
. Therefore, the probability of
$(p^\prime \in \mathcal{M})$
. Therefore, the probability of
![]() $\mathcal{A}_3(n)=m$
is
$\mathcal{A}_3(n)=m$
is
 \begin{equation*} \mathbb{P}(\mathcal{A}_3(n)=m) = \prod_{p^\prime\in\mathcal{M}}\mathbb{P}(\mathcal{A}_2(p^\prime)=m_{p^\prime}) = \prod_{i=1}^s \bigg(\frac{1}{p_i}\bigg)^{t_i} = \frac{1}{n} \quad \text{for all } 0\le m\le n\!-\!1. \end{equation*}
\begin{equation*} \mathbb{P}(\mathcal{A}_3(n)=m) = \prod_{p^\prime\in\mathcal{M}}\mathbb{P}(\mathcal{A}_2(p^\prime)=m_{p^\prime}) = \prod_{i=1}^s \bigg(\frac{1}{p_i}\bigg)^{t_i} = \frac{1}{n} \quad \text{for all } 0\le m\le n\!-\!1. \end{equation*}
To prove (ii), note that, for
![]() $n=\prod_{i=1}^s p_i^{t_i}$
, the set
$n=\prod_{i=1}^s p_i^{t_i}$
, the set
![]() $\mathcal{M}$
contains each prime factor
$\mathcal{M}$
contains each prime factor
![]() $p_i$
$p_i$
![]() $t_i$
times. By the iterative construction of
$t_i$
times. By the iterative construction of
![]() $\mathcal{A}_3(n)$
, we need to run
$\mathcal{A}_3(n)$
, we need to run
![]() $\mathcal{A}_3(p_i)$
once every time we pick
$\mathcal{A}_3(p_i)$
once every time we pick
![]() $p_i$
from
$p_i$
from
![]() $\mathcal{M}$
. Based on Theorem 1(ii), the expected number of flips for
$\mathcal{M}$
. Based on Theorem 1(ii), the expected number of flips for
![]() $\mathcal{A}_2(p_i)$
is
$\mathcal{A}_2(p_i)$
is
![]() ${p_i}/({1 - a^{p_i} - b^{p_i}})$
, from which we conclude that the expected number of flips terminating
${p_i}/({1 - a^{p_i} - b^{p_i}})$
, from which we conclude that the expected number of flips terminating
![]() $\mathcal{A}_3(n)$
is
$\mathcal{A}_3(n)$
is
To analyze the average running time of the algorithm
![]() $\mathcal{A}_3(n)$
, define the function
$\mathcal{A}_3(n)$
, define the function
![]() $c(n)=\sum_{i=1}^s t_i p_i$
to be the sum of prime factors of n multiplied by their multiplicity, which is a good approximation to the average running time of
$c(n)=\sum_{i=1}^s t_i p_i$
to be the sum of prime factors of n multiplied by their multiplicity, which is a good approximation to the average running time of
![]() $\mathcal{A}_3(n)$
according to Theorem 2(ii). We see that, for prime numbers, the complexity is linear. For composite numbers, the complexity is sublinear. For
$\mathcal{A}_3(n)$
according to Theorem 2(ii). We see that, for prime numbers, the complexity is linear. For composite numbers, the complexity is sublinear. For
![]() $n=p_1^{t_1}$
, since
$n=p_1^{t_1}$
, since
![]() $c(n)=t_1 p_1$
, the average running time is almost
$c(n)=t_1 p_1$
, the average running time is almost
![]() $\log\!(n)$
. We have the following theorem from number theory [Reference Jakimczuk4, Corollary 2.11]:
$\log\!(n)$
. We have the following theorem from number theory [Reference Jakimczuk4, Corollary 2.11]:
So, we have an overall sublinear
![]() $\operatorname{O}\!(n/\log\!(n))$
complexity for the algorithm
$\operatorname{O}\!(n/\log\!(n))$
complexity for the algorithm
![]() $\mathcal{A}_3(n)$
.
$\mathcal{A}_3(n)$
.
Remark 1. In [Reference Elias2], another method for generating a discrete uniform distribution on the set
![]() $\{0,\ldots ,n - 1\}$
was proposed. Elias’ method needs Elias’ function mapping outcomes of the random source to target values. However, unlike Theorem 2(iii), the efficiency of Elias’ method is defined by complicated mathematical formulas without analytic and concise form, and is thus hard to analyze theoretically. Besides, Elias’ method suffers the same problem as Dijkstra’s method mentioned in Section 3. The computation of Elias’ function, an essential preprocessing step of Elias’ method, is computationally inefficient, and the storage of Elias’ function is also an excessive space cost.
$\{0,\ldots ,n - 1\}$
was proposed. Elias’ method needs Elias’ function mapping outcomes of the random source to target values. However, unlike Theorem 2(iii), the efficiency of Elias’ method is defined by complicated mathematical formulas without analytic and concise form, and is thus hard to analyze theoretically. Besides, Elias’ method suffers the same problem as Dijkstra’s method mentioned in Section 3. The computation of Elias’ function, an essential preprocessing step of Elias’ method, is computationally inefficient, and the storage of Elias’ function is also an excessive space cost.
Appendix A. A new proof for Theorem 1(i)
Consider random variables taking values in
![]() $\mathbb{Z}_p=\{ \bar{0}, \ldots, \overline{p-1} \}$
, where
$\mathbb{Z}_p=\{ \bar{0}, \ldots, \overline{p-1} \}$
, where
![]() $\overline{i}$
represents the residual class of i modulo p. Regard
$\overline{i}$
represents the residual class of i modulo p. Regard
![]() $\bar{0}$
as a tail and
$\bar{0}$
as a tail and
![]() $\bar{1}$
as a head. Let X denote the outcome of a flip satisfying
$\bar{1}$
as a head. Let X denote the outcome of a flip satisfying
![]() $\mathbb{P}(X=\overline{0})=a$
and
$\mathbb{P}(X=\overline{0})=a$
and
![]() $\mathbb{P}(X=\overline{1})=b$
. Let
$\mathbb{P}(X=\overline{1})=b$
. Let
![]() $X_0, \ldots, X_{p-1}$
be independent copies of X. Define
$X_0, \ldots, X_{p-1}$
be independent copies of X. Define
![]() ${\boldsymbol{{X}}}^{p}=(X_0,\ldots, X_{p-1})$
to be the outcome of p flips. We then have the following equivalences:
${\boldsymbol{{X}}}^{p}=(X_0,\ldots, X_{p-1})$
to be the outcome of p flips. We then have the following equivalences:
 \begin{align*} {\boldsymbol{{X}}}^{p}\text{ is all heads or all tails} & \Longleftrightarrow X_i=\bar{0} \text{ for all } 0\le i\le p-1 \\[5pt] & \quad\, \text{or } X_i=\bar{1} \text{ for all } 0\le i\le p-1 \\[5pt] & \Longleftrightarrow \sum_{i=0}^{p-1}X_i=\bar{0}, \\[5pt] S_{\text{head}}({\boldsymbol{{X}}}^{p}) = m(\textrm{mod}\,p) & \Longleftrightarrow \sum_{i=0}^{p-1}\overline{i}\cdot X_i = \overline{m}.\end{align*}
\begin{align*} {\boldsymbol{{X}}}^{p}\text{ is all heads or all tails} & \Longleftrightarrow X_i=\bar{0} \text{ for all } 0\le i\le p-1 \\[5pt] & \quad\, \text{or } X_i=\bar{1} \text{ for all } 0\le i\le p-1 \\[5pt] & \Longleftrightarrow \sum_{i=0}^{p-1}X_i=\bar{0}, \\[5pt] S_{\text{head}}({\boldsymbol{{X}}}^{p}) = m(\textrm{mod}\,p) & \Longleftrightarrow \sum_{i=0}^{p-1}\overline{i}\cdot X_i = \overline{m}.\end{align*}
Also note that, for any permutation
![]() $\sigma$
, we have
$\sigma$
, we have
![]() $(X_0,\ldots, X_{p-1}) \overset{\textrm{d}}{=} (X_{\sigma(0)},\ldots, X_{\sigma(p-1)})$
, since all the
$(X_0,\ldots, X_{p-1}) \overset{\textrm{d}}{=} (X_{\sigma(0)},\ldots, X_{\sigma(p-1)})$
, since all the
![]() $X_i$
are i.i.d. In the following, we let
$X_i$
are i.i.d. In the following, we let
![]() $\sigma$
denote the special permutation
$\sigma$
denote the special permutation
 \begin{equation*} \sigma = \left( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 0 & 1 & \cdots & p-2 & p-1 \\[5pt] 1 & 2 & \cdots & p-1 & 0 \end{array} \right).\end{equation*}
\begin{equation*} \sigma = \left( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 0 & 1 & \cdots & p-2 & p-1 \\[5pt] 1 & 2 & \cdots & p-1 & 0 \end{array} \right).\end{equation*}
For fixed
![]() $t\neq \bar{0}\in \mathbb{Z}_{p}$
, we have
$t\neq \bar{0}\in \mathbb{Z}_{p}$
, we have
 \begin{align*} \mathbb{P}\Bigg(\sum_{i=0}^{p-1}\overline{i}\cdot X_i=\bar{0} ,\ \sum_{i=0}^{p-1}X_i=t\Bigg) & = \mathbb{P}\Bigg(\sum_{i=0}^{p-1}\overline{i}\cdot X_i + \sum_{i=0}^{p-1}X_i=t ,\ \sum_{i=0}^{p-1}X_i=t\Bigg) \\[5pt] & = \mathbb{P}\Bigg(\sum_{i=0}^{p-1}\overline{i+1}\cdot X_i=t ,\ \sum_{i=0}^{p-1}X_i=t\Bigg) \\[5pt] & = \mathbb{P}\Bigg(\sum_{i=0}^{p-1}\overline{i+1}\cdot X_{\sigma(i)}=t ,\ \sum_{i=0}^{p-1}X_{\sigma(i)}=t\Bigg) \\[5pt] & = \mathbb{P}\left(\sum_{i=0}^{p-1}\overline{i}\cdot X_i=t ,\ \sum_{i=0}^{p-1}X_i=t\right).\end{align*}
\begin{align*} \mathbb{P}\Bigg(\sum_{i=0}^{p-1}\overline{i}\cdot X_i=\bar{0} ,\ \sum_{i=0}^{p-1}X_i=t\Bigg) & = \mathbb{P}\Bigg(\sum_{i=0}^{p-1}\overline{i}\cdot X_i + \sum_{i=0}^{p-1}X_i=t ,\ \sum_{i=0}^{p-1}X_i=t\Bigg) \\[5pt] & = \mathbb{P}\Bigg(\sum_{i=0}^{p-1}\overline{i+1}\cdot X_i=t ,\ \sum_{i=0}^{p-1}X_i=t\Bigg) \\[5pt] & = \mathbb{P}\Bigg(\sum_{i=0}^{p-1}\overline{i+1}\cdot X_{\sigma(i)}=t ,\ \sum_{i=0}^{p-1}X_{\sigma(i)}=t\Bigg) \\[5pt] & = \mathbb{P}\left(\sum_{i=0}^{p-1}\overline{i}\cdot X_i=t ,\ \sum_{i=0}^{p-1}X_i=t\right).\end{align*}
Note that any
![]() $t\neq \bar{0}$
can generate
$t\neq \bar{0}$
can generate
![]() $\mathbb{Z}_{p}$
. By iterating the derivation above, we have
$\mathbb{Z}_{p}$
. By iterating the derivation above, we have
 \begin{align*} \mathbb{P}\Bigg(\sum_{i=0}^{p-1}\overline{i}\cdot X_i=k ,\ \sum_{i=0}^{p-1}X_i= t \Bigg) =\mathbb{P}\Bigg(\sum_{i=0}^{p-1}\overline{i}\cdot X_i=s ,\ \sum_{i=0}^{p-1}X_i= t \Bigg) \text{ for all } k,s \in \mathbb{Z}_{p}.\end{align*}
\begin{align*} \mathbb{P}\Bigg(\sum_{i=0}^{p-1}\overline{i}\cdot X_i=k ,\ \sum_{i=0}^{p-1}X_i= t \Bigg) =\mathbb{P}\Bigg(\sum_{i=0}^{p-1}\overline{i}\cdot X_i=s ,\ \sum_{i=0}^{p-1}X_i= t \Bigg) \text{ for all } k,s \in \mathbb{Z}_{p}.\end{align*}
Summing over
![]() $t \neq \bar{0}$
on both sides of the above equation, we have, for
$t \neq \bar{0}$
on both sides of the above equation, we have, for
![]() $k,s\in \mathbb{Z}_{p}$
,
$k,s\in \mathbb{Z}_{p}$
,
 \begin{align*}\mathbb{P}\left(\sum_{i=0}^{p-1}\overline{i}\cdot X_i=k ,\quad \sum_{i=0}^{p-1}X_i\neq \bar{0}\right)
& = \sum_{t\neq \bar{0}}\mathbb{P}\left(\sum_{i=0}^{p-1}\overline{i}\cdot X_i=k ,\quad \sum_{i=0}^{p-1}X_i=t\right) \\
& = \sum_{t\neq \bar{0}}\mathbb{P}\left(\sum_{i=0}^{p-1}\overline{i}\cdot X_i=s ,\quad \sum_{i=0}^{p-1}X_i=t\right) \\
& = \mathbb{P}\left(\sum_{i=0}^{p-1}\overline{i}\cdot X_i=s ,\quad \sum_{i=0}^{p-1}X_i\neq \bar{0}\right),\end{align*}
\begin{align*}\mathbb{P}\left(\sum_{i=0}^{p-1}\overline{i}\cdot X_i=k ,\quad \sum_{i=0}^{p-1}X_i\neq \bar{0}\right)
& = \sum_{t\neq \bar{0}}\mathbb{P}\left(\sum_{i=0}^{p-1}\overline{i}\cdot X_i=k ,\quad \sum_{i=0}^{p-1}X_i=t\right) \\
& = \sum_{t\neq \bar{0}}\mathbb{P}\left(\sum_{i=0}^{p-1}\overline{i}\cdot X_i=s ,\quad \sum_{i=0}^{p-1}X_i=t\right) \\
& = \mathbb{P}\left(\sum_{i=0}^{p-1}\overline{i}\cdot X_i=s ,\quad \sum_{i=0}^{p-1}X_i\neq \bar{0}\right),\end{align*}
which implies, for
![]() $k,s\in \mathbb{Z}_{p}$
,
$k,s\in \mathbb{Z}_{p}$
,
 \begin{equation*} \mathbb{P}\Bigg(\sum_{i=0}^{p-1}\overline{i}\cdot X_i=k \,\Big|\, \sum_{i=0}^{p-1}X_i\neq \bar{0}\Bigg) = \mathbb{P}\Bigg(\sum_{i=0}^{p-1}\overline{i}\cdot X_i=s \,\Big|\, \sum_{i=0}^{p-1}X_i\neq \bar{0}\Bigg).\end{equation*}
\begin{equation*} \mathbb{P}\Bigg(\sum_{i=0}^{p-1}\overline{i}\cdot X_i=k \,\Big|\, \sum_{i=0}^{p-1}X_i\neq \bar{0}\Bigg) = \mathbb{P}\Bigg(\sum_{i=0}^{p-1}\overline{i}\cdot X_i=s \,\Big|\, \sum_{i=0}^{p-1}X_i\neq \bar{0}\Bigg).\end{equation*}
This equality is equivalent to the statement
 \begin{align*}\mathbb{P}({S_{{\text{head}}}}({{\mathbf{X}}^p}) = k({\text{mod}}{\mkern 1mu} p)\mid {{\mathbf{X}}^p}{\text{ is neither all heads nor all tails}}) \\ &\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!= \mathbb{P}({S_{{\text{head}}}}({{\mathbf{X}}^p}) = s({\text{mod}}{\mkern 1mu} p)\mid {{\mathbf{X}}^p}{\text{ is neither all heads nor all tails}}) \\\end{align*}
\begin{align*}\mathbb{P}({S_{{\text{head}}}}({{\mathbf{X}}^p}) = k({\text{mod}}{\mkern 1mu} p)\mid {{\mathbf{X}}^p}{\text{ is neither all heads nor all tails}}) \\ &\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!= \mathbb{P}({S_{{\text{head}}}}({{\mathbf{X}}^p}) = s({\text{mod}}{\mkern 1mu} p)\mid {{\mathbf{X}}^p}{\text{ is neither all heads nor all tails}}) \\\end{align*}
for all
![]() $0\le k,s\le p-1$
, as desired.
$0\le k,s\le p-1$
, as desired.
Acknowledgements
The author acknowledges Prof. Mei Wang at UChicago for helpful discussions and advice, and thanks PhD candidate Haoyu Wei at UCSD for useful suggestions and kind support. The author also acknowledges the editor of Journal of Applied Probability and the two anonymous referees for their valuable comments and remarks.
Funding information
There are no funding bodies to thank relating to the creation of this article.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.