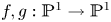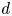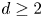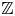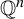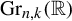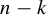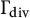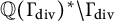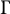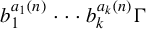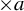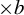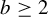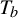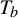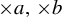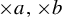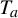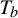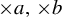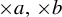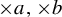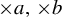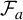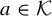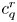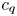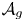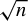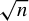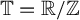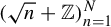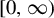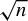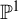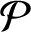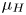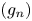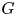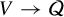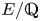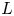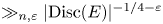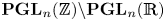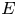33 results
Joint partial equidistribution of Farey rays in negatively curved manifolds and trees
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 08 January 2024, pp. 1-37
-
- Article
- Export citation
Dynamics on ℙ1: preperiodic points and pairwise stability
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 356-387
- Print publication:
- February 2024
-
- Article
- Export citation
Equidistribution of rational subspaces and their shapes
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 10 November 2023, pp. 1-54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A new way to tackle a conjecture of Rémond
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 31 October 2023, pp. 1-24
-
- Article
- Export citation
Pointwise convergence in nilmanifolds along smooth functions of polynomial growth
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 25 September 2023, pp. 1963-2008
- Print publication:
- July 2024
-
- Article
- Export citation
ON THE N-POINT CORRELATION OF VAN DER CORPUT SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 15 September 2023, pp. 471-475
- Print publication:
- June 2024
-
- Article
- Export citation
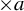 $\times a$ and
$\times a$ and 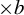 $\times b$ empirical measures, the irregular set and entropy
$\times b$ empirical measures, the irregular set and entropy
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 15 August 2023, pp. 1673-1692
- Print publication:
- June 2024
-
- Article
- Export citation
Equidistribution for matings of quadratic maps with the modular group
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 12 May 2023, pp. 859-887
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equidistribution of Hodge loci II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 12 January 2023, pp. 1-52
- Print publication:
- January 2023
-
- Article
- Export citation
Rational points on nonlinear horocycles and pigeonhole statistics for the fractional parts of
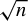 $\sqrt {n}$
$\sqrt {n}$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 08 September 2022, pp. 3108-3130
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasi-adelic measures and equidistribution on
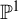 ${\mathbb P}^1$
${\mathbb P}^1$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 01 August 2022, pp. 2732-2779
- Print publication:
- August 2023
-
- Article
- Export citation
RETRACTED - THE KRONECKER–WEYL EQUIDISTRIBUTION THEOREM AND GEODESICS IN 3-MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 21 March 2022, pp. 1-44
-
- Article
- Export citation
Translates of homogeneous measures associated with observable subgroups on some homogeneous spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 22 December 2021, pp. 2657-2698
- Print publication:
- December 2021
-
- Article
- Export citation
Typical properties of periodic Teichmüller geodesics: Lyapunov exponents
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 17 November 2021, pp. 556-584
- Print publication:
- February 2023
-
- Article
- Export citation
Excursions to the cusps for geometrically finite hyperbolic orbifolds and equidistribution of closed geodesics in regular covers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 12 / December 2022
- Published online by Cambridge University Press:
- 15 November 2021, pp. 3745-3791
- Print publication:
- December 2022
-
- Article
- Export citation
Exponential mixing of frame flows for convex cocompact hyperbolic manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 08 November 2021, pp. 2585-2634
- Print publication:
- December 2021
-
- Article
- Export citation
Equidistribution of horospheres in non-positive curvature
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 28 October 2021, pp. 460-479
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-vanishing of class group L-functions for number fields with a small regulator
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 17 December 2020, pp. 2423-2436
- Print publication:
- November 2020
-
- Article
- Export citation
Primitive rational points on expanding horocycles in products of the modular surface with the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 04 June 2020, pp. 1706-1750
- Print publication:
- June 2021
-
- Article
- Export citation
Cotangent Sums Related to the Riemann Hypothesis for Various Shifts of the Argument
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 15 October 2019, pp. 522-535
- Print publication:
- September 2020
-
- Article
-
- You have access
- Open access
- Export citation