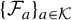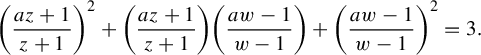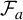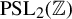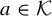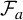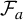1 Introduction
In 1965, Brolin [Reference Brolin3] studied asymptotic properties of polynomials
![]() $P(z)\in \mathbb {C}[z]$
of degree bigger than or equal to
$P(z)\in \mathbb {C}[z]$
of degree bigger than or equal to
![]() $2$
. He proved the existence of a probability measure for which the preimages
$2$
. He proved the existence of a probability measure for which the preimages
![]() $P^{-n}(z_0)$
at time n of any point
$P^{-n}(z_0)$
at time n of any point
![]() $z_0\in \mathbb {C}$
(with at most one exception) asymptotically equidistribute, as n tends to infinity. In 1983, Freire, Lopes, and Mañé [Reference Freire, Lopes and Mañé20] and Ljubich [Reference Ljubich24] independently proved the generalization to rational maps of degree at least
$z_0\in \mathbb {C}$
(with at most one exception) asymptotically equidistribute, as n tends to infinity. In 1983, Freire, Lopes, and Mañé [Reference Freire, Lopes and Mañé20] and Ljubich [Reference Ljubich24] independently proved the generalization to rational maps of degree at least
![]() $2$
on the Riemann sphere. These results have been generalized to different settings. For instance, see [Reference Dinh, Sibony, Gentili, Guenot and Patrizio18, §1.4] and the references therein for higher dimensions, and [Reference Favre and Rivera-Letelier19, Reference Gignac22] for the non-Archimedian setting.
$2$
on the Riemann sphere. These results have been generalized to different settings. For instance, see [Reference Dinh, Sibony, Gentili, Guenot and Patrizio18, §1.4] and the references therein for higher dimensions, and [Reference Favre and Rivera-Letelier19, Reference Gignac22] for the non-Archimedian setting.
The equidistribution properties of holomorphic correspondences have also attracted considerable interest. Roughly speaking, a holomorphic correspondence on a complex manifold X is a multivalued map induced by a formal sum
![]() $\Gamma =\sum n_i\Gamma (i)$
of complex varieties
$\Gamma =\sum n_i\Gamma (i)$
of complex varieties
![]() $\Gamma (i)\subset X\times X$
of the same dimension. The multivalued map sends z to w if
$\Gamma (i)\subset X\times X$
of the same dimension. The multivalued map sends z to w if
![]() $(z,w)$
belongs to some
$(z,w)$
belongs to some
![]() $\Gamma (i)$
(see §2.1). Let
$\Gamma (i)$
(see §2.1). Let
![]() $d(F)$
denote the number of pre-images of a generic point under F. We call this number the topological degree of F, just as in the case of rational maps. We study the existence of a Borel probability measure
$d(F)$
denote the number of pre-images of a generic point under F. We call this number the topological degree of F, just as in the case of rational maps. We study the existence of a Borel probability measure
![]() $\mu $
on X that has the property that for all but at most finitely many
$\mu $
on X that has the property that for all but at most finitely many
![]() $z_0\in X$
,
$z_0\in X$
,
as
![]() $n\to \infty $
. Here,
$n\to \infty $
. Here,
![]() $(F^n)_*$
denotes the push-forward operator associated to
$(F^n)_*$
denotes the push-forward operator associated to
![]() $F^n$
. In [Reference Dinh13], Dinh studied the case of polynomial correspondences whose Lojasiewicz exponent is strictly bigger than
$F^n$
. In [Reference Dinh13], Dinh studied the case of polynomial correspondences whose Lojasiewicz exponent is strictly bigger than
![]() $1$
, in which case we always have that
$1$
, in which case we always have that
![]() $d(F^{-1})<d(F)$
. The case where
$d(F^{-1})<d(F)$
. The case where
![]() $d(F)=d(F^{-1})$
is open but some subcases are known. For instance, Clozel, Oh, and Ullmo [Reference Clozel, Oh and Ullmo9] proved equidistribution for irreducible modular correspondences, Clozel and Otal [Reference Clozel and Otal10] proved it for exterior modular correspondences, and Clozel and Ullmo [Reference Clozel and Ullmo11] for those that are self-adjoint. On the other hand, Dinh, Kaufmann, and Wu proved in [Reference Dinh, Kaufmann and Wu15] that if such F is not weakly modular, then the statement holds for both F and
$d(F)=d(F^{-1})$
is open but some subcases are known. For instance, Clozel, Oh, and Ullmo [Reference Clozel, Oh and Ullmo9] proved equidistribution for irreducible modular correspondences, Clozel and Otal [Reference Clozel and Otal10] proved it for exterior modular correspondences, and Clozel and Ullmo [Reference Clozel and Ullmo11] for those that are self-adjoint. On the other hand, Dinh, Kaufmann, and Wu proved in [Reference Dinh, Kaufmann and Wu15] that if such F is not weakly modular, then the statement holds for both F and
![]() $F^{-1}$
. Modular correspondences are weakly modular, but the reverse containment does not hold. On a different classification, Bharali and Sridharan [Reference Bharali and Sridharan1] proved equidistribution for correspondences with
$F^{-1}$
. Modular correspondences are weakly modular, but the reverse containment does not hold. On a different classification, Bharali and Sridharan [Reference Bharali and Sridharan1] proved equidistribution for correspondences with
![]() $d(F)\geq d(F^{-1})$
having a repeller in the sense of [Reference McGehee26]. We will study a
$d(F)\geq d(F^{-1})$
having a repeller in the sense of [Reference McGehee26]. We will study a
![]() $1$
-parameter family in the gap between weak-modularity and modularity, and for which the result in [Reference Bharali and Sridharan1] does not apply.
$1$
-parameter family in the gap between weak-modularity and modularity, and for which the result in [Reference Bharali and Sridharan1] does not apply.
Our object of study is the family of correspondences
![]() $\lbrace \mathcal {F}_a\rbrace _{a\in \mathcal {K}}$
on the Riemann sphere
$\lbrace \mathcal {F}_a\rbrace _{a\in \mathcal {K}}$
on the Riemann sphere
![]() $\widehat {\mathbb {C}}$
, where
$\widehat {\mathbb {C}}$
, where
![]() $\mathcal {F}_a$
is given in affine coordinates by
$\mathcal {F}_a$
is given in affine coordinates by
 $$ \begin{align} \bigg(\frac{az+1}{z+1}\bigg)^2+\bigg(\frac{az+1}{z+1}\bigg)\bigg(\frac{aw-1}{w-1}\bigg)+\bigg(\frac{aw-1}{w-1}\bigg)^2=3, \end{align} $$
$$ \begin{align} \bigg(\frac{az+1}{z+1}\bigg)^2+\bigg(\frac{az+1}{z+1}\bigg)\bigg(\frac{aw-1}{w-1}\bigg)+\bigg(\frac{aw-1}{w-1}\bigg)^2=3, \end{align} $$
and
![]() $\mathcal {K}$
is the Klein combination locus defined in §2.2. This family was studied by Bullett et al in [Reference Bullett and Lomonaco4–Reference Bullett and Penrose6, Reference Bullett and Harvey8]. In [Reference Bullett and Lomonaco4], Bullett and Lomonaco proved that there is a two sided restriction
$\mathcal {K}$
is the Klein combination locus defined in §2.2. This family was studied by Bullett et al in [Reference Bullett and Lomonaco4–Reference Bullett and Penrose6, Reference Bullett and Harvey8]. In [Reference Bullett and Lomonaco4], Bullett and Lomonaco proved that there is a two sided restriction
![]() $f_a$
of
$f_a$
of
![]() $\mathcal {F}_a$
that is hybrid equivalent to a quadratic rational map P that has a fixed point with multiplier
$\mathcal {F}_a$
that is hybrid equivalent to a quadratic rational map P that has a fixed point with multiplier
![]() $1$
. We refer the reader to [Reference Lomonaco25] for conjugacy of parabolic-like mappings. Moreover, for the parameters for which the Julia set of P is connected, we have that
$1$
. We refer the reader to [Reference Lomonaco25] for conjugacy of parabolic-like mappings. Moreover, for the parameters for which the Julia set of P is connected, we have that
![]() $\mathcal {F}_a$
is a mating between the rational map P and the modular group
$\mathcal {F}_a$
is a mating between the rational map P and the modular group
![]() $\operatorname {PSL}_2(\mathbb {Z})$
. This generalizes a previous result by Bullett and Penrose [Reference Bullett and Penrose6]. The correspondence
$\operatorname {PSL}_2(\mathbb {Z})$
. This generalizes a previous result by Bullett and Penrose [Reference Bullett and Penrose6]. The correspondence
![]() $\mathcal {F}_a$
has two homeomorphic copies of the filled Julia set
$\mathcal {F}_a$
has two homeomorphic copies of the filled Julia set
![]() $K$
of
$K$
of
![]() $P_A$
, denoted
$P_A$
, denoted
![]() $\Lambda _{a,-}$
and
$\Lambda _{a,-}$
and
![]() $\Lambda _{a,+}$
, and they satisfy that
$\Lambda _{a,+}$
, and they satisfy that
![]() $\mathcal {F}_a^{-1}(\Lambda _{a,-})=\Lambda _{a,-}$
and
$\mathcal {F}_a^{-1}(\Lambda _{a,-})=\Lambda _{a,-}$
and
![]() $\mathcal {F}_a(\Lambda _{a,+})=\Lambda _{a,+}$
. These are called the backward and forward limit set, respectively (see §3.2).
$\mathcal {F}_a(\Lambda _{a,+})=\Lambda _{a,+}$
. These are called the backward and forward limit set, respectively (see §3.2).
The following theorem states that this family does not fit the conditions for any of the equidistribution results listed above (see §1.1).
Theorem 1.1. For every
![]() $a\in \mathcal {K}$
, we have that:
$a\in \mathcal {K}$
, we have that:
-
(1)
 $\mathcal {F}_a$
is a weakly modular correspondence that is not modular; and
$\mathcal {F}_a$
is a weakly modular correspondence that is not modular; and -
(2)
 $\partial \Lambda _{a,-}$
is not a repeller for
$\partial \Lambda _{a,-}$
is not a repeller for
 $\mathcal {F}_a$
.
$\mathcal {F}_a$
.
Furthermore, we prove that
![]() $\mathcal {F}_a$
satisfies a property that is stronger than weak-modularity (see Remark 3.4).
$\mathcal {F}_a$
satisfies a property that is stronger than weak-modularity (see Remark 3.4).
The purpose of this paper is to show that equidistribution holds for the family
![]() $\lbrace \mathcal {F}_a\rbrace _{a\in \mathcal {K}}$
. Put
$\lbrace \mathcal {F}_a\rbrace _{a\in \mathcal {K}}$
. Put

We prove the following equidistribution theorem.
Theorem 1.2. Let
![]() $a\in \mathcal {K}$
. There exist two Borel probability measures
$a\in \mathcal {K}$
. There exist two Borel probability measures
![]() $\mu _+$
and
$\mu _+$
and
![]() $\mu _-$
on
$\mu _-$
on
![]() $\widehat {\mathbb {C}}$
, with
$\widehat {\mathbb {C}}$
, with
![]() $\operatorname {supp}(\mu _+)=\partial \Lambda _{a,+}$
and
$\operatorname {supp}(\mu _+)=\partial \Lambda _{a,+}$
and
![]() $\operatorname {supp}(\mu _-)=\partial \Lambda _{a,-}$
, such that for every
$\operatorname {supp}(\mu _-)=\partial \Lambda _{a,-}$
, such that for every
![]() $z_0\in \widehat {\mathbb {C}}\setminus \mathcal {E}_a$
,
$z_0\in \widehat {\mathbb {C}}\setminus \mathcal {E}_a$
,
weakly, as
![]() $n\to \infty $
.
$n\to \infty $
.
In later work [Reference Matus de la Parra12], we prove that the measures
![]() $\mu _+$
and
$\mu _+$
and
![]() $\mu _-$
maximize entropy: the metric entropy in [Reference Vivas and Sirvent31] yields equality for the half-variational principle with the topological entropy in [Reference Dinh and Sibony17].
$\mu _-$
maximize entropy: the metric entropy in [Reference Vivas and Sirvent31] yields equality for the half-variational principle with the topological entropy in [Reference Dinh and Sibony17].
Let F be a holomorphic correspondence on X with graph
![]() $\Gamma $
. Denote by
$\Gamma $
. Denote by
![]() $\Gamma ^{(n)}$
the graph of
$\Gamma ^{(n)}$
the graph of
![]() $F^n$
and by
$F^n$
and by
the diagonal in
![]() $X\times X$
. Then the set of periodic points of F of period n is defined as the set
$X\times X$
. Then the set of periodic points of F of period n is defined as the set
and for
![]() $z\in \operatorname {Per}_n(F)$
, we define the multiplicity of z as a periodic point of F of order n to be the number
$z\in \operatorname {Per}_n(F)$
, we define the multiplicity of z as a periodic point of F of order n to be the number
, defined in §2.1.
Another source of motivation is whether or not periodic points equidistribute. In [Reference Ljubich24], Ljubich showed that this is the case for rational maps of degree bigger than or equal to
![]() $2$
, where periodic points are counted either with or without multiplicity. The equidistribution of periodic points is also studied in [Reference Briend and Duval2, Reference Dinh, Nguyen and Truong16, Reference Favre and Rivera-Letelier19] in the case of maps, and in [Reference Dinh13, Reference Dinh14] in the case of correspondences. We prove this holds for the family
$2$
, where periodic points are counted either with or without multiplicity. The equidistribution of periodic points is also studied in [Reference Briend and Duval2, Reference Dinh, Nguyen and Truong16, Reference Favre and Rivera-Letelier19] in the case of maps, and in [Reference Dinh13, Reference Dinh14] in the case of correspondences. We prove this holds for the family
![]() $\lbrace \mathcal {F}_a\rbrace _{a\in \mathcal {K}}$
as well.
$\lbrace \mathcal {F}_a\rbrace _{a\in \mathcal {K}}$
as well.
Theorem 1.3. For
![]() $a\in \mathcal {K}$
,
$a\in \mathcal {K}$
,

are both weakly convergent to
![]() $\tfrac 12(\mu _-+\mu _+)$
, as
$\tfrac 12(\mu _-+\mu _+)$
, as
![]() $n\to \infty $
.
$n\to \infty $
.
In §5, we define the set
![]() $\hat {P}^{\Gamma }_n$
of superstable parameters of order n. Combining the main results of [Reference Bullett and Lomonaco5, Reference Petersen and Roesch29], we obtain a homeomorphism
$\hat {P}^{\Gamma }_n$
of superstable parameters of order n. Combining the main results of [Reference Bullett and Lomonaco5, Reference Petersen and Roesch29], we obtain a homeomorphism
![]() $\Psi :\mathcal {M}\to \mathcal {M}_{\Gamma }$
between the Mandelbrot set
$\Psi :\mathcal {M}\to \mathcal {M}_{\Gamma }$
between the Mandelbrot set
![]() $\mathcal {M}$
and the connectedness locus
$\mathcal {M}$
and the connectedness locus
![]() $\mathcal {M}_{\Gamma }$
of the family
$\mathcal {M}_{\Gamma }$
of the family
![]() $\lbrace \mathcal {F}_a\rbrace _{a\in \mathcal {K}}$
. These results, together with the equidistribution result in [Reference Levin23], yield the following theorem.
$\lbrace \mathcal {F}_a\rbrace _{a\in \mathcal {K}}$
. These results, together with the equidistribution result in [Reference Levin23], yield the following theorem.
Theorem 1.4. In
![]() $\mathcal {M}_{\Gamma }$
, superstable parameters equidistribute with respect to
$\mathcal {M}_{\Gamma }$
, superstable parameters equidistribute with respect to
![]() $\Psi ^*m_{\operatorname {BIF}}$
, that is,
$\Psi ^*m_{\operatorname {BIF}}$
, that is,
 $$ \begin{align*}\lim\limits_{n\to\infty}\frac{1}{2^{n-1}}\sum\limits_{a\in\hat{P}^{\Gamma}_n}\delta_a=\Psi^*m_{\operatorname{BIF}}.\end{align*} $$
$$ \begin{align*}\lim\limits_{n\to\infty}\frac{1}{2^{n-1}}\sum\limits_{a\in\hat{P}^{\Gamma}_n}\delta_a=\Psi^*m_{\operatorname{BIF}}.\end{align*} $$
1.1 Notes and references
There is a bigger family studied by Bullett and Harvey in [Reference Bullett and Harvey8], given by replacing the right-hand side of equation (1) by
![]() $3k$
, where
$3k$
, where
![]() $k\in \mathbb {C}$
. For these correspondences, it is also possible to define limit sets
$k\in \mathbb {C}$
. For these correspondences, it is also possible to define limit sets
![]() $\Lambda _{a,k,-}$
and
$\Lambda _{a,k,-}$
and
![]() $\Lambda _{a,k,+}$
analogous to those in the case where
$\Lambda _{a,k,+}$
analogous to those in the case where
![]() $k=1$
. In [Reference Bharali and Sridharan1], Bharali and Sridharan show how their equidistribution result applies to these correspondences in the case where
$k=1$
. In [Reference Bharali and Sridharan1], Bharali and Sridharan show how their equidistribution result applies to these correspondences in the case where
![]() $\Lambda _{a,k,-}$
is a repeller. Parameters for which this is the case exist from the results in [Reference Bullett and Harvey8]. However, we prove in Theorem 1.1 part
$\Lambda _{a,k,-}$
is a repeller. Parameters for which this is the case exist from the results in [Reference Bullett and Harvey8]. However, we prove in Theorem 1.1 part
![]() $(2)$
that this is never the case when
$(2)$
that this is never the case when
![]() $k=1$
and
$k=1$
and
![]() $a\in \mathcal {K}$
.
$a\in \mathcal {K}$
.
1.2 Organization
The structure of this paper is as follows. In §2.1, we give an introduction to holomorphic correspondences and their action on Borel measures. In §2.2, we introduce the correspondences
![]() $\mathcal {F}_a$
given by equation (1). We define critical values and find those of
$\mathcal {F}_a$
given by equation (1). We define critical values and find those of
![]() $\mathcal {F}_a$
in §2.3, and define Klein combination pair and the Klein combination locus
$\mathcal {F}_a$
in §2.3, and define Klein combination pair and the Klein combination locus
![]() $\mathcal {K}$
in §2.4. In §3.1, we define modular and weakly modular correspondences, and prove part
$\mathcal {K}$
in §2.4. In §3.1, we define modular and weakly modular correspondences, and prove part
![]() $(1)$
of Theorem 1.1. To prove that
$(1)$
of Theorem 1.1. To prove that
![]() $\mathcal {F}_a$
is weakly modular, we use the decomposition
$\mathcal {F}_a$
is weakly modular, we use the decomposition
![]() $\mathcal {F}_a=\operatorname {J}_a\circ \operatorname {Cov^Q_0}$
, given in [Reference Bullett and Lomonaco4], into a certain involution
$\mathcal {F}_a=\operatorname {J}_a\circ \operatorname {Cov^Q_0}$
, given in [Reference Bullett and Lomonaco4], into a certain involution
![]() $\operatorname {J}_a$
composed with the deleted covering correspondence
$\operatorname {J}_a$
composed with the deleted covering correspondence
![]() $\operatorname {Cov^Q_0}$
described in §2.2, and construct the measures in the definition of weakly modular using the symmetry of the graph of
$\operatorname {Cov^Q_0}$
described in §2.2, and construct the measures in the definition of weakly modular using the symmetry of the graph of
![]() $\operatorname {Cov^Q_0}$
. The fact that
$\operatorname {Cov^Q_0}$
. The fact that
![]() $\mathcal {F}_a$
is not modular follows from the fact that Borel measures assigning positive measure to non-empty open sets are not invariant by
$\mathcal {F}_a$
is not modular follows from the fact that Borel measures assigning positive measure to non-empty open sets are not invariant by
![]() $\mathcal {F}_a$
. In §3.2, we define the limit sets
$\mathcal {F}_a$
. In §3.2, we define the limit sets
![]() $\Lambda _{a,-}$
and
$\Lambda _{a,-}$
and
![]() $\Lambda _{a,+}$
, and prove part
$\Lambda _{a,+}$
, and prove part
![]() $(2)$
of Theorem 1.1 by showing that the parabolic fixed point in
$(2)$
of Theorem 1.1 by showing that the parabolic fixed point in
![]() $\partial \Lambda _{a,-}$
violates the definition of a repeller. In §4, we describe the exceptional set of the two-sided restriction
$\partial \Lambda _{a,-}$
violates the definition of a repeller. In §4, we describe the exceptional set of the two-sided restriction
![]() $f_a$
and the set
$f_a$
and the set
![]() $\operatorname {Per}_n(\mathcal {F}_a)$
of periodic points of period n. Finally, in §5, we use the description of
$\operatorname {Per}_n(\mathcal {F}_a)$
of periodic points of period n. Finally, in §5, we use the description of
![]() $f_a$
given in [Reference Bullett and Lomonaco4] together with the results in [Reference Freire, Lopes and Mañé20, Reference Ljubich24] to prove Theorems 1.2 and 1.3 about asymptotic equidistribution of images, preimages, and periodic points. We finish with the proof of Theorem 1.4 about equidistribution of special points in the modular Mandelbrot set
$f_a$
given in [Reference Bullett and Lomonaco4] together with the results in [Reference Freire, Lopes and Mañé20, Reference Ljubich24] to prove Theorems 1.2 and 1.3 about asymptotic equidistribution of images, preimages, and periodic points. We finish with the proof of Theorem 1.4 about equidistribution of special points in the modular Mandelbrot set
![]() $\mathcal {M}_{\Gamma }$
.
$\mathcal {M}_{\Gamma }$
.
2 Preliminaries
2.1 Holomorphic correspondences
Let X be a compact Riemann surface and let
![]() $\pi _j:X\times X\to X$
be the canonical projection to the jth coordinate,
$\pi _j:X\times X\to X$
be the canonical projection to the jth coordinate,
![]() $j=1,2$
. We say that a formal sum
$j=1,2$
. We say that a formal sum
![]() $\Gamma =\sum _i n_i\Gamma (i)$
is a holomorphic 1-chain on
$\Gamma =\sum _i n_i\Gamma (i)$
is a holomorphic 1-chain on
![]() $X\times X$
if its support
$X\times X$
if its support
![]() is a subvariety of
is a subvariety of
![]() $X\times X$
of pure dimension
$X\times X$
of pure dimension
![]() $1$
whose irreducible components are exactly the
$1$
whose irreducible components are exactly the
![]() $\Gamma (i)$
, and the
$\Gamma (i)$
, and the
![]() $n_i$
are non-negative integers. We say that the
$n_i$
are non-negative integers. We say that the
![]() $\Gamma (i)$
are the irreducible components of
$\Gamma (i)$
are the irreducible components of
![]() $\Gamma $
.
$\Gamma $
.
Let
![]() $\Gamma =\sum _in_i\Gamma (i)$
be a holomorphic 1-chain satisfying that for
$\Gamma =\sum _in_i\Gamma (i)$
be a holomorphic 1-chain satisfying that for
![]() $j=1,2$
and every i such that
$j=1,2$
and every i such that
![]() $n_i>0$
, the restriction
$n_i>0$
, the restriction
of the canonical projection
![]() $X\times X\to X$
to the irreducible component
$X\times X\to X$
to the irreducible component
![]() $\Gamma (i)$
is surjective. The chain
$\Gamma (i)$
is surjective. The chain
![]() $\Gamma $
induces a multivalued map F from X to itself by
$\Gamma $
induces a multivalued map F from X to itself by
The multivalued map F is called a holomorphic correspondence and it is said to be irreducible if
![]() $\sum _i n_i=1$
. We say that
$\sum _i n_i=1$
. We say that
is the graph of the holomorphic correspondence F. Let
![]() $\iota :X\times X\to X\times X$
be the involution
$\iota :X\times X\to X\times X$
be the involution
![]() $(z,w)\mapsto (w,z)$
. We can define the adjoint correspondence
$(z,w)\mapsto (w,z)$
. We can define the adjoint correspondence
![]() $F^{-1}$
of F by the relation
$F^{-1}$
of F by the relation
, which is a holomorphic correspondence, whose graph is the holomorphic 1-chain
![]() $\Gamma _F^{-1}=\sum _in_i\iota (\Gamma (i))$
.
$\Gamma _F^{-1}=\sum _in_i\iota (\Gamma (i))$
.
In [Reference Stoll30], Stoll introduced a notion of multiplicity that will be useful for this paper. Let M be a quasi-projective variety and N a smooth quasi-projective variety. If
![]() $g:M\to N$
is regular, and
$g:M\to N$
is regular, and
![]() $a\in M$
, then we say that a neighborhood U of a is distinguished with respect to g and a if
$a\in M$
, then we say that a neighborhood U of a is distinguished with respect to g and a if
![]() $\overline {U}$
is compact and
$\overline {U}$
is compact and
![]() $g^{-1}(g(a))\cap \overline {U}=\lbrace a\rbrace $
. Such neighborhoods exist if and only if
$g^{-1}(g(a))\cap \overline {U}=\lbrace a\rbrace $
. Such neighborhoods exist if and only if
![]() $\dim _a g^{-1}(g(a))=0$
and, in this case, they form a base of neighborhoods. If U is distinguished with respect to g and a, then put
$\dim _a g^{-1}(g(a))=0$
and, in this case, they form a base of neighborhoods. If U is distinguished with respect to g and a, then put
![]() . It can be shown that
. It can be shown that
![]() does not depend on the distinguished neighborhood U, and the maps
does not depend on the distinguished neighborhood U, and the maps
![]() $n_b$
defined on N by
$n_b$
defined on N by
![]() $a\mapsto \sum \nolimits _{b\in g^{-1}(a)}\hat {\nu }_g(b)$
are constant in each component.
$a\mapsto \sum \nolimits _{b\in g^{-1}(a)}\hat {\nu }_g(b)$
are constant in each component.
Suppose that
![]() $g:M\to N$
is a finite and surjective regular map, with M and N as above. Stoll proved in [Reference Stoll30] that
$g:M\to N$
is a finite and surjective regular map, with M and N as above. Stoll proved in [Reference Stoll30] that
![]() $\hat {\nu }_g(a)$
generalizes the notion of multiplicity of g at a and whenever
$\hat {\nu }_g(a)$
generalizes the notion of multiplicity of g at a and whenever
![]() $\varphi $
is a continuous function with compact support in M, the map
$\varphi $
is a continuous function with compact support in M, the map
 $$ \begin{align*}a\mapsto\sum\limits_{b\in g^{-1}(a)}\hat{\nu}_g(b)\varphi(b)\end{align*} $$
$$ \begin{align*}a\mapsto\sum\limits_{b\in g^{-1}(a)}\hat{\nu}_g(b)\varphi(b)\end{align*} $$
is continuous.
To study dynamics, we proceed to define the composition of two holomorphic correspondences F and G with associated holomorphic 1-chains
![]() $\Gamma _F=\sum _i n_i\Gamma _F(i)$
and
$\Gamma _F=\sum _i n_i\Gamma _F(i)$
and
![]() $\Gamma _G=\sum _j m_j\Gamma _G(j)$
, respectively. For each i and j, let
$\Gamma _G=\sum _j m_j\Gamma _G(j)$
, respectively. For each i and j, let
![]() $A_{i,j}$
be the image of the projection
$A_{i,j}$
be the image of the projection
![]() $p_{i,j}:(\Gamma _G(j)\times \Gamma _F(i))\cap \lbrace x_2=x_3\rbrace \hookrightarrow X\times X$
that forgets the second and third coordinates, i.e.,
$p_{i,j}:(\Gamma _G(j)\times \Gamma _F(i))\cap \lbrace x_2=x_3\rbrace \hookrightarrow X\times X$
that forgets the second and third coordinates, i.e.,
Let
![]() $\lbrace \Gamma (i,j,k)\rbrace _{k=1}^{N(i,j)}$
be the irreducible components of
$\lbrace \Gamma (i,j,k)\rbrace _{k=1}^{N(i,j)}$
be the irreducible components of
![]() $A_{i,j}$
. Observe that since
$A_{i,j}$
. Observe that since
![]() $\Gamma _G(j)$
and
$\Gamma _G(j)$
and
![]() $\Gamma _F(i)$
are both quasi-projective, and so is
$\Gamma _F(i)$
are both quasi-projective, and so is
![]() $\lbrace x_2=x_4\rbrace \subset X^4$
, then
$\lbrace x_2=x_4\rbrace \subset X^4$
, then
![]() $p_{i,j}$
is a regular map from the quasi-projective variety
$p_{i,j}$
is a regular map from the quasi-projective variety
![]() $(\Gamma _G(j)\times \Gamma _F(i))\cap \lbrace x_2=x_3\rbrace $
to the smooth quasi-projective variety
$(\Gamma _G(j)\times \Gamma _F(i))\cap \lbrace x_2=x_3\rbrace $
to the smooth quasi-projective variety
![]() $X\times X$
. Then we have that the map
$X\times X$
. Then we have that the map
defined on
![]() $\Gamma (i,j,k)$
is constant. Therefore,
$\Gamma (i,j,k)$
is constant. Therefore,
denotes the number of
![]() $x\in X$
such that
$x\in X$
such that
![]() $((z,x),(x,w))\in \Gamma _G(j)\times \Gamma _F(i)$
, for a generic point
$((z,x),(x,w))\in \Gamma _G(j)\times \Gamma _F(i)$
, for a generic point
![]() $(z,w)\in \Gamma (i,j,k)$
. Define the composition
$(z,w)\in \Gamma (i,j,k)$
. Define the composition
![]() $F\circ G$
as the holomorphic correspondence determined by the holomorphic 1-chain
$F\circ G$
as the holomorphic correspondence determined by the holomorphic 1-chain

Note that the
![]() $\operatorname {supp}\Gamma _{F\circ G}=\bigcup _{i,j}A_{i,j}$
.
$\operatorname {supp}\Gamma _{F\circ G}=\bigcup _{i,j}A_{i,j}$
.
Set
![]() . We have that
. We have that
![]() $d(F\circ G)=d(F)d(G)$
. Thus, in particular, for every integer
$d(F\circ G)=d(F)d(G)$
. Thus, in particular, for every integer
![]() $n\geq 1$
, we have that
$n\geq 1$
, we have that
![]() $d(F^n)=(d(F))^n$
. We call
$d(F^n)=(d(F))^n$
. We call
![]() $d(F)$
the topological degree of F, and it corresponds to the number of preimages of a generic point under F.
$d(F)$
the topological degree of F, and it corresponds to the number of preimages of a generic point under F.
If F is an irreducible holomorphic correspondence over X with graph
![]() $\Gamma $
and
$\Gamma $
and
![]() $\varphi :X\to \mathbb {C}$
is a continuous function, then
$\varphi :X\to \mathbb {C}$
is a continuous function, then

is continuous as well, see [Reference Clozel and Ullmo11, Lemma 1.1]. Now let F be a holomorphic correspondence that is not necessarily irreducible, with graph
![]() $\Gamma _F=\sum _i n_i\Gamma (i)$
. We denote by
$\Gamma _F=\sum _i n_i\Gamma (i)$
. We denote by
![]() $F_i$
the holomorphic correspondence induced by
$F_i$
the holomorphic correspondence induced by
![]() $\Gamma (i)$
and we put
$\Gamma (i)$
and we put

and
. Then for every continuous function
![]() $\varphi :X\to \mathbb {C}$
, the map
$\varphi :X\to \mathbb {C}$
, the map
 $$ \begin{align*} z\mapsto\sum\limits_{w\in F(z)}\nu_{F}(z,w)\varphi(w)&=\sum\limits_{w\in f(z)}\bigg(\sum\limits_i n_i\nu_{F_i}(z,w)\bigg)\varphi(w)\\ &=\sum\limits_i n_i {F_i}_*\varphi(w) \end{align*} $$
$$ \begin{align*} z\mapsto\sum\limits_{w\in F(z)}\nu_{F}(z,w)\varphi(w)&=\sum\limits_{w\in f(z)}\bigg(\sum\limits_i n_i\nu_{F_i}(z,w)\bigg)\varphi(w)\\ &=\sum\limits_i n_i {F_i}_*\varphi(w) \end{align*} $$
is also continuous.
The holomorphic correspondence F induces an action
![]() $F_*$
on finite Borel measures
$F_*$
on finite Borel measures
![]() $\mu $
by duality, namely
$\mu $
by duality, namely
, called the push-forward operator and the resultant measure
![]() $F_*\mu $
is the push-forward measure of
$F_*\mu $
is the push-forward measure of
![]() $\mu $
under F. We define as well the action
$\mu $
under F. We define as well the action
, called the pull-back operator and the resultant measure
![]() $F^*\mu $
is called the pull-back measure of
$F^*\mu $
is called the pull-back measure of
![]() $\mu $
under F. This action on measures agrees with the action on points
$\mu $
under F. This action on measures agrees with the action on points
where
![]() $\delta _z$
is the Dirac delta at z.
$\delta _z$
is the Dirac delta at z.
To see this, note that for every continuous function
![]() $\varphi :X\to \mathbb {C}$
,
$\varphi :X\to \mathbb {C}$
,
 $$ \begin{align*} \bigg\langle\sum\limits_{w\in F(z)}\nu_{F}(z,w)\delta_w,\varphi\bigg\rangle&=\sum\limits_{w\in F(z)}\nu_{F}(z,w)\langle\delta_w,\varphi\rangle\\ &=\sum\limits_{w\in F(z)}\nu_{F}(z,w)\varphi(w)\\ &=\int\bigg(\sum\limits_{w\in F(\zeta)}\nu_{F}(\zeta,w)\varphi(w)\bigg)d\delta_z(\zeta)\\ &=\langle\delta_z,F_*\varphi\rangle\\ &=\langle F^*\delta_z,\varphi\rangle. \end{align*} $$
$$ \begin{align*} \bigg\langle\sum\limits_{w\in F(z)}\nu_{F}(z,w)\delta_w,\varphi\bigg\rangle&=\sum\limits_{w\in F(z)}\nu_{F}(z,w)\langle\delta_w,\varphi\rangle\\ &=\sum\limits_{w\in F(z)}\nu_{F}(z,w)\varphi(w)\\ &=\int\bigg(\sum\limits_{w\in F(\zeta)}\nu_{F}(\zeta,w)\varphi(w)\bigg)d\delta_z(\zeta)\\ &=\langle\delta_z,F_*\varphi\rangle\\ &=\langle F^*\delta_z,\varphi\rangle. \end{align*} $$
2.2 The family
 $\lbrace \mathcal {F}_a\rbrace _a$
$\lbrace \mathcal {F}_a\rbrace _a$
Let
![]() $Q(z)\in \mathbb {C}[z]$
be a nonlinear polynomial. The deleted covering relation of Q on
$Q(z)\in \mathbb {C}[z]$
be a nonlinear polynomial. The deleted covering relation of Q on
![]() $\mathbb {C}\times \mathbb {C}$
is defined by
$\mathbb {C}\times \mathbb {C}$
is defined by
![]() $w\in \operatorname {Cov^Q_0}(z)$
if and only if
$w\in \operatorname {Cov^Q_0}(z)$
if and only if
Note that the denominator ‘deletes’ the obvious association of z with itself in the equation
![]() $Q(z)=Q(w)$
.
$Q(z)=Q(w)$
.
In this section, we will identify
![]() $\widehat {\mathbb {C}}$
with the complex projective line when it is convenient to work with homogeneous coordinates
$\widehat {\mathbb {C}}$
with the complex projective line when it is convenient to work with homogeneous coordinates
![]() $(z:w)$
.
$(z:w)$
.
Proposition 2.1. Put
![]() . The closure of the relation in equation (2) is an irreducible quasiprojective complex variety
. The closure of the relation in equation (2) is an irreducible quasiprojective complex variety
![]() $\Gamma _0$
of
$\Gamma _0$
of
![]() $\widehat {\mathbb {C}}\times \widehat {\mathbb {C}}$
of dimension
$\widehat {\mathbb {C}}\times \widehat {\mathbb {C}}$
of dimension
![]() $1$
. Moreover, the projections
$1$
. Moreover, the projections
![]() and
and
![]() are both surjective and of degree
are both surjective and of degree
![]() $2$
.
$2$
.
Proof. Note that
![]() $P_Q(z,w)=z^2+zw+w^2-3$
and consider
$P_Q(z,w)=z^2+zw+w^2-3$
and consider
![]() $P_Q(z,w)$
as a single variable polynomial in
$P_Q(z,w)$
as a single variable polynomial in
![]() $(\mathbb {C}[z])[w]$
. Then its discriminant
$(\mathbb {C}[z])[w]$
. Then its discriminant
![]() $-3z^2+12$
is not a square in
$-3z^2+12$
is not a square in
![]() $\mathbb {C}[z]$
. Therefore,
$\mathbb {C}[z]$
. Therefore,
![]() $P_Q(z,w)$
is an irreducible polynomial, and hence
$P_Q(z,w)$
is an irreducible polynomial, and hence
is an irreducible subvariety of
![]() $\mathbb {C}\times \mathbb {C}$
.
$\mathbb {C}\times \mathbb {C}$
.
Now we want to describe the closure
![]() $\overline {\mathcal {Z}}$
of
$\overline {\mathcal {Z}}$
of
![]() $\mathcal {Z}$
in
$\mathcal {Z}$
in
![]() $\widehat {\mathbb {C}}\times \widehat {\mathbb {C}}$
. Observe that if we fix
$\widehat {\mathbb {C}}\times \widehat {\mathbb {C}}$
. Observe that if we fix
![]() $z\in \mathbb {C}$
, then
$z\in \mathbb {C}$
, then
![]() $\lim \nolimits _{w\to \infty }P_Q(z,w)=\infty $
, and if we fix
$\lim \nolimits _{w\to \infty }P_Q(z,w)=\infty $
, and if we fix
![]() $w\in \mathbb {C}$
, then
$w\in \mathbb {C}$
, then
![]() $\lim \nolimits _{z\to \infty }P_Q(z,w)=\infty $
. Therefore, there are no points of the form
$\lim \nolimits _{z\to \infty }P_Q(z,w)=\infty $
. Therefore, there are no points of the form
![]() $(z,\infty )$
or
$(z,\infty )$
or
![]() $(\infty , w)$
in
$(\infty , w)$
in
![]() $\overline {\mathcal {Z}}$
. Given
$\overline {\mathcal {Z}}$
. Given
![]() $R>0$
, let
$R>0$
, let
![]() $z\in \mathbb {C}$
be such that
$z\in \mathbb {C}$
be such that
![]() $|z|=R$
. Observe that
$|z|=R$
. Observe that
![]() $P_Q(z,\cdot )\in \mathbb {C}[w]$
is non-constant and therefore has at least one root in
$P_Q(z,\cdot )\in \mathbb {C}[w]$
is non-constant and therefore has at least one root in
![]() $\mathbb {C}$
. Let
$\mathbb {C}$
. Let
![]() $w\in \mathbb {C}$
be a root. Then
$w\in \mathbb {C}$
be a root. Then
![]() $(z,w)\in \mathcal {Z}$
and we have that
$(z,w)\in \mathcal {Z}$
and we have that
![]() $|w^3-3w|=|Q(w)|=|Q(z)|=|z^3-3z|\geq R^3-3R$
. By taking
$|w^3-3w|=|Q(w)|=|Q(z)|=|z^3-3z|\geq R^3-3R$
. By taking
![]() $R\to \infty $
, we get that
$R\to \infty $
, we get that
![]() $(z,w)\to (\infty ,\infty )$
. Therefore,
$(z,w)\to (\infty ,\infty )$
. Therefore,
![]() $\overline {\mathcal {Z}}=\mathcal {Z}\cup \lbrace (\infty ,\infty )\rbrace $
. In particular,
$\overline {\mathcal {Z}}=\mathcal {Z}\cup \lbrace (\infty ,\infty )\rbrace $
. In particular,
![]() $\overline {\mathcal {Z}}$
extends the relation given by equation (2) from
$\overline {\mathcal {Z}}$
extends the relation given by equation (2) from
![]() $\mathbb {C}\times \mathbb {C}$
to
$\mathbb {C}\times \mathbb {C}$
to
![]() $\widehat {\mathbb {C}}\times \widehat {\mathbb {C}}$
.
$\widehat {\mathbb {C}}\times \widehat {\mathbb {C}}$
.
Take the homogenization
of
![]() $P_Q(z,w)$
, so
$P_Q(z,w)$
, so
![]() $P_Q(z,w)=T(z,1,w,1)$
, and note that
$P_Q(z,w)=T(z,1,w,1)$
, and note that
![]() $T(\unicode{x3bb} _1z,\unicode{x3bb} _1x,\unicode{x3bb} _2w,\unicode{x3bb} _2y)=\unicode{x3bb} _1^2\unicode{x3bb} _2^2T(z,x,w,y)$
. Thus, for the closed subvariety
$T(\unicode{x3bb} _1z,\unicode{x3bb} _1x,\unicode{x3bb} _2w,\unicode{x3bb} _2y)=\unicode{x3bb} _1^2\unicode{x3bb} _2^2T(z,x,w,y)$
. Thus, for the closed subvariety
of
![]() $\widehat {\mathbb {C}}\times \widehat {\mathbb {C}}$
, we have that
$\widehat {\mathbb {C}}\times \widehat {\mathbb {C}}$
, we have that
![]() $\Gamma _0=\overline {\mathcal {Z}}$
. To prove that
$\Gamma _0=\overline {\mathcal {Z}}$
. To prove that
![]() $\Gamma _0$
is irreducible, note that each of its irreducible components intersecting
$\Gamma _0$
is irreducible, note that each of its irreducible components intersecting
![]() $\mathbb {C}\times \mathbb {C}$
must be a closed subset of
$\mathbb {C}\times \mathbb {C}$
must be a closed subset of
![]() $\Gamma _0$
containing
$\Gamma _0$
containing
![]() $\Gamma _0\cap (\mathbb {C}\times \mathbb {C})=\mathcal {Z}$
, and therefore it is
$\Gamma _0\cap (\mathbb {C}\times \mathbb {C})=\mathcal {Z}$
, and therefore it is
![]() $\Gamma _0$
itself. Thus,
$\Gamma _0$
itself. Thus,
![]() $\Gamma _0$
has only one irreducible component and hence it is irreducible.
$\Gamma _0$
has only one irreducible component and hence it is irreducible.
We proceed to show
![]() $\Gamma _0$
has dimension 1. Observe that the polynomial
$\Gamma _0$
has dimension 1. Observe that the polynomial
![]() $T(z,x,w,y)$
is irreducible in
$T(z,x,w,y)$
is irreducible in
![]() $\mathbb {C}[z,x,w,y]$
, as whenever
$\mathbb {C}[z,x,w,y]$
, as whenever
![]() $S(z,x,w,y)|T(z,x,w,y)$
in
$S(z,x,w,y)|T(z,x,w,y)$
in
![]() $\mathbb {C}[z,x,w,y]$
, then
$\mathbb {C}[z,x,w,y]$
, then
![]() $S(z,1,w,1)|P_Q(z,w)$
in
$S(z,1,w,1)|P_Q(z,w)$
in
![]() $\mathbb {C}[z,w]$
. Therefore, the zero set
$\mathbb {C}[z,w]$
. Therefore, the zero set
![]() $Z(T)\subset \mathbb {C}^2\times \mathbb {C}^2$
of T is an irreducible hypersurface of
$Z(T)\subset \mathbb {C}^2\times \mathbb {C}^2$
of T is an irreducible hypersurface of
![]() $\mathbb {C}^2\times \mathbb {C}^2$
, and hence it has codimension 1. Now let
$\mathbb {C}^2\times \mathbb {C}^2$
, and hence it has codimension 1. Now let
![]() $p:\mathbb {C}^2\setminus \lbrace (0,0)\rbrace \to \widehat {\mathbb {C}}$
be the projection sending
$p:\mathbb {C}^2\setminus \lbrace (0,0)\rbrace \to \widehat {\mathbb {C}}$
be the projection sending
![]() $(z,x)\mapsto (z:x)$
. Note that in the chart
$(z,x)\mapsto (z:x)$
. Note that in the chart
the map p is simply
![]() $(z,w)\mapsto (z/w:1)$
, and in the chart
$(z,w)\mapsto (z/w:1)$
, and in the chart
it becomes
![]() $(z,w)\mapsto (1:w/z)$
. Let
$(z,w)\mapsto (1:w/z)$
. Let
![]() $\hat {p}:(\mathbb {C}^2\setminus \lbrace (0,0)\rbrace )\times (\mathbb {C}^2\setminus \lbrace (0,0)\rbrace )\to \widehat {\mathbb {C}}\times \widehat {\mathbb {C}}$
be the map defined by
$\hat {p}:(\mathbb {C}^2\setminus \lbrace (0,0)\rbrace )\times (\mathbb {C}^2\setminus \lbrace (0,0)\rbrace )\to \widehat {\mathbb {C}}\times \widehat {\mathbb {C}}$
be the map defined by
. Then
is a regular map between irreducible varieties, and
has constant fiber dimension equal to 2, as T is homogeneous in
![]() $(z,x)$
and in
$(z,x)$
and in
![]() $(w,y)$
. Therefore,
$(w,y)$
. Therefore,
Finally, observe that the polynomial equation (2) has at least one and at most two solutions for every
![]() $z\in \mathbb {C}$
, and by symmetry, the same holds for
$z\in \mathbb {C}$
, and by symmetry, the same holds for
![]() $w\in \mathbb {C}$
. Note as well that
$w\in \mathbb {C}$
. Note as well that
![]() $\infty $
is in correspondence with and only with itself. Thus, the projections
$\infty $
is in correspondence with and only with itself. Thus, the projections
![]() and
and
![]() are both surjective. Moreover,
are both surjective. Moreover,
![]() $P_Q(1,1)=P_Q(1,-2)=0$
, and hence
$P_Q(1,1)=P_Q(1,-2)=0$
, and hence
![]() $P_Q(1,w)$
has exactly two solutions. Therefore,
$P_Q(1,w)$
has exactly two solutions. Therefore,
![]() .
.
Remark 2.2. Proposition 2.1 holds for a large class of polynomials
![]() $Q(z)$
. Observe that no polynomial can have
$Q(z)$
. Observe that no polynomial can have
![]() $Q(z)=Q(\infty )$
for a finite number z. Therefore, following the proof of Proposition 2.1, we conclude that to get an irreducible holomorphic correspondence, it suffices to prove that
$Q(z)=Q(\infty )$
for a finite number z. Therefore, following the proof of Proposition 2.1, we conclude that to get an irreducible holomorphic correspondence, it suffices to prove that
![]() $P_Q(z,w)$
is irreducible over
$P_Q(z,w)$
is irreducible over
![]() $\mathbb {C}$
. This holds under fairly general conditions. For instance, this is the case when Q is indecomposable and not linearly related to either
$\mathbb {C}$
. This holds under fairly general conditions. For instance, this is the case when Q is indecomposable and not linearly related to either
![]() $z^n$
or a Chebyshev polynomial (see [Reference Fried21]).
$z^n$
or a Chebyshev polynomial (see [Reference Fried21]).
On the other hand, note that whenever
![]() $Q=R\circ S$
with R and S of degree greater than
$Q=R\circ S$
with R and S of degree greater than
![]() $1$
, then
$1$
, then
![]() $P_S(z,w)$
divides
$P_S(z,w)$
divides
![]() $P_Q(z,w)$
, and therefore
$P_Q(z,w)$
, and therefore
![]() $P_Q(z,w)$
is reducible.
$P_Q(z,w)$
is reducible.
Proposition 2.1 says that
![]() $\Gamma _0$
is the graph of an irreducible holomorphic correspondence, where
$\Gamma _0$
is the graph of an irreducible holomorphic correspondence, where
![]() $\Gamma _0$
is a quasi-projective variety and
$\Gamma _0$
is a quasi-projective variety and
![]() is a finite and surjective morphism over
is a finite and surjective morphism over
![]() $\mathbb {C}$
, and hence we can use our definition of pull-back and push-forward operators induced by the correspondence on finite measures. We call this correspondence the deleted covering correspondence of Q, denoted by
$\mathbb {C}$
, and hence we can use our definition of pull-back and push-forward operators induced by the correspondence on finite measures. We call this correspondence the deleted covering correspondence of Q, denoted by
![]() $\operatorname {Cov^Q_0}$
as well. That is,
$\operatorname {Cov^Q_0}$
as well. That is,
![]() $\operatorname {Cov^Q_0}$
is the holomorphic correspondence on
$\operatorname {Cov^Q_0}$
is the holomorphic correspondence on
![]() $\widehat {\mathbb {C}}\times \widehat {\mathbb {C}}$
such that
$\widehat {\mathbb {C}}\times \widehat {\mathbb {C}}$
such that
![]() $\Gamma _{\operatorname {Cov^Q_0}}=\Gamma _0$
. From now on, we always consider
$\Gamma _{\operatorname {Cov^Q_0}}=\Gamma _0$
. From now on, we always consider
![]() $Q(z)=z^3-3z$
.
$Q(z)=z^3-3z$
.
Now take
![]() $a\in \mathbb {C}\setminus \lbrace 1\rbrace $
and let
$a\in \mathbb {C}\setminus \lbrace 1\rbrace $
and let
![]() $\operatorname {J}_a:\widehat {\mathbb {C}}\to \widehat {\mathbb {C}}$
be the involution
$\operatorname {J}_a:\widehat {\mathbb {C}}\to \widehat {\mathbb {C}}$
be the involution
The composition of
![]() $\operatorname {Cov^Q_0}$
with the involution
$\operatorname {Cov^Q_0}$
with the involution
![]() $\operatorname {J}_a$
is again an irreducible holomorphic correspondence
$\operatorname {J}_a$
is again an irreducible holomorphic correspondence
on
![]() $\widehat {\mathbb {C}}\times \widehat {\mathbb {C}}$
with graph
$\widehat {\mathbb {C}}\times \widehat {\mathbb {C}}$
with graph
![]() $\Gamma _a$
for which we can use the pull-back and push-forward operators above as well. Note that
$\Gamma _a$
for which we can use the pull-back and push-forward operators above as well. Note that
![]() $d(\mathcal {F}_a)=d(\mathcal {F}_a^{-1})=2$
and
$d(\mathcal {F}_a)=d(\mathcal {F}_a^{-1})=2$
and
![]() $\mathcal {F}_a^{-1}=\operatorname {Cov^Q_0}\circ \operatorname {J}_a=\operatorname {J}_a\circ \mathcal {F}_a\circ \operatorname {J}_a$
, since
$\mathcal {F}_a^{-1}=\operatorname {Cov^Q_0}\circ \operatorname {J}_a=\operatorname {J}_a\circ \mathcal {F}_a\circ \operatorname {J}_a$
, since
![]() $\operatorname {Cov^Q_0}^{-1}=\operatorname {Cov^Q_0}$
and
$\operatorname {Cov^Q_0}^{-1}=\operatorname {Cov^Q_0}$
and
![]() $\operatorname {J}_a^{-1}=\operatorname {J}_a$
.
$\operatorname {J}_a^{-1}=\operatorname {J}_a$
.
Set
![]() . Then
. Then
![]() $\phi _a^{-1}\circ \mathcal {F}_a\circ \phi _a$
is a holomorphic correspondence on
$\phi _a^{-1}\circ \mathcal {F}_a\circ \phi _a$
is a holomorphic correspondence on
![]() $\widehat {\mathbb {C}}\times \widehat {\mathbb {C}}$
that, restricted to
$\widehat {\mathbb {C}}\times \widehat {\mathbb {C}}$
that, restricted to
![]() $(\widehat {\mathbb {C}}\setminus \lbrace -1\rbrace )\times (\widehat {\mathbb {C}}\setminus \lbrace 1\rbrace )$
, induces the relation given by equation (1). Thus,
$(\widehat {\mathbb {C}}\setminus \lbrace -1\rbrace )\times (\widehat {\mathbb {C}}\setminus \lbrace 1\rbrace )$
, induces the relation given by equation (1). Thus,
![]() $(z,w)\in (\widehat {\mathbb {C}}\setminus \lbrace -1\rbrace )\times (\widehat {\mathbb {C}}\setminus \lbrace 1\rbrace )$
satisfies equation (1) if and only if
$(z,w)\in (\widehat {\mathbb {C}}\setminus \lbrace -1\rbrace )\times (\widehat {\mathbb {C}}\setminus \lbrace 1\rbrace )$
satisfies equation (1) if and only if
![]() $w\in \mathcal {F}_a(z)$
[Reference Bullett and Lomonaco4, Lemma 3.1].
$w\in \mathcal {F}_a(z)$
[Reference Bullett and Lomonaco4, Lemma 3.1].
Observe that
![]() $\mathcal {F}_a^{-1}(1)=\operatorname {Cov^Q_0}(\operatorname {J}_a(1))=\operatorname {Cov^Q_0}(1)=\lbrace 1,-2\rbrace $
, independent of
$\mathcal {F}_a^{-1}(1)=\operatorname {Cov^Q_0}(\operatorname {J}_a(1))=\operatorname {Cov^Q_0}(1)=\lbrace 1,-2\rbrace $
, independent of
![]() $a\in \mathbb {C}\setminus \lbrace 1\rbrace $
. In particular,
$a\in \mathbb {C}\setminus \lbrace 1\rbrace $
. In particular,
![]() $1\in \operatorname {Per}_1(\mathcal {F}_a)$
and we say that
$1\in \operatorname {Per}_1(\mathcal {F}_a)$
and we say that
![]() $1$
is a fixed point of
$1$
is a fixed point of
![]() $\mathcal {F}_a$
.
$\mathcal {F}_a$
.
2.3 Critical values
In this section, we will discuss what parts of the graph of
![]() $\mathcal {F}_a$
are locally the graph of a holomorphic function, by defining and finding all critical values and ramification points of
$\mathcal {F}_a$
are locally the graph of a holomorphic function, by defining and finding all critical values and ramification points of
![]() $\Gamma _a$
. This will be used in §4 to find the exceptional set.
$\Gamma _a$
. This will be used in §4 to find the exceptional set.
Definition 2.3. Let
![]() $\Gamma $
be the graph of an irreducible holomorphic correspondence on
$\Gamma $
be the graph of an irreducible holomorphic correspondence on
![]() $\widehat {\mathbb {C}}$
, and put
$\widehat {\mathbb {C}}$
, and put
for
![]() $j=1,2$
and
$j=1,2$
and
We extend the definition to holomorphic 1-chains
![]() $\Gamma =\sum _i n_i\Gamma (i)$
by
$\Gamma =\sum _i n_i\Gamma (i)$
by
We call
![]() $A_2(\Gamma )$
the set of ramification points of the holomorphic correspondence associated to
$A_2(\Gamma )$
the set of ramification points of the holomorphic correspondence associated to
![]() $\Gamma $
, and
$\Gamma $
, and
![]() $B_2(\Gamma )$
the set of its critical values.
$B_2(\Gamma )$
the set of its critical values.
Note that
![]() $A_1(\Gamma )=\iota (A_2(\Gamma ^{-1}))$
and
$A_1(\Gamma )=\iota (A_2(\Gamma ^{-1}))$
and
![]() $A_2(\Gamma )=\iota (A_1(\Gamma ^{-1}))$
, where
$A_2(\Gamma )=\iota (A_1(\Gamma ^{-1}))$
, where
![]() $\iota :\widehat {\mathbb {C}}\times \widehat {\mathbb {C}}\to \widehat {\mathbb {C}}\times \widehat {\mathbb {C}}$
is the involution
$\iota :\widehat {\mathbb {C}}\times \widehat {\mathbb {C}}\to \widehat {\mathbb {C}}\times \widehat {\mathbb {C}}$
is the involution
![]() $\iota (z,w)=(w,z)$
.
$\iota (z,w)=(w,z)$
.
Suppose
![]() $\Gamma $
is the graph of a holomorphic correspondence on
$\Gamma $
is the graph of a holomorphic correspondence on
![]() $\widehat {\mathbb {C}}$
. Let
$\widehat {\mathbb {C}}$
. Let
![]() $g:\Omega \to \widehat {\mathbb {C}}$
be a holomorphic function defined on a domain
$g:\Omega \to \widehat {\mathbb {C}}$
be a holomorphic function defined on a domain
![]() $\Omega $
of
$\Omega $
of
![]() $\widehat {\mathbb {C}}$
, whose graph
$\widehat {\mathbb {C}}$
, whose graph
![]() $\operatorname {Gr}(g)$
is contained in one of the irreducible components
$\operatorname {Gr}(g)$
is contained in one of the irreducible components
![]() $\Gamma (i)$
of
$\Gamma (i)$
of
![]() $\Gamma $
. If
$\Gamma $
. If
![]() $a\in \Omega $
is a critical point for g, then
$a\in \Omega $
is a critical point for g, then
![]() $(a,g(a))\in A_2(\Gamma (i))\subset A_2(\Gamma )$
and therefore
$(a,g(a))\in A_2(\Gamma (i))\subset A_2(\Gamma )$
and therefore
![]() $g(a)\in B_2(\Gamma )$
, i.e., the critical value
$g(a)\in B_2(\Gamma )$
, i.e., the critical value
![]() of the function g is a critical value for the holomorphic correspondence associated to
of the function g is a critical value for the holomorphic correspondence associated to
![]() $\Gamma $
, as well.
$\Gamma $
, as well.
On the other hand, if
![]() $\alpha \notin A_1(\Gamma )$
, then there exists a holomorphic function
$\alpha \notin A_1(\Gamma )$
, then there exists a holomorphic function
![]() $g:\Omega \to \widehat {\mathbb {C}}$
defined on a neighborhood
$g:\Omega \to \widehat {\mathbb {C}}$
defined on a neighborhood
![]() $\Omega $
of
$\Omega $
of
![]() $a=\pi (\alpha )$
, such that
$a=\pi (\alpha )$
, such that
![]() $(a,g(a))=\alpha $
, and
$(a,g(a))=\alpha $
, and
![]() $\operatorname {Gr}(g)\subset \Gamma (i)$
for some i. If in addition
$\operatorname {Gr}(g)\subset \Gamma (i)$
for some i. If in addition
![]() $\alpha \in A_2(\Gamma )$
, then g is not locally injective at a, and therefore
$\alpha \in A_2(\Gamma )$
, then g is not locally injective at a, and therefore
![]() $g'(a)=0$
. Therefore, a is a critical point of g and
$g'(a)=0$
. Therefore, a is a critical point of g and
![]() $\pi _2(\alpha )=g(a)$
is a critical value of g.
$\pi _2(\alpha )=g(a)$
is a critical value of g.
If we denote by
![]() $\operatorname {CritPt}(g)$
the set of critical points of g, and by
$\operatorname {CritPt}(g)$
the set of critical points of g, and by
the set of critical values of g, then we get a motivation for the name ‘critical values’ in Definition 2.3 by the containment
 $$ \begin{align*}B_2(\Gamma)\setminus B_1(\Gamma)\subset\bigcup\limits_{i}\bigcup\limits_{\operatorname{Gr}(g)\subset\Gamma(i)}\operatorname{CritVal}(g),\end{align*} $$
$$ \begin{align*}B_2(\Gamma)\setminus B_1(\Gamma)\subset\bigcup\limits_{i}\bigcup\limits_{\operatorname{Gr}(g)\subset\Gamma(i)}\operatorname{CritVal}(g),\end{align*} $$
where the first union runs over the irreducible components of
![]() $\Gamma $
and the second union runs over all the holomorphic functions
$\Gamma $
and the second union runs over all the holomorphic functions
![]() $g:\Omega \to \widehat {\mathbb {C}}$
whose graph
$g:\Omega \to \widehat {\mathbb {C}}$
whose graph
![]() $\operatorname {Gr}(g)$
is contained in
$\operatorname {Gr}(g)$
is contained in
![]() $\Gamma (i)$
.
$\Gamma (i)$
.
Proposition 2.4. For every
![]() $a\in \mathbb {C}\setminus \lbrace 1\rbrace $
, we have that
$a\in \mathbb {C}\setminus \lbrace 1\rbrace $
, we have that
 $$ \begin{align} A_1(\Gamma_a)=\bigg\lbrace \bigg(\infty,\frac{a+1}{2}\bigg),\bigg( -2,1\bigg),\bigg(2,\frac{3a+1}{3+a}\bigg)\bigg\rbrace, \end{align} $$
$$ \begin{align} A_1(\Gamma_a)=\bigg\lbrace \bigg(\infty,\frac{a+1}{2}\bigg),\bigg( -2,1\bigg),\bigg(2,\frac{3a+1}{3+a}\bigg)\bigg\rbrace, \end{align} $$
and
 $$ \begin{align} A_2(\Gamma_a)=\bigg\lbrace \bigg(\infty,\frac{a+1}{2}\bigg),\bigg(1,\frac{4a+2}{a+5}\bigg), \bigg(-1,\frac{2}{3-a}\bigg)\bigg\rbrace. \end{align} $$
$$ \begin{align} A_2(\Gamma_a)=\bigg\lbrace \bigg(\infty,\frac{a+1}{2}\bigg),\bigg(1,\frac{4a+2}{a+5}\bigg), \bigg(-1,\frac{2}{3-a}\bigg)\bigg\rbrace. \end{align} $$
As a consequence,
![]() $B_1(\Gamma _a)=\lbrace \infty ,-2,2\rbrace $
and
$B_1(\Gamma _a)=\lbrace \infty ,-2,2\rbrace $
and
![]() $B_2(\Gamma _a)=\lbrace ({a+1})/{2},({4a+2})/({a+5}), {2}/({3-a})\rbrace $
. Moreover,
$B_2(\Gamma _a)=\lbrace ({a+1})/{2},({4a+2})/({a+5}), {2}/({3-a})\rbrace $
. Moreover,
![]() $\Gamma _a$
is smooth at all points except
$\Gamma _a$
is smooth at all points except
![]() $(\infty ,({a+1})/{2})$
.
$(\infty ,({a+1})/{2})$
.
To prove this proposition, we first prove the following lemma.
Lemma 2.5. For each
![]() $a\in \mathbb {C}\setminus \lbrace 1\rbrace $
,
$a\in \mathbb {C}\setminus \lbrace 1\rbrace $
,
and
Thus,
![]() $B_1(\Gamma _{\operatorname {Cov^Q_0}})=\lbrace \infty , -2,2\rbrace $
and
$B_1(\Gamma _{\operatorname {Cov^Q_0}})=\lbrace \infty , -2,2\rbrace $
and
![]() $B_2(\Gamma _{\operatorname {Cov^Q_0}})=\lbrace \infty , 1,-1\rbrace $
.
$B_2(\Gamma _{\operatorname {Cov^Q_0}})=\lbrace \infty , 1,-1\rbrace $
.
Proof. Differentiating the equation
![]() $P_Q(z,w)=0$
with respect to w, we get that
$P_Q(z,w)=0$
with respect to w, we get that
![]() $\partial _w P_Q(z,w)=z+2w$
vanishes if and only if
$\partial _w P_Q(z,w)=z+2w$
vanishes if and only if
![]() $w={-z}/{2}$
. Also,
$w={-z}/{2}$
. Also,
![]() $P_Q(z,-{z}/{2})=0$
if and only if
$P_Q(z,-{z}/{2})=0$
if and only if
![]() $z=\pm 2$
. Therefore,
$z=\pm 2$
. Therefore,
![]() ${dw}/{dz}$
exists on
${dw}/{dz}$
exists on
![]() $\mathbb {C}\setminus \lbrace -2, 2\rbrace $
. Thus, by the implicit function theorem, for every
$\mathbb {C}\setminus \lbrace -2, 2\rbrace $
. Thus, by the implicit function theorem, for every
![]() $(z,w)\in \Gamma _{\operatorname {Cov^Q_0}}$
such that
$(z,w)\in \Gamma _{\operatorname {Cov^Q_0}}$
such that
![]() $z\in \mathbb {C}\setminus \lbrace -2,2\rbrace $
, there exists a domain
$z\in \mathbb {C}\setminus \lbrace -2,2\rbrace $
, there exists a domain
![]() $\Omega $
containing z and a holomorphic function
$\Omega $
containing z and a holomorphic function
![]() $g:\Omega \to \widehat {\mathbb {C}}$
such that
$g:\Omega \to \widehat {\mathbb {C}}$
such that
![]() $g(z)=w$
and
$g(z)=w$
and
![]() $\operatorname {Gr}(g)=\Gamma _{\operatorname {Cov^Q_0}}\cap U$
, for some open neighborhood U of
$\operatorname {Gr}(g)=\Gamma _{\operatorname {Cov^Q_0}}\cap U$
, for some open neighborhood U of
![]() $(z,w)$
. In addition, the function g will be locally injective at z if
$(z,w)$
. In addition, the function g will be locally injective at z if
![]() $\partial _z P_Q(z,w)=2z+w$
is non-zero. Therefore, if
$\partial _z P_Q(z,w)=2z+w$
is non-zero. Therefore, if
![]() $(z,w)\in \Gamma _{\operatorname {Cov^Q_0}}$
satisfies that both z and w are different from
$(z,w)\in \Gamma _{\operatorname {Cov^Q_0}}$
satisfies that both z and w are different from
![]() $\pm 2$
, then
$\pm 2$
, then
![]() $(z,w)\notin A_2(\Gamma _{\operatorname {Cov^Q_0}})$
.
$(z,w)\notin A_2(\Gamma _{\operatorname {Cov^Q_0}})$
.
On the other hand, observe that the only points
![]() $(z,w)\in \Gamma _{\operatorname {Cov^Q_0}}$
with
$(z,w)\in \Gamma _{\operatorname {Cov^Q_0}}$
with
![]() $z=\pm 2$
are
$z=\pm 2$
are
![]() $(-2,1)$
and
$(-2,1)$
and
![]() $(2,-1)$
. In particular,
$(2,-1)$
. In particular,
![]() $w\neq \pm 2$
, and by the symmetry of the above argument, we can use the implicit function theorem to obtain a neighborhood U of w and a function
$w\neq \pm 2$
, and by the symmetry of the above argument, we can use the implicit function theorem to obtain a neighborhood U of w and a function
![]() $g:U\to \widehat {\mathbb {C}}$
satisfying
$g:U\to \widehat {\mathbb {C}}$
satisfying
![]() $\operatorname {Gr}(g)\subset \Gamma _{\operatorname {Cov^Q_0}}$
and
$\operatorname {Gr}(g)\subset \Gamma _{\operatorname {Cov^Q_0}}$
and
![]() $g(w)=z$
, and such that
$g(w)=z$
, and such that
![]() is injective in the neighborhood
is injective in the neighborhood
![]() $(g(U)\times U)\cap \Gamma _{\operatorname {Cov^Q_0}}$
of
$(g(U)\times U)\cap \Gamma _{\operatorname {Cov^Q_0}}$
of
![]() $(z,w)$
. This proves that neither
$(z,w)$
. This proves that neither
![]() $(-2,1)$
or
$(-2,1)$
or
![]() $(2,-1)$
belong to
$(2,-1)$
belong to
![]() $A_2(\Gamma _{\operatorname {Cov^Q_0}})$
. Since the only points
$A_2(\Gamma _{\operatorname {Cov^Q_0}})$
. Since the only points
![]() $(z,w)\in \Gamma _{\operatorname {Cov^Q_0}}$
with
$(z,w)\in \Gamma _{\operatorname {Cov^Q_0}}$
with
![]() $z=\pm 1$
are
$z=\pm 1$
are
![]() $(1,-2)$
and
$(1,-2)$
and
![]() $(-1,2)$
, and since
$(-1,2)$
, and since
![]() $\Gamma _{\operatorname {Cov^Q_0}}\setminus (\mathbb {C}\times \mathbb {C})=\lbrace (\infty ,\infty )\rbrace $
, we have that
$\Gamma _{\operatorname {Cov^Q_0}}\setminus (\mathbb {C}\times \mathbb {C})=\lbrace (\infty ,\infty )\rbrace $
, we have that
![]() $A_2(\Gamma _{\operatorname {Cov^Q_0}})$
is contained in
$A_2(\Gamma _{\operatorname {Cov^Q_0}})$
is contained in
![]() $\lbrace (\infty ,\infty ),(1,-2),(-1,2)\rbrace $
.
$\lbrace (\infty ,\infty ),(1,-2),(-1,2)\rbrace $
.
We will check that for every neighborhood W of
![]() $(\infty ,\infty )$
,
$(\infty ,\infty )$
,
![]() $(1,-2)$
, and
$(1,-2)$
, and
![]() $(-1,2)$
, we have that
$(-1,2)$
, we have that
![]() is not injective. Let
is not injective. Let
![]() $W_1,W_2$
, and
$W_1,W_2$
, and
![]() $W_3$
be open neighborhoods of
$W_3$
be open neighborhoods of
![]() $(\infty ,\infty )$
,
$(\infty ,\infty )$
,
![]() $(1,-2)$
, and
$(1,-2)$
, and
![]() $(-1,2)$
, respectively. Then there exists
$(-1,2)$
, respectively. Then there exists
![]() $T>0$
such that for every
$T>0$
such that for every
![]() $0<t<T$
,
$0<t<T$
,
 $$ \begin{align*}\bigg(\frac{1}{2}\bigg(\!\pm\sqrt{3}\sqrt{-\frac{1}{t^2}-\frac{4}{t}}+\frac{1}{t}+2\bigg),-2-\frac{1}{t}\bigg)\in\Gamma_{\operatorname{Cov^Q_0}}\cap W_1,\end{align*} $$
$$ \begin{align*}\bigg(\frac{1}{2}\bigg(\!\pm\sqrt{3}\sqrt{-\frac{1}{t^2}-\frac{4}{t}}+\frac{1}{t}+2\bigg),-2-\frac{1}{t}\bigg)\in\Gamma_{\operatorname{Cov^Q_0}}\cap W_1,\end{align*} $$
 $$ \begin{align*}\bigg(\frac{1}{2}\big(\!\pm\sqrt{3}\sqrt{-t^2-4t}+t+2\big),-2-t\bigg)\in\Gamma_{\operatorname{Cov^Q_0}}\cap W_2,\end{align*} $$
$$ \begin{align*}\bigg(\frac{1}{2}\big(\!\pm\sqrt{3}\sqrt{-t^2-4t}+t+2\big),-2-t\bigg)\in\Gamma_{\operatorname{Cov^Q_0}}\cap W_2,\end{align*} $$
and
 $$ \begin{align*}\bigg(\frac{1}{2}\big(\!\pm\sqrt{3}\sqrt{4t-t^2}+t-2\big),2-t\bigg)\in\Gamma_{\operatorname{Cov^Q_0}}\cap W_3.\end{align*} $$
$$ \begin{align*}\bigg(\frac{1}{2}\big(\!\pm\sqrt{3}\sqrt{4t-t^2}+t-2\big),2-t\bigg)\in\Gamma_{\operatorname{Cov^Q_0}}\cap W_3.\end{align*} $$
We conclude that
![]() $A_2(\Gamma _{\operatorname {Cov^Q_0}})=\lbrace (\infty ,\infty ),(1,-2),(-1,2)\rbrace $
, and by the symmetry of
$A_2(\Gamma _{\operatorname {Cov^Q_0}})=\lbrace (\infty ,\infty ),(1,-2),(-1,2)\rbrace $
, and by the symmetry of
![]() $\operatorname {Cov^Q_0}$
,
$\operatorname {Cov^Q_0}$
,
![]() $A_1(\Gamma _{\operatorname {Cov^Q_0}})=\lbrace (\infty ,\infty ),(-2,1),(2,-1)\rbrace $
. We conclude that
$A_1(\Gamma _{\operatorname {Cov^Q_0}})=\lbrace (\infty ,\infty ),(-2,1),(2,-1)\rbrace $
. We conclude that
Proof of Proposition 2.4.
Since
![]() $\mathcal {F}_a=\operatorname {J}_a\circ \operatorname {Cov^Q_0}$
and
$\mathcal {F}_a=\operatorname {J}_a\circ \operatorname {Cov^Q_0}$
and
![]() $\operatorname {J}_a$
is an involution, we have that
$\operatorname {J}_a$
is an involution, we have that
for
![]() $j=1,2$
. Using Lemma 2.5, this gives us equations (3) and (4), and thus
$j=1,2$
. Using Lemma 2.5, this gives us equations (3) and (4), and thus
![]() $B_1(\Gamma _a)=\lbrace \infty , -2,2\rbrace $
and
$B_1(\Gamma _a)=\lbrace \infty , -2,2\rbrace $
and
 $$ \begin{align*}B_2(\Gamma_a)=\lbrace \operatorname{J}_a(\infty),\operatorname{J}_a(-2),\operatorname{J}_a(2)\rbrace=\bigg\lbrace \frac{a+1}{2},\frac{4a+2}{a+5},\frac{2}{3-a}\bigg\rbrace.\end{align*} $$
$$ \begin{align*}B_2(\Gamma_a)=\lbrace \operatorname{J}_a(\infty),\operatorname{J}_a(-2),\operatorname{J}_a(2)\rbrace=\bigg\lbrace \frac{a+1}{2},\frac{4a+2}{a+5},\frac{2}{3-a}\bigg\rbrace.\end{align*} $$
In addition, observe that locally,
![]() $\Gamma _a$
is either a function on z or on w for all
$\Gamma _a$
is either a function on z or on w for all
![]() $(z,w)\in \Gamma _a$
with
$(z,w)\in \Gamma _a$
with
![]() $z\neq \infty $
, then the only point that can be irregular is
$z\neq \infty $
, then the only point that can be irregular is
![]() $(\infty ,({a+1})/{2})$
. Indeed, this point is irregular, as the curve given by the points
$(\infty ,({a+1})/{2})$
. Indeed, this point is irregular, as the curve given by the points
 $$ \begin{align*}\bigg(\frac{1}{2}\bigg(\pm\sqrt{3}\sqrt{-\frac{1}{t^2}-\frac{4}{t}}+\frac{1}{t}+2\bigg),-2-\frac{1}{t}\bigg)\in\Gamma_{\operatorname{Cov^Q_0}}\end{align*} $$
$$ \begin{align*}\bigg(\frac{1}{2}\bigg(\pm\sqrt{3}\sqrt{-\frac{1}{t^2}-\frac{4}{t}}+\frac{1}{t}+2\bigg),-2-\frac{1}{t}\bigg)\in\Gamma_{\operatorname{Cov^Q_0}}\end{align*} $$
self-intersects at
![]() $(\infty ,\infty )$
with an angle of
$(\infty ,\infty )$
with an angle of
![]() ${2\pi }/{3}$
. In other words, there are two functions
${2\pi }/{3}$
. In other words, there are two functions
![]() $z(w)$
which intersect with different derivatives, which makes
$z(w)$
which intersect with different derivatives, which makes
![]() $(\infty ,\infty )$
an irregular point of
$(\infty ,\infty )$
an irregular point of
![]() $\Gamma _{\operatorname {Cov^Q_0}}$
. Thus, passing through the involution
$\Gamma _{\operatorname {Cov^Q_0}}$
. Thus, passing through the involution
![]() $\operatorname {J}_a$
, we get that
$\operatorname {J}_a$
, we get that
![]() $(\infty ,({a+1})/{2})$
is an irregular point of
$(\infty ,({a+1})/{2})$
is an irregular point of
![]() $\Gamma _a$
.
$\Gamma _a$
.
Remark 2.6. The correspondence
![]() $\operatorname {Cov^Q_0}$
, and hence
$\operatorname {Cov^Q_0}$
, and hence
![]() $\mathcal {F}_a$
, sends open sets to open sets. Indeed, let
$\mathcal {F}_a$
, sends open sets to open sets. Indeed, let
![]() $U\subset \widehat {\mathbb {C}}$
be open and take
$U\subset \widehat {\mathbb {C}}$
be open and take
![]() $w_0\in \operatorname {Cov^Q_0}(U)$
. Then there exists
$w_0\in \operatorname {Cov^Q_0}(U)$
. Then there exists
![]() $z_0\in U$
for which
$z_0\in U$
for which
![]() $(z_0,w_0)\in \Gamma _{\operatorname {Cov^Q_0}}$
. We will prove that
$(z_0,w_0)\in \Gamma _{\operatorname {Cov^Q_0}}$
. We will prove that
![]() $\operatorname {Cov^Q_0}(U)$
is open by showing that in all the cases,
$\operatorname {Cov^Q_0}(U)$
is open by showing that in all the cases,
![]() $w_0\in \operatorname {int}(\operatorname {Cov^Q_0}(U))$
.
$w_0\in \operatorname {int}(\operatorname {Cov^Q_0}(U))$
.
-
• Suppose
 $(z_0,w_0)\notin A_1(\Gamma _{\operatorname {Cov^Q_0}})$
. By Lemma 2.5 and since
$(z_0,w_0)\notin A_1(\Gamma _{\operatorname {Cov^Q_0}})$
. By Lemma 2.5 and since
 $(\operatorname {Cov^Q_0})^{-1}(\infty )=\lbrace \infty \rbrace $
, we have that
$(\operatorname {Cov^Q_0})^{-1}(\infty )=\lbrace \infty \rbrace $
, we have that
 $w_0\neq \infty $
. Moreover, there exists a holomorphic function
$w_0\neq \infty $
. Moreover, there exists a holomorphic function
 $g:\Omega \to \mathbb {C}$
on an open subset
$g:\Omega \to \mathbb {C}$
on an open subset
 $\Omega \subset U$
, and
$\Omega \subset U$
, and
 $(z_0,w_0)\in \operatorname {Gr}(g)\subset \Gamma _{\operatorname {Cov^Q_0}}$
. Furthermore,
$(z_0,w_0)\in \operatorname {Gr}(g)\subset \Gamma _{\operatorname {Cov^Q_0}}$
. Furthermore,
 $\Gamma _{\operatorname {Cov^Q_0}}$
is irreducible and
$\Gamma _{\operatorname {Cov^Q_0}}$
is irreducible and
 $\operatorname {Cov^Q_0}$
is not constant, so g is not constant. Thus, g is open and then
$\operatorname {Cov^Q_0}$
is not constant, so g is not constant. Thus, g is open and then
 $w_0\in g(\Omega )\subset \operatorname {int}(\operatorname {Cov^Q_0}(U))$
.
$w_0\in g(\Omega )\subset \operatorname {int}(\operatorname {Cov^Q_0}(U))$
. -
• Now suppose
 $(z_0,w_0)\notin A_2(\Gamma _{\operatorname {Cov^Q_0}})$
. By Lemma 2.5 and since
$(z_0,w_0)\notin A_2(\Gamma _{\operatorname {Cov^Q_0}})$
. By Lemma 2.5 and since
 $\operatorname {Cov^Q_0}(\infty )=\lbrace \infty \rbrace $
, then
$\operatorname {Cov^Q_0}(\infty )=\lbrace \infty \rbrace $
, then
 $z_0\neq \infty $
and there exists a holomorphic function
$z_0\neq \infty $
and there exists a holomorphic function
 $\tilde {g}:\widetilde {\Omega }\to \mathbb {C}$
on an open subset
$\tilde {g}:\widetilde {\Omega }\to \mathbb {C}$
on an open subset
 $\widetilde {\Omega }\subset \mathbb {C}$
so that
$\widetilde {\Omega }\subset \mathbb {C}$
so that
 $(z_0,w_0)\in \iota (\operatorname {Gr}(\tilde {g}))\subset \Gamma _{\operatorname {Cov^Q_0}}$
. Since
$(z_0,w_0)\in \iota (\operatorname {Gr}(\tilde {g}))\subset \Gamma _{\operatorname {Cov^Q_0}}$
. Since
 $\tilde {g}$
is continuous, then
$\tilde {g}$
is continuous, then
 $\tilde {g}^{-1}(U)$
is open and
$\tilde {g}^{-1}(U)$
is open and
 $w_0\in \tilde {g}^{-1}(U)\subset \operatorname {int}(\operatorname {Cov^Q_0}(U))$
.
$w_0\in \tilde {g}^{-1}(U)\subset \operatorname {int}(\operatorname {Cov^Q_0}(U))$
. -
• Finally, if
 $(z_0,w_0)\in A_1(\Gamma _{\operatorname {Cov^Q_0}})\cap A_2(\Gamma _{\operatorname {Cov^Q_0}})$
, then Lemma 2.5 implies that
$(z_0,w_0)\in A_1(\Gamma _{\operatorname {Cov^Q_0}})\cap A_2(\Gamma _{\operatorname {Cov^Q_0}})$
, then Lemma 2.5 implies that
 $(z_0,w_0)=(\infty ,\infty )$
. For each
$(z_0,w_0)=(\infty ,\infty )$
. For each
 $r>0$
, put
$r>0$
, put
 . To show that
. To show that
 $\infty \in \operatorname {int}(\operatorname {Cov^Q_0}(U))$
, we will show that for every
$\infty \in \operatorname {int}(\operatorname {Cov^Q_0}(U))$
, we will show that for every
 $R>\sqrt {3}$
,
$R>\sqrt {3}$
,
 $U_{2R}\subset \operatorname {Cov^Q_0}(U_R)$
. We proceed by the contrapositive. If
$U_{2R}\subset \operatorname {Cov^Q_0}(U_R)$
. We proceed by the contrapositive. If
 $P_Q(z,w)=0$
and
$P_Q(z,w)=0$
and
 $|w|\leq R$
, then Hence,
$|w|\leq R$
, then Hence, $$ \begin{align*} |z|^2=|3-zw-w^2|\leq 3+|z||w|+|w|^2\leq 2R^2+|z|R. \end{align*} $$
$$ \begin{align*} |z|^2=|3-zw-w^2|\leq 3+|z||w|+|w|^2\leq 2R^2+|z|R. \end{align*} $$
 $|z|^2-R|z|-2R^2\leq 0$
and
$|z|^2-R|z|-2R^2\leq 0$
and
 $|z|\leq 2R$
. This implies that for every
$|z|\leq 2R$
. This implies that for every
 $R>\sqrt {3}$
, we have that
$R>\sqrt {3}$
, we have that
 $\operatorname {Cov^Q_0}(U_{2R})\subset U_R$
. By the symmetry of
$\operatorname {Cov^Q_0}(U_{2R})\subset U_R$
. By the symmetry of
 $\operatorname {Cov^Q_0}$
, Moreover, if
$\operatorname {Cov^Q_0}$
, Moreover, if $$ \begin{align*}U_{2R}\subset\operatorname{Cov^Q_0}(\operatorname{Cov^Q_0}(U_{2R}))\subset\operatorname{Cov^Q_0}(U_R).\end{align*} $$
$$ \begin{align*}U_{2R}\subset\operatorname{Cov^Q_0}(\operatorname{Cov^Q_0}(U_{2R}))\subset\operatorname{Cov^Q_0}(U_R).\end{align*} $$
 $R>\sqrt {3}$
is large enough so that
$R>\sqrt {3}$
is large enough so that
 $U_R\subset U$
, then
$U_R\subset U$
, then  $$ \begin{align*} \infty\in U_{2R}\subset \operatorname{int}(\operatorname{Cov^Q_0}(U)).\end{align*} $$
$$ \begin{align*} \infty\in U_{2R}\subset \operatorname{int}(\operatorname{Cov^Q_0}(U)).\end{align*} $$
Therefore,
![]() $\operatorname {Cov^Q_0}$
sends open sets to open sets. Since the involution
$\operatorname {Cov^Q_0}$
sends open sets to open sets. Since the involution
![]() $\operatorname {J}_a$
also sends open sets to open sets, then so does
$\operatorname {J}_a$
also sends open sets to open sets, then so does
![]() $\mathcal {F}_a$
.
$\mathcal {F}_a$
.
2.4 Klein combination pairs
In this section, we will define the set
![]() $\mathcal {K}$
of parameters we will consider for our family.
$\mathcal {K}$
of parameters we will consider for our family.
Definition 2.7. A fundamental domain for an irreducible holomorphic correspondence F is an open set
![]() $\Delta _F$
that is maximal with the property that
$\Delta _F$
that is maximal with the property that
![]() $\Delta _F\cap F(\Delta _F)=\emptyset $
.
$\Delta _F\cap F(\Delta _F)=\emptyset $
.
Definition 2.8. We say that a pair
![]() $(\Delta _{\operatorname {Cov^Q_0}},\Delta _{\operatorname {J}_a})$
of fundamental domains for
$(\Delta _{\operatorname {Cov^Q_0}},\Delta _{\operatorname {J}_a})$
of fundamental domains for
![]() $\operatorname {Cov^Q_0}$
and
$\operatorname {Cov^Q_0}$
and
![]() $\operatorname {J}_a$
, respectively, is a Klein combination pair for
$\operatorname {J}_a$
, respectively, is a Klein combination pair for
![]() $\mathcal {F}_a$
if both
$\mathcal {F}_a$
if both
![]() $\Delta _{\operatorname {Cov^Q_0}}$
and
$\Delta _{\operatorname {Cov^Q_0}}$
and
![]() $\Delta _{\operatorname {J}_a}$
are simply connected domains, bounded by Jordan curves, and satisfy
$\Delta _{\operatorname {J}_a}$
are simply connected domains, bounded by Jordan curves, and satisfy
We define as well the Klein combination locus
![]() $\mathcal {K}$
to be the set of parameters
$\mathcal {K}$
to be the set of parameters
![]() $a\in \mathbb {C}\setminus \lbrace 1\rbrace $
for which there exist a Klein combination pair.
$a\in \mathbb {C}\setminus \lbrace 1\rbrace $
for which there exist a Klein combination pair.
In [Reference Bullett and Lomonaco4], for
![]() $|a-4|\leq 3$
,
$|a-4|\leq 3$
,
![]() $a\neq 1$
, the authors found a Klein combination pair for
$a\neq 1$
, the authors found a Klein combination pair for
![]() $\mathcal {F}_a$
, where
$\mathcal {F}_a$
, where
![]() $\Delta _{\operatorname {Cov^Q_0}}$
is given by the right side of the curve
$\Delta _{\operatorname {Cov^Q_0}}$
is given by the right side of the curve

and
![]() $\Delta _{\operatorname {J}_a}$
is given by the exterior of the circle passing through
$\Delta _{\operatorname {J}_a}$
is given by the exterior of the circle passing through
![]() $z=1$
and
$z=1$
and
![]() $z=a$
with diameter contained in the real line.
$z=a$
with diameter contained in the real line.
This pair
![]() $(\Delta _{\operatorname {Cov^Q_0}},\Delta _{\operatorname {J}_a})$
is composed by simply connected fundamental domains for
$(\Delta _{\operatorname {Cov^Q_0}},\Delta _{\operatorname {J}_a})$
is composed by simply connected fundamental domains for
![]() $\operatorname {Cov^Q_0}$
and
$\operatorname {Cov^Q_0}$
and
![]() $\operatorname {J}_a$
, respectively, whose boundaries are Jordan curves, smooth except from
$\operatorname {J}_a$
, respectively, whose boundaries are Jordan curves, smooth except from
![]() $\partial \Delta _{\operatorname {Cov^Q_0}}$
at
$\partial \Delta _{\operatorname {Cov^Q_0}}$
at
![]() $(\infty ,\infty )$
(see Figure 1 and [Reference Bullett and Lomonaco4, Proposition 3.3]). In particular,
$(\infty ,\infty )$
(see Figure 1 and [Reference Bullett and Lomonaco4, Proposition 3.3]). In particular,

Figure 1 Klein combination pair for
![]() $|a-4|\leq 3$
.
$|a-4|\leq 3$
.
From now on, whenever
![]() $a\in \mathcal {K}$
, we denote by
$a\in \mathcal {K}$
, we denote by
![]() $(\Delta _{\operatorname {Cov^Q_0}},\Delta _{\operatorname {J}_a})$
a Klein combination pair for
$(\Delta _{\operatorname {Cov^Q_0}},\Delta _{\operatorname {J}_a})$
a Klein combination pair for
![]() $\mathcal {F}_a$
.
$\mathcal {F}_a$
.
The following remark will be useful to prove that
![]() $\mathcal {F}_a$
is not modular, and later to analyze the asymptotic behavior of
$\mathcal {F}_a$
is not modular, and later to analyze the asymptotic behavior of
![]() $\mathcal {F}_a$
.
$\mathcal {F}_a$
.
Remark 2.9. Let
![]() $a\in \mathcal {K}$
.
$a\in \mathcal {K}$
.
-
(1) Note that
 $\mathcal {F}_a(\widehat {\mathbb {C}}\setminus \Delta _{\operatorname {J}_a})\subset \widehat {\mathbb {C}}\setminus \Delta _{\operatorname {J}_a}$
and
$\mathcal {F}_a(\widehat {\mathbb {C}}\setminus \Delta _{\operatorname {J}_a})\subset \widehat {\mathbb {C}}\setminus \Delta _{\operatorname {J}_a}$
and
 ${\mathcal {F}_a((\widehat {\mathbb {C}}\setminus \Delta _{\operatorname {J}_a})\setminus \lbrace 1\rbrace )\subset \widehat {\mathbb {C}}\setminus \overline {\Delta _{\operatorname {J}_a}}}$
. Indeed,
${\mathcal {F}_a((\widehat {\mathbb {C}}\setminus \Delta _{\operatorname {J}_a})\setminus \lbrace 1\rbrace )\subset \widehat {\mathbb {C}}\setminus \overline {\Delta _{\operatorname {J}_a}}}$
. Indeed,  $$ \begin{align*}\mathcal{F}_a(1)=\operatorname{J}_a(\operatorname{Cov^Q_0} (1))=\operatorname{J}_a(\lbrace 1,-2\rbrace)=\bigg\lbrace 1,\frac{4a+2}{a+5}\bigg\rbrace.\end{align*} $$
$$ \begin{align*}\mathcal{F}_a(1)=\operatorname{J}_a(\operatorname{Cov^Q_0} (1))=\operatorname{J}_a(\lbrace 1,-2\rbrace)=\bigg\lbrace 1,\frac{4a+2}{a+5}\bigg\rbrace.\end{align*} $$
From Remark 2.6, we have that
 $\operatorname {Cov^Q_0}$
sends open sets to open sets. In particular,
$\operatorname {Cov^Q_0}$
sends open sets to open sets. In particular,
 $-$
2 cannot belong to
$-$
2 cannot belong to
 $\Delta _{\operatorname {Cov^Q_0}}$
, as
$\Delta _{\operatorname {Cov^Q_0}}$
, as
 $1\notin \operatorname {Cov^Q_0}(\Delta _{\operatorname {Cov^Q_0}})=\widehat {\mathbb {C}}\setminus \overline {\Delta _{\operatorname {Cov^Q_0}}}$
. By the Klein combination pair condition, this implies that
$1\notin \operatorname {Cov^Q_0}(\Delta _{\operatorname {Cov^Q_0}})=\widehat {\mathbb {C}}\setminus \overline {\Delta _{\operatorname {Cov^Q_0}}}$
. By the Klein combination pair condition, this implies that
 $-2\in \Delta _{\operatorname {J}_a}$
, and thus
$-2\in \Delta _{\operatorname {J}_a}$
, and thus
 $\operatorname {J}_a(-2)=({4a+2})/({a+5})\notin \Delta _{\operatorname {J}_a}$
. Since we also have that
$\operatorname {J}_a(-2)=({4a+2})/({a+5})\notin \Delta _{\operatorname {J}_a}$
. Since we also have that
 $1\notin \Delta _{\operatorname {J}_a}$
, we have that
$1\notin \Delta _{\operatorname {J}_a}$
, we have that  $$ \begin{align*}\mathcal{F}_a(1)\subset\widehat{\mathbb{C}}\setminus\Delta_{\operatorname{J}_a}.\end{align*} $$
$$ \begin{align*}\mathcal{F}_a(1)\subset\widehat{\mathbb{C}}\setminus\Delta_{\operatorname{J}_a}.\end{align*} $$
However, for
 $z\in \widehat {\mathbb {C}}\setminus \Delta _{\operatorname {J}_a}$
,
$z\in \widehat {\mathbb {C}}\setminus \Delta _{\operatorname {J}_a}$
,
 $z\neq 1$
, we have that
$z\neq 1$
, we have that
 $z\in \Delta _{\operatorname {Cov^Q_0}}$
. Therefore,
$z\in \Delta _{\operatorname {Cov^Q_0}}$
. Therefore,  $$ \begin{align*}\operatorname{Cov^Q_0}(z)\subset\widehat{\mathbb{C}}\setminus\overline{\Delta_{\operatorname{Cov^Q_0}}}\subset\Delta_{\operatorname{J}_a},\end{align*} $$
$$ \begin{align*}\operatorname{Cov^Q_0}(z)\subset\widehat{\mathbb{C}}\setminus\overline{\Delta_{\operatorname{Cov^Q_0}}}\subset\Delta_{\operatorname{J}_a},\end{align*} $$
and thus, since
 $\operatorname {J}_a$
is an involution fixing
$\operatorname {J}_a$
is an involution fixing
 $\partial \Delta _{\operatorname {J}_a}$
,
$\partial \Delta _{\operatorname {J}_a}$
,  $$ \begin{align*}\mathcal{F}_a(z)=\operatorname{J}_a\circ\operatorname{Cov^Q_0}(z)\subset\operatorname{J}_a(\Delta_{\operatorname{J}_a})=\widehat{\mathbb{C}}\setminus\overline{\Delta_{\operatorname{J}_a}}.\end{align*} $$
$$ \begin{align*}\mathcal{F}_a(z)=\operatorname{J}_a\circ\operatorname{Cov^Q_0}(z)\subset\operatorname{J}_a(\Delta_{\operatorname{J}_a})=\widehat{\mathbb{C}}\setminus\overline{\Delta_{\operatorname{J}_a}}.\end{align*} $$
In particular,
 $\Delta _{\operatorname {J}_a}\setminus \mathcal {F}_a(\widehat {\mathbb {C}}\setminus \Delta _{\operatorname {J}_a})\neq \emptyset $
.
$\Delta _{\operatorname {J}_a}\setminus \mathcal {F}_a(\widehat {\mathbb {C}}\setminus \Delta _{\operatorname {J}_a})\neq \emptyset $
. -
(2) Observe that
 $\mathcal {F}_a^{-1}(\Delta _{\operatorname {J}_a})\subset \Delta _{\operatorname {J}_a}$
and
$\mathcal {F}_a^{-1}(\Delta _{\operatorname {J}_a})\subset \Delta _{\operatorname {J}_a}$
and
 $\mathcal {F}_a^{-1}(\overline {\Delta _{\operatorname {J}_a}})\subset \Delta _{\operatorname {J}_a}\cup \lbrace 1\rbrace $
. Indeed, for every
$\mathcal {F}_a^{-1}(\overline {\Delta _{\operatorname {J}_a}})\subset \Delta _{\operatorname {J}_a}\cup \lbrace 1\rbrace $
. Indeed, for every
 $z\in \Delta _{\operatorname {J}_a}$
, we have that
$z\in \Delta _{\operatorname {J}_a}$
, we have that
 $\operatorname {J}_a(z)\in \widehat {\mathbb {C}}\setminus \overline {\Delta _{\operatorname {J}_a}}\subset \Delta _{\operatorname {Cov^Q_0}}$
. From Remark 2.6 and since
$\operatorname {J}_a(z)\in \widehat {\mathbb {C}}\setminus \overline {\Delta _{\operatorname {J}_a}}\subset \Delta _{\operatorname {Cov^Q_0}}$
. From Remark 2.6 and since
 $(\Delta_{\operatorname {Cov^Q_0}},\Delta _{\operatorname {J}_a})$
is a Klein combination pair, then
$(\Delta_{\operatorname {Cov^Q_0}},\Delta _{\operatorname {J}_a})$
is a Klein combination pair, then  $$ \begin{align*}\mathcal{F}_a^{-1}(z)=\operatorname{Cov^Q_0}(\widehat{\mathbb{C}}\setminus\overline{\Delta_{\operatorname{J}_a}})\subset\operatorname{Cov^Q_0}(\Delta_{\operatorname{Cov^Q_0}})\subset\widehat{\mathbb{C}}\setminus\overline{\Delta_{\operatorname{Cov^Q_0}}}\subset\Delta_{\operatorname{J}_a}.\end{align*} $$
$$ \begin{align*}\mathcal{F}_a^{-1}(z)=\operatorname{Cov^Q_0}(\widehat{\mathbb{C}}\setminus\overline{\Delta_{\operatorname{J}_a}})\subset\operatorname{Cov^Q_0}(\Delta_{\operatorname{Cov^Q_0}})\subset\widehat{\mathbb{C}}\setminus\overline{\Delta_{\operatorname{Cov^Q_0}}}\subset\Delta_{\operatorname{J}_a}.\end{align*} $$
Furthermore, for
 $w\in \overline {\Delta _{\operatorname {J}_a}}$
, we have that
$w\in \overline {\Delta _{\operatorname {J}_a}}$
, we have that 
3 Clasification of the family
 $\lbrace \mathcal {F}_a\rbrace _a$
$\lbrace \mathcal {F}_a\rbrace _a$
In this section, we prove that
![]() $\mathcal {F}_a$
is weakly modular but not modular, for every
$\mathcal {F}_a$
is weakly modular but not modular, for every
![]() $a\in \mathcal {K}$
. In addition, we prove that it does not satisfy the required conditions for the equidistribution result [Reference Bharali and Sridharan1, Theorem 3.5]. All together proving Theorem 1.1.
$a\in \mathcal {K}$
. In addition, we prove that it does not satisfy the required conditions for the equidistribution result [Reference Bharali and Sridharan1, Theorem 3.5]. All together proving Theorem 1.1.
3.1 Modularity and weak modularity
Definition 3.1. Let G be a connected Lie group,
![]() $\Lambda $
a torsion free lattice, and K a compact Lie subgroup. Let
$\Lambda $
a torsion free lattice, and K a compact Lie subgroup. Let
![]() $g\in G$
be such that
$g\in G$
be such that
![]() $g\Lambda g^{-1}\cap \Lambda $
has finite index in
$g\Lambda g^{-1}\cap \Lambda $
has finite index in
![]() $\Lambda $
. The irreducible modular correspondence induced by g is the multivalued map
$\Lambda $
. The irreducible modular correspondence induced by g is the multivalued map
![]() $F_g$
on
$F_g$
on
![]() $X=\Lambda \setminus G/K$
corresponding to the projection to X of the map
$X=\Lambda \setminus G/K$
corresponding to the projection to X of the map
![]() $x\mapsto (x,gx)$
on
$x\mapsto (x,gx)$
on
![]() $G\to G\times G$
. Denote by
$G\to G\times G$
. Denote by
![]() $\Gamma _g$
the graph of
$\Gamma _g$
the graph of
![]() $F_g$
. A modular correspondence F is a correspondence whose graph is of the form
$F_g$
. A modular correspondence F is a correspondence whose graph is of the form
![]() $\sum _jn_j\Gamma _{g_j}$
, for
$\sum _jn_j\Gamma _{g_j}$
, for
![]() $\Gamma _{g_j}$
as before.
$\Gamma _{g_j}$
as before.
The following definition was introduced by Dinh, Kaufmann, and Wu in [Reference Dinh, Kaufmann and Wu15].
Definition 3.2. Let X be a compact Riemann surface and let F be a holomorphic correspondence on X with graph
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $d(F)=d(F^{-1})$
. We say that F is a weakly modular correspondence if there exist Borel probability measures
$d(F)=d(F^{-1})$
. We say that F is a weakly modular correspondence if there exist Borel probability measures
![]() $\mu _1$
and
$\mu _1$
and
![]() $\mu _2$
on X, such that
$\mu _2$
on X, such that
Remark 3.3
-
(1) Let F be a modular correspondence that is also a holomorphic correspondence. Then it is always the case that
 $$ \begin{align*} d(F)=\sum_j n_j[\Lambda: g_j\Lambda g_j^{-1}\cap\Lambda]=\sum_j n_j[\Lambda:g_j^{-1}\Lambda g_j\cap\Lambda]=d(F^{-1}). \end{align*} $$
$$ \begin{align*} d(F)=\sum_j n_j[\Lambda: g_j\Lambda g_j^{-1}\cap\Lambda]=\sum_j n_j[\Lambda:g_j^{-1}\Lambda g_j\cap\Lambda]=d(F^{-1}). \end{align*} $$
-
(2) With the notation in Definition 3.1, let
 $\unicode{x3bb} $
be the direct image on X of the finite Haar measure on
$\unicode{x3bb} $
be the direct image on X of the finite Haar measure on
 $\Lambda \setminus G$
. Then,
$\Lambda \setminus G$
. Then,
 $(1/d){(F_g)}F_g^*\unicode{x3bb} =\unicode{x3bb} $
and if we put
$(1/d){(F_g)}F_g^*\unicode{x3bb} =\unicode{x3bb} $
and if we put
 $\mu _1=\mu _2=\unicode{x3bb} $
, we get that
$\mu _1=\mu _2=\unicode{x3bb} $
, we get that 
Therefore, modular correspondences are weakly modular.
-
(3) The measure
 $\unicode{x3bb} $
above is Borel, invariant under
$\unicode{x3bb} $
above is Borel, invariant under
 $F_g$
, and assigns positive measure to non-empty open sets.
$F_g$
, and assigns positive measure to non-empty open sets.
Proof of Theorem 1.1 part 1.
Observe that the graph
![]() $\Gamma _{\operatorname {Cov^Q_0}}$
of the correspondence
$\Gamma _{\operatorname {Cov^Q_0}}$
of the correspondence
![]() $\operatorname {Cov^Q_0}$
is symmetric with respect to the diagonal
$\operatorname {Cov^Q_0}$
is symmetric with respect to the diagonal
![]() $\mathfrak {D}_{\widehat {\mathbb {C}}}=\lbrace (z,z) | z\in \widehat {\mathbb {C}}\rbrace $
, as
$\mathfrak {D}_{\widehat {\mathbb {C}}}=\lbrace (z,z) | z\in \widehat {\mathbb {C}}\rbrace $
, as
![]() $z\in \operatorname {Cov^Q_0}(w)$
if and only if
$z\in \operatorname {Cov^Q_0}(w)$
if and only if
![]() $w\in \operatorname {Cov^Q_0}(z)$
. Let m be any positive and finite measure on
$w\in \operatorname {Cov^Q_0}(z)$
. Let m be any positive and finite measure on
![]() $\Gamma _{\operatorname {Cov^Q_0}}$
, and
$\Gamma _{\operatorname {Cov^Q_0}}$
, and
![]() $\iota :\Gamma _{\operatorname {Cov^Q_0}}\to \Gamma _{\operatorname {Cov^Q_0}}$
the involution
$\iota :\Gamma _{\operatorname {Cov^Q_0}}\to \Gamma _{\operatorname {Cov^Q_0}}$
the involution
. Take
The measure
![]() $m_0$
is symmetric in
$m_0$
is symmetric in
![]() $\Gamma _{\operatorname {Cov^Q_0}}$
in the sense that
$\Gamma _{\operatorname {Cov^Q_0}}$
in the sense that
![]() $\iota ^*m'=m'$
and moreover
$\iota ^*m'=m'$
and moreover
After normalizing if necessary, this proves that
![]() $\operatorname {Cov^Q_0}$
is weakly modular with measures
$\operatorname {Cov^Q_0}$
is weakly modular with measures
and
. Our goal is to show there are probability measures
![]() $\mu _1$
and
$\mu _1$
and
![]() $\mu _2$
on
$\mu _2$
on
![]() $\widehat {\mathbb {C}}$
such that
$\widehat {\mathbb {C}}$
such that
where
![]() $\Gamma _a$
is the graph of the correspondence
$\Gamma _a$
is the graph of the correspondence
![]() $\mathcal {F}_a=\mathcal {F}_a\circ \operatorname {Cov^Q_0}$
.
$\mathcal {F}_a=\mathcal {F}_a\circ \operatorname {Cov^Q_0}$
.
Put
![]() and observe that by symmetry of
and observe that by symmetry of
![]() $\operatorname {J}_a$
, we have that
$\operatorname {J}_a$
, we have that
Now let
![]() $\widehat {\operatorname {J}_a}:\widehat {\mathbb {C}}\times \widehat {\mathbb {C}}\to \widehat {\mathbb {C}}\times \widehat {\mathbb {C}}$
be given by
$\widehat {\operatorname {J}_a}:\widehat {\mathbb {C}}\times \widehat {\mathbb {C}}\to \widehat {\mathbb {C}}\times \widehat {\mathbb {C}}$
be given by
![]() . Observe that whenever
. Observe that whenever
![]() $(z,w)\in \Gamma _{\operatorname {Cov^Q_0}}$
, then
$(z,w)\in \Gamma _{\operatorname {Cov^Q_0}}$
, then
![]() $(z,\operatorname {J}_a(w))\in \Gamma _a$
and
$(z,\operatorname {J}_a(w))\in \Gamma _a$
and
On the other hand,
![]() with multiplicity
with multiplicity
![]() $2$
. This, together with equations (5), (7), and (8) yield
$2$
. This, together with equations (5), (7), and (8) yield
Observe that
![]() and
and
![]() $\mu _2$
both have
$\mu _2$
both have
![]() $2$
times the mass of
$2$
times the mass of
![]() $\mu _1$
and
$\mu _1$
and
![]() $\mu _2$
. After normalizing, equation (9) proves that
$\mu _2$
. After normalizing, equation (9) proves that
![]() $\mathcal {F}_a$
is weakly modular, as desired.
$\mathcal {F}_a$
is weakly modular, as desired.
To check
![]() $\mathcal {F}_a$
is not modular, we will prove that no Borel measure
$\mathcal {F}_a$
is not modular, we will prove that no Borel measure
![]() $\unicode{x3bb} $
on
$\unicode{x3bb} $
on
![]() $\widehat {\mathbb {C}}$
that gives positive measure to non-empty open sets can be invariant under
$\widehat {\mathbb {C}}$
that gives positive measure to non-empty open sets can be invariant under
![]() $\mathcal {F}_a$
. Suppose by contradiction that
$\mathcal {F}_a$
. Suppose by contradiction that
![]() $\unicode{x3bb} $
is such a measure satisfying
$\unicode{x3bb} $
is such a measure satisfying
![]() $\tfrac 12\mathcal {F}_a^*\unicode{x3bb} =\unicode{x3bb} $
. In particular, we have that
$\tfrac 12\mathcal {F}_a^*\unicode{x3bb} =\unicode{x3bb} $
. In particular, we have that
![]() $\unicode{x3bb} ((\widehat {\mathbb {C}}\setminus \Delta _{\operatorname {J}_a})\setminus \mathcal {F}_a(\widehat {\mathbb {C}}\setminus \Delta _{J}))=0$
. On the other hand, note that
$\unicode{x3bb} ((\widehat {\mathbb {C}}\setminus \Delta _{\operatorname {J}_a})\setminus \mathcal {F}_a(\widehat {\mathbb {C}}\setminus \Delta _{J}))=0$
. On the other hand, note that
is closed in
![]() $\widehat {\mathbb {C}}$
. By Remark 2.9 part (1),
$\widehat {\mathbb {C}}$
. By Remark 2.9 part (1),
![]() $(\widehat {\mathbb {C}}\setminus \overline {\Delta _{\operatorname {J}_a}})\setminus \mathcal {F}_a(\widehat {\mathbb {C}}\setminus \Delta _{\operatorname {J}_a})$
is open and non-empty, contained in
$(\widehat {\mathbb {C}}\setminus \overline {\Delta _{\operatorname {J}_a}})\setminus \mathcal {F}_a(\widehat {\mathbb {C}}\setminus \Delta _{\operatorname {J}_a})$
is open and non-empty, contained in
![]() $(\widehat {\mathbb {C}}\setminus \Delta _{\operatorname {J}_a})\setminus \mathcal {F}_a(\widehat {\mathbb {C}}\setminus \Delta _{J})$
. This contradicts part
$(\widehat {\mathbb {C}}\setminus \Delta _{\operatorname {J}_a})\setminus \mathcal {F}_a(\widehat {\mathbb {C}}\setminus \Delta _{J})$
. This contradicts part
![]() $(3)$
of Remark 3.3, as
$(3)$
of Remark 3.3, as
![]() $\unicode{x3bb} $
cannot assign 0 measure to open sets.
$\unicode{x3bb} $
cannot assign 0 measure to open sets.
Remark 3.4. For a
![]() $(d,d)$
holomorphic correspondence F on compact Riemann surface X, the operator
$(d,d)$
holomorphic correspondence F on compact Riemann surface X, the operator
![]() $({1}/{d})F^*$
acts on the space
$({1}/{d})F^*$
acts on the space
![]() $L^2_{(1,0)}$
of
$L^2_{(1,0)}$
of
![]() $(1,0)$
-forms with
$(1,0)$
-forms with
![]() $L^2$
coefficients. In [Reference Dinh, Kaufmann and Wu15], the authors showed that the operator norm satisfies
$L^2$
coefficients. In [Reference Dinh, Kaufmann and Wu15], the authors showed that the operator norm satisfies
![]() $\Vert ({1}/{d})F^*\Vert \leq 1$
, with strict inequality for non weakly modular correspondences. This strict inequality is a key factor of their equidistribution result. However, this is never the case for
$\Vert ({1}/{d})F^*\Vert \leq 1$
, with strict inequality for non weakly modular correspondences. This strict inequality is a key factor of their equidistribution result. However, this is never the case for
![]() $F=\mathcal {F}_a$
,
$F=\mathcal {F}_a$
,
![]() $a\neq 1$
. We claim that
$a\neq 1$
. We claim that
and furthermore that the supremum is attained. To prove this, we use that
![]() $\|({1}/{d})F^*\phi \|_{L^2}=\|\phi \|_{L^2}$
for
$\|({1}/{d})F^*\phi \|_{L^2}=\|\phi \|_{L^2}$
for
![]() $\phi \in L^2_{(1,0)}$
if and only if for every
$\phi \in L^2_{(1,0)}$
if and only if for every
![]() $U\subset X\setminus B_1(\Gamma )$
and for every pair of local branches
$U\subset X\setminus B_1(\Gamma )$
and for every pair of local branches
![]() $f_1$
and
$f_1$
and
![]() $f_2$
of F on U, the equality
$f_2$
of F on U, the equality
![]() $f_1^*\phi =f_2^*\phi $
holds on U (see [Reference Dinh, Kaufmann and Wu15, Proposition 2.1]).
$f_1^*\phi =f_2^*\phi $
holds on U (see [Reference Dinh, Kaufmann and Wu15, Proposition 2.1]).
Observe that the form
![]() $\phi (z)=e^{-|Q(z)|}\,dz$
belongs to
$\phi (z)=e^{-|Q(z)|}\,dz$
belongs to
![]() $L^2_{(1,0)}$
for Q as in §2.2. Let
$L^2_{(1,0)}$
for Q as in §2.2. Let
![]() $U\subset \widehat {\mathbb {C}}\setminus B_1(\Gamma _{\operatorname {Cov^Q_0}})$
. Then the deleted covering correspondence
$U\subset \widehat {\mathbb {C}}\setminus B_1(\Gamma _{\operatorname {Cov^Q_0}})$
. Then the deleted covering correspondence
![]() $\operatorname {Cov^Q_0}$
sends z to the values w for which
$\operatorname {Cov^Q_0}$
sends z to the values w for which
![]() $({Q(z)-Q(w)})/({z-w})=0$
. Hence, any two local branches
$({Q(z)-Q(w)})/({z-w})=0$
. Hence, any two local branches
![]() $f_1$
and
$f_1$
and
![]() $f_2$
of
$f_2$
of
![]() $\operatorname {Cov^Q_0}$
satisfy
$\operatorname {Cov^Q_0}$
satisfy
![]() $f_1^*\phi (z)=Q(z)=f_2^*\phi (z)$
, and thus
$f_1^*\phi (z)=Q(z)=f_2^*\phi (z)$
, and thus
![]() $\Vert \tfrac 12\operatorname {Cov^Q_0}^*\!\Vert =1$
. Now note that
$\Vert \tfrac 12\operatorname {Cov^Q_0}^*\!\Vert =1$
. Now note that
![]() $\operatorname {J}_a$
is an involution, and hence
$\operatorname {J}_a$
is an involution, and hence
![]() $\operatorname {J}_a^*$
has operator norm
$\operatorname {J}_a^*$
has operator norm
![]() $1$
. Thus we can conclude that
$1$
. Thus we can conclude that
![]() $\Vert \tfrac 12\mathcal {F}_a^*\Vert =1$
as well, with supremum attained at
$\Vert \tfrac 12\mathcal {F}_a^*\Vert =1$
as well, with supremum attained at
![]() $\phi $
.
$\phi $
.
3.2 Limit sets
In this section, we define limit sets and give some properties. We will also prove that the application listed in [Reference Bharali and Sridharan1, §7] does not hold for our family of correspondences, and hence this is a new case to study equidistribution.
Remark 3.5. From Proposition 2.4, observe that
![]() $1\notin B_1(\Gamma _a)$
, and hence there is a holomorphic function g whose graph contains
$1\notin B_1(\Gamma _a)$
, and hence there is a holomorphic function g whose graph contains
![]() $(1,1)$
and is contained in
$(1,1)$
and is contained in
![]() $\Gamma _a$
. After the change of coordinates
$\Gamma _a$
. After the change of coordinates
![]() $\psi (z)=z-1$
, the function g has Taylor series expansion
$\psi (z)=z-1$
, the function g has Taylor series expansion
whenever
![]() $a\neq 7$
, and
$a\neq 7$
, and
for
![]() $a=7$
(see [Reference Bullett and Lomonaco4, Proposition 3.5]). In particular,
$a=7$
(see [Reference Bullett and Lomonaco4, Proposition 3.5]). In particular,
![]() $g^{\psi }$
has a parabolic fixed point at
$g^{\psi }$
has a parabolic fixed point at
![]() $0$
with multiplier
$0$
with multiplier
![]() $1$
.
$1$
.
In [Reference Bullett and Lomonaco4, Proposition 3.8], the authors showed that for each
![]() $a\in \mathcal {K}$
, after a small perturbation of
$a\in \mathcal {K}$
, after a small perturbation of
![]() $\partial \Delta _{\operatorname {Cov^Q_0}}$
and
$\partial \Delta _{\operatorname {Cov^Q_0}}$
and
![]() $\partial \Delta _{\operatorname {J}_a}$
around
$\partial \Delta _{\operatorname {J}_a}$
around
![]() $z=1$
, we can choose a Klein combination pair
$z=1$
, we can choose a Klein combination pair
![]() $(\Delta ^{\prime }_{\operatorname {Cov^Q_0}},\Delta ^{\prime }_{\operatorname {J}_a})$
so that
$(\Delta ^{\prime }_{\operatorname {Cov^Q_0}},\Delta ^{\prime }_{\operatorname {J}_a})$
so that
![]() $\partial \Delta ^{\prime }_{\operatorname {Cov^Q_0}}$
and
$\partial \Delta ^{\prime }_{\operatorname {Cov^Q_0}}$
and
![]() $\partial \Delta ^{\prime }_{\operatorname {J}_a}$
are both smooth at
$\partial \Delta ^{\prime }_{\operatorname {J}_a}$
are both smooth at
![]() $1$
, and transverse at
$1$
, and transverse at
![]() $1$
to the line generated by the repelling direction at
$1$
to the line generated by the repelling direction at
![]() $z=1$
for
$z=1$
for
![]() $a\neq 7$
, and to the real axis in the case
$a\neq 7$
, and to the real axis in the case
![]() $a=7$
.
$a=7$
.
For
![]() $a\in \mathcal {K}$
and
$a\in \mathcal {K}$
and
![]() $(\Delta _{\operatorname {Cov^Q_0}},\Delta _{\operatorname {J}_a})$
as above, we define
$(\Delta _{\operatorname {Cov^Q_0}},\Delta _{\operatorname {J}_a})$
as above, we define

to be the forward and backward limit set of
![]() $\mathcal {F}_a$
, respectively. These sets do not depend on the choice of the Klein combination pair
$\mathcal {F}_a$
, respectively. These sets do not depend on the choice of the Klein combination pair
![]() $(\Delta ^{\prime }_{\operatorname {Cov^Q_0}},\Delta ^{\prime }_{\operatorname {J}_a})$
as above.
$(\Delta ^{\prime }_{\operatorname {Cov^Q_0}},\Delta ^{\prime }_{\operatorname {J}_a})$
as above.
Lemma 3.6. Let
![]() $a\in \mathcal {K}$
. We have that:
$a\in \mathcal {K}$
. We have that:
-
(1)
 $\operatorname {J}_a(\Lambda _{a,\pm })=\Lambda _{a,\mp }$
and
$\operatorname {J}_a(\Lambda _{a,\pm })=\Lambda _{a,\mp }$
and
 $\operatorname {J}_a(\partial \Lambda _{a,\pm })=\partial \Lambda _{a,\mp }$
;
$\operatorname {J}_a(\partial \Lambda _{a,\pm })=\partial \Lambda _{a,\mp }$
; -
(2)
 $\Lambda _{a,-}\cap \Lambda _{a,+}=\lbrace 1\rbrace ;$
$\Lambda _{a,-}\cap \Lambda _{a,+}=\lbrace 1\rbrace ;$
-
(3) if
 $z\notin \Lambda _{a,-}$
, then there exists
$z\notin \Lambda _{a,-}$
, then there exists
 $n\geq 1$
so that
$n\geq 1$
so that
 $\mathcal {F}_a^{n}(z)\subset \widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {J}_a}$
, and if
$\mathcal {F}_a^{n}(z)\subset \widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {J}_a}$
, and if
 $z\notin \Lambda _{a,+}$
, then there exists
$z\notin \Lambda _{a,+}$
, then there exists
 $n\geq 1$
such that
$n\geq 1$
such that
 $\mathcal {F}_a^{-n}(z)\subset \Delta ^{\prime }_{\operatorname {J}_a}$
;
$\mathcal {F}_a^{-n}(z)\subset \Delta ^{\prime }_{\operatorname {J}_a}$
; -
(4)
 $\mathcal {F}_a^{-1}(\Lambda _{a,-})=\Lambda _{a,-}$
and
$\mathcal {F}_a^{-1}(\Lambda _{a,-})=\Lambda _{a,-}$
and
 $\mathcal {F}_a^{-1}(\partial \Lambda _{a,-})=\partial \Lambda _{a,-}$
; and
$\mathcal {F}_a^{-1}(\partial \Lambda _{a,-})=\partial \Lambda _{a,-}$
; and -
(5)
 $\mathcal {F}_a(\Lambda _{a,+})=\Lambda _{a,+}$
and
$\mathcal {F}_a(\Lambda _{a,+})=\Lambda _{a,+}$
and
 $\mathcal {F}_a(\partial \Lambda _{a,+})=\partial \Lambda _{a,+}$
.
$\mathcal {F}_a(\partial \Lambda _{a,+})=\partial \Lambda _{a,+}$
.
Proof. Since
![]() $\operatorname {J}_a$
is an involution sending
$\operatorname {J}_a$
is an involution sending
![]() $\overline {\Delta ^{\prime }_{\operatorname {J}_a}}$
and
$\overline {\Delta ^{\prime }_{\operatorname {J}_a}}$
and
![]() $\widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {J}_a}$
to each other, and since
$\widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {J}_a}$
to each other, and since
![]() $\operatorname {J}_a\circ \mathcal {F}_a^n=\mathcal {F}_a^{-n}\circ \operatorname {J}_a$
, then
$\operatorname {J}_a\circ \mathcal {F}_a^n=\mathcal {F}_a^{-n}\circ \operatorname {J}_a$
, then
 $$ \begin{align*}\operatorname{J}_a(\Lambda_{a,+})=\bigcap\limits_{n=0}^{\infty}\operatorname{J}_a\circ\mathcal{F}_a^n(\widehat{\mathbb{C}}\setminus\Delta^{\prime}_{\operatorname{J}_a})=\bigcap\limits_{n=0}^{\infty}\mathcal{F}_a^{-n}\circ\operatorname{J}_a(\widehat{\mathbb{C}}\setminus\Delta^{\prime}_{\operatorname{J}_a})=\Lambda_{a,-},\end{align*} $$
$$ \begin{align*}\operatorname{J}_a(\Lambda_{a,+})=\bigcap\limits_{n=0}^{\infty}\operatorname{J}_a\circ\mathcal{F}_a^n(\widehat{\mathbb{C}}\setminus\Delta^{\prime}_{\operatorname{J}_a})=\bigcap\limits_{n=0}^{\infty}\mathcal{F}_a^{-n}\circ\operatorname{J}_a(\widehat{\mathbb{C}}\setminus\Delta^{\prime}_{\operatorname{J}_a})=\Lambda_{a,-},\end{align*} $$
and applying
![]() $\operatorname {J}_a$
to both sides, we also get
$\operatorname {J}_a$
to both sides, we also get
![]() $\operatorname {J}_a(\Lambda _{a,-})=\Lambda _{a,+}$
. Moreover, since
$\operatorname {J}_a(\Lambda _{a,-})=\Lambda _{a,+}$
. Moreover, since
![]() $\operatorname {J}_a$
is continuous, note that
$\operatorname {J}_a$
is continuous, note that
Since
![]() $(\Delta ^{\prime }_{\operatorname {Cov^Q_0}},\Delta ^{\prime }_{\operatorname {J}_a})$
is a Klein combination pair,
$(\Delta ^{\prime }_{\operatorname {Cov^Q_0}},\Delta ^{\prime }_{\operatorname {J}_a})$
is a Klein combination pair,
![]() $\widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {J}_a}\subset \Delta ^{\prime }_{\operatorname {Cov^Q_0}}$
, so
$\widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {J}_a}\subset \Delta ^{\prime }_{\operatorname {Cov^Q_0}}$
, so
![]() $\partial \Delta ^{\prime }_{\operatorname {J}_a}\subset \overline {\Delta ^{\prime }_{\operatorname {Cov^Q_0}}}$
.
$\partial \Delta ^{\prime }_{\operatorname {J}_a}\subset \overline {\Delta ^{\prime }_{\operatorname {Cov^Q_0}}}$
.
If
![]() $z\in \Delta ^{\prime }_{\operatorname {Cov^Q_0}}$
, then
$z\in \Delta ^{\prime }_{\operatorname {Cov^Q_0}}$
, then
![]() $\operatorname {Cov^Q_0}(z)\subset \widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {J}_a}$
, and
$\operatorname {Cov^Q_0}(z)\subset \widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {J}_a}$
, and
![]() $\mathcal {F}_a(z)=\operatorname {J}_a\circ \operatorname {Cov^Q_0}(z)\subset \Delta ^{\prime }_{\operatorname {J}_a}$
. This is a contradiction, as
$\mathcal {F}_a(z)=\operatorname {J}_a\circ \operatorname {Cov^Q_0}(z)\subset \Delta ^{\prime }_{\operatorname {J}_a}$
. This is a contradiction, as
![]() $\mathcal {F}_a(z)$
must belong to
$\mathcal {F}_a(z)$
must belong to
![]() $\Lambda _{a,+}\subset \widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {J}_a}$
as well. Again, since
$\Lambda _{a,+}\subset \widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {J}_a}$
as well. Again, since
![]() $(\Delta ^{\prime }_{\operatorname {Cov^Q_0}},\Delta ^{\prime }_{\operatorname {J}_a})$
is a Klein combination pair, we have that
$(\Delta ^{\prime }_{\operatorname {Cov^Q_0}},\Delta ^{\prime }_{\operatorname {J}_a})$
is a Klein combination pair, we have that
![]() $z\in \partial \Delta ^{\prime }_{\operatorname {Cov^Q_0}}\cap \partial \Delta ^{\prime }_{\operatorname {J}_a}=\lbrace 1\rbrace $
and we conclude that
$z\in \partial \Delta ^{\prime }_{\operatorname {Cov^Q_0}}\cap \partial \Delta ^{\prime }_{\operatorname {J}_a}=\lbrace 1\rbrace $
and we conclude that
We prove part
![]() $(3)$
by the contrapositive. Suppose that for all n, there exists
$(3)$
by the contrapositive. Suppose that for all n, there exists
![]() $w\in \mathcal {F}_a^{n}(z)\cap (\widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {J}_a})$
, then
$w\in \mathcal {F}_a^{n}(z)\cap (\widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {J}_a})$
, then
![]() $z\in \mathcal {F}_a^{n}(w)\subset \mathcal {F}_a^{n}(\widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {J}_a})$
for all n. This implies that z must belong to
$z\in \mathcal {F}_a^{n}(w)\subset \mathcal {F}_a^{n}(\widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {J}_a})$
for all n. This implies that z must belong to
![]() $\Lambda _{a,-}$
. The other case is analogous.
$\Lambda _{a,-}$
. The other case is analogous.
It is immediate from the definition of
![]() $\Lambda _{a,-}$
and from part
$\Lambda _{a,-}$
and from part
![]() $(2)$
of Remark 2.9 that
$(2)$
of Remark 2.9 that
From this and Remark 2.6,
Observe that if
![]() $z\in \partial \Lambda _{a,-}\setminus \lbrace 1\rbrace \subset \Delta ^{\prime }_{\operatorname {Cov^Q_0}}$
, then
$z\in \partial \Lambda _{a,-}\setminus \lbrace 1\rbrace \subset \Delta ^{\prime }_{\operatorname {Cov^Q_0}}$
, then
Since
![]() $\Lambda _{a,-}\subset \overline {\Delta ^{\prime }_{\operatorname {J}_a}}$
, then we conclude that
$\Lambda _{a,-}\subset \overline {\Delta ^{\prime }_{\operatorname {J}_a}}$
, then we conclude that
Put
![]() $w\in \partial \Lambda _{a,-}$
and
$w\in \partial \Lambda _{a,-}$
and
![]() $z\in \mathcal {F}_a^{-1}(w)\subset \Lambda _{a,-}$
. We will show that
$z\in \mathcal {F}_a^{-1}(w)\subset \Lambda _{a,-}$
. We will show that
![]() $z\in \partial \Lambda _{a,-}$
by the contrapositive. Suppose
$z\in \partial \Lambda _{a,-}$
by the contrapositive. Suppose
![]() $w\neq 1$
and
$w\neq 1$
and
![]() $z\in \operatorname {int}(\Lambda _{a,-})$
. Then equation (12) implies that
$z\in \operatorname {int}(\Lambda _{a,-})$
. Then equation (12) implies that
From Remark 2.6, and the fact that
![]() $\Delta ^{\prime }_{\operatorname {J}_a}$
is open, we have that
$\Delta ^{\prime }_{\operatorname {J}_a}$
is open, we have that
![]() $\mathcal {F}_a(\operatorname {int}(\Lambda _{a,-}))\cap \Delta ^{\prime }_{\operatorname {J}_a}$
is open. Moreover, for each
$\mathcal {F}_a(\operatorname {int}(\Lambda _{a,-}))\cap \Delta ^{\prime }_{\operatorname {J}_a}$
is open. Moreover, for each
![]() $z'\in \operatorname {int}(\Lambda _{a,-})$
, the set
$z'\in \operatorname {int}(\Lambda _{a,-})$
, the set
![]() $\mathcal {F}_a(z')$
consists of a point in
$\mathcal {F}_a(z')$
consists of a point in
![]() $\Delta ^{\prime }_{\operatorname {J}_a}$
and one in
$\Delta ^{\prime }_{\operatorname {J}_a}$
and one in
![]() ${\widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {J}_a}}$
. Since the one in
${\widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {J}_a}}$
. Since the one in
![]() $\Delta ^{\prime }_{\operatorname {J}_a}$
is actually in
$\Delta ^{\prime }_{\operatorname {J}_a}$
is actually in
![]() $\Lambda _{a,-}$
by definition of
$\Lambda _{a,-}$
by definition of
![]() $\Lambda _{a,-}$
, then
$\Lambda _{a,-}$
, then
![]() $\mathcal {F}_a(\operatorname {int}(\Lambda _{a,-}))\cap \Delta ^{\prime }_{\operatorname {J}_a}\subset \Lambda _{a,-}$
. Then
$\mathcal {F}_a(\operatorname {int}(\Lambda _{a,-}))\cap \Delta ^{\prime }_{\operatorname {J}_a}\subset \Lambda _{a,-}$
. Then
![]() $w\in \operatorname {int}(\Lambda _{a,-})$
. This proves that
$w\in \operatorname {int}(\Lambda _{a,-})$
. This proves that
As for
![]() $w=1$
, we have that
$w=1$
, we have that
![]() $z\in \mathcal {F}_a^{-1}(1)=\lbrace -2,1\rbrace $
. We know
$z\in \mathcal {F}_a^{-1}(1)=\lbrace -2,1\rbrace $
. We know
![]() $1\in \partial \Lambda _{a,-}$
, so it suffices to show that
$1\in \partial \Lambda _{a,-}$
, so it suffices to show that
![]() $-2\in \partial \Lambda _{a,-}$
as well. Let
$-2\in \partial \Lambda _{a,-}$
as well. Let
![]() $U\subset \widehat {\mathbb {C}}$
be an open neighborhood of
$U\subset \widehat {\mathbb {C}}$
be an open neighborhood of
![]() $-2$
. From Remark 2.6, we have that
$-2$
. From Remark 2.6, we have that
![]() $\mathcal {F}_a(U)$
is an open neighborhood of
$\mathcal {F}_a(U)$
is an open neighborhood of
![]() $1$
. Since
$1$
. Since
![]() $1\in \partial \Delta ^{\prime }_{\operatorname {J}_a}$
, and
$1\in \partial \Delta ^{\prime }_{\operatorname {J}_a}$
, and
![]() $\partial \Delta ^{\prime }_{\operatorname {J}_a}$
is a Jordan curve, then there exists a point
$\partial \Delta ^{\prime }_{\operatorname {J}_a}$
is a Jordan curve, then there exists a point
![]() $w'\in U\cap \partial \Delta ^{\prime }_{\operatorname {J}_a}$
,
$w'\in U\cap \partial \Delta ^{\prime }_{\operatorname {J}_a}$
,
![]() $w'\neq 1$
. We have that
$w'\neq 1$
. We have that
![]() $\mathcal {F}_a(\partial \Delta ^{\prime }_{\operatorname {J}_a}\setminus \lbrace 1\rbrace )\subset \widehat {\mathbb {C}}\setminus \overline {\Delta ^{\prime }_{\operatorname {Cov^Q_0}}}$
, so
$\mathcal {F}_a(\partial \Delta ^{\prime }_{\operatorname {J}_a}\setminus \lbrace 1\rbrace )\subset \widehat {\mathbb {C}}\setminus \overline {\Delta ^{\prime }_{\operatorname {Cov^Q_0}}}$
, so
![]() $\mathcal {F}_a^{-1}(w')$
consists of two points,
$\mathcal {F}_a^{-1}(w')$
consists of two points,
![]() $z',z"\in \widehat {\mathbb {C}}\setminus \overline {\Delta ^{\prime }_{\operatorname {Cov^Q_0}}}$
, with
$z',z"\in \widehat {\mathbb {C}}\setminus \overline {\Delta ^{\prime }_{\operatorname {Cov^Q_0}}}$
, with
![]() $z'\in U$
. We will prove that
$z'\in U$
. We will prove that
![]() $z'\notin \Lambda _{a,-}$
by showing that
$z'\notin \Lambda _{a,-}$
by showing that
![]() $\mathcal {F}_a(z')\cap \Lambda _{a,-}=\emptyset $
, and thus
$\mathcal {F}_a(z')\cap \Lambda _{a,-}=\emptyset $
, and thus
![]() $-2\in \Lambda _{a,-}\setminus \operatorname {int}(\Lambda _{a,-})=\partial \Lambda _{a,-}$
. Indeed,
$-2\in \Lambda _{a,-}\setminus \operatorname {int}(\Lambda _{a,-})=\partial \Lambda _{a,-}$
. Indeed,
From part
![]() $(2)$
of Remark 2.9, we have that
$(2)$
of Remark 2.9, we have that
![]() $z'\notin \Lambda _{a,-}$
, and
$z'\notin \Lambda _{a,-}$
, and
![]() $-2\in \partial \Lambda _{a,-}$
as desired. This, together with equations (10), (11), and (13) prove part
$-2\in \partial \Lambda _{a,-}$
as desired. This, together with equations (10), (11), and (13) prove part
![]() $(4)$
.
$(4)$
.
We have that part
![]() $(1)$
of Remark 2.9 together with the definition of
$(1)$
of Remark 2.9 together with the definition of
![]() $\Lambda _{a,+}$
prove that
$\Lambda _{a,+}$
prove that
![]() $\mathcal {F}_a(\Lambda _{a,+})=\Lambda _{a,+}$
. To prove the rest of part
$\mathcal {F}_a(\Lambda _{a,+})=\Lambda _{a,+}$
. To prove the rest of part
![]() $(5)$
, we use part
$(5)$
, we use part
![]() $(4)$
together with the fact that
$(4)$
together with the fact that
![]() $\mathcal {F}_a=\operatorname {J}_a\circ \mathcal {F}_a^{-1}\circ \operatorname {J}_a$
and
$\mathcal {F}_a=\operatorname {J}_a\circ \mathcal {F}_a^{-1}\circ \operatorname {J}_a$
and
![]() $\operatorname {J}_a(\partial \Lambda _{a,\pm })=\partial \Lambda _{a,\mp }$
, as
$\operatorname {J}_a(\partial \Lambda _{a,\pm })=\partial \Lambda _{a,\mp }$
, as
![]() $\operatorname {J}_a$
is a continuous involution. Thus,
$\operatorname {J}_a$
is a continuous involution. Thus,
The following definition is from [Reference Bharali and Sridharan1, Reference McGehee26].
Definition 3.7. Let F be a holomorphic correspondence on X. We say that
![]() $\mathcal {R}\subset X$
is a repeller for F if there exists a set U such that
$\mathcal {R}\subset X$
is a repeller for F if there exists a set U such that
![]() $\mathcal {R}$
is contained in the interior of U, and
$\mathcal {R}$
is contained in the interior of U, and
 $$ \begin{align*}\mathcal{R}=\bigcap_{K\in\mathfrak{K}(U,F^{-1})} K,\end{align*} $$
$$ \begin{align*}\mathcal{R}=\bigcap_{K\in\mathfrak{K}(U,F^{-1})} K,\end{align*} $$
where
Bharali and Sridharan proved an equidistribution result similar to that in this paper [Reference Bharali and Sridharan1, Theorem 3.5] for correspondences having a repeller. Moreover, in [Reference Bharali and Sridharan1, §7.2], they showed that there is a set of pairs
![]() $(a,k)$
for which their result can be applied to the correspondence
$(a,k)$
for which their result can be applied to the correspondence
 $$ \begin{align*}\bigg(\frac{az+1}{z+1}\bigg)^2+\bigg(\frac{az+1}{z+1}\bigg)\bigg(\frac{aw-1}{w-1}\bigg)+\bigg(\frac{aw-1}{w-1}\bigg)^2=3k.\end{align*} $$
$$ \begin{align*}\bigg(\frac{az+1}{z+1}\bigg)^2+\bigg(\frac{az+1}{z+1}\bigg)\bigg(\frac{aw-1}{w-1}\bigg)+\bigg(\frac{aw-1}{w-1}\bigg)^2=3k.\end{align*} $$
For these correspondences (studied by Bullett and Harvey in [Reference Bullett and Harvey8]), there is a set
![]() $\Lambda _{a,-}$
analogous to that presented here (see [Reference Bullett and Penrose7] for the general definition of limit sets). For the pair
$\Lambda _{a,-}$
analogous to that presented here (see [Reference Bullett and Penrose7] for the general definition of limit sets). For the pair
![]() $(a,k)$
to work for their theorem, it is crucial for
$(a,k)$
to work for their theorem, it is crucial for
![]() $\partial \Lambda _{a,-}$
to be a repeller for the correspondence. Nevertheless, part
$\partial \Lambda _{a,-}$
to be a repeller for the correspondence. Nevertheless, part
![]() $(2)$
of Theorem 1.1 says this never happens for
$(2)$
of Theorem 1.1 says this never happens for
![]() $k=1$
and
$k=1$
and
![]() $|a-4|\leq 3$
.
$|a-4|\leq 3$
.
Proof of Theorem 1.1 part (2).
Let
![]() $U\subset \widehat {\mathbb {C}}$
contain
$U\subset \widehat {\mathbb {C}}$
contain
![]() $\partial \Lambda _{a,-}$
in its interior. We have that
$\partial \Lambda _{a,-}$
in its interior. We have that
![]() $1\in \partial \Lambda _{a,-}$
and is a parabolic fixed point of the function g whose graph is contained in
$1\in \partial \Lambda _{a,-}$
and is a parabolic fixed point of the function g whose graph is contained in
![]() $\Gamma _a$
, described in Remark 3.5. Take an attracting petal
$\Gamma _a$
, described in Remark 3.5. Take an attracting petal
![]() $\mathcal {P}$
at
$\mathcal {P}$
at
![]() $1$
so that
$1$
so that
![]() $\mathcal {P}\subset U$
. We first show that every
$\mathcal {P}\subset U$
. We first show that every
![]() $K\in \mathfrak {K}(U,\mathcal {F}_a^{-1})$
contains
$K\in \mathfrak {K}(U,\mathcal {F}_a^{-1})$
contains
![]() $\partial \Lambda _{a,-}\cup \mathcal {P}$
. Indeed, for every
$\partial \Lambda _{a,-}\cup \mathcal {P}$
. Indeed, for every
![]() $K\in \mathfrak {K}(U,\mathcal {F}_a^{-1})$
and some integer
$K\in \mathfrak {K}(U,\mathcal {F}_a^{-1})$
and some integer
![]() $n\geq 0$
,
$n\geq 0$
,
Moreover, from part (4) of Lemma 3.6, we have that
Putting equations (14) and (15) together, we get that every
![]() $K\in \mathfrak {K}(U,\mathcal {F}_a^{-1})$
contains the union
$K\in \mathfrak {K}(U,\mathcal {F}_a^{-1})$
contains the union
![]() $\partial \Lambda _{a,-}\cup \mathcal {P}$
, and therefore so does the intersection over all K. Since
$\partial \Lambda _{a,-}\cup \mathcal {P}$
, and therefore so does the intersection over all K. Since
![]() $\operatorname {int}(\partial \Lambda _{a,-})=\emptyset $
and
$\operatorname {int}(\partial \Lambda _{a,-})=\emptyset $
and
![]() $\operatorname {int}(\mathcal {P})\neq \emptyset $
, we have that
$\operatorname {int}(\mathcal {P})\neq \emptyset $
, we have that
 $$ \begin{align*}\partial\Lambda_{a,-}\subsetneq\partial\Lambda_{a,-}\cup\mathcal{P}\subset\bigcap_{K\in\mathfrak{K}(U,\mathcal{F}_a^{-1})} K.\end{align*} $$
$$ \begin{align*}\partial\Lambda_{a,-}\subsetneq\partial\Lambda_{a,-}\cup\mathcal{P}\subset\bigcap_{K\in\mathfrak{K}(U,\mathcal{F}_a^{-1})} K.\end{align*} $$
Since U is arbitrary, we conclude that
![]() $\partial \Lambda _{a,-}$
is not a repeller for
$\partial \Lambda _{a,-}$
is not a repeller for
![]() $\mathcal {F}_a$
.
$\mathcal {F}_a$
.
4 Exceptional set and periodic points
In this section, we will define a two-sided restriction of
![]() $\mathcal {F}_a$
and prove it is a proper holomorphic map of degree 2. We will find its exceptional set and that of
$\mathcal {F}_a$
and prove it is a proper holomorphic map of degree 2. We will find its exceptional set and that of
![]() $\mathcal {F}_a$
. This will be important for the next section, as it is the set of all points that may escape from the equidistribution property given in Theorem 1.2.
$\mathcal {F}_a$
. This will be important for the next section, as it is the set of all points that may escape from the equidistribution property given in Theorem 1.2.
The following definition is classical.
Definition 4.1. Let
![]() $f:U\to V$
be a holomorphic proper map, with
$f:U\to V$
be a holomorphic proper map, with
![]() $U,V$
open,
$U,V$
open,
![]() $U\subset V$
. For
$U\subset V$
. For
![]() $z\in U$
, we denote by
$z\in U$
, we denote by
![]() $[ z]$
the equivalence class of z by the equivalence relation
$[ z]$
the equivalence class of z by the equivalence relation
We say that z is exceptional for f if
![]() $[ z]$
is finite, and we call exceptional set the set
$[ z]$
is finite, and we call exceptional set the set
![]() $\mathcal {E}$
of all points that are exceptional for f.
$\mathcal {E}$
of all points that are exceptional for f.
Put
![]() $a\in \mathcal {K}$
and denote by
$a\in \mathcal {K}$
and denote by
![]() $f_a$
the two-sided restriction
$f_a$
the two-sided restriction
![]() , meaning
, meaning
![]() $f_a$
sends each
$f_a$
sends each
![]() $z\in \mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})$
to the unique point in
$z\in \mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})$
to the unique point in
![]() $\mathcal {F}_a(z)\cap \Delta ^{\prime }_{\operatorname {J}_a}$
. This it is a single-valued, continuous, and holomorphic 2-to-1 map (see [Reference Bullett and Lomonaco4, Proposition 3.4] and Theorem 4.2 below) that extends on a neighborhood of every point
$\mathcal {F}_a(z)\cap \Delta ^{\prime }_{\operatorname {J}_a}$
. This it is a single-valued, continuous, and holomorphic 2-to-1 map (see [Reference Bullett and Lomonaco4, Proposition 3.4] and Theorem 4.2 below) that extends on a neighborhood of every point
![]() $z\in \partial \mathcal {F}_a^{-1}(\Delta _{\operatorname {J}_a})\setminus \lbrace -2\rbrace $
. In particular,
$z\in \partial \mathcal {F}_a^{-1}(\Delta _{\operatorname {J}_a})\setminus \lbrace -2\rbrace $
. In particular,
![]() $f_a$
extends around
$f_a$
extends around
![]() $z=1$
and
$z=1$
and
![]() $f_a(1)=1$
. Since
$f_a(1)=1$
. Since
![]() $\Delta ^{\prime }_{\operatorname {J}_a}$
is open and
$\Delta ^{\prime }_{\operatorname {J}_a}$
is open and
![]() $f_a$
is continuous, then
$f_a$
is continuous, then
![]() $\mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})(=f_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a}))$
is open as well. Note that the analogous of part (2) of Remark 2.9 holds for
$\mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})(=f_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a}))$
is open as well. Note that the analogous of part (2) of Remark 2.9 holds for
![]() $\Delta ^{\prime }_{\operatorname {J}_a}$
and
$\Delta ^{\prime }_{\operatorname {J}_a}$
and
![]() $\Delta ^{\prime }_{\operatorname {Cov^Q_0}}$
instead, using the definition of Klein pair and the fact that
$\Delta ^{\prime }_{\operatorname {Cov^Q_0}}$
instead, using the definition of Klein pair and the fact that
![]() $\operatorname {J}_a$
is open. Thus,
$\operatorname {J}_a$
is open. Thus,
![]() $\mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})\subset \Delta ^{\prime }_{\operatorname {J}_a}$
.
$\mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})\subset \Delta ^{\prime }_{\operatorname {J}_a}$
.
The following theorem is the main result of this section.
Theorem 4.2. For each
![]() $a\in \mathcal {K}$
, we have the following.
$a\in \mathcal {K}$
, we have the following.
-
(1) The two-sided restriction
 $f_a:\mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})\to \Delta ^{\prime }_{\operatorname {J}_a}$
of
$f_a:\mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})\to \Delta ^{\prime }_{\operatorname {J}_a}$
of
 $\mathcal {F}_a$
is holomorphic and proper, of degree
$\mathcal {F}_a$
is holomorphic and proper, of degree
 $2$
.
$2$
. -
(2) The map
 $f_a$
has a critical point if and only if
$f_a$
has a critical point if and only if
 $2\in \widehat {\mathbb {C}}\setminus \overline {\Delta ^{\prime }_{\operatorname {J}_a}}$
. Furthermore, in that case, we have that the critical point is
$2\in \widehat {\mathbb {C}}\setminus \overline {\Delta ^{\prime }_{\operatorname {J}_a}}$
. Furthermore, in that case, we have that the critical point is
 $-$
1.
$-$
1. -
(3) The exceptional set
 $\mathcal {E}_{a,-}$
of
$\mathcal {E}_{a,-}$
of
 $f_a$
is non-empty if and only if
$f_a$
is non-empty if and only if
 $a=5$
. In that case,
$a=5$
. In that case,
 ${\mathcal {E}_{a,-}=\lbrace -1\rbrace }$
.
${\mathcal {E}_{a,-}=\lbrace -1\rbrace }$
.
Computing images and preimages under
![]() $\mathcal {F}_a$
, we see that when
$\mathcal {F}_a$
, we see that when
![]() $a=5$
, we have that
$a=5$
, we have that
![]() $\circlearrowright -1\mapsto 2\circlearrowleft $
. In the following section, it will be useful to use the full orbit of
$\circlearrowright -1\mapsto 2\circlearrowleft $
. In the following section, it will be useful to use the full orbit of
![]() $\mathcal {E}_{a,-}$
under
$\mathcal {E}_{a,-}$
under
![]() $\mathcal {F}_a$
, meaning
$\mathcal {F}_a$
, meaning

Proof of Theorem 4.2.
We first show part (1). Observe that
![]() $\infty $
and
$\infty $
and
![]() $\operatorname {J}_a(\infty )$
lie on opposite sides of
$\operatorname {J}_a(\infty )$
lie on opposite sides of
![]() $\partial\Delta^{\prime }_{{\operatorname{J}_a}}$
. Therefore,
$\partial\Delta^{\prime }_{{\operatorname{J}_a}}$
. Therefore,
![]() $(\infty ,({a+1})/{2})\notin (\mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})\times \Delta ^{\prime }_{\operatorname {J}_a})$
. In view of Proposition 2.4, this implies that for every
$(\infty ,({a+1})/{2})\notin (\mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})\times \Delta ^{\prime }_{\operatorname {J}_a})$
. In view of Proposition 2.4, this implies that for every
there there exists a neighborhood U of
![]() $(z_0,w_0)$
such that
$(z_0,w_0)$
such that
![]() $U\cap \Gamma _a$
is the graph of a holomorphic function either in z or in w. Therefore,
$U\cap \Gamma _a$
is the graph of a holomorphic function either in z or in w. Therefore,
![]() $\operatorname {Gr}(f_a)$
is an open subset of
$\operatorname {Gr}(f_a)$
is an open subset of
![]() $\Gamma _a\setminus \lbrace (\infty ,({a+1})/{2})\rbrace $
, which has no singularities. Thus,
$\Gamma _a\setminus \lbrace (\infty ,({a+1})/{2})\rbrace $
, which has no singularities. Thus,
![]() $\operatorname {Gr}(f_a)$
is a Riemann surface and
$\operatorname {Gr}(f_a)$
is a Riemann surface and
![]() $f_a$
is holomorphic.
$f_a$
is holomorphic.
It is clear that
![]() $f_a^{-1}(w)$
is compact for all
$f_a^{-1}(w)$
is compact for all
![]() $w\in \Delta _{\operatorname {J}_a}$
, since
$w\in \Delta _{\operatorname {J}_a}$
, since
Moreover,
![]() $f_a$
is a closed map, and therefore a proper map. Indeed, let
$f_a$
is a closed map, and therefore a proper map. Indeed, let
![]() $C\subset \mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})$
be closed. Then
$C\subset \mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})$
be closed. Then
![]() $C=C'\cap \mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})$
for some closed subset
$C=C'\cap \mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})$
for some closed subset
![]() $C'\subset \widehat {\mathbb {C}}$
. Observe that
$C'\subset \widehat {\mathbb {C}}$
. Observe that
![]() ${f_a(C)=\mathcal {F}_a(C')\cap \Delta ^{\prime }_{\operatorname {J}_a}}$
and that
${f_a(C)=\mathcal {F}_a(C')\cap \Delta ^{\prime }_{\operatorname {J}_a}}$
and that
By compactness of
![]() $\widehat {\mathbb {C}}$
,
$\widehat {\mathbb {C}}$
,
![]() $\pi _2$
is closed, and since both
$\pi _2$
is closed, and since both
![]() $\Gamma _a$
and
$\Gamma _a$
and
![]() $C'\times \widehat {\mathbb {C}}$
are closed subsets of
$C'\times \widehat {\mathbb {C}}$
are closed subsets of
![]() $\widehat {\mathbb {C}}\times \widehat {\mathbb {C}}$
, then
$\widehat {\mathbb {C}}\times \widehat {\mathbb {C}}$
, then
![]() $\mathcal {F}_a(C')$
is closed. Therefore,
$\mathcal {F}_a(C')$
is closed. Therefore,
![]() $f_a(C)$
is closed in
$f_a(C)$
is closed in
![]() $\Delta ^{\prime }_{\operatorname {J}_a}$
and
$\Delta ^{\prime }_{\operatorname {J}_a}$
and
![]() $f_a$
is a closed map. We conclude
$f_a$
is a closed map. We conclude
![]() $f_a$
is proper. Moreover, by definition of
$f_a$
is proper. Moreover, by definition of
![]() $f_a$
, every preimage z of a point
$f_a$
, every preimage z of a point
![]() $w\in \Delta ^{\prime }_{\operatorname {J}_a}$
belongs to the domain of
$w\in \Delta ^{\prime }_{\operatorname {J}_a}$
belongs to the domain of
![]() $f_a$
, and
$f_a$
, and
![]() $f_a(z)=w$
. Therefore,
$f_a(z)=w$
. Therefore,
![]() $f_a$
has degree
$f_a$
has degree
![]() $2$
, since
$2$
, since
![]() $\mathcal {F}_a$
has two preimages of a generic point in
$\mathcal {F}_a$
has two preimages of a generic point in
![]() $\Delta ^{\prime }_{\operatorname {J}_a}$
.
$\Delta ^{\prime }_{\operatorname {J}_a}$
.
We proceed to show part (2). Let
![]() $z_0$
be a critical point of
$z_0$
be a critical point of
![]() $f_a$
. Then
$f_a$
. Then
![]() $(z_0,f_a(z_0))$
belongs to
$(z_0,f_a(z_0))$
belongs to
Observe that
![]() $\mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})\subset \Delta ^{\prime }_{\operatorname {J}_a}$
and
$\mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})\subset \Delta ^{\prime }_{\operatorname {J}_a}$
and
![]() $1\notin \Delta ^{\prime }_{\operatorname {J}_a}$
, so
$1\notin \Delta ^{\prime }_{\operatorname {J}_a}$
, so
![]() $(1,\operatorname {J}_a(-2))\notin \mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})\times \Delta ^{\prime }_{\operatorname {J}_a}$
. Since we also have that
$(1,\operatorname {J}_a(-2))\notin \mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})\times \Delta ^{\prime }_{\operatorname {J}_a}$
. Since we also have that
![]() $\infty $
and
$\infty $
and
![]() $\operatorname {J}_a(\infty )$
lie on opposite sides of
$\operatorname {J}_a(\infty )$
lie on opposite sides of
![]() $\partial\Delta^{\prime }_{\operatorname {J}_a}$
and from Proposition 2.4, it must be the case that
$\partial\Delta^{\prime }_{\operatorname {J}_a}$
and from Proposition 2.4, it must be the case that
![]() $(z_0,f_a(z_0))=(-1,\operatorname {J}_a(2))$
. Thus,
$(z_0,f_a(z_0))=(-1,\operatorname {J}_a(2))$
. Thus,
![]() $z_0=-1$
and
$z_0=-1$
and
![]() ${\operatorname {J}_a(2)\in \Delta ^{\prime }_{\operatorname {J}_a}}$
, and therefore
${\operatorname {J}_a(2)\in \Delta ^{\prime }_{\operatorname {J}_a}}$
, and therefore
![]() $2\in \widehat {\mathbb {C}}\setminus \overline {\Delta ^{\prime }_{\operatorname {J}_a}}$
. To prove the reverse implication, note that whenever
$2\in \widehat {\mathbb {C}}\setminus \overline {\Delta ^{\prime }_{\operatorname {J}_a}}$
. To prove the reverse implication, note that whenever
![]() ${2\in \widehat {\mathbb {C}}\setminus \overline {\Delta ^{\prime }_{\operatorname {J}_a}}}$
, we have that
${2\in \widehat {\mathbb {C}}\setminus \overline {\Delta ^{\prime }_{\operatorname {J}_a}}}$
, we have that
![]() $\operatorname {J}_a(2)={2}/({3-a})\in \Delta ^{\prime }_{\operatorname {J}_a}$
, so there exists
$\operatorname {J}_a(2)={2}/({3-a})\in \Delta ^{\prime }_{\operatorname {J}_a}$
, so there exists
![]() $z_0\in \mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})$
such that
$z_0\in \mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})$
such that
![]() ${f_a(z_0)={2}/({3-a})}$
, by definition of
${f_a(z_0)={2}/({3-a})}$
, by definition of
![]() $f_a$
. Then
$f_a$
. Then
![]() $z_0=-1\in \mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})$
is a critical point for
$z_0=-1\in \mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})$
is a critical point for
![]() $f_a$
, as
$f_a$
, as
![]() $f_a$
has degree
$f_a$
has degree
![]() $2$
and
$2$
and
![]() $f_a^{-1}({2}/({3-a}))=\lbrace -1\rbrace $
. This proves that
$f_a^{-1}({2}/({3-a}))=\lbrace -1\rbrace $
. This proves that
![]() $f_a$
has a critical point if and only if
$f_a$
has a critical point if and only if
![]() $2\in \widehat {\mathbb {C}}\setminus \overline {\Delta ^{\prime }_{\operatorname {J}_a}}$
, and the critical point is
$2\in \widehat {\mathbb {C}}\setminus \overline {\Delta ^{\prime }_{\operatorname {J}_a}}$
, and the critical point is
![]() $z_0=-1$
.
$z_0=-1$
.
Finally, we prove part (3). Observe that if
![]() $w\in f_a^{-1}(z)$
, then
$w\in f_a^{-1}(z)$
, then
![]() $[ w]=[ z]$
, so
$[ w]=[ z]$
, so
![]() ${f_a^{-1}(\mathcal {E}_{a,-})\subset \mathcal {E}_{a,-}}$
and thus,
${f_a^{-1}(\mathcal {E}_{a,-})\subset \mathcal {E}_{a,-}}$
and thus,
![]() $|f_a^{-1}(\mathcal {E}_{a,-})|\leq |\mathcal {E}_{a,-}|$
. In particular, all points of
$|f_a^{-1}(\mathcal {E}_{a,-})|\leq |\mathcal {E}_{a,-}|$
. In particular, all points of
![]() $\mathcal {E}_{a,-}$
must have only one preimage under
$\mathcal {E}_{a,-}$
must have only one preimage under
![]() $f_a$
, and therefore, be critical. By part (2), if
$f_a$
, and therefore, be critical. By part (2), if
![]() $\mathcal {E}_{a,-}\neq \emptyset $
, then
$\mathcal {E}_{a,-}\neq \emptyset $
, then
![]() $-$
1 must be fixed. We know
$-$
1 must be fixed. We know
![]() $f_a(-1)={2}/({3-a})$
, and therefore if
$f_a(-1)={2}/({3-a})$
, and therefore if
![]() $\mathcal {E}_{a,-}\neq \emptyset $
, then
$\mathcal {E}_{a,-}\neq \emptyset $
, then
![]() ${2}/({3-a})=-1$
. Solving the equation, we get that
${2}/({3-a})=-1$
. Solving the equation, we get that
![]() $a=5$
. On the other hand, if
$a=5$
. On the other hand, if
![]() $a=5$
, then
$a=5$
, then
![]() $2\in \widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {J}_a}$
and therefore
$2\in \widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {J}_a}$
and therefore
![]() $z_0=-1$
is a critical point for
$z_0=-1$
is a critical point for
![]() $f_a$
that is fixed.
$f_a$
that is fixed.
Remark 4.3. Put
![]() $a\neq 1$
,
$a\neq 1$
,
![]() $|a-4|\leq 3$
, and
$|a-4|\leq 3$
, and
![]() $(\Delta _{\operatorname {Cov^Q_0}},\Delta _{\operatorname {J}_a})$
the Klein combination pair from [Reference Bullett and Lomonaco4] described in §2.2. Away from
$(\Delta _{\operatorname {Cov^Q_0}},\Delta _{\operatorname {J}_a})$
the Klein combination pair from [Reference Bullett and Lomonaco4] described in §2.2. Away from
![]() $z=1$
,
$z=1$
,
![]() $\Delta ^{\prime }_{\operatorname {J}_a}$
agrees with
$\Delta ^{\prime }_{\operatorname {J}_a}$
agrees with
![]() $\Delta _{\operatorname {J}_a}$
. Let r be the radius of the circle
$\Delta _{\operatorname {J}_a}$
. Let r be the radius of the circle
![]() $\partial \Delta _{\operatorname {J}_a}$
. Since the circle passes through a and has center
$\partial \Delta _{\operatorname {J}_a}$
. Since the circle passes through a and has center
![]() $(1+r)$
, then
$(1+r)$
, then
![]() $2\in \widehat {\mathbb {C}}\setminus \overline {\Delta _{\operatorname {J}_a}}$
if and only if
$2\in \widehat {\mathbb {C}}\setminus \overline {\Delta _{\operatorname {J}_a}}$
if and only if
![]() $r>\tfrac 12$
. Equivalently,
$r>\tfrac 12$
. Equivalently,
![]() $a\notin \overline {B}(\tfrac 32,\tfrac 12)$
. Since
$a\notin \overline {B}(\tfrac 32,\tfrac 12)$
. Since
![]() $2$
is away from
$2$
is away from
![]() $z=1$
,
$z=1$
,
![]() $2\in \widehat {\mathbb {C}}\setminus \overline {\Delta ^{\prime }_{\operatorname {J}_a}}$
if and only if
$2\in \widehat {\mathbb {C}}\setminus \overline {\Delta ^{\prime }_{\operatorname {J}_a}}$
if and only if
![]() $a\notin \overline {B}(\tfrac 32,\tfrac 12)$
as well.
$a\notin \overline {B}(\tfrac 32,\tfrac 12)$
as well.
-
• If
 $0<r\leq \tfrac 12$
, then
$0<r\leq \tfrac 12$
, then
 $f_a:\mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})\to \Delta ^{\prime }_{\operatorname {J}_a}$
has no critical points and hence is an unramified covering map. Since
$f_a:\mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})\to \Delta ^{\prime }_{\operatorname {J}_a}$
has no critical points and hence is an unramified covering map. Since
 $f_a$
is a 2-to-1 map, the Riemann–Hurwitz formula yields where
$f_a$
is a 2-to-1 map, the Riemann–Hurwitz formula yields where $$ \begin{align*}\chi(\mathcal{F}_a^{-1}(\Delta^{\prime}_{\operatorname{J}_a}))=2\chi(\Delta^{\prime}_{\operatorname{J}_a})=2,\end{align*} $$
$$ \begin{align*}\chi(\mathcal{F}_a^{-1}(\Delta^{\prime}_{\operatorname{J}_a}))=2\chi(\Delta^{\prime}_{\operatorname{J}_a})=2,\end{align*} $$
 $\chi $
denotes the Euler characteristic. Since
$\chi $
denotes the Euler characteristic. Since
 $f_a$
has degree 2,
$f_a$
has degree 2,
 $\mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})$
has at most two connected components, each of them with Euler characteristic at most
$\mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})$
has at most two connected components, each of them with Euler characteristic at most
 $1$
. It follows that
$1$
. It follows that
 $\mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})$
has exactly two connected components, each of them homeomorphic to a disk.
$\mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})$
has exactly two connected components, each of them homeomorphic to a disk.
-
• If
 $\tfrac 12<r<3$
, then
$\tfrac 12<r<3$
, then
 $f_a$
is a ramified covering of degree
$f_a$
is a ramified covering of degree
 $2$
with one critical point at
$2$
with one critical point at
 ${z_0=-1}$
, whose ramification index equals 2. Therefore, again by the Riemann–Hurwitz formula, we get that Let
${z_0=-1}$
, whose ramification index equals 2. Therefore, again by the Riemann–Hurwitz formula, we get that Let $$ \begin{align*}\chi(\mathcal{F}_a^{-1}(\Delta^{\prime}_{\operatorname{J}_a}))=2\chi(\Delta^{\prime}_{\operatorname{J}_a})-(2-1)=1.\end{align*} $$
$$ \begin{align*}\chi(\mathcal{F}_a^{-1}(\Delta^{\prime}_{\operatorname{J}_a}))=2\chi(\Delta^{\prime}_{\operatorname{J}_a})-(2-1)=1.\end{align*} $$
 $\Omega $
be the component of
$\Omega $
be the component of
 $\mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})$
that contains
$\mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})$
that contains
 $-$
1. Then
$-$
1. Then
 is not locally injective at
is not locally injective at
 $-$
1, and therefore of degree
$-$
1, and therefore of degree
 $2$
. Therefore,
$2$
. Therefore,
 $\mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})=\Omega $
has one connected component, which is homeomorphic to a circle, and mapped 2-to-1 onto
$\mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})=\Omega $
has one connected component, which is homeomorphic to a circle, and mapped 2-to-1 onto
 $\Delta ^{\prime }_{\operatorname {J}_a}$
.
$\Delta ^{\prime }_{\operatorname {J}_a}$
.
We finish this section by listing some properties of the periodic points of
![]() $\mathcal {F}_a$
. To do so, recall that for a holomorphic correspondence
$\mathcal {F}_a$
. To do so, recall that for a holomorphic correspondence
![]() $F$
on
$F$
on
![]() $X$
,
$X$
,
where
![]() $\Gamma ^{(n)}$
is the graph of
$\Gamma ^{(n)}$
is the graph of
![]() $F^n$
and
$F^n$
and
![]() $\mathfrak {D}_{X}$
is the diagonal in
$\mathfrak {D}_{X}$
is the diagonal in
![]() $X\times X$
. Note that
$X\times X$
. Note that
Lemma 4.4. For every
![]() $a\in \mathcal {K}$
, we have that:
$a\in \mathcal {K}$
, we have that:
-
(1)
 $\operatorname {Per}_n(\mathcal {F}_a)\subset \Lambda _{a,-}\cup \Lambda _{a,+}$
;
$\operatorname {Per}_n(\mathcal {F}_a)\subset \Lambda _{a,-}\cup \Lambda _{a,+}$
; -
(2)
 $\operatorname {J}_a(\operatorname {Per}_n(\mathcal {F}_a))=\operatorname {Per}_n(\mathcal {F}_a)$
;
$\operatorname {J}_a(\operatorname {Per}_n(\mathcal {F}_a))=\operatorname {Per}_n(\mathcal {F}_a)$
; -
(3)
 $\operatorname {J}_a(\operatorname {Per}_n(\mathcal {F}_a)\cap \Lambda _{a,\pm })=\operatorname {Per}_n(\mathcal {F}_a)\cap \Lambda _{a,\mp }$
; and
$\operatorname {J}_a(\operatorname {Per}_n(\mathcal {F}_a)\cap \Lambda _{a,\pm })=\operatorname {Per}_n(\mathcal {F}_a)\cap \Lambda _{a,\mp }$
; and -
(4)
 $\operatorname {Per}_n(\mathcal {F}_a)\cap \Lambda _{a,-}=\operatorname {Per}_n(f_a)$
.
$\operatorname {Per}_n(\mathcal {F}_a)\cap \Lambda _{a,-}=\operatorname {Per}_n(f_a)$
.
Proof. To prove part
![]() $(1)$
, suppose
$(1)$
, suppose
![]() $z\in \operatorname {Per}_n(\mathcal {F}_a)$
. If
$z\in \operatorname {Per}_n(\mathcal {F}_a)$
. If
![]() $z\in \overline {\Delta ^{\prime }_{\operatorname {J}_a}}$
, then
$z\in \overline {\Delta ^{\prime }_{\operatorname {J}_a}}$
, then
![]() $z\in \mathcal {F}_a^{-kn}(z)\subset \mathcal {F}_a^{-kn}(\overline {\Delta ^{\prime }_{\operatorname {J}_a}})$
for all
$z\in \mathcal {F}_a^{-kn}(z)\subset \mathcal {F}_a^{-kn}(\overline {\Delta ^{\prime }_{\operatorname {J}_a}})$
for all
![]() $k\geq 1$
. Since the sets
$k\geq 1$
. Since the sets
![]() $\mathcal {F}_a^{-k}(\overline {\Delta ^{\prime }_{\operatorname {J}_a}})$
are nested and their intersection is
$\mathcal {F}_a^{-k}(\overline {\Delta ^{\prime }_{\operatorname {J}_a}})$
are nested and their intersection is
![]() $\Lambda _{a,-}$
, then
$\Lambda _{a,-}$
, then
![]() $z\in \Lambda _{a,-}$
. On the other hand, if
$z\in \Lambda _{a,-}$
. On the other hand, if
![]() $z\notin \Lambda _{a,-}$
, by Lemma 3.6 part
$z\notin \Lambda _{a,-}$
, by Lemma 3.6 part
![]() $(3)$
, there exists
$(3)$
, there exists
![]() $m\geq 1$
so that
$m\geq 1$
so that
![]() $\mathcal {F}_a^m(z)\subset \widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {J}_a}$
. A similar argument as above shows that for all k sufficiently large,
$\mathcal {F}_a^m(z)\subset \widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {J}_a}$
. A similar argument as above shows that for all k sufficiently large,
![]() $z\in \mathcal {F}_a^k(\widehat {\mathbb {C}}\setminus \overline {\Delta ^{\prime }_{\operatorname {J}_a}})$
, which implies that
$z\in \mathcal {F}_a^k(\widehat {\mathbb {C}}\setminus \overline {\Delta ^{\prime }_{\operatorname {J}_a}})$
, which implies that
![]() $z\in \Lambda _{a,+}$
.
$z\in \Lambda _{a,+}$
.
Next, note that if
![]() $z\in \operatorname {Per}_n(\mathcal {F}_a)$
, then
$z\in \operatorname {Per}_n(\mathcal {F}_a)$
, then
![]() $z\in \mathcal {F}_a^{-n}(z)$
and
$z\in \mathcal {F}_a^{-n}(z)$
and
![]() $\operatorname {J}_a(z)\in \operatorname {J}_a(\mathcal {F}_a^{-n}(z))=\mathcal {F}_a^n(\operatorname {J}_a(z))$
. Therefore,
$\operatorname {J}_a(z)\in \operatorname {J}_a(\mathcal {F}_a^{-n}(z))=\mathcal {F}_a^n(\operatorname {J}_a(z))$
. Therefore,
![]() $\operatorname {J}_a(z)\in \operatorname {Per}_n(\mathcal {F}_a)$
as well. Since
$\operatorname {J}_a(z)\in \operatorname {Per}_n(\mathcal {F}_a)$
as well. Since
![]() $\operatorname {J}_a$
is an involution, this shows part
$\operatorname {J}_a$
is an involution, this shows part
![]() $(2)$
.
$(2)$
.
Recall from Remark 3.6 that
![]() $\operatorname {J}_a$
sends the limits sets to each other. Therefore,
$\operatorname {J}_a$
sends the limits sets to each other. Therefore,
![]() $\operatorname {J}_a(\operatorname {Per}_n(\mathcal {F}_a)\cap \Lambda _{a,-})=\operatorname {Per}_n(\mathcal {F}_a)\cap \Lambda _{a,+}$
, and again since
$\operatorname {J}_a(\operatorname {Per}_n(\mathcal {F}_a)\cap \Lambda _{a,-})=\operatorname {Per}_n(\mathcal {F}_a)\cap \Lambda _{a,+}$
, and again since
![]() $\operatorname {J}_a$
is an involution, we also have that
$\operatorname {J}_a$
is an involution, we also have that
This proves part
![]() $(3)$
.
$(3)$
.
Finally, we prove part
![]() $(4)$
. We have that for each
$(4)$
. We have that for each
![]() $z\in \mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})\cup \lbrace 1\rbrace $
,
$z\in \mathcal {F}_a^{-1}(\Delta ^{\prime }_{\operatorname {J}_a})\cup \lbrace 1\rbrace $
,
![]() $\mathcal {F}_a^{-n}(z)=f_a^{-n}(z)$
and part
$\mathcal {F}_a^{-n}(z)=f_a^{-n}(z)$
and part
![]() $(1)$
implies that all periodic points of
$(1)$
implies that all periodic points of
![]() $\mathcal {F}_a$
not in
$\mathcal {F}_a$
not in
![]() $\Lambda _{a,+}$
must belong to
$\Lambda _{a,+}$
must belong to
![]() $\Lambda _{a,-}$
. Since
$\Lambda _{a,-}$
. Since
![]() $z\in \operatorname {Per}_n(f_a)$
if and only if
$z\in \operatorname {Per}_n(f_a)$
if and only if
![]() $z\in f_a^{-n}(z)=\mathcal {F}_a^{-1}(z)$
, then
$z\in f_a^{-n}(z)=\mathcal {F}_a^{-1}(z)$
, then
5 Equidistribution of
 $\lbrace \mathcal {F}_a^n\rbrace _n$
$\lbrace \mathcal {F}_a^n\rbrace _n$
In this section, we prove Theorems 1.2 and 1.3 using the results from [Reference Freire, Lopes and Mañé20, Reference Ljubich24], together with [Reference Bullett and Lomonaco4, Reference Bullett and Lomonaco5].
Recall every rational map
![]() $P_A$
of the form
$P_A$
of the form
with
![]() $A\in \mathbb {C}$
, has critical points
$A\in \mathbb {C}$
, has critical points
![]() $\pm 1$
and a parabolic fixed point at
$\pm 1$
and a parabolic fixed point at
![]() $\infty $
with multiplier equal to
$\infty $
with multiplier equal to
![]() $1$
. Now note that in the coordinate
$1$
. Now note that in the coordinate
![]() $\phi (z)=1/z$
, we have that
$\phi (z)=1/z$
, we have that
near
![]() $0$
. Thus,
$0$
. Thus,
![]() $z=0$
is a fixed point of
$z=0$
is a fixed point of
![]() $P_A^{\phi }$
with multiplicity
$P_A^{\phi }$
with multiplicity
![]() $2$
if
$2$
if
![]() $A\neq 0$
, and
$A\neq 0$
, and
![]() $3$
if
$3$
if
![]() $A=0$
. We conclude that for
$A=0$
. We conclude that for
![]() $A\neq 0$
, the parabolic fixed point has multiplicity
$A\neq 0$
, the parabolic fixed point has multiplicity
![]() $1$
, and
$1$
, and
![]() $3$
for
$3$
for
![]() $A=0$
.
$A=0$
.
For
![]() $A\in \mathbb {C}\setminus \lbrace 0\rbrace $
, let
$A\in \mathbb {C}\setminus \lbrace 0\rbrace $
, let
![]() $\Omega _A$
be the basin of attraction of
$\Omega _A$
be the basin of attraction of
![]() $\infty $
, and for
$\infty $
, and for
![]() $A=0$
, we make the choice
$A=0$
, we make the choice
![]() $\Omega _0=\lbrace x+iy| x,y\in \mathbb {R},x>0\rbrace $
. We define the filled Julia set of
$\Omega _0=\lbrace x+iy| x,y\in \mathbb {R},x>0\rbrace $
. We define the filled Julia set of
![]() $P_A$
as the set
$P_A$
as the set
Remark 5.1. No periodic points of
![]() $P_A$
live in
$P_A$
live in
![]() $\Omega _A$
. Indeed, it is clear that points in
$\Omega _A$
. Indeed, it is clear that points in
![]() $\Omega _A$
for
$\Omega _A$
for
![]() $A\neq 0$
cannot be periodic, as their iterates converge to
$A\neq 0$
cannot be periodic, as their iterates converge to
![]() $\infty $
. Moreover, it is easy to check that if
$\infty $
. Moreover, it is easy to check that if
![]() $\Re (z)$
denotes the real part of
$\Re (z)$
denotes the real part of
![]() $z\neq 0$
, then
$z\neq 0$
, then
![]() $\Re (P_A(z))=\Re (z)({|z|^2+1})/{|z|^2}$
. Then
$\Re (P_A(z))=\Re (z)({|z|^2+1})/{|z|^2}$
. Then
![]() $\Omega _0$
is completely invariant and has no periodic points. Therefore, for all
$\Omega _0$
is completely invariant and has no periodic points. Therefore, for all
![]() $A\in \mathbb {C}$
, we have that
$A\in \mathbb {C}$
, we have that
![]() $\operatorname {Per}_n(P_A)\subset K_{P_A}$
, for all
$\operatorname {Per}_n(P_A)\subset K_{P_A}$
, for all
![]() $n\geq 1$
.
$n\geq 1$
.
Lemma 5.2. For every
![]() $a\in \mathcal {K}$
, there exists a measure
$a\in \mathcal {K}$
, there exists a measure
![]() $\mu _-$
with
$\mu _-$
with
![]() $\operatorname {supp}(\mu _-)=\partial \Lambda _{a,-}$
such that
$\operatorname {supp}(\mu _-)=\partial \Lambda _{a,-}$
such that
weakly, for all
![]() $z_0\in \Delta _{\operatorname {J}_a}\setminus \mathcal {E}_{a,-}$
.
$z_0\in \Delta _{\operatorname {J}_a}\setminus \mathcal {E}_{a,-}$
.
Here,
![]() $\mathcal {E}_{a,-}$
is the exceptional set of the two-sided restriction
$\mathcal {E}_{a,-}$
is the exceptional set of the two-sided restriction
![]() $f_a$
of
$f_a$
of
![]() $\mathcal {F}_a$
that leaves
$\mathcal {F}_a$
that leaves
![]() $\Lambda _{a,-}$
invariant, described in §4.
$\Lambda _{a,-}$
invariant, described in §4.
Proof. From the previous section, we can see that the two-sided restriction
![]() $f_a$
can extend around
$f_a$
can extend around
![]() $1$
. In [Reference Bullett and Lomonaco4, Proposition 5.2], the authors proved the existence of closed topological disks
$1$
. In [Reference Bullett and Lomonaco4, Proposition 5.2], the authors proved the existence of closed topological disks
![]() $V^{\prime }_a$
and
$V^{\prime }_a$
and
![]() $V_a$
containing
$V_a$
containing
![]() $\Lambda _{a,-}$
with
$\Lambda _{a,-}$
with
![]() $V^{\prime }_a=\mathcal {F}_a^{-1}(V_a)\subset V_a$
and satisfying most properties for
$V^{\prime }_a=\mathcal {F}_a^{-1}(V_a)\subset V_a$
and satisfying most properties for
![]() $f_a$
to be a parabolic-like map from
$f_a$
to be a parabolic-like map from
![]() $V^{\prime }_a$
and
$V^{\prime }_a$
and
![]() $V_a$
. Moreover, from the proof of [Reference Bullett and Lomonaco4, Theorem B], there exists a neighborhood U of
$V_a$
. Moreover, from the proof of [Reference Bullett and Lomonaco4, Theorem B], there exists a neighborhood U of
![]() $\Lambda _{a,-}$
,
$\Lambda _{a,-}$
,
![]() $A\in\mathbb{C}$
and a quasiconformal map
$A\in\mathbb{C}$
and a quasiconformal map
![]() ${h:U\cap V^{\prime }_a\cap \to h(U)\cap V_a}$
such that
${h:U\cap V^{\prime }_a\cap \to h(U)\cap V_a}$
such that
![]() $h\circ f=P_A\circ h$
, where
$h\circ f=P_A\circ h$
, where
![]() $P_A$
is as in equation (16). Such conjugacy sends
$P_A$
is as in equation (16). Such conjugacy sends
![]() $\Lambda _{a,-}$
onto the filled Julia set
$\Lambda _{a,-}$
onto the filled Julia set
![]() $K_{P_A}$
of
$K_{P_A}$
of
![]() $P_A$
.
$P_A$
.
From [Reference Freire, Lopes and Mañé20, Reference Ljubich24], there exists a measure
![]() $\tilde {\mu }_A$
on
$\tilde {\mu }_A$
on
![]() $\widehat {\mathbb {C}}$
supported on the Julia set
$\widehat {\mathbb {C}}$
supported on the Julia set
![]() $\mathcal {J}_{P_A}$
of
$\mathcal {J}_{P_A}$
of
![]() $P_A$
, such that for all
$P_A$
, such that for all
![]() $z_0\in \widehat {\mathbb {C}}$
not in the exceptional set E of
$z_0\in \widehat {\mathbb {C}}$
not in the exceptional set E of
![]() $P_A$
,
$P_A$
,
![]() $(1/2^n)(P_A^n)^*\delta _{z_0}$
is weakly convergent to
$(1/2^n)(P_A^n)^*\delta _{z_0}$
is weakly convergent to
![]() $\tilde {\mu }_A$
.
$\tilde {\mu }_A$
.
Recall
![]() $\Lambda _{a,-}$
is the intersection of the nested compact sets
$\Lambda _{a,-}$
is the intersection of the nested compact sets
![]() $\mathcal {F}_a^{-1}(\overline {\Delta ^{\prime }_{\operatorname {J}_a}})$
. Thus, there exists
$\mathcal {F}_a^{-1}(\overline {\Delta ^{\prime }_{\operatorname {J}_a}})$
. Thus, there exists
![]() $N\in \mathbb {N}$
such that
$N\in \mathbb {N}$
such that
![]() $\mathcal {F}_a^n(\overline {\Delta ^{\prime }_{\operatorname {J}_a}})\subset U\cap V^{\prime }_a$
, for all
$\mathcal {F}_a^n(\overline {\Delta ^{\prime }_{\operatorname {J}_a}})\subset U\cap V^{\prime }_a$
, for all
![]() $n\geq N$
. Observe as well that
$n\geq N$
. Observe as well that
![]() $h^{-1}(E)=\mathcal {E}_{a,-}$
as elements in
$h^{-1}(E)=\mathcal {E}_{a,-}$
as elements in
![]() $\mathcal {E}_{a,-}$
must have only one preimage and h is a homeomorphism, and the analogous holds for E and
$\mathcal {E}_{a,-}$
must have only one preimage and h is a homeomorphism, and the analogous holds for E and
![]() $h^{-1}$
.
$h^{-1}$
.
Now take
![]() $z_0\in \overline {\Delta ^{\prime }_{\operatorname {J}_a}}\setminus \mathcal {E}_{a,-}$
. Then,
$z_0\in \overline {\Delta ^{\prime }_{\operatorname {J}_a}}\setminus \mathcal {E}_{a,-}$
. Then,
![]() $f_a^{-N}(z_0)=\mathcal {F}_a^{-N}(z_0)\subset U\cap V^{\prime }_a$
. Then for each
$f_a^{-N}(z_0)=\mathcal {F}_a^{-N}(z_0)\subset U\cap V^{\prime }_a$
. Then for each
![]() ${\zeta \in f_a^{-N}(z_0)}$
, we have that
${\zeta \in f_a^{-N}(z_0)}$
, we have that
![]() $h(\zeta )\notin E$
and
$h(\zeta )\notin E$
and
![]() $(1/2^n)(P_A^n)^*\delta _{h(\zeta )}$
is weakly convergent to
$(1/2^n)(P_A^n)^*\delta _{h(\zeta )}$
is weakly convergent to
![]() $\tilde {\mu }_A$
. Note that
$\tilde {\mu }_A$
. Note that
![]() $\delta _{h(\zeta )}=h_*\delta _{\zeta }$
, and therefore for
$\delta _{h(\zeta )}=h_*\delta _{\zeta }$
, and therefore for
![]() $n\geq N$
,
$n\geq N$
,
 $$ \begin{align*}\frac{1}{2^n}(P_A^n)^*\delta_{h(\zeta)}=\frac{1}{2^n}(h^{-1}\circ P_A^n)^*\delta_{\zeta}=\frac{1}{2^n}(f_a^n\circ h^{-1})^*\delta_{\zeta}=h_*\bigg(\frac{1}{2^n}(f_a^n)^*\delta_{\zeta}\bigg).\end{align*} $$
$$ \begin{align*}\frac{1}{2^n}(P_A^n)^*\delta_{h(\zeta)}=\frac{1}{2^n}(h^{-1}\circ P_A^n)^*\delta_{\zeta}=\frac{1}{2^n}(f_a^n\circ h^{-1})^*\delta_{\zeta}=h_*\bigg(\frac{1}{2^n}(f_a^n)^*\delta_{\zeta}\bigg).\end{align*} $$
Since the left-hand side is weakly convergent to
![]() $\tilde {\mu }_A$
, then
$\tilde {\mu }_A$
, then
![]() $(1/2^n)(f_a^n)^*\delta _{\zeta }$
is weakly convergent to
$(1/2^n)(f_a^n)^*\delta _{\zeta }$
is weakly convergent to
![]() , which is supported on
, which is supported on
![]() $h^{-1}(\mathcal {J}_{P_A})=\partial \Lambda _{a,-}$
. Thus,
$h^{-1}(\mathcal {J}_{P_A})=\partial \Lambda _{a,-}$
. Thus,
 $$ \begin{align*}\frac{1}{2^n}(f_a^n)^*\delta_{z_0}=\frac{1}{2^N}\sum\limits_{\zeta\in f_a^{-N}(z_0)}\nu_{f_a^N}(\zeta)\frac{1}{2^{n-N}}(f_a^{n-N})^*\delta_{\zeta}\end{align*} $$
$$ \begin{align*}\frac{1}{2^n}(f_a^n)^*\delta_{z_0}=\frac{1}{2^N}\sum\limits_{\zeta\in f_a^{-N}(z_0)}\nu_{f_a^N}(\zeta)\frac{1}{2^{n-N}}(f_a^{n-N})^*\delta_{\zeta}\end{align*} $$
is weakly convergent to
![]() $\mu _-$
as desired.
$\mu _-$
as desired.
Proof of Theorem 1.2.
Let
![]() $\mu _-$
be as in Lemma 5.2 and put
$\mu _-$
be as in Lemma 5.2 and put
. Clearly,
![]() $\operatorname {supp}(\mu _+)=\partial \Lambda _{a,+}$
. Denote by
$\operatorname {supp}(\mu _+)=\partial \Lambda _{a,+}$
. Denote by
![]() $\delta _{z_0}$
the Dirac measure at
$\delta _{z_0}$
the Dirac measure at
![]() $z_0$
. If
$z_0$
. If
![]() $z_0\in \widehat {\mathbb {C}}\setminus (\Lambda _{a,-}\cup \mathcal {E}_a)$
, there exists
$z_0\in \widehat {\mathbb {C}}\setminus (\Lambda _{a,-}\cup \mathcal {E}_a)$
, there exists
![]() $n_0\in \mathbb {Z}^+\cup \lbrace 0\rbrace $
such that
$n_0\in \mathbb {Z}^+\cup \lbrace 0\rbrace $
such that
![]() ${\mathcal {F}_a^{n_0}(z_0)\cap \overline {\Delta ^{\prime }_{\operatorname {J}_a}}=\emptyset }$
by part
${\mathcal {F}_a^{n_0}(z_0)\cap \overline {\Delta ^{\prime }_{\operatorname {J}_a}}=\emptyset }$
by part
![]() $(3)$
of Lemma 3.6. In particular, this gives us that
$(3)$
of Lemma 3.6. In particular, this gives us that
![]() $\mathcal {F}_a^{n_0}(z_0)$
is contained in
$\mathcal {F}_a^{n_0}(z_0)$
is contained in
![]() $\widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {J}_a}$
, and therefore
$\widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {J}_a}$
, and therefore
![]() ${\mathcal {F}_a^n(z_0)\subset \widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {J}_a}}$
, for all
${\mathcal {F}_a^n(z_0)\subset \widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {J}_a}}$
, for all
![]() ${n\geq n_0}$
. In addition, for every
${n\geq n_0}$
. In addition, for every
![]() $z_j\in \mathcal {F}_a^{n_0}(z_0)$
,
$z_j\in \mathcal {F}_a^{n_0}(z_0)$
,
![]() $\operatorname {J}_a(z_j)\notin \mathcal {E}_{a,-}$
. Thus, for such a
$\operatorname {J}_a(z_j)\notin \mathcal {E}_{a,-}$
. Thus, for such a
![]() $z_0$
, we get that
$z_0$
, we get that

weakly, as
![]() $n\to \infty $
, where
$n\to \infty $
, where
![]() $\Gamma ^{(n_0)}$
is the graph of
$\Gamma ^{(n_0)}$
is the graph of
![]() $\mathcal {F}_a^{n_0}$
.
$\mathcal {F}_a^{n_0}$
.
Now observe that the two-sided restriction
![]() $f_a$
of
$f_a$
of
![]() $\mathcal {F}_a$
sends
$\mathcal {F}_a$
sends
![]() $\Lambda _{a,-}$
to itself. Indeed, note that the sets
$\Lambda _{a,-}$
to itself. Indeed, note that the sets
![]() $\mathcal {F}_a^{-n}(\overline {\Delta ^{\prime }_{\operatorname {J}_a}})$
are nested and if
$\mathcal {F}_a^{-n}(\overline {\Delta ^{\prime }_{\operatorname {J}_a}})$
are nested and if
![]() $f_a(z)\notin \mathcal {F}_a^{-n}(\overline {\Delta ^{\prime }_{\operatorname {J}_a}})$
for some
$f_a(z)\notin \mathcal {F}_a^{-n}(\overline {\Delta ^{\prime }_{\operatorname {J}_a}})$
for some
![]() $n\in \mathbb {Z}^+$
, then
$n\in \mathbb {Z}^+$
, then
![]() ${z\notin \mathcal {F}_a^{n-1}(\overline {\Delta ^{\prime }_{\operatorname {J}_a}})\supset \Lambda _{a,-}}$
. Note as well that
${z\notin \mathcal {F}_a^{n-1}(\overline {\Delta ^{\prime }_{\operatorname {J}_a}})\supset \Lambda _{a,-}}$
. Note as well that
![]() $-2\in \mathcal {F}_a^{-1}(1)$
and
$-2\in \mathcal {F}_a^{-1}(1)$
and
![]() $1\in \Lambda _{a,-}$
, so
$1\in \Lambda _{a,-}$
, so
![]() ${-2\in \Lambda _{a,-}}$
. Define
${-2\in \Lambda _{a,-}}$
. Define
![]() $\tilde {f_a}:\Lambda _{a,-}\to (\widehat {\mathbb {C}}\setminus \overline {\Delta ^{\prime }_{\operatorname {J}_a}})\cup \lbrace 1\rbrace $
by
$\tilde {f_a}:\Lambda _{a,-}\to (\widehat {\mathbb {C}}\setminus \overline {\Delta ^{\prime }_{\operatorname {J}_a}})\cup \lbrace 1\rbrace $
by
![]() $\tilde {f_a}(z)=w$
, where
$\tilde {f_a}(z)=w$
, where
![]() $\mathcal {F}_a(z)\setminus \lbrace f_a(z)\rbrace =\lbrace w\rbrace $
for
$\mathcal {F}_a(z)\setminus \lbrace f_a(z)\rbrace =\lbrace w\rbrace $
for
![]() ${z\neq -2}$
, and
${z\neq -2}$
, and
![]() $\tilde {f_a}(-2)=f_a(-2)=1$
for
$\tilde {f_a}(-2)=f_a(-2)=1$
for
![]() $z\in \mathcal {F}_a^{-1}(1)\setminus \lbrace 1\rbrace $
. Then for
$z\in \mathcal {F}_a^{-1}(1)\setminus \lbrace 1\rbrace $
. Then for
![]() $z_0\in \Lambda _{a,-}\setminus \mathcal {E}_a$
, we have that
$z_0\in \Lambda _{a,-}\setminus \mathcal {E}_a$
, we have that
![]() $\mathcal {F}_a(z_0)=\lbrace f_a(z_0),\tilde {f_a}(z_0)\rbrace $
, and
$\mathcal {F}_a(z_0)=\lbrace f_a(z_0),\tilde {f_a}(z_0)\rbrace $
, and
 $$ \begin{align*} \frac{1}{2}(\mathcal{F}_a)_*\delta_{z_0} &= \frac{1}{2}\delta_{f_a(z_0)}+\frac{1}{2}\delta_{\tilde{f_a}(z_0)},\\ \frac{1}{4}(\mathcal{F}_a^2)_*\delta_{z_0} &= \frac{1}{4}\delta_{{f_a}^2(z_0)}+\frac{1}{4}\delta_{\tilde{f_a}\circ f_a(z_0)}+\frac{1}{2}(\mathcal{F}_a)_*\delta_{\tilde{f_a}(z_0)},\\ \frac{1}{8}(\mathcal{F}_a^3)_*\delta_{z_0} &= \frac{1}{8}\delta_{{f_a}^3(z_0)}+\frac{1}{8}\delta_{\tilde{f_a}\circ {f_a}^2(z_0)}+\frac{1}{4}(\mathcal{F}_a)_*\delta_{\tilde{f_a}\circ f_a(z_0)}+\frac{1}{2}(\mathcal{F}_a^2)_*\delta_{\tilde{f_a}(z_0)},\\ &\ \ \vdots \\ \frac{1}{2^n}(\mathcal{F}_a^n)_*\delta_{z_0} &= \frac{1}{2^n}\delta_{{f_a}^n(z_0)}+\sum\limits_{j=1}^n \frac{1}{2^j}(\mathcal{F}_a^{n-j})_*\delta_{\tilde{f_a}\circ {f_a}^{j-1}(z_0)}. \end{align*} $$
$$ \begin{align*} \frac{1}{2}(\mathcal{F}_a)_*\delta_{z_0} &= \frac{1}{2}\delta_{f_a(z_0)}+\frac{1}{2}\delta_{\tilde{f_a}(z_0)},\\ \frac{1}{4}(\mathcal{F}_a^2)_*\delta_{z_0} &= \frac{1}{4}\delta_{{f_a}^2(z_0)}+\frac{1}{4}\delta_{\tilde{f_a}\circ f_a(z_0)}+\frac{1}{2}(\mathcal{F}_a)_*\delta_{\tilde{f_a}(z_0)},\\ \frac{1}{8}(\mathcal{F}_a^3)_*\delta_{z_0} &= \frac{1}{8}\delta_{{f_a}^3(z_0)}+\frac{1}{8}\delta_{\tilde{f_a}\circ {f_a}^2(z_0)}+\frac{1}{4}(\mathcal{F}_a)_*\delta_{\tilde{f_a}\circ f_a(z_0)}+\frac{1}{2}(\mathcal{F}_a^2)_*\delta_{\tilde{f_a}(z_0)},\\ &\ \ \vdots \\ \frac{1}{2^n}(\mathcal{F}_a^n)_*\delta_{z_0} &= \frac{1}{2^n}\delta_{{f_a}^n(z_0)}+\sum\limits_{j=1}^n \frac{1}{2^j}(\mathcal{F}_a^{n-j})_*\delta_{\tilde{f_a}\circ {f_a}^{j-1}(z_0)}. \end{align*} $$
Since
![]() $(1/2^n)\delta _{{f_a}^n(z_0)}$
has mass
$(1/2^n)\delta _{{f_a}^n(z_0)}$
has mass
![]() ${1}/{2^n}$
, then it is weakly convergent to a measure with zero mass. Put
${1}/{2^n}$
, then it is weakly convergent to a measure with zero mass. Put

If we truncate the sum defining
![]() $\mu _n$
at
$\mu _n$
at
![]() $N<n$
, we obtain a sequence
$N<n$
, we obtain a sequence
![]() $\mu _n^{(N)}=\sum \nolimits _{j=1}^N\mu _{n,j}$
satisfying
$\mu _n^{(N)}=\sum \nolimits _{j=1}^N\mu _{n,j}$
satisfying
![]() $\mu _n^{(N)}\to \sum \nolimits _{j=1}^N(1/2^j)\mu _+=(1-2^{-N})\mu _+$
weakly. Let
$\mu _n^{(N)}\to \sum \nolimits _{j=1}^N(1/2^j)\mu _+=(1-2^{-N})\mu _+$
weakly. Let
![]() $\varphi :\widehat {\mathbb {C}}\to \mathbb {R}$
be continuous and
$\varphi :\widehat {\mathbb {C}}\to \mathbb {R}$
be continuous and
![]() $\varepsilon>0$
. Choose
$\varepsilon>0$
. Choose
![]() $N\in \mathbb {Z}^+$
big so that
$N\in \mathbb {Z}^+$
big so that
![]() $(3/2^N)\sup |\varphi |<\varepsilon $
, and
$(3/2^N)\sup |\varphi |<\varepsilon $
, and
![]() $n>N$
such that
$n>N$
such that
 $$ \begin{align*}\bigg|\int\varphi \,d\mu_n^{(N)}-(1-2^{-N})\int\varphi \,d\mu_+\bigg|<\frac{1}{2^N}\sup|\varphi|\end{align*} $$
$$ \begin{align*}\bigg|\int\varphi \,d\mu_n^{(N)}-(1-2^{-N})\int\varphi \,d\mu_+\bigg|<\frac{1}{2^N}\sup|\varphi|\end{align*} $$
by the convergence
![]() $\mu _n^{(N)}\to (1-2^{-N})\mu _+$
. Then,
$\mu _n^{(N)}\to (1-2^{-N})\mu _+$
. Then,
 $$ \begin{align*} \bigg|\int\varphi \,d\mu_n^{(N)}-\int\varphi \,d\mu_+\bigg|&\leq \bigg|\int\varphi \,d\mu_n^{(N)}-\bigg(1-\frac{1}{2^N}\bigg)\int\varphi \,d\mu_+\bigg|+\frac{1}{2^N}\bigg|\int\varphi \,d\mu_+\bigg|\\ &\leq \frac{1}{2^{N-1}}\sup|\varphi|. \end{align*} $$
$$ \begin{align*} \bigg|\int\varphi \,d\mu_n^{(N)}-\int\varphi \,d\mu_+\bigg|&\leq \bigg|\int\varphi \,d\mu_n^{(N)}-\bigg(1-\frac{1}{2^N}\bigg)\int\varphi \,d\mu_+\bigg|+\frac{1}{2^N}\bigg|\int\varphi \,d\mu_+\bigg|\\ &\leq \frac{1}{2^{N-1}}\sup|\varphi|. \end{align*} $$
Since
![]() $\mu _n-\mu _n^{(N)}=\sum \nolimits _{j=N+1}^n\mu _{n,j}$
has mass at most
$\mu _n-\mu _n^{(N)}=\sum \nolimits _{j=N+1}^n\mu _{n,j}$
has mass at most
![]() ${1}/{2^N}$
, we get
${1}/{2^N}$
, we get
 $$ \begin{align*} \bigg|\int\varphi \,d\mu_n-\int\varphi \,d\mu_+\bigg|&\leq \bigg|\int\varphi \,d\mu_n-\int\varphi \,d\mu_n^{(N)}\bigg|+\bigg|\int\varphi \,d\mu_n^{(N)}-\int\varphi \,d\mu_+\bigg|\\ &\leq \frac{3}{2^N}\sup|\varphi|<\varepsilon. \end{align*} $$
$$ \begin{align*} \bigg|\int\varphi \,d\mu_n-\int\varphi \,d\mu_+\bigg|&\leq \bigg|\int\varphi \,d\mu_n-\int\varphi \,d\mu_n^{(N)}\bigg|+\bigg|\int\varphi \,d\mu_n^{(N)}-\int\varphi \,d\mu_+\bigg|\\ &\leq \frac{3}{2^N}\sup|\varphi|<\varepsilon. \end{align*} $$
This proves that for all
![]() $\varphi :\widehat {\mathbb {C}}\to \mathbb {R}$
, we have that
$\varphi :\widehat {\mathbb {C}}\to \mathbb {R}$
, we have that
![]() $\int \varphi \,d\mu _n\to \int \varphi \,d\mu _+$
as
$\int \varphi \,d\mu _n\to \int \varphi \,d\mu _+$
as
![]() $n\to \infty $
and hence
$n\to \infty $
and hence
![]() $\mu _n\to \mu _+$
. Since
$\mu _n\to \mu _+$
. Since
![]() $(1/2^n)(\mathcal {F}_a^n)_*\delta _{z_0}=(1/2^n)\delta _{{f_a}^n(z_0)}+\mu _n$
, we obtain that
$(1/2^n)(\mathcal {F}_a^n)_*\delta _{z_0}=(1/2^n)\delta _{{f_a}^n(z_0)}+\mu _n$
, we obtain that
![]() $(1/2^n)(\mathcal {F}_a^n)_*\delta _{z_0}$
is weakly convergent to
$(1/2^n)(\mathcal {F}_a^n)_*\delta _{z_0}$
is weakly convergent to
![]() $\mu _+$
, as desired.
$\mu _+$
, as desired.
Applying again the push-forward by
![]() $\operatorname {J}_a$
, we get that for every
$\operatorname {J}_a$
, we get that for every
![]() $z_0\notin \mathcal {E}_a$
,
$z_0\notin \mathcal {E}_a$
,
![]() $(1/2^n)(\mathcal {F}_a^n)^*\delta _{z_0}$
is weakly convergent to
$(1/2^n)(\mathcal {F}_a^n)^*\delta _{z_0}$
is weakly convergent to
![]() $\mu _-$
.
$\mu _-$
.
Now, we show the asymptotic equidistribution of periodic points of
![]() $\mathcal {F}_a$
of order n with respect to the probability measure
$\mathcal {F}_a$
of order n with respect to the probability measure
![]() $\tfrac 12(\mu _-+\mu _+)$
.
$\tfrac 12(\mu _-+\mu _+)$
.
Proof of Theorem 1.3.
From Lemma 4.4, we have that all periodic points lie in
![]() ${\Lambda _{a,-}\cup \Lambda _{a,+}}$
and
${\Lambda _{a,-}\cup \Lambda _{a,+}}$
and
Denote this number by
![]() $d_n$
. Since
$d_n$
. Since
![]() $1\in \mathcal {F}_a(1)$
and Lemma 4.4 says
$1\in \mathcal {F}_a(1)$
and Lemma 4.4 says
![]() $\Lambda _{a,-}\cap \Lambda _{a,+}=\lbrace 1\rbrace $
, then
$\Lambda _{a,-}\cap \Lambda _{a,+}=\lbrace 1\rbrace $
, then
Thus,
. Since the conjugacy h between
![]() $f_a$
and the quadratic rational map
$f_a$
and the quadratic rational map
![]() $P_A$
sends
$P_A$
sends
![]() $\Lambda _{a,-}$
onto the filled Julia set
$\Lambda _{a,-}$
onto the filled Julia set
![]() $K_{P_A}$
of
$K_{P_A}$
of
![]() $P_A$
, which contains all periodic points of
$P_A$
, which contains all periodic points of
![]() $P_A$
by Remark 5.1,
$P_A$
by Remark 5.1,
![]() $\operatorname {Per}_n(P_A)=h(\operatorname {Per}_n(\mathcal {F}_a)\cap \Lambda _{a,-})$
and
$\operatorname {Per}_n(P_A)=h(\operatorname {Per}_n(\mathcal {F}_a)\cap \Lambda _{a,-})$
and
as well. We have that
![]() $\lim \nolimits _{n\to \infty }d_n=\infty $
(see in [Reference Ljubich24, p. 363]). Then,
$\lim \nolimits _{n\to \infty }d_n=\infty $
(see in [Reference Ljubich24, p. 363]). Then,
 $$ \begin{align*} \frac{1}{2d_n-1}\sum\limits_{z\in\operatorname{Per}_n(\mathcal{F}_a)\cap\Lambda_{a,-}}\delta_z&= \frac{1}{2d_n-1}\sum\limits_{z\in\operatorname{Per}_n(f_a)}\delta_z\\ &= h^*\bigg(\frac{1}{2d_n-1}\sum\limits_{z\in\operatorname{Per}_n(f_a)}\delta_{h(z)}\bigg)\\ &= h^*\bigg(\frac{d_n}{2d_n-1}\frac{1}{d_n}\sum\limits_{\zeta\in\operatorname{Per}_n(P_A)}\delta_{\zeta}\bigg), \end{align*} $$
$$ \begin{align*} \frac{1}{2d_n-1}\sum\limits_{z\in\operatorname{Per}_n(\mathcal{F}_a)\cap\Lambda_{a,-}}\delta_z&= \frac{1}{2d_n-1}\sum\limits_{z\in\operatorname{Per}_n(f_a)}\delta_z\\ &= h^*\bigg(\frac{1}{2d_n-1}\sum\limits_{z\in\operatorname{Per}_n(f_a)}\delta_{h(z)}\bigg)\\ &= h^*\bigg(\frac{d_n}{2d_n-1}\frac{1}{d_n}\sum\limits_{\zeta\in\operatorname{Per}_n(P_A)}\delta_{\zeta}\bigg), \end{align*} $$
which is weakly convergent to
![]() $\tfrac 12h^*\widetilde {\mu }_A=\tfrac 12\mu _-$
by the corollary to Theorem 3 in [Reference Ljubich24]. Thus,
$\tfrac 12h^*\widetilde {\mu }_A=\tfrac 12\mu _-$
by the corollary to Theorem 3 in [Reference Ljubich24]. Thus,
 $$ \begin{align*} \frac{1}{2d_n-1}\sum\limits_{z\in\operatorname{Per}_n(\mathcal{F}_a)\cap\Lambda_{a,+}}\delta_z= \operatorname{J}_a^*\bigg(\frac{1}{2d_n-1}\sum\limits_{\operatorname{J}_a(z)\in \operatorname{Per}_n(\mathcal{F}_a)\cap\Lambda_{a,-}}\delta_{\operatorname{J}_a(z)}\bigg) \end{align*} $$
$$ \begin{align*} \frac{1}{2d_n-1}\sum\limits_{z\in\operatorname{Per}_n(\mathcal{F}_a)\cap\Lambda_{a,+}}\delta_z= \operatorname{J}_a^*\bigg(\frac{1}{2d_n-1}\sum\limits_{\operatorname{J}_a(z)\in \operatorname{Per}_n(\mathcal{F}_a)\cap\Lambda_{a,-}}\delta_{\operatorname{J}_a(z)}\bigg) \end{align*} $$
is weakly convergent to
![]() $\tfrac 12\operatorname {J}_a^*\mu _-=\tfrac 12\mu _+$
, and
$\tfrac 12\operatorname {J}_a^*\mu _-=\tfrac 12\mu _+$
, and

converges weakly to
![]() $\tfrac 12(\mu _-+\mu _+)$
, as desired.
$\tfrac 12(\mu _-+\mu _+)$
, as desired.
Finally, we proceed to show that the equidistribution still holds when counting with multiplicity. Observe that the only points of
![]() $\Lambda _{a,-}$
that are not in the interior of the topological conjugacy h are
$\Lambda _{a,-}$
that are not in the interior of the topological conjugacy h are
![]() $-$
2 and
$-$
2 and
![]() $1$
, and we have that
$1$
, and we have that
![]() $-$
2 is not a periodic point for
$-$
2 is not a periodic point for
![]() $\mathcal {F}_a$
. We claim that for every
$\mathcal {F}_a$
. We claim that for every
![]() $z_0\in \operatorname {Per}_n({f_a})\setminus \lbrace 1\rbrace $
, we have that
$z_0\in \operatorname {Per}_n({f_a})\setminus \lbrace 1\rbrace $
, we have that
Indeed, the topological conjugacy h sends attracting periodic points to attracting periodic points, so if
![]() $|(f_a^n)'(z_0)|<1$
, then
$|(f_a^n)'(z_0)|<1$
, then
![]() $|(P^n_A)'(h(z_0))|<1$
as well. Thus, both
$|(P^n_A)'(h(z_0))|<1$
as well. Thus, both
![]() $z_0$
and
$z_0$
and
![]() $h(z_0)$
have multiplicity
$h(z_0)$
have multiplicity
![]() $1$
as a periodic point in this case. The same happens for
$1$
as a periodic point in this case. The same happens for
![]() $|(f_a^n)'(z_0)|>1$
. Finally, if
$|(f_a^n)'(z_0)|>1$
. Finally, if
![]() $|(f_a^n)'(z_0)|=|(P^n_A)'(h(z_0))|=1$
, Naishul’s theorem [Reference Naishul27] (later re-proven by Pérez-Marco in [Reference Pérez-Marco28]) shows that
$|(f_a^n)'(z_0)|=|(P^n_A)'(h(z_0))|=1$
, Naishul’s theorem [Reference Naishul27] (later re-proven by Pérez-Marco in [Reference Pérez-Marco28]) shows that
![]() $(f_a^n)'(z_0)=(P^n_A)'(h(z_0))$
. Moreover, attracting directions are preserved under topological conjugacy, so the parabolic fixed point
$(f_a^n)'(z_0)=(P^n_A)'(h(z_0))$
. Moreover, attracting directions are preserved under topological conjugacy, so the parabolic fixed point
![]() $z_0$
of
$z_0$
of
![]() $\mathcal {F}_a$
and the parabolic fixed point
$\mathcal {F}_a$
and the parabolic fixed point
![]() $h(z_0)$
of
$h(z_0)$
of
![]() $P_A$
have the same number of attracting directions. Therefore, both
$P_A$
have the same number of attracting directions. Therefore, both
![]() $z_0$
and
$z_0$
and
![]() $h(z_0)$
have the same multiplicity as periodic points of order n of
$h(z_0)$
have the same multiplicity as periodic points of order n of
![]() $f_a$
and
$f_a$
and
![]() $P_A$
, respectively. Therefore,
$P_A$
, respectively. Therefore,

From Lemma 4.4 part
![]() $(2)$
and given that
$(2)$
and given that
![]() $\operatorname {J}_a$
is a Mobius transformation, we have that
$\operatorname {J}_a$
is a Mobius transformation, we have that

as well.
Since the multiplicity of a periodic point is the multiplicity as a periodic point of its minimal period and since
![]() $\phi ^{-1}(0)=\infty $
, we have that
$\phi ^{-1}(0)=\infty $
, we have that

Similarly, from the equations for
![]() $g^{\psi }$
listed in Remark 3.5, we have that
$g^{\psi }$
listed in Remark 3.5, we have that

In [Reference Bullett and Lomonaco5, Corollary 4.3], the authors showed that for
![]() $a=7$
, the member of the family of quadratic rational maps
$a=7$
, the member of the family of quadratic rational maps
that is conjugate to
![]() $f_a$
is
$f_a$
is
![]() $P_0$
. Therefore, for all
$P_0$
. Therefore, for all
![]() $a\in \mathbb {C}\setminus \lbrace 1\rbrace $
,
$a\in \mathbb {C}\setminus \lbrace 1\rbrace $
,
![]() $|a-4|\leq 3$
,
$|a-4|\leq 3$
,

and we have that

which also converges weakly to
![]() $\mu _-$
by [Reference Ljubich24, Theorem 3]. Using that
$\mu _-$
by [Reference Ljubich24, Theorem 3]. Using that
![]() $\operatorname {J}_a$
preserves multiplicities and that
$\operatorname {J}_a$
preserves multiplicities and that
![]() $\operatorname {J}_a^*\mu _-=\mu _+$
, we have that
$\operatorname {J}_a^*\mu _-=\mu _+$
, we have that

is weakly convergent to
![]() $\mu _+$
. Since
$\mu _+$
. Since
has total mass
![]() ${1}/{2^n}$
and
${1}/{2^n}$
and
is a disjoint union, then

is weakly convergent to
![]() $\tfrac 12(\mu _-+\mu _+)$
.
$\tfrac 12(\mu _-+\mu _+)$
.
In what follows, we will introduce terminology and prove Theorem 1.4.
Definition 5.3. A holomorphic correspondence F with graph
![]() $\Gamma $
is said to be postcritically finite if for all
$\Gamma $
is said to be postcritically finite if for all
![]() $w\in B_2(\Gamma )$
, there exist
$w\in B_2(\Gamma )$
, there exist
![]() $0\leq m<n$
so that
$0\leq m<n$
so that
Equivalently, for every
![]() $w\in B_2(\Gamma )$
, there exists
$w\in B_2(\Gamma )$
, there exists
![]() $m\geq 0$
and
$m\geq 0$
and
![]() $z\in F^m(w)$
so that
$z\in F^m(w)$
so that
![]() ${z\in \operatorname {Per}_n(F)}$
for some
${z\in \operatorname {Per}_n(F)}$
for some
![]() $n\geq 1$
. This definition generalizes that of postcritically finite rational maps. Indeed, if F is a rational map that is postcritically finite as a correspondence, then we have that every
$n\geq 1$
. This definition generalizes that of postcritically finite rational maps. Indeed, if F is a rational map that is postcritically finite as a correspondence, then we have that every
![]() $w\in B_2(\Gamma )$
is pre-periodic. Since
$w\in B_2(\Gamma )$
is pre-periodic. Since
![]() $B_2(\Gamma )=F(\operatorname {CritPt}(F))$
, then every critical point is pre-periodic as well. Hence, F is postcritically finite as a rational map.
$B_2(\Gamma )=F(\operatorname {CritPt}(F))$
, then every critical point is pre-periodic as well. Hence, F is postcritically finite as a rational map.
If F is a holomorphic correspondence and
![]() $z_0\in \operatorname {Per}_n(F)$
, there exists a cycle
$z_0\in \operatorname {Per}_n(F)$
, there exists a cycle
so that
![]() $z_i\in F(z_{i-1})$
and
$z_i\in F(z_{i-1})$
and
![]() $z_0\in F(z_{n-1})$
.
$z_0\in F(z_{n-1})$
.
Definition 5.4. We say that a holomorphic correspondence with graph
![]() $\Gamma $
is superstable if there exists
$\Gamma $
is superstable if there exists
![]() $\alpha \in A_2(\Gamma )$
and a cycle in equation (18) satisfying that
$\alpha \in A_2(\Gamma )$
and a cycle in equation (18) satisfying that
![]() $z_0=\pi _1(\alpha )$
and
$z_0=\pi _1(\alpha )$
and
![]() ${z_1=\pi _2(\alpha )}$
.
${z_1=\pi _2(\alpha )}$
.
Observe that if F is a rational map, then
![]() $\pi _1(\alpha )$
corresponds to a critical point and
$\pi _1(\alpha )$
corresponds to a critical point and
![]() $\pi _2(\alpha )$
corresponds to its critical value. Therefore, the definition of superstable correspondences reduces to F having a superstable cycle, meaning a cycle containing a critical point.
$\pi _2(\alpha )$
corresponds to its critical value. Therefore, the definition of superstable correspondences reduces to F having a superstable cycle, meaning a cycle containing a critical point.
In the context of the family
![]() $\lbrace \mathcal {F}_a\rbrace _{a\in \mathcal {K}}$
, Proposition 2.4 says that
$\lbrace \mathcal {F}_a\rbrace _{a\in \mathcal {K}}$
, Proposition 2.4 says that
 $$ \begin{align*}B_2(\Gamma_a)=\bigg\lbrace \frac{a+1}{2},\frac{4a+2}{a+5},\frac{2}{3-a}\bigg\rbrace.\end{align*} $$
$$ \begin{align*}B_2(\Gamma_a)=\bigg\lbrace \frac{a+1}{2},\frac{4a+2}{a+5},\frac{2}{3-a}\bigg\rbrace.\end{align*} $$
Observe that
![]() $({a+1})/{2}=\operatorname {J}_a(\infty )\notin \Lambda _{a,-}\cup \Lambda _{a,+}$
. Indeed, since
$({a+1})/{2}=\operatorname {J}_a(\infty )\notin \Lambda _{a,-}\cup \Lambda _{a,+}$
. Indeed, since
![]() $\infty $
is fixed by
$\infty $
is fixed by
![]() $\operatorname {Cov^Q_0}$
and
$\operatorname {Cov^Q_0}$
and
![]() $(\Delta ^{\prime }_{\operatorname {Cov^Q_0}},\Delta ^{\prime }_{\operatorname {J}_a})$
is a Klein combination pair, then
$(\Delta ^{\prime }_{\operatorname {Cov^Q_0}},\Delta ^{\prime }_{\operatorname {J}_a})$
is a Klein combination pair, then
![]() $\infty \in (\widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {Cov^Q_0}})\setminus \lbrace 1\rbrace \subset \Delta ^{\prime }_{\operatorname {J}_a}$
, so
$\infty \in (\widehat {\mathbb {C}}\setminus \Delta ^{\prime }_{\operatorname {Cov^Q_0}})\setminus \lbrace 1\rbrace \subset \Delta ^{\prime }_{\operatorname {J}_a}$
, so
![]() ${\operatorname {J}_a(\infty )\notin \Lambda _{a,-}\subset \overline {\Delta ^{\prime }_{\operatorname {J}_a}}}$
. On the other hand,
${\operatorname {J}_a(\infty )\notin \Lambda _{a,-}\subset \overline {\Delta ^{\prime }_{\operatorname {J}_a}}}$
. On the other hand,
![]() $\mathcal {F}_a^{-1}(\operatorname {J}_a(\infty ))=\lbrace \infty \rbrace $
does not intersect
$\mathcal {F}_a^{-1}(\operatorname {J}_a(\infty ))=\lbrace \infty \rbrace $
does not intersect
![]() $\Lambda _{a,+}$
, so
$\Lambda _{a,+}$
, so
![]() ${\operatorname {J}_a(\infty )\notin \Lambda _{a,+}}$
. By Lemma (4.4),
${\operatorname {J}_a(\infty )\notin \Lambda _{a,+}}$
. By Lemma (4.4),
![]() $({a+1})/{2}$
cannot satisfy equation (17). Therefore, there are no parameters
$({a+1})/{2}$
cannot satisfy equation (17). Therefore, there are no parameters
![]() $a\in \mathcal {K}$
for which
$a\in \mathcal {K}$
for which
![]() $\mathcal {F}_a$
is postcritically finite.
$\mathcal {F}_a$
is postcritically finite.
However,
![]() and
and
![]() , so
, so
![]() $({4a+2})/({a+5})$
is not periodic. Therefore,
$({4a+2})/({a+5})$
is not periodic. Therefore,
![]() $\mathcal {F}_a$
is superstable if and only if
$\mathcal {F}_a$
is superstable if and only if
![]() ${2}/({3-a})$
is periodic. Since
${2}/({3-a})$
is periodic. Since
![]() $\mathcal {F}_a^{-1}({2}/({3-a}))=\lbrace -1\rbrace $
and
$\mathcal {F}_a^{-1}({2}/({3-a}))=\lbrace -1\rbrace $
and
![]() $\mathcal {F}_a^{-1}=f_a^{-1}$
, then
$\mathcal {F}_a^{-1}=f_a^{-1}$
, then
![]() $\mathcal {F}_a$
is superstable if and only if
$\mathcal {F}_a$
is superstable if and only if
![]() $-1$
is a critical point of
$-1$
is a critical point of
![]() $f_a$
that is periodic. We say that the parameter
$f_a$
that is periodic. We say that the parameter
![]() $a\in \mathcal {K}$
is superstable whenever
$a\in \mathcal {K}$
is superstable whenever
![]() $\mathcal {F}_a$
is superstable.
$\mathcal {F}_a$
is superstable.
We consider the quadratic family
and let
![]() be the set of superstable parameters of order n. Note that
be the set of superstable parameters of order n. Note that
![]() $\hat {P}_n$
has
$\hat {P}_n$
has
![]() $2^{n-1}$
points, counted with multiplicity, and that it is contained in the Mandelbrot set
$2^{n-1}$
points, counted with multiplicity, and that it is contained in the Mandelbrot set
![]() $\mathcal {M}$
. Levin proved in [Reference Levin23] that
$\mathcal {M}$
. Levin proved in [Reference Levin23] that
 $$ \begin{align*}\lim\limits_{n\to\infty}\frac{1}{2^{n-1}}\sum\limits_{c\in\hat{P}_n}\delta_{c}\end{align*} $$
$$ \begin{align*}\lim\limits_{n\to\infty}\frac{1}{2^{n-1}}\sum\limits_{c\in\hat{P}_n}\delta_{c}\end{align*} $$
converges to a measure
![]() $m_{\operatorname {BIF}}$
on
$m_{\operatorname {BIF}}$
on
![]() $\mathcal {M}$
, which we call the bifurcation measure.
$\mathcal {M}$
, which we call the bifurcation measure.
Let
![]() $\mathcal {M}_{\Gamma }$
denote the connectedness locus of the family
$\mathcal {M}_{\Gamma }$
denote the connectedness locus of the family
![]() $\lbrace \mathcal {F}_a\rbrace _{a\in \mathcal {K}}$
and
$\lbrace \mathcal {F}_a\rbrace _{a\in \mathcal {K}}$
and
![]() $\mathcal {M}_1$
denote the parabolic Mandelbrot set. The conjugacy shown in [Reference Bullett and Lomonaco4] between
$\mathcal {M}_1$
denote the parabolic Mandelbrot set. The conjugacy shown in [Reference Bullett and Lomonaco4] between
![]() $f_a$
and
$f_a$
and
![]() $P_A$
induces a map
$P_A$
induces a map
![]() $a\mapsto 1-A^2$
from
$a\mapsto 1-A^2$
from
![]() $\mathcal {M}_{\Gamma }$
and
$\mathcal {M}_{\Gamma }$
and
![]() $\mathcal {M}_1$
. From [Reference Bullett and Lomonaco5, Main Theorem], that map is a homeomorphism. On the other hand, [Reference Petersen and Roesch29, Main Theorem] says that
$\mathcal {M}_1$
. From [Reference Bullett and Lomonaco5, Main Theorem], that map is a homeomorphism. On the other hand, [Reference Petersen and Roesch29, Main Theorem] says that
![]() $\mathcal {M}_1$
is homeomorphic to
$\mathcal {M}_1$
is homeomorphic to
![]() $\mathcal {M}$
. Moreover, both homeomorphisms constructed preserve the type of dynamics associated to the parameter (see [Reference Petersen and Roesch29, §1]). Therefore, there is a homeomorphism
$\mathcal {M}$
. Moreover, both homeomorphisms constructed preserve the type of dynamics associated to the parameter (see [Reference Petersen and Roesch29, §1]). Therefore, there is a homeomorphism
![]() $\Psi :\mathcal {M}\to \mathcal {M}_{\Gamma }$
that gives a one-to-one correspondence between superstable parameters of
$\Psi :\mathcal {M}\to \mathcal {M}_{\Gamma }$
that gives a one-to-one correspondence between superstable parameters of
![]() $\mathcal {M}_{\Gamma }$
and superstable parameters of
$\mathcal {M}_{\Gamma }$
and superstable parameters of
![]() $\mathcal {M}$
. Pushing the bifurcation measure forward through
$\mathcal {M}$
. Pushing the bifurcation measure forward through
![]() $\Psi $
, and writing
$\Psi $
, and writing
we obtain the statement in Theorem 1.4.
Acknowledgements
The author would like to thank Shaun Bullett and Luna Lomonaco for a useful conversation in Santiago de Chile, and especially thank Juan Rivera-Letelier for his great patience and guidance.