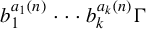1 Introduction and main results
1.1 History and main goals
In recent years, there has been an active interest in determining the limiting behaviour of the multiple ergodic averages
 $$ \begin{align} \frac{1}{N}\sum_{n=1}^{N} f_1(T^{a_1(n)}x)\cdots f_k(T^{a_k(n)}x) \end{align} $$
$$ \begin{align} \frac{1}{N}\sum_{n=1}^{N} f_1(T^{a_1(n)}x)\cdots f_k(T^{a_k(n)}x) \end{align} $$
for various sequences
![]() $a_1(n),\ldots ,a_k(n)$
of integers, where T is an invertible measure-preserving transformation acting on a probability space
$a_1(n),\ldots ,a_k(n)$
of integers, where T is an invertible measure-preserving transformation acting on a probability space
![]() $(X,\mathcal {X},\mu )$
and
$(X,\mathcal {X},\mu )$
and
![]() $f_1,\ldots ,f_k$
are functions in
$f_1,\ldots ,f_k$
are functions in
![]() $L^{\infty }(\mu )$
. Through the breakthrough work of Furstenberg [Reference Furstenberg8], which delivered a new proof of Szemerédi’s theorem using tools from ergodic theory, it has been apparent that the analysis of the averages in equation (1) has noteworthy applications to number theory and combinatorics. In particular, we now have substantial generalizations of Szemerédi’s theorem, some of which have not been demonstrated with approaches other than the use of ergodic theory.
$L^{\infty }(\mu )$
. Through the breakthrough work of Furstenberg [Reference Furstenberg8], which delivered a new proof of Szemerédi’s theorem using tools from ergodic theory, it has been apparent that the analysis of the averages in equation (1) has noteworthy applications to number theory and combinatorics. In particular, we now have substantial generalizations of Szemerédi’s theorem, some of which have not been demonstrated with approaches other than the use of ergodic theory.
An integral tool in verifying convergence of the averages in equation (1) is the structure theorem of Host and Kra [Reference Host and Kra11], which in multiple cases reduces the above problem to studying rotations on particular spaces with algebraic structure, which are called nilmanifolds (see [Reference Host and Kra12] for a full presentation of the theory). A nilmanifold is a homogeneous space
![]() $X=G/\Gamma $
, where G is a nilpotent Lie group and
$X=G/\Gamma $
, where G is a nilpotent Lie group and
![]() $\Gamma $
is a discrete cocompact subgroup. The study of nilmanifolds is essential due to its ties to ergodic theory mentioned above, as well as the numerous applications to combinatorics and number theory.
$\Gamma $
is a discrete cocompact subgroup. The study of nilmanifolds is essential due to its ties to ergodic theory mentioned above, as well as the numerous applications to combinatorics and number theory.
In this article, our central problem is the study of the distribution of orbits in a nilmanifold along sequences that arise from smooth functions with polynomial growth. We suppose that our functions are elements of a Hardy field (for the definition of a Hardy field, we direct the reader to §2). The benefit of working within a Hardy field is that certain ‘regularity’ properties of the derivatives of a function, which are vital in several parts of our proofs, can be extrapolated from a simple growth condition on the initial function. For instance, a condition like equation (P) below imposes multiple pleasant properties on the derivatives of a function in
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
The field of logarithmico-exponential functions is the prototypical example of a Hardy field. It is defined as the collection of functions formed by a finite combination of the operations
![]() $+,-,\cdot ,\div ,\ \exp $
,
$+,-,\cdot ,\div ,\ \exp $
,
![]() $\log $
and composition of functions acting on a real variable t (which takes values on some half-line
$\log $
and composition of functions acting on a real variable t (which takes values on some half-line
![]() $[x,+\infty )$
) and real constants. The fact that it is a Hardy field was established in [Reference Hardy10]. Our results are most interesting for the Hardy field
$[x,+\infty )$
) and real constants. The fact that it is a Hardy field was established in [Reference Hardy10]. Our results are most interesting for the Hardy field
![]() $\mathcal {LE}$
and one can keep this particular case in mind throughout the article. In addition, we refer the reader to Appendix B for the definition and properties of nilmanifolds, which appear in the subsequent discussion and the main theorems.
$\mathcal {LE}$
and one can keep this particular case in mind throughout the article. In addition, we refer the reader to Appendix B for the definition and properties of nilmanifolds, which appear in the subsequent discussion and the main theorems.
Due to its connections to ergodic theory and combinatorics, the investigation of equidistribution properties along Hardy sequences has been carried out several times throughout the literature. First of all, we recall a fundamental result concerning the equidistribution of Hardy sequences, which corresponds to the basic case when the underlying nilmanifold is a finite-dimensional torus. In particular, we restate here [Reference Boshernitzan2, Theorem 1.3].
Theorem A. (Boshernitzan)
Let the function
![]() $a \in \mathcal {H}$
have polynomial growth. Then, the sequence
$a \in \mathcal {H}$
have polynomial growth. Then, the sequence
![]() $a(n)$
is equidistributed
$a(n)$
is equidistributed
![]() $\mod\! 1$
if and only if
$\mod\! 1$
if and only if
Applying Weyl’s equidistribution theorem and the previous result, we can effortlessly show that if the functions
![]() $a_1,\ldots ,a_k$
have polynomial growth and each non-trivial linear combination of them stays logarithmically away from real multiples of integer polynomials, then the sequence
$a_1,\ldots ,a_k$
have polynomial growth and each non-trivial linear combination of them stays logarithmically away from real multiples of integer polynomials, then the sequence
![]() $(c_1a_1(n),\ldots ,c_ka_k(n))$
is equidistributed on
$(c_1a_1(n),\ldots ,c_ka_k(n))$
is equidistributed on
![]() $\mathbb {T}^k$
for all non-zero real numbers
$\mathbb {T}^k$
for all non-zero real numbers
![]() $c_1,\ldots ,c_k$
. Practically, Theorem A can be used to examine orbits on
$c_1,\ldots ,c_k$
. Practically, Theorem A can be used to examine orbits on
![]() $\mathbb {T}^k$
along the sequences
$\mathbb {T}^k$
along the sequences
![]() $a_1(n),\ldots , a_k(n)$
on
$a_1(n),\ldots , a_k(n)$
on
![]() $\mathbb {T}^k$
, answering our problem in the case when the nilmanifold X is any finite-dimensional torus (the abelian case). Another corollary of Theorem A is that if
$\mathbb {T}^k$
, answering our problem in the case when the nilmanifold X is any finite-dimensional torus (the abelian case). Another corollary of Theorem A is that if
![]() $a(t)\in \mathcal {H}$
stays logarithmically away from real multiples of integer polynomials, then the sequence
$a(t)\in \mathcal {H}$
stays logarithmically away from real multiples of integer polynomials, then the sequence
![]() $ \left \lfloor {a(n)} \right \rfloor a$
is equidistributed on
$ \left \lfloor {a(n)} \right \rfloor a$
is equidistributed on
![]() $\mathbb {T}$
for all irrational
$\mathbb {T}$
for all irrational
![]() $a\in (0,1)$
. This phenomenon (namely, that equidistribution properties of
$a\in (0,1)$
. This phenomenon (namely, that equidistribution properties of
![]() $a(n)$
yield information for the equidistribution properties of
$a(n)$
yield information for the equidistribution properties of
![]() $ \left \lfloor {a(n)} \right \rfloor $
) will be present throughout the article, so the reader can view statements involving
$ \left \lfloor {a(n)} \right \rfloor $
) will be present throughout the article, so the reader can view statements involving
![]() $a(n)$
in place of
$a(n)$
in place of
![]() $ \left \lfloor {a(n)} \right \rfloor $
as being morally the same.
$ \left \lfloor {a(n)} \right \rfloor $
as being morally the same.
Suppose now that we are given a nilmanifold
![]() $X=G/\Gamma $
(for the definitions of all terms below, see Appendix B) and assume that the group G is connected and simply connected. We are interested in the behaviour of the sequence
$X=G/\Gamma $
(for the definitions of all terms below, see Appendix B) and assume that the group G is connected and simply connected. We are interested in the behaviour of the sequence
where
![]() $b_1,\ldots ,b_k$
are elements of the group G and
$b_1,\ldots ,b_k$
are elements of the group G and
![]() $a_1,\ldots ,a_k$
are Hardy field functions. Notice that this is a sequence on the product nilmanifold
$a_1,\ldots ,a_k$
are Hardy field functions. Notice that this is a sequence on the product nilmanifold
![]() $X^k$
. The most fundamental equidistribution result is due to Leibman, who showed that if the functions
$X^k$
. The most fundamental equidistribution result is due to Leibman, who showed that if the functions
![]() $a_1,\ldots a_k$
are integer polynomials, then we have equidistribution on a ‘subspace’ of X (called a subnilmanifold), as long as we restrict the values of n to appropriate arithmetic progressions.
$a_1,\ldots a_k$
are integer polynomials, then we have equidistribution on a ‘subspace’ of X (called a subnilmanifold), as long as we restrict the values of n to appropriate arithmetic progressions.
More specifically, we present the following theorem [Reference Leibman13, Theorem B], an application of which (on the nilmanifold
![]() $X^k$
) implies the claim in the previous paragraph.
$X^k$
) implies the claim in the previous paragraph.
Theorem B. (Leibman)
Let
![]() $X=G/\Gamma $
be a nilmanifold and
$X=G/\Gamma $
be a nilmanifold and
![]() $x\in X$
. Consider the sequence
$x\in X$
. Consider the sequence
in G, where
![]() $b_1,\ldots ,b_k\in G$
and
$b_1,\ldots ,b_k\in G$
and
![]() $p_1,\ldots , p_k$
are polynomials with integer coefficients. Then, there exists
$p_1,\ldots , p_k$
are polynomials with integer coefficients. Then, there exists
![]() $Q\in \mathbb {N}$
, a closed, connected and rational subgroup H of G and points
$Q\in \mathbb {N}$
, a closed, connected and rational subgroup H of G and points
![]() $x_0,\ldots , x_{Q-1}\in X$
, such that for every
$x_0,\ldots , x_{Q-1}\in X$
, such that for every
![]() $r\in \{0,\ldots ,Q-1\}$
, the sequence
$r\in \{0,\ldots ,Q-1\}$
, the sequence
![]() $g(Qn+r)x$
is equidistributed on the subnilmanifold
$g(Qn+r)x$
is equidistributed on the subnilmanifold
![]() $Hx_r$
.
$Hx_r$
.
A noteworthy corollary of the previous theorem is that if
![]() $F: X\to \mathbb {C}$
is a continuous function, then the averages
$F: X\to \mathbb {C}$
is a continuous function, then the averages
 $$ \begin{align*} \frac{1}{N}\sum_{n=1}^{N} F(g(n)x) \end{align*} $$
$$ \begin{align*} \frac{1}{N}\sum_{n=1}^{N} F(g(n)x) \end{align*} $$
converge pointwise for all
![]() $x\in X$
. This can be used in conjunction with the Host–Kra structure theory (see Theorem E in §2) to infer that the averages in equation (1) converge in norm, when the sequences
$x\in X$
. This can be used in conjunction with the Host–Kra structure theory (see Theorem E in §2) to infer that the averages in equation (1) converge in norm, when the sequences
![]() $a_1(n),\ldots ,a_k(n)$
are integer polynomial sequences. In addition, we deduce (as a corollary of [Reference Leibman13, Theorem C] in the same paper) that if G is connected, the equidistribution of the sequence
$a_1(n),\ldots ,a_k(n)$
are integer polynomial sequences. In addition, we deduce (as a corollary of [Reference Leibman13, Theorem C] in the same paper) that if G is connected, the equidistribution of the sequence
![]() $g(n)\Gamma $
is controlled by the projection of
$g(n)\Gamma $
is controlled by the projection of
![]() $g(n)\Gamma $
on the ‘abelianization’
$g(n)\Gamma $
on the ‘abelianization’
![]() $G/[G, G]\Gamma $
of
$G/[G, G]\Gamma $
of
![]() $G/\Gamma $
, which is a finite-dimensional torus called the horizontal torus of X.
$G/\Gamma $
, which is a finite-dimensional torus called the horizontal torus of X.
A major improvement of the above theorem was established by Green and Tao in [Reference Green and Tao9], who characterized the behaviour of polynomial orbits on nilmanifolds in quantitative language. (While their theorem was established under the stronger hypothesis that the underlying Lie group G is connected and simply connected, one can typically reduce to this case in many applications.) This theorem has notable applications in number theory and will be undoubtedly vital in this paper. Like Leibman’s theorem in [Reference Leibman13] that we mentioned above briefly, this theorem highlights the relation of the equidistribution properties of a polynomial sequence (see Definition B.3) on a nilmanifold with its projection to the horizontal torus. Since there are many technical terms that are required to state this theorem, we have presented its statement in Appendix B along with a sample corollary when the nilmanifold is a torus, as well as all of the required background on the quantitative equidistribution theory on nilmanifolds.
Now, let us consider the more general case when the sequences
![]() $a_1(n),\ldots , a_k(n)$
appearing in equation (2) are not just integer polynomials, but functions that belong to a Hardy field
$a_1(n),\ldots , a_k(n)$
appearing in equation (2) are not just integer polynomials, but functions that belong to a Hardy field
![]() $\mathcal {H}$
. In the case
$\mathcal {H}$
. In the case
![]() $k=1$
, Frantzikinakis established [Reference Frantzikinakis4] that if the function
$k=1$
, Frantzikinakis established [Reference Frantzikinakis4] that if the function
![]() $a(t)$
satisfies
$a(t)$
satisfies
then the sequence
![]() $b^{ \left \lfloor {a_1(n)} \right \rfloor }x$
is equidistributed on the orbit
$b^{ \left \lfloor {a_1(n)} \right \rfloor }x$
is equidistributed on the orbit
![]() $Y=\overline {\{b^nx\colon n\in \mathbb {N}\}}$
of b for any
$Y=\overline {\{b^nx\colon n\in \mathbb {N}\}}$
of b for any
![]() $b\in G$
and
$b\in G$
and
![]() $x\in X$
. In the case of general k, he also established the following theorem in the same paper.
$x\in X$
. In the case of general k, he also established the following theorem in the same paper.
Theorem C. (Frantzikinakis [Reference Frantzikinakis4, Theorem 1.3])
Let
![]() $a_1,\ldots , a_k$
be functions of polynomial growth that belong to a Hardy field
$a_1,\ldots , a_k$
be functions of polynomial growth that belong to a Hardy field
![]() $\mathcal {H}$
, such that they have pairwise distinct growth rates and satisfy
$\mathcal {H}$
, such that they have pairwise distinct growth rates and satisfy
for some
![]() $k_i\in \mathbb {N}$
. Then, for any nilmanifold
$k_i\in \mathbb {N}$
. Then, for any nilmanifold
![]() $X=G/\Gamma $
and
$X=G/\Gamma $
and
![]() $b_1,\ldots , b_k\in G$
, the sequence
$b_1,\ldots , b_k\in G$
, the sequence
is equidistributed on
![]() $\overline {(b_1^{n}x_1)}_{n\in \mathbb {N}}\times \cdots \times \overline {(b_k^nx_k)}_{n\in \mathbb {N}\,}$
for all
$\overline {(b_1^{n}x_1)}_{n\in \mathbb {N}}\times \cdots \times \overline {(b_k^nx_k)}_{n\in \mathbb {N}\,}$
for all
![]() $x_1,\ldots , x_k\in X$
.
$x_1,\ldots , x_k\in X$
.
In the same paper, Frantzikinakis conjectured that if the linear combinations of the functions
![]() $a_1,\ldots ,a_k$
stay logarithmically away from real multiples of integer polynomials, then the sequence in equation (5) is equidistributed on
$a_1,\ldots ,a_k$
stay logarithmically away from real multiples of integer polynomials, then the sequence in equation (5) is equidistributed on
![]() $\overline {(b_1^{n}x_1)_{n\in \mathbb {N}}}\times \cdots \times \overline {(b_k^nx_k)_{n\in \mathbb {N}}}$
. More specifically, we have the following conjecture.
$\overline {(b_1^{n}x_1)_{n\in \mathbb {N}}}\times \cdots \times \overline {(b_k^nx_k)_{n\in \mathbb {N}}}$
. More specifically, we have the following conjecture.
Conjecture 1. [Reference Frantzikinakis4]
Let
![]() $a_1,\ldots , a_k$
be functions in a Hardy field
$a_1,\ldots , a_k$
be functions in a Hardy field
![]() $\mathcal {H}$
with polynomial growth and such that every non-trivial linear combination
$\mathcal {H}$
with polynomial growth and such that every non-trivial linear combination
![]() $a(t)$
of them satisfies
$a(t)$
of them satisfies
Then, for any nilmanifold
![]() $X=G/\Gamma ,\ b_i\in G$
and
$X=G/\Gamma ,\ b_i\in G$
and
![]() $x_i\in X$
, the sequence
$x_i\in X$
, the sequence
is equidistributed on
![]() $\overline {(b_1^{n}x_1)}_{n\in \mathbb {N}}\times \cdots \times \overline {(b_k^nx_k)}_{n\in \mathbb {N}}$
.
$\overline {(b_1^{n}x_1)}_{n\in \mathbb {N}}\times \cdots \times \overline {(b_k^nx_k)}_{n\in \mathbb {N}}$
.
Recently, Richter established the following equidistribution theorem. We present here a special case of that result, where we assume that the underlying Lie group G is connected and simply connected so that the elements
![]() $b^s$
are defined for any
$b^s$
are defined for any
![]() $b\in G$
and
$b\in G$
and
![]() $s\in \mathbb {R}$
(see also the first paragraph of §B.2 for a more thorough explanation). We also define
$s\in \mathbb {R}$
(see also the first paragraph of §B.2 for a more thorough explanation). We also define
Theorem D. (Richter [Reference Richter17, Theorem B])
Let
![]() $X=G/\Gamma $
be a nilmanifold with G connected and simply connected, and let
$X=G/\Gamma $
be a nilmanifold with G connected and simply connected, and let
![]() $a_1,\ldots , a_k$
be functions in a Hardy field
$a_1,\ldots , a_k$
be functions in a Hardy field
![]() $\mathcal {H}$
, such that for any function
$\mathcal {H}$
, such that for any function
![]() $a\in \nabla -\text {span}\{a_1,\ldots ,a_k\}$
, we have that
$a\in \nabla -\text {span}\{a_1,\ldots ,a_k\}$
, we have that
for any polynomial
![]() $p(t)\in \mathbb {R}[t]$
. Consider any commuting elements
$p(t)\in \mathbb {R}[t]$
. Consider any commuting elements
![]() $b_1,\ldots ,b_k\in G$
and define the sequence
$b_1,\ldots ,b_k\in G$
and define the sequence
Then, there exists a closed, connected and rational subgroup H of G, and points
![]() $x_0,\ldots , x_{Q-1}$
in X, such that the sequence
$x_0,\ldots , x_{Q-1}$
in X, such that the sequence
![]() $v(Qn+r)\Gamma $
is equidistributed on the subnilmanifold
$v(Qn+r)\Gamma $
is equidistributed on the subnilmanifold
![]() $Hx_r$
of X for all
$Hx_r$
of X for all
![]() $r\in \{0,\ldots , Q-1\}$
.
$r\in \{0,\ldots , Q-1\}$
.
The hypothesis that
![]() $b_1,\ldots , b_k$
are commuting is harmless in problems regarding the convergence of ergodic averages or in applications to combinatorics. Furthermore, while in this setting we have the sequences
$b_1,\ldots , b_k$
are commuting is harmless in problems regarding the convergence of ergodic averages or in applications to combinatorics. Furthermore, while in this setting we have the sequences
![]() $a_i(n)$
instead of
$a_i(n)$
instead of
![]() $ \left \lfloor {a_i(n)} \right \rfloor $
in the exponents, the statement above actually implies an equidistribution theorem for the sequences
$ \left \lfloor {a_i(n)} \right \rfloor $
in the exponents, the statement above actually implies an equidistribution theorem for the sequences
![]() $ \left \lfloor {a_i(n)} \right \rfloor $
. We remark that the results in [Reference Richter17] are generalized to equidistribution results with respect to (weaker) averaging schemes other than Cesáro averages. Under those averaging schemes, the assumptions on the functions
$ \left \lfloor {a_i(n)} \right \rfloor $
. We remark that the results in [Reference Richter17] are generalized to equidistribution results with respect to (weaker) averaging schemes other than Cesáro averages. Under those averaging schemes, the assumptions on the functions
![]() $a_1,\ldots , a_k$
can be weakened significantly (however, our results deal only with Cesáro averages). In the follow-up paper [Reference Bergelson, Moreira and Richter1], Bergelson, Moreira and Richter employed the above equidistribution results to obtain convergence results for multiple ergodic averages and combinatorial applications for Hardy field sequences.
$a_1,\ldots , a_k$
can be weakened significantly (however, our results deal only with Cesáro averages). In the follow-up paper [Reference Bergelson, Moreira and Richter1], Bergelson, Moreira and Richter employed the above equidistribution results to obtain convergence results for multiple ergodic averages and combinatorial applications for Hardy field sequences.
1.2 Main results
To state our results, we will assume that we have a fixed Hardy field
![]() $\mathcal {H}$
, and the only extra hypothesis we require is that it includes the polynomial functions (this is a very mild restriction). Removing this restriction may be possible, though this would certainly complicate our arguments or the notation in the proofs. Unless noted otherwise, our theorems below apply to any such Hardy field. An exception is made only for Theorem 1.3 (we shall reiterate these assumptions in the main theorems).
$\mathcal {H}$
, and the only extra hypothesis we require is that it includes the polynomial functions (this is a very mild restriction). Removing this restriction may be possible, though this would certainly complicate our arguments or the notation in the proofs. Unless noted otherwise, our theorems below apply to any such Hardy field. An exception is made only for Theorem 1.3 (we shall reiterate these assumptions in the main theorems).
For a given set of functions
![]() $a_1,\ldots ,a_k$
in our Hardy field
$a_1,\ldots ,a_k$
in our Hardy field
![]() $\mathcal {H}$
, we use the notation
$\mathcal {H}$
, we use the notation
to refer to the collection of functions in
![]() $\mathcal {H}$
that are non-trivial linear combinations of the functions
$\mathcal {H}$
that are non-trivial linear combinations of the functions
![]() $a_1(t),\ldots ,a_k(t)$
. The nilmanifolds
$a_1(t),\ldots ,a_k(t)$
. The nilmanifolds
![]() $\overline {(b^{\mathbb {R}}x)}$
and
$\overline {(b^{\mathbb {R}}x)}$
and
![]() $\overline {(b^{\mathbb {N}}x)}$
are defined in §B.2.
$\overline {(b^{\mathbb {N}}x)}$
are defined in §B.2.
Theorem 1.1. Let
![]() $\mathcal {H}$
be a Hardy field containing the polynomial functions. Let
$\mathcal {H}$
be a Hardy field containing the polynomial functions. Let
![]() $a_1,\ldots ,a_k$
be functions in
$a_1,\ldots ,a_k$
be functions in
![]() $\mathcal {H}$
that have polynomial growth. Assume that there exists an
$\mathcal {H}$
that have polynomial growth. Assume that there exists an
![]() $\varepsilon>0$
(the value of
$\varepsilon>0$
(the value of
![]() $\varepsilon $
depends only on the initial collection
$\varepsilon $
depends only on the initial collection
![]() $\{a_1,\ldots ,a_k\}$
), such that every function
$\{a_1,\ldots ,a_k\}$
), such that every function
![]() $a\in \mathcal {L}(a_1,\ldots ,a_k)$
satisfies
$a\in \mathcal {L}(a_1,\ldots ,a_k)$
satisfies
(Equivalently, we could require that
![]() $p(t)\in \mathbb {Z}[t]$
, because this is a condition on all the linear combinations of the functions
$p(t)\in \mathbb {Z}[t]$
, because this is a condition on all the linear combinations of the functions
![]() $a_1,\ldots ,a_k$
.) Then, we have the following.
$a_1,\ldots ,a_k$
.) Then, we have the following.
-
(i) For any collection of nilmanifolds
 $X_i=G_i/\Gamma _i$
, elements
$X_i=G_i/\Gamma _i$
, elements
 $b_i\in G_i$
and
$b_i\in G_i$
and
 $x_i\in X_i$
, the sequence is equidistributed on the nilmanifold
$x_i\in X_i$
, the sequence is equidistributed on the nilmanifold $$ \begin{align*} ( b_1^{ \left\lfloor {a_1(n)} \right\rfloor }x_1,\ldots,b_k^{ \left\lfloor {a_k(n)} \right\rfloor }x_k ) \end{align*} $$
$$ \begin{align*} ( b_1^{ \left\lfloor {a_1(n)} \right\rfloor }x_1,\ldots,b_k^{ \left\lfloor {a_k(n)} \right\rfloor }x_k ) \end{align*} $$
 $\overline {(b_1^{\mathbb {N}} x_1)}\times \cdots \times \overline {(b_k^{\mathbb {N}} x_k)}$
.
$\overline {(b_1^{\mathbb {N}} x_1)}\times \cdots \times \overline {(b_k^{\mathbb {N}} x_k)}$
.
-
(ii) For any collection of nilmanifolds
 $X_i=G_i/\Gamma _i$
such that the groups
$X_i=G_i/\Gamma _i$
such that the groups
 $G_i$
are connected, simply connected, elements
$G_i$
are connected, simply connected, elements
 $b_i\in G_i$
and
$b_i\in G_i$
and
 $x_i\in X_i$
, the sequence is equidistributed on the nilmanifold
$x_i\in X_i$
, the sequence is equidistributed on the nilmanifold $$ \begin{align*} ( b_1^{a_1(n)}x_1,\ldots,b_k^{a_k(n)}x_k ) \end{align*} $$
$$ \begin{align*} ( b_1^{a_1(n)}x_1,\ldots,b_k^{a_k(n)}x_k ) \end{align*} $$
 $\overline {(b_1^{\mathbb {R}} x_1)} \times \cdots \times \overline {(b_k^{\mathbb {R}} x_k)}$
.
$\overline {(b_1^{\mathbb {R}} x_1)} \times \cdots \times \overline {(b_k^{\mathbb {R}} x_k)}$
.
Remark 1.
-
(a) The connectedness assumptions imposed on part (ii) of the previous theorem ensure that all elements of the form
 $b^s$
where
$b^s$
where
 $b\in G$
and
$b\in G$
and
 $s\in \mathbb {R}$
are well defined (see also Appendix B for the definition of the element
$s\in \mathbb {R}$
are well defined (see also Appendix B for the definition of the element
 $b^s$
for non-integer s).
$b^s$
for non-integer s). -
(b) In regards to part (ii) of the previous theorem, we establish the more general statement that if
 $b_1,\ldots ,b_k$
commute, the sequence
$b_1,\ldots ,b_k$
commute, the sequence
 $b_1^{a_1(n)}\cdots b_k^{a_k(n)}\Gamma $
is equidistributed on the nilmanifold
$b_1^{a_1(n)}\cdots b_k^{a_k(n)}\Gamma $
is equidistributed on the nilmanifold
 $\overline {b_1^{\mathbb {R}}\cdots b_k^{\mathbb {R}}\Gamma }$
. The fact that this is indeed a more general statement can be seen by passing to the product nilmanifold
$\overline {b_1^{\mathbb {R}}\cdots b_k^{\mathbb {R}}\Gamma }$
. The fact that this is indeed a more general statement can be seen by passing to the product nilmanifold
 $X_1\times \cdots \times X_k$
. A similar assertion holds for Theorem 1.2 below and we provide more details on this deduction after Proposition 4.1.
$X_1\times \cdots \times X_k$
. A similar assertion holds for Theorem 1.2 below and we provide more details on this deduction after Proposition 4.1.
Observe that, in contrast to Theorem A, we have the term
![]() $t^{\varepsilon }$
in the denominator, which is just out of reach of the conjectured optimal term
$t^{\varepsilon }$
in the denominator, which is just out of reach of the conjectured optimal term
![]() $\log t$
. As an example, using Theorem 1.1, we can prove that for any elements
$\log t$
. As an example, using Theorem 1.1, we can prove that for any elements
![]() $b_1,b_2\in G$
, the sequence
$b_1,b_2\in G$
, the sequence
![]() $(b_1^{n\log n}\Gamma ,b_2^{n^{3/2}}\Gamma )$
is equidistributed on the nilmanifold
$(b_1^{n\log n}\Gamma ,b_2^{n^{3/2}}\Gamma )$
is equidistributed on the nilmanifold
![]() $(\overline {b_1^{\mathbb {R}}\Gamma },\overline {b_2^{\mathbb {R}}\Gamma })$
, assuming that G satisfies the appropriate connectedness assumptions since we want these elements to be well defined.
$(\overline {b_1^{\mathbb {R}}\Gamma },\overline {b_2^{\mathbb {R}}\Gamma })$
, assuming that G satisfies the appropriate connectedness assumptions since we want these elements to be well defined.
If we have functions that are not linearly independent, then the above theorem fails, as can be seen by noting that the sequence
![]() $(n^{3/2},n^{1/2},n^{3/2}+n^{1/2})$
is not equidistributed on
$(n^{3/2},n^{1/2},n^{3/2}+n^{1/2})$
is not equidistributed on
![]() $\mathbb {T}^{3}$
. However, we can relax the linear independence condition in Theorem 1.1 and still obtain a convergence result.
$\mathbb {T}^{3}$
. However, we can relax the linear independence condition in Theorem 1.1 and still obtain a convergence result.
Theorem 1.2. Let
![]() $\mathcal {H}$
be a Hardy field containing the polynomial functions. Let
$\mathcal {H}$
be a Hardy field containing the polynomial functions. Let
![]() $a_1,\ldots ,a_k$
be functions in
$a_1,\ldots ,a_k$
be functions in
![]() $\mathcal {H}$
that have polynomial growth. Assume that there exists
$\mathcal {H}$
that have polynomial growth. Assume that there exists
![]() $\varepsilon>0$
, such that every function
$\varepsilon>0$
, such that every function
![]() $a\in \mathcal {L}(a_1,\ldots ,a_k)$
satisfies either
$a\in \mathcal {L}(a_1,\ldots ,a_k)$
satisfies either
or
Then, we have the following.
-
(i) For any collection of nilmanifolds
 $X_i=G_i/\Gamma _i$
, elements
$X_i=G_i/\Gamma _i$
, elements
 $b_i\in G_i$
,
$b_i\in G_i$
,
 $x_i\in X_i$
and continuous functions
$x_i\in X_i$
and continuous functions
 $f_1,\ldots ,f_k$
with complex values, the averages converge.
$f_1,\ldots ,f_k$
with complex values, the averages converge. $$ \begin{align*} \frac{1}{N}\sum_{i=1}^{N} f_1(b_1^{ \left\lfloor {a_1(n)} \right\rfloor }x_1)\cdots f_k(b_k^{ \left\lfloor {a_k(n)} \right\rfloor }x_k) \end{align*} $$
$$ \begin{align*} \frac{1}{N}\sum_{i=1}^{N} f_1(b_1^{ \left\lfloor {a_1(n)} \right\rfloor }x_1)\cdots f_k(b_k^{ \left\lfloor {a_k(n)} \right\rfloor }x_k) \end{align*} $$
-
(ii) For any collection of nilmanifolds
 $X_i=G_i/\Gamma _i$
such that the groups
$X_i=G_i/\Gamma _i$
such that the groups
 $G_i$
are connected, simply connected, elements
$G_i$
are connected, simply connected, elements
 $b_i\in G_i$
,
$b_i\in G_i$
,
 $x_i\in X_i$
and continuous functions
$x_i\in X_i$
and continuous functions
 $f_1,\ldots ,f_k$
with complex values, the averages converge.
$f_1,\ldots ,f_k$
with complex values, the averages converge. $$ \begin{align*} \frac{1}{N}\sum_{i=1}^{N} f_1(b_1^{a_1(n)}x_1) \cdots f_k(b_k^{a_k(n)}x_k) \end{align*} $$
$$ \begin{align*} \frac{1}{N}\sum_{i=1}^{N} f_1(b_1^{a_1(n)}x_1) \cdots f_k(b_k^{a_k(n)}x_k) \end{align*} $$
The main distinction between Theorems 1.1 and 1.2 is that in the second case, we allow for linear dependencies between the functions
![]() $a_1(t),\ldots , a_k(t)$
(for example, we may have the functions
$a_1(t),\ldots , a_k(t)$
(for example, we may have the functions
![]() $(t\log t, t^{3/2},t^{3/2}+t\log t)$
). We will use this theorem to deduce a convergence result for multiple ergodic averages (Theorem 1.3 below).
$(t\log t, t^{3/2},t^{3/2}+t\log t)$
). We will use this theorem to deduce a convergence result for multiple ergodic averages (Theorem 1.3 below).
Theorems 1.1 and 1.2 extend the equidistribution result of Theorem C from [Reference Frantzikinakis4], where the functions
![]() $a_1,\ldots ,a_k$
were assumed to have different growth rates and satisfy the growth condition in equation (4). However, our results are complementary to the results in [Reference Richter17], in the sense that both Theorem 1.1 and Theorem D each cover collections of functions that are not implied by the other one. The main difference between our results and the results in the previous literature (in the case of general k) is that prior results did not cover functions in the range
$a_1,\ldots ,a_k$
were assumed to have different growth rates and satisfy the growth condition in equation (4). However, our results are complementary to the results in [Reference Richter17], in the sense that both Theorem 1.1 and Theorem D each cover collections of functions that are not implied by the other one. The main difference between our results and the results in the previous literature (in the case of general k) is that prior results did not cover functions in the range
![]() $t^{\ell }\prec a(t)\ll t^{\ell }\log t$
, where
$t^{\ell }\prec a(t)\ll t^{\ell }\log t$
, where
![]() $\ell $
is a positive integer. Our method circumvents this restriction and can handle all families of functions of the form
$\ell $
is a positive integer. Our method circumvents this restriction and can handle all families of functions of the form
![]() $\sum _{i=1}^{k} c_it^{a_i}(\log t)^{b_i}$
, where
$\sum _{i=1}^{k} c_it^{a_i}(\log t)^{b_i}$
, where
![]() $a_i>0$
and
$a_i>0$
and
![]() $b_i,c_i\in \mathbb {R}$
(assuming, of course, that the linear combinations of the involved functions satisfy either equation (8) or equation (9)). However, our method has a drawback. As we stated, there are cases covered in the results of [Reference Richter17] that do not follow from the arguments present in this paper. These examples concern functions that grow slower than fractional powers
$b_i,c_i\in \mathbb {R}$
(assuming, of course, that the linear combinations of the involved functions satisfy either equation (8) or equation (9)). However, our method has a drawback. As we stated, there are cases covered in the results of [Reference Richter17] that do not follow from the arguments present in this paper. These examples concern functions that grow slower than fractional powers
![]() $t^{\delta }$
, such as the function
$t^{\delta }$
, such as the function
![]() $\log ^c t$
for
$\log ^c t$
for
![]() $c>0$
or the function
$c>0$
or the function
![]() $\exp (\sqrt {\log t})$
. An example that is not covered by Theorem 1.2 is the pair of functions
$\exp (\sqrt {\log t})$
. An example that is not covered by Theorem 1.2 is the pair of functions
![]() $(\log ^2 t, t^{3/2})$
. However, this last pair of functions can be covered by the results in [Reference Richter17]. We shall discuss the techniques and limitations of our proof in depth below (§1.3).
$(\log ^2 t, t^{3/2})$
. However, this last pair of functions can be covered by the results in [Reference Richter17]. We shall discuss the techniques and limitations of our proof in depth below (§1.3).
Combining Theorem 1.2 and the results in [Reference Tsinas18] on characteristic factors, we get a mean convergence result for multiple ergodic averages. Since the seminorm estimates for such averages were established in [Reference Tsinas18] under particular assumptions on our Hardy field
![]() $\mathcal {H}$
, these have to be incorporated into our statement. We will not need to use these assumptions anywhere else in this article, however.
$\mathcal {H}$
, these have to be incorporated into our statement. We will not need to use these assumptions anywhere else in this article, however.
Theorem 1.3. Let
![]() $\mathcal {H}$
be a Hardy field that contains the field
$\mathcal {H}$
be a Hardy field that contains the field
![]() $\mathcal {LE}$
of logarithmico- exponential functions and is closed under composition and compositional inversion of functions (when defined). Furthermore, assume that the functions
$\mathcal {LE}$
of logarithmico- exponential functions and is closed under composition and compositional inversion of functions (when defined). Furthermore, assume that the functions
![]() $a_1,\ldots ,a_k\in \mathcal {H}$
are as in Theorem 1.2. Then, for any measure-preserving system
$a_1,\ldots ,a_k\in \mathcal {H}$
are as in Theorem 1.2. Then, for any measure-preserving system
![]() $(X,\mu ,T)$
and any functions
$(X,\mu ,T)$
and any functions
![]() $f_1,\ldots ,f_k\in L^{\infty }(\mu )$
, the averages
$f_1,\ldots ,f_k\in L^{\infty }(\mu )$
, the averages
 $$ \begin{align} \frac{1}{N}\sum_{n=1}^{N} T^{ \left\lfloor {a_1(n)} \right\rfloor }f_1 \cdots T^{ \left\lfloor {a_k(n)} \right\rfloor }f_k \end{align} $$
$$ \begin{align} \frac{1}{N}\sum_{n=1}^{N} T^{ \left\lfloor {a_1(n)} \right\rfloor }f_1 \cdots T^{ \left\lfloor {a_k(n)} \right\rfloor }f_k \end{align} $$
converge in
![]() $L^2(\mu )$
.
$L^2(\mu )$
.
An example of a Hardy field that satisfies the above property is the Hardy field of Pfaffian functions (for the definition, see, for instance, [Reference Tsinas18, §2]).
It follows from the results in [Reference Tsinas18] that if the functions
![]() $a_1,\ldots ,a_k$
are as in Theorem 1.1 (actually, the
$a_1,\ldots ,a_k$
are as in Theorem 1.1 (actually, the
![]() $t^{\varepsilon }$
term can be replaced with the optimal term
$t^{\varepsilon }$
term can be replaced with the optimal term
![]() $\log t$
), then for any ergodic measure-preserving system
$\log t$
), then for any ergodic measure-preserving system
![]() $(X,\mu ,T)$
and bounded functions
$(X,\mu ,T)$
and bounded functions
![]() $f_1,\ldots ,f_k$
, the averages
$f_1,\ldots ,f_k$
, the averages
 $$ \begin{align*} \frac{1}{N}\sum_{i=1}^{N} f_1(T^{ \left\lfloor {a_1(n)} \right\rfloor }x)\cdots f_k(T^{ \left\lfloor {a_k(n)} \right\rfloor }x) \end{align*} $$
$$ \begin{align*} \frac{1}{N}\sum_{i=1}^{N} f_1(T^{ \left\lfloor {a_1(n)} \right\rfloor }x)\cdots f_k(T^{ \left\lfloor {a_k(n)} \right\rfloor }x) \end{align*} $$
converge in the
![]() $L^2$
-sense to the product of the integrals
$L^2$
-sense to the product of the integrals
![]() $\int f_1\,d\mu \cdot \cdots \cdot \int f_k\,d\mu $
. The methods used in that article cannot work when there are linear dependencies between the functions
$\int f_1\,d\mu \cdot \cdots \cdot \int f_k\,d\mu $
. The methods used in that article cannot work when there are linear dependencies between the functions
![]() $a_1,\ldots ,a_k$
(since they rely on the joint ergodicity results from [Reference Frantzikinakis6]). Therefore, to prove Theorem 1.3, we have to show that the Host–Kra factors are characteristic for these averages, reduce the problem to nilmanifolds using the Host–Kra structure theorem (see Theorem E in §2) and then tackle the problem of mean convergence in nilmanifolds. The first part of the above argument follows from the results in [Reference Tsinas18] (see Proposition 4.3), while Theorem 1.2 gives the stronger result of pointwise convergence when the system
$a_1,\ldots ,a_k$
(since they rely on the joint ergodicity results from [Reference Frantzikinakis6]). Therefore, to prove Theorem 1.3, we have to show that the Host–Kra factors are characteristic for these averages, reduce the problem to nilmanifolds using the Host–Kra structure theorem (see Theorem E in §2) and then tackle the problem of mean convergence in nilmanifolds. The first part of the above argument follows from the results in [Reference Tsinas18] (see Proposition 4.3), while Theorem 1.2 gives the stronger result of pointwise convergence when the system
![]() $(X,\mu , T)$
is a nilsystem. We comment here that the optimal restrictions on the functions
$(X,\mu , T)$
is a nilsystem. We comment here that the optimal restrictions on the functions
![]() $a_1,\ldots ,a_k$
in Theorem 1.3 are expected to be that the functions are good for convergence when the system
$a_1,\ldots ,a_k$
in Theorem 1.3 are expected to be that the functions are good for convergence when the system
![]() $(X,\mu , T)$
is a rotation on some torus
$(X,\mu , T)$
is a rotation on some torus
![]() $\mathbb {T}^d$
. A refuted conjecture of Frantzikinakis appears in [Reference Frantzikinakis5, Problem 22], although the statement needs to be changed to the following (personal communication).
$\mathbb {T}^d$
. A refuted conjecture of Frantzikinakis appears in [Reference Frantzikinakis5, Problem 22], although the statement needs to be changed to the following (personal communication).
Conjecture 2. Let
![]() $a_1,\ldots ,a_k$
be functions in
$a_1,\ldots ,a_k$
be functions in
![]() $\mathcal {LE}$
(or any other Hardy field) such that for all real numbers
$\mathcal {LE}$
(or any other Hardy field) such that for all real numbers
![]() $t_1,\ldots ,t_k\in [0,1)$
, the averages
$t_1,\ldots ,t_k\in [0,1)$
, the averages
 $$ \begin{align} \frac{1}{N}\sum_{n=1}^{N} e(t_1 \left\lfloor {a_1(n)} \right\rfloor +\cdots +t_k \left\lfloor {a_k(n)} \right\rfloor ) \end{align} $$
$$ \begin{align} \frac{1}{N}\sum_{n=1}^{N} e(t_1 \left\lfloor {a_1(n)} \right\rfloor +\cdots +t_k \left\lfloor {a_k(n)} \right\rfloor ) \end{align} $$
converge. Then, for any measure-preserving system
![]() $(X,\mu ,T)$
and functions
$(X,\mu ,T)$
and functions
![]() $f_1,\ldots ,f_k\in L^{\infty }(\mu )$
, the averages
$f_1,\ldots ,f_k\in L^{\infty }(\mu )$
, the averages
 $$ \begin{align} \frac{1}{N}\sum_{n=1}^{N} T^{ \left\lfloor {a_1(n)} \right\rfloor }f_1 \cdots T^{ \left\lfloor {a_k(n)} \right\rfloor }f_k \end{align} $$
$$ \begin{align} \frac{1}{N}\sum_{n=1}^{N} T^{ \left\lfloor {a_1(n)} \right\rfloor }f_1 \cdots T^{ \left\lfloor {a_k(n)} \right\rfloor }f_k \end{align} $$
converge in
![]() $L^2(\mu )$
and, if
$L^2(\mu )$
and, if
![]() $(X,\mu ,T)$
is a nilsystem and the functions
$(X,\mu ,T)$
is a nilsystem and the functions
![]() $f_1,\ldots ,f_k$
are continuous, then those averages converge pointwise everywhere.
$f_1,\ldots ,f_k$
are continuous, then those averages converge pointwise everywhere.
Remark 2. It can be shown that the above condition on the exponentials of the involved sequences is not sufficient if we replace the Hardy sequences with other, more general, sequences. Indeed, [Reference Frantzikinakis, Lesigne and Wierdl7, Theorem B] provides an example of a sequence
![]() $a(n)$
, such that for
$a(n)$
, such that for
![]() $a_1(n)=a(n)$
and
$a_1(n)=a(n)$
and
![]() $a_2(n)=2a(n)$
, the averages
$a_2(n)=2a(n)$
, the averages
 $$ \begin{align*} \frac{1}{N}\sum_{n=1}^{N} e(t_1a_1(n)+t_2a_2(n)) \end{align*} $$
$$ \begin{align*} \frac{1}{N}\sum_{n=1}^{N} e(t_1a_1(n)+t_2a_2(n)) \end{align*} $$
converge for any
![]() $t_1,t_2\in [0,1)$
, but the ergodic averages
$t_1,t_2\in [0,1)$
, but the ergodic averages
 $$ \begin{align*} \frac{1}{N}\sum_{n=1}^{N} T^{a_1(n)}f_1\cdot T^{a_2(n)}f_2 \end{align*} $$
$$ \begin{align*} \frac{1}{N}\sum_{n=1}^{N} T^{a_1(n)}f_1\cdot T^{a_2(n)}f_2 \end{align*} $$
do not converge in mean.
1.3 Short overview of the proof and additional remarks
The main idea of the proof is that functions in
![]() $\mathcal {H}$
of polynomial growth can be approximated sufficiently well by polynomials in short intervals. The equidistribution properties of polynomial sequences in nilmanifolds, even on small intervals, are well understood from [Reference Green and Tao9]. We use these quantitative results of Green and Tao (see Theorem F in Appendix B) to show that the averages over small intervals are ‘close’ to the integral of a continuous function in our nilmanifold. This approach was used in [Reference Frantzikinakis4] to show that (following the notation of Theorem 1.1) the sequence
$\mathcal {H}$
of polynomial growth can be approximated sufficiently well by polynomials in short intervals. The equidistribution properties of polynomial sequences in nilmanifolds, even on small intervals, are well understood from [Reference Green and Tao9]. We use these quantitative results of Green and Tao (see Theorem F in Appendix B) to show that the averages over small intervals are ‘close’ to the integral of a continuous function in our nilmanifold. This approach was used in [Reference Frantzikinakis4] to show that (following the notation of Theorem 1.1) the sequence
![]() $b^{a(n)}$
is equidistributed for all
$b^{a(n)}$
is equidistributed for all
![]() $b\in G$
and any function
$b\in G$
and any function
![]() $a(n)$
satisfying equation (P). In the case that we need to cover here, there are more technical difficulties in the proof, since we have to find polynomial expansions for several functions simultaneously, which also tend to be of increased complexity (for example, choosing the length of the short intervals is fairly straightforward in the case of one function, but not when someone deals with several functions in
$a(n)$
satisfying equation (P). In the case that we need to cover here, there are more technical difficulties in the proof, since we have to find polynomial expansions for several functions simultaneously, which also tend to be of increased complexity (for example, choosing the length of the short intervals is fairly straightforward in the case of one function, but not when someone deals with several functions in
![]() $\mathcal {H}$
). This idea of using a common polynomial expansion was also used recently by the author to establish the corresponding problem of finding characteristic factors for ergodic averages involving Hardy field iterates. This approach is well suited to handle functions in the range
$\mathcal {H}$
). This idea of using a common polynomial expansion was also used recently by the author to establish the corresponding problem of finding characteristic factors for ergodic averages involving Hardy field iterates. This approach is well suited to handle functions in the range
![]() $t^k\prec a(t)\prec t^k\log t$
, which were previously not known in the literature. Some additional care needs to be taken to separate polynomial functions and functions that we call ‘strongly non-polynomial’ (see Definition 2.1). This is an elementary argument and is carried out in Lemma A.5 in Appendix A. A similar ‘decomposition’ idea is present in [Reference Richter17, Lemma A.3] (also used in [Reference Tsinas18]), but we cannot use the exact same decomposition here, because some information on the linear combinations of our functions would be lost.
$t^k\prec a(t)\prec t^k\log t$
, which were previously not known in the literature. Some additional care needs to be taken to separate polynomial functions and functions that we call ‘strongly non-polynomial’ (see Definition 2.1). This is an elementary argument and is carried out in Lemma A.5 in Appendix A. A similar ‘decomposition’ idea is present in [Reference Richter17, Lemma A.3] (also used in [Reference Tsinas18]), but we cannot use the exact same decomposition here, because some information on the linear combinations of our functions would be lost.
Our argument differs quite a bit from the methods used in [Reference Richter17], which relied on applications of the van der Corput inequality as a means of complexity reduction and qualitative equidistribution results on nilmanifolds. In simplistic terms, this replaces the issue of studying equidistribution for a function
![]() $a(t)\in \mathcal {H}$
by the problem of studying equidistribution properties for the derivatives
$a(t)\in \mathcal {H}$
by the problem of studying equidistribution properties for the derivatives
![]() $a', a", a"'$
and so on. This cannot be used to cover, for example, functions in the range
$a', a", a"'$
and so on. This cannot be used to cover, for example, functions in the range
![]() $t\prec a(t)\ll t\log t$
, because the derivative
$t\prec a(t)\ll t\log t$
, because the derivative
![]() $a'$
must satisfy
$a'$
must satisfy
![]() $a'(t)\ll \log t$
, which does not have good equidistribution properties even on the 1-dimensional torus
$a'(t)\ll \log t$
, which does not have good equidistribution properties even on the 1-dimensional torus
![]() $\mathbb {T}$
. As we mentioned above, we can sidestep this situation, but our argument also has limitations. More precisely, we do not cover functions that grow very slowly (which we call sub-fractional functions). A sample of a ‘slow-growing’ function that we cannot handle is the function
$\mathbb {T}$
. As we mentioned above, we can sidestep this situation, but our argument also has limitations. More precisely, we do not cover functions that grow very slowly (which we call sub-fractional functions). A sample of a ‘slow-growing’ function that we cannot handle is the function
![]() $\log ^c t$
for
$\log ^c t$
for
![]() $c>1$
(for instance, the pair
$c>1$
(for instance, the pair
![]() $(\log ^2t, t\log t)$
is not covered by Theorem 1.1). The main reason is that when we pass to averages on small intervals, these functions become approximately equal to a constant and our method of using the Taylor expansion breaks down. That explains the existence of the function
$(\log ^2t, t\log t)$
is not covered by Theorem 1.1). The main reason is that when we pass to averages on small intervals, these functions become approximately equal to a constant and our method of using the Taylor expansion breaks down. That explains the existence of the function
![]() $t^{\varepsilon }$
in equation (8) instead of the term
$t^{\varepsilon }$
in equation (8) instead of the term
![]() $\log t$
, which is speculated to be optimal.
$\log t$
, which is speculated to be optimal.
In addition, we do not cover the case where some of the functions
![]() $a_i(t)$
are real polynomials, because the reduction to a statement on connected simply connected Lie groups becomes a lot more complicated. For example, consider a nilmanifold
$a_i(t)$
are real polynomials, because the reduction to a statement on connected simply connected Lie groups becomes a lot more complicated. For example, consider a nilmanifold
![]() $X=G/\Gamma $
with G connected and simply connected and elements
$X=G/\Gamma $
with G connected and simply connected and elements
![]() $b_1,b_2\in G$
that commute. It is not clear how to describe sufficiently well the orbit of the sequence
$b_1,b_2\in G$
that commute. It is not clear how to describe sufficiently well the orbit of the sequence
![]() $b_1^{n^{3/2}}b_2^{n^2}\Gamma $
on X. Alternatively, invoking Leibman’s theorem on polynomial orbits (Theorem B), we can describe the orbit
$b_1^{n^{3/2}}b_2^{n^2}\Gamma $
on X. Alternatively, invoking Leibman’s theorem on polynomial orbits (Theorem B), we can describe the orbit
![]() $\overline {\{b^{n^2}\Gamma \}}$
, while the nilmanifold
$\overline {\{b^{n^2}\Gamma \}}$
, while the nilmanifold
![]() $\overline {b_1^{\mathbb {R}}\Gamma }$
(which can be shown to be equal to the closure of the orbit
$\overline {b_1^{\mathbb {R}}\Gamma }$
(which can be shown to be equal to the closure of the orbit
![]() $b^{n^{3/2}}\Gamma $
by Theorem C) can be expressed in a nice form by Ratner’s theorem (see also Lemma B.1). However, we do not know how to accomplish this for their product
$b^{n^{3/2}}\Gamma $
by Theorem C) can be expressed in a nice form by Ratner’s theorem (see also Lemma B.1). However, we do not know how to accomplish this for their product
![]() $b_1^{n^{3/2}}b_2^{n^2}\Gamma $
. For example, we expect that this sequence equidistributes on some subnilmanifold Y (possibly after restricting to an arithmetic progression), but we cannot get any information on the underlying Lie group that defines Y, which is necessary when applying Theorem F.
$b_1^{n^{3/2}}b_2^{n^2}\Gamma $
. For example, we expect that this sequence equidistributes on some subnilmanifold Y (possibly after restricting to an arithmetic progression), but we cannot get any information on the underlying Lie group that defines Y, which is necessary when applying Theorem F.
A simple argument reduces our problem to the case when the Lie group G is connected and simply connected. Namely, we will prove Theorem 1.2 under the above connectedness assumptions. We sketch this reduction in Appendix B (at the end of §B.1). Therefore, we make the following convention:
1.4 Notational conventions
Throughout this article, we denote by
![]() $\mathbb {N}=\{1,2,\ldots \}$
the set of natural numbers. We denote
$\mathbb {N}=\{1,2,\ldots \}$
the set of natural numbers. We denote
![]() $\mathbb {T}^d=\mathbb {R}^d/\mathbb {Z}^{d}$
,
$\mathbb {T}^d=\mathbb {R}^d/\mathbb {Z}^{d}$
,
![]() $e(t)=e^{2\pi it}$
, while
$e(t)=e^{2\pi it}$
, while
![]() $\lVert x \rVert _{\mathbb {T}}=d(x,\mathbb {Z})$
and
$\lVert x \rVert _{\mathbb {T}}=d(x,\mathbb {Z})$
and
![]() $\{x\}$
denote the distance of x from the nearest integer and the fractional part of x, respectively. For an element
$\{x\}$
denote the distance of x from the nearest integer and the fractional part of x, respectively. For an element
![]() ${\mathbf x}=(x_1,\ldots ,x_k)$
in
${\mathbf x}=(x_1,\ldots ,x_k)$
in
![]() $\mathbb {R}^k$
, we denote
$\mathbb {R}^k$
, we denote
![]() $|{\mathbf x}|= |x_1|+\cdots +|x_k|$
. Lastly, we denote by
$|{\mathbf x}|= |x_1|+\cdots +|x_k|$
. Lastly, we denote by
![]() $\mathbf {1}_A$
the characteristic function of a set A.
$\mathbf {1}_A$
the characteristic function of a set A.
For two sequences
![]() $a_n,b_n$
, we say that
$a_n,b_n$
, we say that
![]() $b_n$
dominates
$b_n$
dominates
![]() $a_n$
and write
$a_n$
and write
![]() $a_n\prec b_n$
or
$a_n\prec b_n$
or
![]() $a_n=o(b_n)$
, when
$a_n=o(b_n)$
, when
![]() $a_n/b_n$
goes to 0, as
$a_n/b_n$
goes to 0, as
![]() $n\to +\infty $
. In addition, we write
$n\to +\infty $
. In addition, we write
![]() $a_n\ll b_n$
or
$a_n\ll b_n$
or
![]() $a_n=O(b_n)$
, if there exists a positive constant C such that
$a_n=O(b_n)$
, if there exists a positive constant C such that
![]() $|a_n|\leq C|b_n|$
for large enough n. When we want to denote the dependence of this constant on some parameters
$|a_n|\leq C|b_n|$
for large enough n. When we want to denote the dependence of this constant on some parameters
![]() $h_1,\ldots ,h_k$
, we will use the notation
$h_1,\ldots ,h_k$
, we will use the notation
![]() $a_n=O_{h_1,\ldots ,h_k}(b_n)$
. We use identical notation for asymptotic relations between functions on some real variable t, where we understand that these hold when we take
$a_n=O_{h_1,\ldots ,h_k}(b_n)$
. We use identical notation for asymptotic relations between functions on some real variable t, where we understand that these hold when we take
![]() $t\to +\infty $
.
$t\to +\infty $
.
Finally, we use the symbol
![]() $\operatorname *{\mathrm {\mathbb {E}}}$
to denote averages (over a range that will be implicit by the corresponding subscripts each time). Throughout the rest of the article, we use the letters
$\operatorname *{\mathrm {\mathbb {E}}}$
to denote averages (over a range that will be implicit by the corresponding subscripts each time). Throughout the rest of the article, we use the letters
![]() $p,q$
to denote polynomials and
$p,q$
to denote polynomials and
![]() $\chi $
is used to denote a horizontal character. We will use
$\chi $
is used to denote a horizontal character. We will use
![]() $b_1,b_2,\ldots ,b_k$
or
$b_1,b_2,\ldots ,b_k$
or
![]() $u_1,u_2,\ldots ,u_k,w_1,\ldots ,w_k$
in the proofs to denote elements of a nilpotent Lie group G.
$u_1,u_2,\ldots ,u_k,w_1,\ldots ,w_k$
in the proofs to denote elements of a nilpotent Lie group G.
2 Background material
2.1 Measure-preserving systems and Host–Kra structure theorem
A measure-preserving system is a quadruple
![]() $(X,\mathcal {X},\mu ,T)$
, where
$(X,\mathcal {X},\mu ,T)$
, where
![]() $(X,\mathcal {X},\mu )$
is a Lebesgue probability space and T is an invertible measure-preserving map, that is,
$(X,\mathcal {X},\mu )$
is a Lebesgue probability space and T is an invertible measure-preserving map, that is,
![]() $\mu (T^{-1}(A))=\mu (A)$
for all
$\mu (T^{-1}(A))=\mu (A)$
for all
![]() $A\in \mathcal {X}$
. It is called ergodic if all the T-invariant functions are constant. For the purposes of this article, a factor of the system
$A\in \mathcal {X}$
. It is called ergodic if all the T-invariant functions are constant. For the purposes of this article, a factor of the system
![]() $(X,\mathcal {X},\mu , T)$
is a T-invariant sub-
$(X,\mathcal {X},\mu , T)$
is a T-invariant sub-
![]() $\sigma $
-algebra of
$\sigma $
-algebra of
![]() $\mathcal {X}$
. However, when there is no confusion, we will omit the
$\mathcal {X}$
. However, when there is no confusion, we will omit the
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {X}$
from the quadruple
$\mathcal {X}$
from the quadruple
![]() $(X,\mathcal {X},\mu , T)$
.
$(X,\mathcal {X},\mu , T)$
.
Let
![]() $(X,\mu ,T)$
be a measure-preserving system and let
$(X,\mu ,T)$
be a measure-preserving system and let
![]() $f\in L^{\infty }(\mu )$
. We define the Host–Kra uniformity seminorms inductively as follows:
$f\in L^{\infty }(\mu )$
. We define the Host–Kra uniformity seminorms inductively as follows:
and, for
![]() $s\in \mathbb {N}$
,
$s\in \mathbb {N}$
,
In the ergodic case, the existence of these limits and the fact that these quantities are indeed seminorms was established in [Reference Host and Kra11]. In the same article, it was shown that these seminorms give rise to a factor
![]() $\mathcal {Z}_{s-1}(X)$
of X for every
$\mathcal {Z}_{s-1}(X)$
of X for every
![]() $s\geq 1$
, which is characterized by the following relation:
$s\geq 1$
, which is characterized by the following relation:
The significance of these factors hinges on the following remarkable structure theorem of Host and Kra [Reference Host and Kra11].
Theorem E. (Host–Kra)
Let
![]() $(X,\mu ,T)$
be an ergodic system. Then, the factor
$(X,\mu ,T)$
be an ergodic system. Then, the factor
![]() $\mathcal {Z}_s(X)$
is an inverse limit of s-step nilsystems.
$\mathcal {Z}_s(X)$
is an inverse limit of s-step nilsystems.
The last property implies that there exist T-invariant sub-
![]() $\sigma $
-algebras
$\sigma $
-algebras
![]() $\mathcal {Z}_s(n), n\in \mathbb {N}$
that span
$\mathcal {Z}_s(n), n\in \mathbb {N}$
that span
![]() $\mathcal {Z}_s$
, such that the factor
$\mathcal {Z}_s$
, such that the factor
![]() $\mathcal {Z}_s(n)$
is isomorphic as a system to an s-step nilsystem.
$\mathcal {Z}_s(n)$
is isomorphic as a system to an s-step nilsystem.
2.2 Background on Hardy fields
Let
![]() $\mathcal {B}$
denote the set of germs at infinity of real-valued functions defined on a half-line
$\mathcal {B}$
denote the set of germs at infinity of real-valued functions defined on a half-line
![]() $[x,+\infty )$
. Then,
$[x,+\infty )$
. Then,
![]() $(\mathcal {B},+,\cdot )$
is a ring, and a sub-field
$(\mathcal {B},+,\cdot )$
is a ring, and a sub-field
![]() $\mathcal {H}$
of
$\mathcal {H}$
of
![]() $\mathcal {B}$
that is closed under differentiation is called a Hardy field. We will say that
$\mathcal {B}$
that is closed under differentiation is called a Hardy field. We will say that
![]() $a(n)$
is a Hardy sequence if for
$a(n)$
is a Hardy sequence if for
![]() $n\in \mathbb {N}$
large enough, we have
$n\in \mathbb {N}$
large enough, we have
![]() $a(n)=f(n)$
for a function
$a(n)=f(n)$
for a function
![]() $f\in \mathcal {H}$
.
$f\in \mathcal {H}$
.
Any two functions
![]() $f,g\in \mathcal {H}$
with g not identically zero are comparable, that is, the limit
$f,g\in \mathcal {H}$
with g not identically zero are comparable, that is, the limit
exists and thus it makes sense to compare their growth rates. In addition, every non-constant function in
![]() $\mathcal {H}$
is eventually monotone and, therefore, has a constant sign eventually. In Appendix A, we have collected some lemmas about growth rates of functions in
$\mathcal {H}$
is eventually monotone and, therefore, has a constant sign eventually. In Appendix A, we have collected some lemmas about growth rates of functions in
![]() $\mathcal {H}$
, which will be used frequently throughout the proofs. The proofs of these lemmas can be found in [Reference Tsinas18], so we shall omit most of them.
$\mathcal {H}$
, which will be used frequently throughout the proofs. The proofs of these lemmas can be found in [Reference Tsinas18], so we shall omit most of them.
We define below some notions that will be used repeatedly throughout the remainder of the paper.
Definition 2.1. Let a be a function in
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
-
(a) The function a has polynomial growth if there exists a positive integer k such that
 $f(t)\ll t^k$
. The smallest positive integer k for which this holds will be called the degree of a.
$f(t)\ll t^k$
. The smallest positive integer k for which this holds will be called the degree of a. -
(b) The function a is called sub-linear if
 $a(t)\prec t$
.
$a(t)\prec t$
. -
(c) The function a is called sub-fractional if
 $a(t)\prec t^{\varepsilon }$
for all
$a(t)\prec t^{\varepsilon }$
for all
 $\varepsilon>0$
.
$\varepsilon>0$
. -
(d) The function a is called strongly non-polynomial if, for any positive integer k, we have that the functions
 $a(t)$
and
$a(t)$
and
 $t^k$
have distinct growth rates.
$t^k$
have distinct growth rates.
If
![]() $a\in \mathcal {H}$
has polynomial growth, we will also say that the corresponding sequence
$a\in \mathcal {H}$
has polynomial growth, we will also say that the corresponding sequence
![]() $a(n)$
has polynomial growth throughout the article. To understand the definition, consider the functions
$a(n)$
has polynomial growth throughout the article. To understand the definition, consider the functions
![]() $a_1(t)= t^{2/3}$
,
$a_1(t)= t^{2/3}$
,
![]() $a_2(t)=\log ^2 t$
,
$a_2(t)=\log ^2 t$
,
![]() $a_3(t)= t+t^{1/2}$
and
$a_3(t)= t+t^{1/2}$
and
![]() $a_4(t)=\exp (t)$
. The first two functions are sub-linear, but the functions
$a_4(t)=\exp (t)$
. The first two functions are sub-linear, but the functions
![]() $a_3,a_4$
are not. The function
$a_3,a_4$
are not. The function
![]() $a_2(t)$
is the only sub-fractional function among the four functions (it grows slower than all fractional powers), while the strongly non-polynomial functions are
$a_2(t)$
is the only sub-fractional function among the four functions (it grows slower than all fractional powers), while the strongly non-polynomial functions are
![]() $a_1,a_2$
and
$a_1,a_2$
and
![]() $a_4$
(note that
$a_4$
(note that
![]() $a_3$
grows like the polynomial
$a_3$
grows like the polynomial
![]() $p(t)=t$
). The function
$p(t)=t$
). The function
![]() $a_4$
does not have polynomial growth.
$a_4$
does not have polynomial growth.
Remark 3. The definition of strongly non-polynomial presented here is slightly different than the one given in [Reference Tsinas18]. The definition in that article was that we have the growth relation
![]() $t^k \prec a(t)\prec t^{k+1}$
for
$t^k \prec a(t)\prec t^{k+1}$
for
![]() $k\in \mathbb {N}$
, which imposes polynomial growth on our function. In addition, our new definition also allows the inclusion of functions
$k\in \mathbb {N}$
, which imposes polynomial growth on our function. In addition, our new definition also allows the inclusion of functions
![]() $a(t)$
such that
$a(t)$
such that
![]() $\lim \nolimits _{t\to +\infty }|a(t)|=0$
, while the old one excludes these functions (we do this solely for technical reasons).
$\lim \nolimits _{t\to +\infty }|a(t)|=0$
, while the old one excludes these functions (we do this solely for technical reasons).
3 Preparations for the proof
In this section, we will collect some lemmas and make some reductions, which will be useful when we delve into the proof of Theorems 1.1 and 1.2 in the next section. In addition, we provide a specific example, which illustrates the central ideas of the proof of Theorem 1.2 and does not involve a lot of computations.
First of all, we present a lemma, which appears in [Reference Frantzikinakis4, Lemma 3.3]. We will use this lemma to reduce our problem of studying the long averages over an interval
![]() $[1, N]$
(like those appearing in Theorem 1.2) to averages in short intervals. Its proof is elementary and so we omit it.
$[1, N]$
(like those appearing in Theorem 1.2) to averages in short intervals. Its proof is elementary and so we omit it.
Lemma 3.1. Let
![]() $(a(n))_{n\in \mathbb {N}}$
be a bounded sequence of complex numbers. Assume that
$(a(n))_{n\in \mathbb {N}}$
be a bounded sequence of complex numbers. Assume that
for some positive function
![]() $L(t)$
with
$L(t)$
with
![]() $1\prec L(t)\prec t$
. Then, we also have
$1\prec L(t)\prec t$
. Then, we also have
3.1 An example of convergence
Assume
![]() $X=G/\Gamma $
is a nilmanifold with G connected and simply connected. We will show that the averages
$X=G/\Gamma $
is a nilmanifold with G connected and simply connected. We will show that the averages
converge for any
![]() $x\in X$
, where
$x\in X$
, where
![]() $b_1,b_2\in G$
.
$b_1,b_2\in G$
.
Using Lemma 3.1, it suffices to show that the averages
converge, for some sub-linear function
![]() $L(t)$
. Passing to the nilmanifold
$L(t)$
. Passing to the nilmanifold
![]() $X\times X$
, we see that our problem reduces to showing that the averages
$X\times X$
, we see that our problem reduces to showing that the averages
converge for any nilmanifold
![]() $X=G/\Gamma $
, commuting elements
$X=G/\Gamma $
, commuting elements
![]() $b_1,b_2\in G$
and function
$b_1,b_2\in G$
and function
![]() $F\in C(X)$
. (When we pass to the product
$F\in C(X)$
. (When we pass to the product
![]() $X\times X$
, we have to study the actions of the elements
$X\times X$
, we have to study the actions of the elements
![]() $(b_1,e_G)$
and
$(b_1,e_G)$
and
![]() $(e_G,b_2)$
, which clearly commute.) Due to density, we can actually pick
$(e_G,b_2)$
, which clearly commute.) Due to density, we can actually pick
![]() $F\in \text {Lip}(X)$
. We provide more details for this deduction in the next section (after Proposition 4.1).
$F\in \text {Lip}(X)$
. We provide more details for this deduction in the next section (after Proposition 4.1).
Let
![]() $X'$
denote the subnilmanifold
$X'$
denote the subnilmanifold
![]() $\overline {b_1^{\mathbb {R}} b_2^{\mathbb {R}}\Gamma }$
of X. By Lemma B.1, this set is indeed a subnilmanifold of X and has a representation as
$\overline {b_1^{\mathbb {R}} b_2^{\mathbb {R}}\Gamma }$
of X. By Lemma B.1, this set is indeed a subnilmanifold of X and has a representation as
![]() $H/\Delta $
, with H connected, simply connected and containing all elements
$H/\Delta $
, with H connected, simply connected and containing all elements
![]() $b_1^s$
and
$b_1^s$
and
![]() $b_2^s$
for any
$b_2^s$
for any
![]() $s\in \mathbb {R}$
. In this example, we will also assume that
$s\in \mathbb {R}$
. In this example, we will also assume that
![]() $X'=\overline {b_1^{\mathbb {Z}}b_2^{\mathbb {Z}}\Gamma }$
. In the main proof, we will use Lemma B.2 to reduce the general case of the theorem to this one.
$X'=\overline {b_1^{\mathbb {Z}}b_2^{\mathbb {Z}}\Gamma }$
. In the main proof, we will use Lemma B.2 to reduce the general case of the theorem to this one.
Using the Taylor expansion around the point N, we can write
 $$ \begin{align*} (N+h)^{3/2}=N^{3/2}+\frac{3}{2}hN^{1/2}+\frac{3h^2}{8N^{1/2}}-\frac{h^3}{16N^{3/2}}+\frac{3h^4}{128\xi_h^{5/2}} \quad \text{for some } \xi_h\in [N,N+h] \end{align*} $$
$$ \begin{align*} (N+h)^{3/2}=N^{3/2}+\frac{3}{2}hN^{1/2}+\frac{3h^2}{8N^{1/2}}-\frac{h^3}{16N^{3/2}}+\frac{3h^4}{128\xi_h^{5/2}} \quad \text{for some } \xi_h\in [N,N+h] \end{align*} $$
for every
![]() $0\leq h\leq L(N)$
. If we choose
$0\leq h\leq L(N)$
. If we choose
![]() $L(t)$
to satisfy
$L(t)$
to satisfy
then the last term in the above expansion is smaller than
![]() $o_N(1)$
, while the second to last term is unbounded. Similarly, we can write
$o_N(1)$
, while the second to last term is unbounded. Similarly, we can write
 $$ \begin{align*} (N+h)\log (N+h)&=N\log N +h(\log N+1)\\ &\quad+\frac{h^2}{2N}-\frac{h^3}{6\psi_h^2} \quad \text{for some } \psi_h\in [N,N+h]. \end{align*} $$
$$ \begin{align*} (N+h)\log (N+h)&=N\log N +h(\log N+1)\\ &\quad+\frac{h^2}{2N}-\frac{h^3}{6\psi_h^2} \quad \text{for some } \psi_h\in [N,N+h]. \end{align*} $$
If we choose again
![]() $L(t)$
to satisfy
$L(t)$
to satisfy
we can show that the last term is
![]() $o_N(1)$
, while the
$o_N(1)$
, while the
![]() $h^2$
term is unbounded. For instance, we can choose
$h^2$
term is unbounded. For instance, we can choose
![]() $L(t)=t^{3/5}$
and both growth conditions that we imposed will be satisfied.
$L(t)=t^{3/5}$
and both growth conditions that we imposed will be satisfied.
Since the function F is continuous, we can disregard the highest order terms in the above expansion since they are both
![]() $o_N(1)$
. Our problem reduces to showing that the averages
$o_N(1)$
. Our problem reduces to showing that the averages
converge. For the sake of simplicity, we will show that the averages
converge, since both of these statements follow from the same arguments. For convenience, we will also assume that
![]() $x=\Gamma $
.
$x=\Gamma $
.
Let
![]() $\delta>0$
. We consider the finite sequence
$\delta>0$
. We consider the finite sequence
and we show that if N is large enough, then it is
![]() $\delta $
-equidistributed on the subnilmanifold
$\delta $
-equidistributed on the subnilmanifold
![]() $X'=\overline {b_1^{\mathbb {R}}b_2^{\mathbb {R}}\Gamma }$
of X. It is apparent that
$X'=\overline {b_1^{\mathbb {R}}b_2^{\mathbb {R}}\Gamma }$
of X. It is apparent that
![]() $v(n)\Gamma $
is a polynomial sequence in
$v(n)\Gamma $
is a polynomial sequence in
![]() $X'$
. We consider the horizontal torus Z of
$X'$
. We consider the horizontal torus Z of
![]() $X'$
, which is isomorphic to some
$X'$
, which is isomorphic to some
![]() $\mathbb {T}^{d}$
(
$\mathbb {T}^{d}$
(
![]() $d\in \mathbb {N}$
) and we also let
$d\in \mathbb {N}$
) and we also let
![]() $\pi $
denote the projection map from
$\pi $
denote the projection map from
![]() $X'$
to
$X'$
to
![]() $ Z$
. If the given sequence is not
$ Z$
. If the given sequence is not
![]() $\delta $
-equidistributed (for a fixed value of N), we can invoke Theorem F to find a positive constant
$\delta $
-equidistributed (for a fixed value of N), we can invoke Theorem F to find a positive constant
![]() $M=M(X',\delta ) $
and a non-trivial horizontal character
$M=M(X',\delta ) $
and a non-trivial horizontal character
![]() $\chi _N$
of modulus at most M and such that
$\chi _N$
of modulus at most M and such that
Suppose
![]() $\chi _N$
descends to the character
$\chi _N$
descends to the character
on
![]() $\mathbb {T}^d$
, where
$\mathbb {T}^d$
, where
![]() $k_{1,N},\ldots ,k_{d,N}$
are integers. The fact that the modulus is bounded by M implies that
$k_{1,N},\ldots ,k_{d,N}$
are integers. The fact that the modulus is bounded by M implies that
Let us also write
![]() $\pi (b_1\Gamma )=(x_1,\ldots ,x_d)$
and
$\pi (b_1\Gamma )=(x_1,\ldots ,x_d)$
and
![]() $\pi (b_2\Gamma )=(y_1,\ldots ,y_d)$
. Then, the last inequality implies that
$\pi (b_2\Gamma )=(y_1,\ldots ,y_d)$
. Then, the last inequality implies that
 $$ \begin{align} \bigg\lVert e\bigg(\frac{h^3}{N^{3/2}}\sum_{i=1}^{d} k_{i,N}x_i +\frac{h^2}{N}\sum_{i=1}^{d} k_{i,N} y_i \bigg) \bigg\rVert_{C^{\infty}[L(N)]}\leq M. \end{align} $$
$$ \begin{align} \bigg\lVert e\bigg(\frac{h^3}{N^{3/2}}\sum_{i=1}^{d} k_{i,N}x_i +\frac{h^2}{N}\sum_{i=1}^{d} k_{i,N} y_i \bigg) \bigg\rVert_{C^{\infty}[L(N)]}\leq M. \end{align} $$
Assume there are infinitely many N for which this holds. Since there are only finitely many possible choices for the numbers
![]() $k_{1, N},\ldots ,k_{d, N}$
above, we conclude that there exists a character
$k_{1, N},\ldots ,k_{d, N}$
above, we conclude that there exists a character
![]() $\chi $
such that
$\chi $
such that
![]() $\lVert \chi (\pi (a(h))\Gamma ) \rVert _{C^{\infty }[L(N)]}\leq M$
holds for infinitely many
$\lVert \chi (\pi (a(h))\Gamma ) \rVert _{C^{\infty }[L(N)]}\leq M$
holds for infinitely many
![]() $N\in \mathbb {N}$
. Then, we rewrite equation (14) (
$N\in \mathbb {N}$
. Then, we rewrite equation (14) (
![]() $k_i$
are some integers independent of N) as
$k_i$
are some integers independent of N) as
 $$ \begin{align*} \bigg\lVert e\bigg(\frac{h^3}{N^{3/2}}\sum_{i=1}^{d} k_{i}x_i +\frac{h^2}{N}\sum_{i=1}^{d} k_{i} y_i \bigg) \bigg\rVert_{C^{\infty}[L(N)]}\leq M, \end{align*} $$
$$ \begin{align*} \bigg\lVert e\bigg(\frac{h^3}{N^{3/2}}\sum_{i=1}^{d} k_{i}x_i +\frac{h^2}{N}\sum_{i=1}^{d} k_{i} y_i \bigg) \bigg\rVert_{C^{\infty}[L(N)]}\leq M, \end{align*} $$
and this inequality holds for infinitely many N.
The definition of the
![]() $C^{\infty }[L(N)]$
norms implies that we have the relations
$C^{\infty }[L(N)]$
norms implies that we have the relations
 $$ \begin{align*} L(N)^3\bigg\lVert \frac{\sum_{i=1}^{d} k_ix_i }{N^{3/2}} \bigg\rVert_{\mathbb{T}}\leq M \end{align*} $$
$$ \begin{align*} L(N)^3\bigg\lVert \frac{\sum_{i=1}^{d} k_ix_i }{N^{3/2}} \bigg\rVert_{\mathbb{T}}\leq M \end{align*} $$
and
 $$ \begin{align*} L(N)^2\bigg\lVert \frac{\sum_{i=1}^{d} k_i y_i }{N} \bigg\rVert_{\mathbb{T}}\leq M \end{align*} $$
$$ \begin{align*} L(N)^2\bigg\lVert \frac{\sum_{i=1}^{d} k_i y_i }{N} \bigg\rVert_{\mathbb{T}}\leq M \end{align*} $$
for infinitely many N. Due to our choice of the function
![]() $L(N)$
, these relations fail for N sufficiently large unless
$L(N)$
, these relations fail for N sufficiently large unless
 $$ \begin{align*} \sum_{i=1}^{d} k_ix_i \in \mathbb{Z} \quad \text{and} \quad \sum_{i=1}^{d} k_i y_i \in \mathbb{Z}. \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{d} k_ix_i \in \mathbb{Z} \quad \text{and} \quad \sum_{i=1}^{d} k_i y_i \in \mathbb{Z}. \end{align*} $$
This implies that
![]() $\chi \circ \pi (b_1\Gamma )=\chi \circ \pi (b_2\Gamma )=0$
and, consequently, we must also have
$\chi \circ \pi (b_1\Gamma )=\chi \circ \pi (b_2\Gamma )=0$
and, consequently, we must also have
![]() $\chi \circ \pi (b_1^mb_2^n\Gamma )=0$
for any
$\chi \circ \pi (b_1^mb_2^n\Gamma )=0$
for any
![]() $m,n\in \mathbb {Z}$
. Since elements of this form are dense in
$m,n\in \mathbb {Z}$
. Since elements of this form are dense in
![]() $\overline {b_1^{\mathbb {R}}b_2^{\mathbb {R}}\Gamma }$
by our initial hypothesis, we get that
$\overline {b_1^{\mathbb {R}}b_2^{\mathbb {R}}\Gamma }$
by our initial hypothesis, we get that
![]() $\chi $
must be the trivial character, which is a contradiction.
$\chi $
must be the trivial character, which is a contradiction.
In conclusion, we have established that the sequence
![]() $(v(h)\Gamma )_{0\leq h\leq L(N)}$
is
$(v(h)\Gamma )_{0\leq h\leq L(N)}$
is
![]() $\delta $
-equidistributed for large enough N on
$\delta $
-equidistributed for large enough N on
![]() $X'=\overline {b_1^{\mathbb {R}}b_2^{\mathbb {R}}\Gamma }$
. The result now follows by sending
$X'=\overline {b_1^{\mathbb {R}}b_2^{\mathbb {R}}\Gamma }$
. The result now follows by sending
![]() $\delta \to 0$
. We also notice that the limit of the averages is
$\delta \to 0$
. We also notice that the limit of the averages is
![]() $\int _{X'} F \ d m_{X'}$
.
$\int _{X'} F \ d m_{X'}$
.
Remark 4. We describe briefly here why we have to use the
![]() $t^{\varepsilon }$
term in equation (8) instead of the conjectured optimal term
$t^{\varepsilon }$
term in equation (8) instead of the conjectured optimal term
![]() $\log t$
. Assuming we had the functions
$\log t$
. Assuming we had the functions
![]() $\log ^2 t$
and
$\log ^2 t$
and
![]() $t\log t$
in this example, then for any choice of the sub-linear function
$t\log t$
in this example, then for any choice of the sub-linear function
![]() $L(t)$
that would give a good polynomial approximation for the function
$L(t)$
that would give a good polynomial approximation for the function
![]() $t\log t$
, we would have
$t\log t$
, we would have
which suggests that the sequence
![]() $\log ^2 n$
is essentially constant in the small intervals
$\log ^2 n$
is essentially constant in the small intervals
![]() $[N, N+L(N)]$
. If we proceed exactly as in the above argument, the best we can actually show is that
$[N, N+L(N)]$
. If we proceed exactly as in the above argument, the best we can actually show is that
 $$ \begin{align*} \bigg| \underset{N\leq n\leq N+ L(N)}{\operatorname*{\mathrm{\mathbb{E}}}}F(b_1^{\log^2 n}b_2^{n\log n} \Gamma) -\int_{Y_2} F(b_1^{\log^2 N} y)\ dm_{Y_2}(y)\bigg|\leq \delta \lVert F(b_1^{\log^2 N }\cdot) \rVert_{\text{Lip}(Y_2)} \end{align*} $$
$$ \begin{align*} \bigg| \underset{N\leq n\leq N+ L(N)}{\operatorname*{\mathrm{\mathbb{E}}}}F(b_1^{\log^2 n}b_2^{n\log n} \Gamma) -\int_{Y_2} F(b_1^{\log^2 N} y)\ dm_{Y_2}(y)\bigg|\leq \delta \lVert F(b_1^{\log^2 N }\cdot) \rVert_{\text{Lip}(Y_2)} \end{align*} $$
for large enough N, where
![]() $Y_2=\overline {b_2^{\mathbb {R}}\Gamma }$
and
$Y_2=\overline {b_2^{\mathbb {R}}\Gamma }$
and
![]() $F(b_1^{\log ^2 N }\cdot )$
denotes the function
$F(b_1^{\log ^2 N }\cdot )$
denotes the function
![]() $y\to F(b_1^{\log ^2 N }y)$
defined on the nilmanifold
$y\to F(b_1^{\log ^2 N }y)$
defined on the nilmanifold
![]() $Y_2$
. However, the Lipschitz norm above is of the order
$Y_2$
. However, the Lipschitz norm above is of the order
![]() $\log ^2N \lVert F \rVert _{\text {Lip}(X)}$
, which diverges as
$\log ^2N \lVert F \rVert _{\text {Lip}(X)}$
, which diverges as
![]() $N\to +\infty $
, so this bound cannot be useful for any purposes.
$N\to +\infty $
, so this bound cannot be useful for any purposes.
Another approach would be to use the fact that the parameter M in Theorem F is of the form
![]() $\delta ^{-O(1)}$
, namely we have bounds that are polynomial in
$\delta ^{-O(1)}$
, namely we have bounds that are polynomial in
![]() $\delta $
. Thus, one could allow the parameter
$\delta $
. Thus, one could allow the parameter
![]() $\delta $
to vary with N. For instance, establishing a bound of the form
$\delta $
to vary with N. For instance, establishing a bound of the form
![]() $(\log N)^{-(2+\varepsilon )} \lVert F(b_1^{\log ^2 N }\cdot ) \rVert _{\text {Lip}(Y_2)}$
in place of the term
$(\log N)^{-(2+\varepsilon )} \lVert F(b_1^{\log ^2 N }\cdot ) \rVert _{\text {Lip}(Y_2)}$
in place of the term
![]() $\delta \lVert F(b_1^{\log ^2 N }\cdot ) \rVert _{\text {Lip}(Y_2)}$
(namely, showing that our sequence is
$\delta \lVert F(b_1^{\log ^2 N }\cdot ) \rVert _{\text {Lip}(Y_2)}$
(namely, showing that our sequence is
![]() $(\log N)^{-(2+\varepsilon )}$
-equidistributed) on the right-hand side of the above equation leads to a solution to the more general problem. (It would actually suffice to obtain this statement for almost all
$(\log N)^{-(2+\varepsilon )}$
-equidistributed) on the right-hand side of the above equation leads to a solution to the more general problem. (It would actually suffice to obtain this statement for almost all
![]() $N\in \mathbb {N}$
in the sense of natural density.) However, any bound of this type is incorrect in general. Indeed, assume that the horizontal torus of
$N\in \mathbb {N}$
in the sense of natural density.) However, any bound of this type is incorrect in general. Indeed, assume that the horizontal torus of
![]() $\overline {b_2^{\mathbb {R}}\Gamma }$
was
$\overline {b_2^{\mathbb {R}}\Gamma }$
was
![]() $\mathbb {T}^2$
and also let
$\mathbb {T}^2$
and also let
![]() $(b_{2,1},b_{2,2})\in \mathbb {T}^2$
denote the image of the element
$(b_{2,1},b_{2,2})\in \mathbb {T}^2$
denote the image of the element
![]() $b_2\Gamma $
under the projection map. Following the same approximations as the ones in the example, we would like to show that the finite polynomial sequence
$b_2\Gamma $
under the projection map. Following the same approximations as the ones in the example, we would like to show that the finite polynomial sequence
![]() $b_2^{h^2/N}\Gamma $
, where
$b_2^{h^2/N}\Gamma $
, where
![]() $0\leq h\leq L(N)$
, is
$0\leq h\leq L(N)$
, is
![]() $ (\log N)^{-(2+\varepsilon )}$
-equidistributed for almost all
$ (\log N)^{-(2+\varepsilon )}$
-equidistributed for almost all
![]() $N\in \mathbb {N}$
and for some suitable sub-linear function
$N\in \mathbb {N}$
and for some suitable sub-linear function
![]() $L(t)$
satisfying only
$L(t)$
satisfying only
![]() $L(t)\succ t^{1/2}$
. Then, an application of Theorem F implies that if this assertion does not hold, then there exists a positive constant C and a horizontal character
$L(t)\succ t^{1/2}$
. Then, an application of Theorem F implies that if this assertion does not hold, then there exists a positive constant C and a horizontal character
![]() $\chi $
of modulus at most
$\chi $
of modulus at most
![]() $\log ^C N$
, such that
$\log ^C N$
, such that
Equivalently, there exist integers
![]() $k_1,k_2$
with
$k_1,k_2$
with
![]() $|k_1|+|k_2|\leq \log ^C N$
such that
$|k_1|+|k_2|\leq \log ^C N$
such that
 $$ \begin{align*}L^{2}(N)\bigg\lVert \frac{k_1b_{2,1}+k_2b_{2,2}}{N} \bigg\rVert_{\mathbb{T}}\leq \log^C N.\end{align*} $$
$$ \begin{align*}L^{2}(N)\bigg\lVert \frac{k_1b_{2,1}+k_2b_{2,2}}{N} \bigg\rVert_{\mathbb{T}}\leq \log^C N.\end{align*} $$
Thus, we would get a contradiction if we showed that
 $$ \begin{align*}\min_{|k_1|,|k_2|\leq \log^C N} |k_1b_{2,1}+k_2b_{2,2}|\geq \frac{N\log^C N}{L^2(N)}\end{align*} $$
$$ \begin{align*}\min_{|k_1|,|k_2|\leq \log^C N} |k_1b_{2,1}+k_2b_{2,2}|\geq \frac{N\log^C N}{L^2(N)}\end{align*} $$
holds for N in a set of density 1. However, we note that bounds like the above depend on the diophantine properties of the numbers
![]() $b_{2,1},b_{2,2}$
. Indeed, let us suppose that
$b_{2,1},b_{2,2}$
. Indeed, let us suppose that
![]() ${\alpha = {b_{2,1}}/{ b_{2,2}}\leq 1}$
. If we divide by
${\alpha = {b_{2,1}}/{ b_{2,2}}\leq 1}$
. If we divide by
![]() $b_{2,2}$
, the last inequality can be rewritten as
$b_{2,2}$
, the last inequality can be rewritten as
 $$ \begin{align*}\min_{|k_1|,|k_2|\leq \log^C N }|k_1\alpha+k_2|\geq \frac{N\log^C N}{|b_{2,2}|L^2(N)}.\end{align*} $$
$$ \begin{align*}\min_{|k_1|,|k_2|\leq \log^C N }|k_1\alpha+k_2|\geq \frac{N\log^C N}{|b_{2,2}|L^2(N)}.\end{align*} $$
For a fixed choice of
![]() $k_1$
, the absolute value is minimized by picking
$k_1$
, the absolute value is minimized by picking
![]() $k_2$
to be the nearest integer to
$k_2$
to be the nearest integer to
![]() $-k_1\alpha .$
Thus, we would need to show that
$-k_1\alpha .$
Thus, we would need to show that
 $$ \begin{align*}\min_{ |k_1|\leq \log^C N }\lVert k_1\alpha \rVert_{\mathbb{T}}\geq \frac{N\log^C N}{|b_{2,2}|L^2(N)}\end{align*} $$
$$ \begin{align*}\min_{ |k_1|\leq \log^C N }\lVert k_1\alpha \rVert_{\mathbb{T}}\geq \frac{N\log^C N}{|b_{2,2}|L^2(N)}\end{align*} $$
and we can find
![]() $b_{2,1},b_{2,2}\in (0,1)$
for which this inequality fails for all N in a set of positive upper density. A simpler example that avoids the complicated function on the right-hand side of the last equation is to show that we can find
$b_{2,1},b_{2,2}\in (0,1)$
for which this inequality fails for all N in a set of positive upper density. A simpler example that avoids the complicated function on the right-hand side of the last equation is to show that we can find
![]() $\alpha \in (0,1)$
for which the inequality
$\alpha \in (0,1)$
for which the inequality
![]() $\min _{|k|\leq N}^{}\lVert k\alpha \rVert _{\mathbb {T}}\geq 2^{-n}$
fails for all
$\min _{|k|\leq N}^{}\lVert k\alpha \rVert _{\mathbb {T}}\geq 2^{-n}$
fails for all
![]() $N\in \mathbb {N}$
in a set of upper density 1. Indeed, we can construct an
$N\in \mathbb {N}$
in a set of upper density 1. Indeed, we can construct an
![]() $\alpha \in (0,1)$
such that
$\alpha \in (0,1)$
such that
![]() $\liminf \nolimits _{n\to +\infty }2^{2^n}\lVert n\alpha \rVert _{\mathbb {T}}=0$
. Thus, there is a sequence
$\liminf \nolimits _{n\to +\infty }2^{2^n}\lVert n\alpha \rVert _{\mathbb {T}}=0$
. Thus, there is a sequence
![]() $q_n$
such that
$q_n$
such that
![]() $\lVert q_na \rVert _{\mathbb {T}}\leq 2^{-2^{q_n}}$
which implies that
$\lVert q_na \rVert _{\mathbb {T}}\leq 2^{-2^{q_n}}$
which implies that
![]() $\min _{|k|\leq N}^{}\lVert k\alpha \rVert _{\mathbb {T}}\leq 2^{-2^{q_n}}\leq 2^{N}$
for every N with
$\min _{|k|\leq N}^{}\lVert k\alpha \rVert _{\mathbb {T}}\leq 2^{-2^{q_n}}\leq 2^{N}$
for every N with
![]() $q_n\leq N\leq 2^{q_n}$
. Thus, the set of N for which the above inequality fails has upper density 1.
$q_n\leq N\leq 2^{q_n}$
. Thus, the set of N for which the above inequality fails has upper density 1.
3.2 Removing the integer parts
In this part, we will establish a lemma that practically implies that part (a) of Theorem 1.2 follows from part (b) of the same theorem. The fact that part (a) of Theorem 1.1 follows from part (b) of the same theorem is precisely the statement of [Reference Frantzikinakis4, Lemma 5.1], which is proven using very similar arguments to the proof of Lemma 3.2 below. If a collection of sequences of real numbers has the property that the averages
converge for all nilmanifolds
![]() $X_i=G_i/\Gamma _i$
, elements
$X_i=G_i/\Gamma _i$
, elements
![]() $b_i\in G_i$
, points
$b_i\in G_i$
, points
![]() $x_i\in X_i$
and continuous functions
$x_i\in X_i$
and continuous functions
![]() $f_i$
defined on
$f_i$
defined on
![]() $X_i$
, we will say that this collection is pointwise good for nilsystems. The notation
$X_i$
, we will say that this collection is pointwise good for nilsystems. The notation
![]() $b_i^{a_i(n)}$
makes sense here due to the connectedness assumptions we have imposed on the Lie groups
$b_i^{a_i(n)}$
makes sense here due to the connectedness assumptions we have imposed on the Lie groups
![]() $G_i$
.
$G_i$
.
Lemma 3.2. Let
![]() $a_1(n),\ldots ,a_k(n)$
be sequences of real numbers that satisfy the following.
$a_1(n),\ldots ,a_k(n)$
be sequences of real numbers that satisfy the following.
-
(a) The collection
 $a_1(n),\ldots ,a_k(n)$
is pointwise good for nilsystems.
$a_1(n),\ldots ,a_k(n)$
is pointwise good for nilsystems. -
(b) For every
 $1\leq i\leq k$
, we have that the sequence
$1\leq i\leq k$
, we have that the sequence
 $(a_i(n)\mathbb {Z})_{n\in \mathbb {N}}$
satisfies one of the following:
$(a_i(n)\mathbb {Z})_{n\in \mathbb {N}}$
satisfies one of the following:
-
(1) it is equidistributed on
 $\mathbb {T}$
;
$\mathbb {T}$
; -
(2) it converges to some
 $c=c(i)\in \mathbb {T}$
different from
$c=c(i)\in \mathbb {T}$
different from
 $0$
;
$0$
; -
(3) it converges to 0 and the sequence
 $\{a_i(n)\}-\tfrac 12$
has a constant sign eventually.
$\{a_i(n)\}-\tfrac 12$
has a constant sign eventually.
Then, the sequences
![]() $ \left \lfloor {a_1(n)} \right \rfloor ,\ldots , \left \lfloor {a_k(n)} \right \rfloor $
are pointwise good for nilsystems.
$ \left \lfloor {a_1(n)} \right \rfloor ,\ldots , \left \lfloor {a_k(n)} \right \rfloor $
are pointwise good for nilsystems.
Remark 5. The number
![]() $\tfrac 12$
in the third condition is arbitrary since we could have used any number
$\tfrac 12$
in the third condition is arbitrary since we could have used any number
![]() $\alpha \in (0,1)$
. We primarily use this condition in the following manner: suppose we have a function
$\alpha \in (0,1)$
. We primarily use this condition in the following manner: suppose we have a function
![]() $f(t)$
, which converges monotonically to some
$f(t)$
, which converges monotonically to some
![]() $k\in \mathbb {Z}$
as
$k\in \mathbb {Z}$
as
![]() $t\to +\infty $
. Then, we clearly have
$t\to +\infty $
. Then, we clearly have
![]() $\lVert f(t) \rVert _{\mathbb {T}}\to 0$
and we also observe that the sequence
$\lVert f(t) \rVert _{\mathbb {T}}\to 0$
and we also observe that the sequence
![]() $\{f(n)\}$
does not not oscillate between intervals of the form
$\{f(n)\}$
does not not oscillate between intervals of the form
![]() $[0,\varepsilon ]$
and
$[0,\varepsilon ]$
and
![]() $[1-\varepsilon ,1)$
(due to the monotonicity assumption). Thus, the sequence
$[1-\varepsilon ,1)$
(due to the monotonicity assumption). Thus, the sequence
![]() $\{f(n)\}-\tfrac 12$
will indeed have a constant sign (positive if f increases to k and negative otherwise).
$\{f(n)\}-\tfrac 12$
will indeed have a constant sign (positive if f increases to k and negative otherwise).
Proof. Let
![]() $X_i=G_i/\Gamma _i$
be nilmanifolds with
$X_i=G_i/\Gamma _i$
be nilmanifolds with
![]() $G_i$
connected and simply connected and
$G_i$
connected and simply connected and
![]() $b_i\in G_i$
. Let
$b_i\in G_i$
. Let
![]() $f_1,\ldots ,f_k$
be continuous functions defined on
$f_1,\ldots ,f_k$
be continuous functions defined on
![]() $X_1,\ldots ,X_k$
, respectively. Under the hypotheses of the lemma on the sequences
$X_1,\ldots ,X_k$
, respectively. Under the hypotheses of the lemma on the sequences
![]() $a_1(n),\ldots ,a_k(n)$
, we want to show that the averages
$a_1(n),\ldots ,a_k(n)$
, we want to show that the averages
converge for any choice of the
![]() $x_i\in X_i$
.
$x_i\in X_i$
.
Fix some
![]() $i\in \{1,2,\ldots ,k\}$
. If the sequence
$i\in \{1,2,\ldots ,k\}$
. If the sequence
![]() $a_i(n)$
satisfies the second condition, namely that
$a_i(n)$
satisfies the second condition, namely that
![]() $a_i(n)\mathbb {Z}$
converges to
$a_i(n)\mathbb {Z}$
converges to
![]() $c\mathbb {Z}$
(
$c\mathbb {Z}$
(
![]() $c\neq 0$
), then for n sufficiently large, we have
$c\neq 0$
), then for n sufficiently large, we have
This implies that
![]() $b_i^{ \left \lfloor {a_i(n)} \right \rfloor }=b_i^{-\{c\}}b_i^{a_i(n)+o_n(1)}$
. Since the function
$b_i^{ \left \lfloor {a_i(n)} \right \rfloor }=b_i^{-\{c\}}b_i^{a_i(n)+o_n(1)}$
. Since the function
![]() $f_i$
is continuous, we can disregard the contribution of the
$f_i$
is continuous, we can disregard the contribution of the
![]() $o_n(1)$
term, while the
$o_n(1)$
term, while the
![]() $b_i^{-\{c\}}$
term can be absorbed by the
$b_i^{-\{c\}}$
term can be absorbed by the
![]() $x_i$
. Therefore, we notice that in this case, we can remove the integer part for the sequence
$x_i$
. Therefore, we notice that in this case, we can remove the integer part for the sequence
![]() $a_i(n)$
. An entirely similar argument demonstrates that the same holds if
$a_i(n)$
. An entirely similar argument demonstrates that the same holds if
![]() $a_i(n)$
satisfies the third condition.
$a_i(n)$
satisfies the third condition.
To complete the proof, we will consider below the case that each of the sequences
![]() $a_i(n)\mathbb {Z}$
is equidistributed on
$a_i(n)\mathbb {Z}$
is equidistributed on
![]() $\mathbb {T}$
for convenience (namely, they all satisfy the first condition). Since we can easily remove the integer parts for those sequences that satisfy the second or third condition as we did above, the argument below easily adapts to the general setting with some changes in notation.
$\mathbb {T}$
for convenience (namely, they all satisfy the first condition). Since we can easily remove the integer parts for those sequences that satisfy the second or third condition as we did above, the argument below easily adapts to the general setting with some changes in notation.
We rewrite the averages in equation (16) as
 $$ \begin{align*} \underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} \prod_{i=1}^k {f_i}(b_i^{-\{a_i(n)\}}b_i^{{a_i(n)}}x_i)= \underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} \prod_{i=1}^k \widetilde{f_i}(a_i(n)\mathbb{Z},b_i^{a_i(n)}x_i), \end{align*} $$
$$ \begin{align*} \underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} \prod_{i=1}^k {f_i}(b_i^{-\{a_i(n)\}}b_i^{{a_i(n)}}x_i)= \underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} \prod_{i=1}^k \widetilde{f_i}(a_i(n)\mathbb{Z},b_i^{a_i(n)}x_i), \end{align*} $$
where
![]() $\widetilde {f_i}:\mathbb {T}\times X_i\to \mathbb {C}$
is the function defined by the relation
$\widetilde {f_i}:\mathbb {T}\times X_i\to \mathbb {C}$
is the function defined by the relation
Let
![]() $v_i(n)$
be the sequence
$v_i(n)$
be the sequence
![]() $(a_i(n)\mathbb {Z},b_i^{a_i(n)}x_i)$
. By our hypothesis, for any continuous functions
$(a_i(n)\mathbb {Z},b_i^{a_i(n)}x_i)$
. By our hypothesis, for any continuous functions
![]() $f_i'$
on
$f_i'$
on
![]() $\widetilde {X_i}=\mathbb {T}\times X_i$
, the averages of
$\widetilde {X_i}=\mathbb {T}\times X_i$
, the averages of
![]() $\prod _{i=1}^{k}f_i'(v_i(n))$
converge. However, note that the functions
$\prod _{i=1}^{k}f_i'(v_i(n))$
converge. However, note that the functions
![]() $\widetilde {f_i}$
that we are dealing with may have discontinuities when s becomes close to an integer. Our goal is to approximate each
$\widetilde {f_i}$
that we are dealing with may have discontinuities when s becomes close to an integer. Our goal is to approximate each
![]() $\widetilde {f_i}$
by a continuous function and then use the above observation.
$\widetilde {f_i}$
by a continuous function and then use the above observation.
Let
![]() $\varepsilon>0$
. For every
$\varepsilon>0$
. For every
![]() $1\leq i\leq k$
, we define a continuous function
$1\leq i\leq k$
, we define a continuous function
![]() $f_{i,\varepsilon }$
that agrees everywhere with
$f_{i,\varepsilon }$
that agrees everywhere with
![]() $\widetilde {f_i}$
on
$\widetilde {f_i}$
on
![]() $[\varepsilon ,1-\varepsilon ]\times X_i$
and such that
$[\varepsilon ,1-\varepsilon ]\times X_i$
and such that
![]() $f_{i,\varepsilon }$
is bounded uniformly by
$f_{i,\varepsilon }$
is bounded uniformly by
![]() $2\lVert \widetilde {f_i} \rVert _{\infty }$
. Observe that
$2\lVert \widetilde {f_i} \rVert _{\infty }$
. Observe that
 $$ \begin{align} \bigg| \underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} \widetilde{f_i}(v_i(n))- \underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} {f_{i,\varepsilon}}(v_i(n)) \bigg| &=\frac{1}{N}\bigg|\sum_{\underset{ a_i(n)\notin [\varepsilon,1-\varepsilon]}{1\leq n\leq N} }^{}\bigg(\widetilde{f_i}(v_i(n))-{f_{i,\varepsilon}}(v_i(n))\bigg) \bigg| \nonumber\\ &\ll\varepsilon\lVert \widetilde{f_i} \rVert_{\infty}+o_N(1), \end{align} $$
$$ \begin{align} \bigg| \underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} \widetilde{f_i}(v_i(n))- \underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} {f_{i,\varepsilon}}(v_i(n)) \bigg| &=\frac{1}{N}\bigg|\sum_{\underset{ a_i(n)\notin [\varepsilon,1-\varepsilon]}{1\leq n\leq N} }^{}\bigg(\widetilde{f_i}(v_i(n))-{f_{i,\varepsilon}}(v_i(n))\bigg) \bigg| \nonumber\\ &\ll\varepsilon\lVert \widetilde{f_i} \rVert_{\infty}+o_N(1), \end{align} $$
where the last bound follows from the triangle inequality and the fact that
![]() $a_i(n)$
is equidistributed
$a_i(n)$
is equidistributed
![]() $(mod\ 1)$
, which indicates that the set
$(mod\ 1)$
, which indicates that the set
![]() $\{n\in \mathbb {N}\colon a_i(n)\notin [\varepsilon ,1-\varepsilon ]\}$
has asymptotic density
$\{n\in \mathbb {N}\colon a_i(n)\notin [\varepsilon ,1-\varepsilon ]\}$
has asymptotic density
![]() $2\varepsilon $
.
$2\varepsilon $
.
Combining equation (17) with a simple telescoping argument, we deduce that
 $$ \begin{align*} \limsup_{N\to+\infty} \bigg| \underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} \prod_{i=1}^k \widetilde{f_i}(v_i(n)) - \underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} \prod_{i=1}^{k}{f_{i,\varepsilon}}(v_i(n)) \bigg|\ll k\varepsilon\prod_{i=1}^k \lVert \widetilde{f_i} \rVert_{\infty}. \end{align*} $$
$$ \begin{align*} \limsup_{N\to+\infty} \bigg| \underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} \prod_{i=1}^k \widetilde{f_i}(v_i(n)) - \underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} \prod_{i=1}^{k}{f_{i,\varepsilon}}(v_i(n)) \bigg|\ll k\varepsilon\prod_{i=1}^k \lVert \widetilde{f_i} \rVert_{\infty}. \end{align*} $$
Since the averages
![]() $\underset {1\leq n\leq N}{\operatorname *{\mathrm {\mathbb {E}}}} \prod _{i=1}^k{f_{i,\varepsilon }}(v(n)) $
converge as
$\underset {1\leq n\leq N}{\operatorname *{\mathrm {\mathbb {E}}}} \prod _{i=1}^k{f_{i,\varepsilon }}(v(n)) $
converge as
![]() $N\to \infty $
by our hypothesis (the functions involved here are continuous), we infer that the averages
$N\to \infty $
by our hypothesis (the functions involved here are continuous), we infer that the averages
 $$ \begin{align*}\underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} \prod_{i=1}^k \widetilde{f_i}(v_i(n))\end{align*} $$
$$ \begin{align*}\underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} \prod_{i=1}^k \widetilde{f_i}(v_i(n))\end{align*} $$
form a Cauchy sequence and, therefore, converge. The conclusion follows.
Using the previous lemma, we can establish that the first part of Theorem 1.2 follows from the second part. We postpone this until the next section, where we also prove the second part of Theorem 1.2.
4 Proofs of main theorems
The main tool we are going to use in our proof is the quantitative Green–Tao theorem on polynomial orbits (Theorem F). A technical obstruction in our proof is that among the functions
![]() $a_1,\ldots ,a_k$
in the statement of Theorem 1.2, we must separate the polynomial functions from the strongly non-polynomial ones. We will accomplish this using an elementary lemma (Lemma A.5) which is proven in the Appendix. We restate Theorem 1.2 here.
$a_1,\ldots ,a_k$
in the statement of Theorem 1.2, we must separate the polynomial functions from the strongly non-polynomial ones. We will accomplish this using an elementary lemma (Lemma A.5) which is proven in the Appendix. We restate Theorem 1.2 here.
Theorem 1.2. Let
![]() $\mathcal {H}$
be a Hardy field that contains the polynomial functions. Let
$\mathcal {H}$
be a Hardy field that contains the polynomial functions. Let
![]() $a_1,\ldots ,a_k$
be functions in
$a_1,\ldots ,a_k$
be functions in
![]() $\mathcal {H}$
that have polynomial growth. Assume that there exists
$\mathcal {H}$
that have polynomial growth. Assume that there exists
![]() $\varepsilon>0$
, such that every function
$\varepsilon>0$
, such that every function
![]() $a\in \mathcal {L}(a_1,\ldots ,a_k)$
satisfies either
$a\in \mathcal {L}(a_1,\ldots ,a_k)$
satisfies either
or
Then, we have the following.
-
(i) For any collection of nilmanifolds
 $X_i=G_i/\Gamma _i$
, elements
$X_i=G_i/\Gamma _i$
, elements
 $b_i\in G_i$
,
$b_i\in G_i$
,
 $x_i\in X_i$
and continuous functions
$x_i\in X_i$
and continuous functions
 $f_1,\ldots ,f_k$
with complex values, the averages converge.
$f_1,\ldots ,f_k$
with complex values, the averages converge. $$ \begin{align*} \frac{1}{N}\sum_{i=1}^{N} f_1(b_1^{ \left\lfloor {a_1(n)} \right\rfloor }x_1) \cdots f_k(b_k^{ \left\lfloor {a_k(n)} \right\rfloor }x_k) \end{align*} $$
$$ \begin{align*} \frac{1}{N}\sum_{i=1}^{N} f_1(b_1^{ \left\lfloor {a_1(n)} \right\rfloor }x_1) \cdots f_k(b_k^{ \left\lfloor {a_k(n)} \right\rfloor }x_k) \end{align*} $$
-
(ii) For any collection of nilmanifolds
 $X_i=G_i/\Gamma _i$
such that the groups
$X_i=G_i/\Gamma _i$
such that the groups
 $G_i$
are connected, simply connected, elements
$G_i$
are connected, simply connected, elements
 $b_i,\in G_i$
,
$b_i,\in G_i$
,
 $x_i\in X_i$
and continuous functions
$x_i\in X_i$
and continuous functions
 $f_1,\ldots ,f_k$
with complex values, the averages converge.
$f_1,\ldots ,f_k$
with complex values, the averages converge. $$ \begin{align*} \frac{1}{N}\sum_{i=1}^{N} f_1(b_1^{a_1(n)}x_1)\cdots f_k(b_k^{a_k(n)}x_k) \end{align*} $$
$$ \begin{align*} \frac{1}{N}\sum_{i=1}^{N} f_1(b_1^{a_1(n)}x_1)\cdots f_k(b_k^{a_k(n)}x_k) \end{align*} $$
First of all, we show that the first part follows from the second part. This is accomplished by using Lemma 3.2. We remark again that in part (i), there are no connectedness assumptions made on the groups
![]() $G_i$
. Nonetheless, the convention equation (⋆) in §1 allows us to consider only the case that the Lie groups
$G_i$
. Nonetheless, the convention equation (⋆) in §1 allows us to consider only the case that the Lie groups
![]() $G_i$
are connected and simply connected. We implicitly work under this assumption in the proof below.
$G_i$
are connected and simply connected. We implicitly work under this assumption in the proof below.
Proof of part (i) of Theorem 1.2, assuming part (ii)
We will have to confirm that the conditions of Lemma 3.2 are satisfied. Let
![]() $a_1,\ldots ,a_k\in \mathcal {H}$
be as in the statement of Theorem 1.2. Condition (a) of Lemma 3.2 is satisfied by our hypothesis. Now, we verify the second condition.
$a_1,\ldots ,a_k\in \mathcal {H}$
be as in the statement of Theorem 1.2. Condition (a) of Lemma 3.2 is satisfied by our hypothesis. Now, we verify the second condition.
Fix some
![]() $i\in \{1,2,\ldots ,k\}$
. We consider three cases.
$i\in \{1,2,\ldots ,k\}$
. We consider three cases.
-
(i) Assume that the function
 $a_i(t)$
is such that
$a_i(t)$
is such that
 $|a_i(t)-q(t)|\succ t^{\varepsilon }$
for all polynomials
$|a_i(t)-q(t)|\succ t^{\varepsilon }$
for all polynomials
 $q(t)$
with rational coefficients. Then, the sequence
$q(t)$
with rational coefficients. Then, the sequence
 $a_i(n)\mathbb {Z}$
is equidistributed on
$a_i(n)\mathbb {Z}$
is equidistributed on
 $\mathbb {T}$
(satisfying condition (1)), due to Theorem A.
$\mathbb {T}$
(satisfying condition (1)), due to Theorem A. -
(ii) Assume that the function
 $a_i(t)$
is such that
$a_i(t)$
is such that
 $\lim \nolimits _{t\to +\infty } a_i(t)=c\notin \mathbb {Z}$
. Then, the sequence
$\lim \nolimits _{t\to +\infty } a_i(t)=c\notin \mathbb {Z}$
. Then, the sequence
 $a_i(n)$
satisfies condition (2) of Lemma 3.2.
$a_i(n)$
satisfies condition (2) of Lemma 3.2. -
(iii) Assume that neither of the above conditions is true. Since
 $a_i(t)$
must satisfy equation (9), we deduce that
$a_i(t)$
must satisfy equation (9), we deduce that
 $a_i(t)$
converges to some integer c. However, since
$a_i(t)$
converges to some integer c. However, since
 $a_i(t)$
converges to c monotonically (functions in
$a_i(t)$
converges to c monotonically (functions in
 $\mathcal {H}$
are eventually monotone), we deduce that condition (3) of Lemma 3.2 is satisfied and we are done.
$\mathcal {H}$
are eventually monotone), we deduce that condition (3) of Lemma 3.2 is satisfied and we are done.
Now we switch our attention to the proof of part (ii). First, we will apply Lemma A.5 from Appendix A to replace the original functions
![]() $a_1,\ldots ,a_k$
with a collection of functions that are more manageable. This will enable us to separate the polynomial functions from strongly non-polynomial ones. In addition, among the strongly non-polynomial functions, we have to isolate those that are sub-fractional, because they behave differently when we try to employ the Taylor expansion. This whole process will reduce Proposition 4.1 below to Lemma 4.2, which we will then proceed to establish.
$a_1,\ldots ,a_k$
with a collection of functions that are more manageable. This will enable us to separate the polynomial functions from strongly non-polynomial ones. In addition, among the strongly non-polynomial functions, we have to isolate those that are sub-fractional, because they behave differently when we try to employ the Taylor expansion. This whole process will reduce Proposition 4.1 below to Lemma 4.2, which we will then proceed to establish.
Following all these reductions, we use the Taylor expansion to substitute the strongly non-polynomial functions with polynomials in some small intervals. Now, this reduces the original problem to a quantitative equidistribution problem of finite polynomial sequences in a nilmanifold, although the coefficients of the polynomials vary depending on the underlying short interval. Finally, in step 3, we use the quantitative equidistribution results to show that averages of Lipschitz functions in the nilmanifold over these ‘variable’ polynomial sequences are very close to an integral over a subnilmanifold, which ultimately allows us to evaluate the limit of the initial averages.
We make one final reduction: let
![]() $a_1,\ldots ,a_k\in \mathcal {H}$
be functions as in the statement of Theorem 1.2. Passing to the product nilmanifold, we infer that our problem follows from the following statement.
$a_1,\ldots ,a_k\in \mathcal {H}$
be functions as in the statement of Theorem 1.2. Passing to the product nilmanifold, we infer that our problem follows from the following statement.
Proposition 4.1. Let
![]() $X=G/\Gamma $
be a nilmanifold,
$X=G/\Gamma $
be a nilmanifold,
![]() $b_1,\ldots ,b_k\in G$
are commuting elements and
$b_1,\ldots ,b_k\in G$
are commuting elements and
![]() $a_1,\ldots ,a_k\in \mathcal {H}$
have polynomial growth. Assume that there exists
$a_1,\ldots ,a_k\in \mathcal {H}$
have polynomial growth. Assume that there exists
![]() $\varepsilon>0$
, such that every function
$\varepsilon>0$
, such that every function
![]() $a\in \mathcal {L}(a_1,\ldots ,a_k)$
satisfies either equation (8) or equation (9). Then, for any
$a\in \mathcal {L}(a_1,\ldots ,a_k)$
satisfies either equation (8) or equation (9). Then, for any
![]() $x\in X$
and continuous function
$x\in X$
and continuous function
![]() $F:X\to \mathbb {C}$
, we have that the averages
$F:X\to \mathbb {C}$
, we have that the averages
converge.
Proof that Proposition 4.1 implies Theorem 1.2
We want to show that the averages
 $$ \begin{align*} \frac{1}{N}\sum_{i=1}^{N} f_1(b_1^{a_1(n)}x_1) \cdots f_k(b_k^{a_k(n)}x_k) \end{align*} $$
$$ \begin{align*} \frac{1}{N}\sum_{i=1}^{N} f_1(b_1^{a_1(n)}x_1) \cdots f_k(b_k^{a_k(n)}x_k) \end{align*} $$
converge for all
![]() $x_i\in X_i$
, where the nilmanifolds
$x_i\in X_i$
, where the nilmanifolds
![]() $X_i=G_i/\Gamma _i$
, the elements
$X_i=G_i/\Gamma _i$
, the elements
![]() $b_i$
and the functions
$b_i$
and the functions
![]() $a_i\in \mathcal {H}$
are as in the statement of part (ii) of Theorem 1.2. We define the continuous function F on the product nilmanifold
$a_i\in \mathcal {H}$
are as in the statement of part (ii) of Theorem 1.2. We define the continuous function F on the product nilmanifold
![]() $X_1\times \cdots \times X_k$
by the relation
$X_1\times \cdots \times X_k$
by the relation
We also denote by
![]() $\widetilde {b_i}$
the element on
$\widetilde {b_i}$
the element on
![]() $G_1\times \cdots \times G_k$
, whose ith coordinate is equal to
$G_1\times \cdots \times G_k$
, whose ith coordinate is equal to
![]() $b_i$
, while all of its other coordinates are equal to the respective identity element. Observe that the elements
$b_i$
, while all of its other coordinates are equal to the respective identity element. Observe that the elements
![]() $\widetilde {b_1},\ldots ,\widetilde {b_k}$
are pairwise commuting. Finally, let us also denote by x the point
$\widetilde {b_1},\ldots ,\widetilde {b_k}$
are pairwise commuting. Finally, let us also denote by x the point
![]() $(x_1,\ldots ,x_k)$
on the product
$(x_1,\ldots ,x_k)$
on the product
![]() $X_1\times \cdots \times X_k$
. Then, a simple computation implies that our initial average is equal to
$X_1\times \cdots \times X_k$
. Then, a simple computation implies that our initial average is equal to
and the claim now follows.
Now, we will reduce Proposition 4.1 to the following lemma.
Lemma 4.2. Let
![]() $G/\Gamma $
be a nilmanifold and suppose that
$G/\Gamma $
be a nilmanifold and suppose that
![]() $u_1,\ldots ,u_{s}$
are elements in G, such that
$u_1,\ldots ,u_{s}$
are elements in G, such that
In addition, assume that the nilmanifold
![]() $X'=\overline {u_1^{\mathbb {R}}\ldots u_{s}^{\mathbb {R}}\Gamma }$
can be represented as
$X'=\overline {u_1^{\mathbb {R}}\ldots u_{s}^{\mathbb {R}}\Gamma }$
can be represented as
![]() $G'/\Gamma '$
, where
$G'/\Gamma '$
, where
![]() $G'$
is connected, simply connected and contains all elements
$G'$
is connected, simply connected and contains all elements
![]() $u_1,\ldots ,u_{s}$
. Let
$u_1,\ldots ,u_{s}$
. Let
![]() $s_0,s$
be positive integers and define the sequence
$s_0,s$
be positive integers and define the sequence
![]() $v(n)$
$v(n)$
 $$ \begin{align} \prod_{i=1}^{s_0} u_i^{p_i(n)+x_i(n)} \prod_{i=s_0+1}^{s}u_i^{\widetilde{p}_i(n)+x_i(n)}, \end{align} $$
$$ \begin{align} \prod_{i=1}^{s_0} u_i^{p_i(n)+x_i(n)} \prod_{i=s_0+1}^{s}u_i^{\widetilde{p}_i(n)+x_i(n)}, \end{align} $$
where:
-
(a)
 $p_i,\widetilde {p}_j$
are polynomials with real coefficients, such that every non-trivial linear combination of the polynomials
$p_i,\widetilde {p}_j$
are polynomials with real coefficients, such that every non-trivial linear combination of the polynomials
 $\widetilde {p}_{s_0+1},\ldots ,\widetilde {p}_s$
is not an integer polynomial;
$\widetilde {p}_{s_0+1},\ldots ,\widetilde {p}_s$
is not an integer polynomial; -
(b) the functions
 $x_{i}$
are all strongly non-polynomial, the functions
$x_{i}$
are all strongly non-polynomial, the functions
 $x_1,\ldots ,x_{s_0}$
are not sub-fractional and have pairwise distinct growth rates and the functions
$x_1,\ldots ,x_{s_0}$
are not sub-fractional and have pairwise distinct growth rates and the functions
 $x_{s_0+1},\ldots ,x_s$
are sub-fractional.
$x_{s_0+1},\ldots ,x_s$
are sub-fractional.Then, for any Lipschitz function F on
 $X'$
with Lipschitz norm at most 1, the averages converge to the integral
$X'$
with Lipschitz norm at most 1, the averages converge to the integral $$ \begin{align*} \underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} F\bigg(\prod_{i=1}^{s_0} u_i^{p_i(n)+x_i(n)} \prod_{i=s_0+1}^{s}u_i^{\widetilde{p}_i(n)+x_i(n)}\Gamma'\bigg) \end{align*} $$
$$ \begin{align*} \underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} F\bigg(\prod_{i=1}^{s_0} u_i^{p_i(n)+x_i(n)} \prod_{i=s_0+1}^{s}u_i^{\widetilde{p}_i(n)+x_i(n)}\Gamma'\bigg) \end{align*} $$
 $\int _{X'}F \ dm_{X'}$
.
$\int _{X'}F \ dm_{X'}$
.
While the statement may seem relatively convoluted at first, the sequence
![]() $v(n)$
above has a convenient form, so that the Taylor approximation can be used directly.
$v(n)$
above has a convenient form, so that the Taylor approximation can be used directly.
First of all, we prove that Lemma 4.2 implies Proposition 4.1. We will rely on Lemma A.5 to make the required reductions on the Hardy field functions in the iterates and we will also use Lemma B.2 to get the equality equation (19), where
![]() $u_1,\ldots ,u_s$
will be some appropriate elements of the Lie group G (they will be products of powers of the elements
$u_1,\ldots ,u_s$
will be some appropriate elements of the Lie group G (they will be products of powers of the elements
![]() $b_i$
in Proposition 4.1).
$b_i$
in Proposition 4.1).
Proof that Lemma 4.2 implies Proposition 4.1
Applying Lemma A.5, we can find a basis
![]() ${f_1,\ldots ,f_s}$
for the set
${f_1,\ldots ,f_s}$
for the set
![]() $\mathcal {L}(a_1,\ldots ,a_k)$
of non-trivial linear combinations. The collection of functions
$\mathcal {L}(a_1,\ldots ,a_k)$
of non-trivial linear combinations. The collection of functions
![]() $f_1,\ldots ,f_s$
can be written in the form
$f_1,\ldots ,f_s$
can be written in the form
![]() $(g_1,\ldots ,g_m,h_1,\ldots ,h_{\ell })$
where
$(g_1,\ldots ,g_m,h_1,\ldots ,h_{\ell })$
where
![]() $g_i,h_{i}$
are as in Lemma A.5. We will not use this specific property until a little further below, so as to avoid cumbersome notation. Note that the fact that
$g_i,h_{i}$
are as in Lemma A.5. We will not use this specific property until a little further below, so as to avoid cumbersome notation. Note that the fact that
![]() $f_1,\ldots ,f_s$
form a basis indicates that the assumptions on the linear combinations of the
$f_1,\ldots ,f_s$
form a basis indicates that the assumptions on the linear combinations of the
![]() $a_1,\ldots ,a_k$
in the statement of Proposition 4.1 are now transferred to the functions
$a_1,\ldots ,a_k$
in the statement of Proposition 4.1 are now transferred to the functions
![]() $f_1,\ldots ,f_s$
.
$f_1,\ldots ,f_s$
.
If we write
 $$ \begin{align} a_i(t)=\sum_{j=1}^{s} c_{i,j}f_j(t) \end{align} $$
$$ \begin{align} a_i(t)=\sum_{j=1}^{s} c_{i,j}f_j(t) \end{align} $$
for some real numbers
![]() $c_{i,j}$
, then we can rewrite the average in equation (18) as
$c_{i,j}$
, then we can rewrite the average in equation (18) as
for some commuting elements
![]() $u_1,\ldots ,u_s\in G$
(here, the fact that the elements
$u_1,\ldots ,u_s\in G$
(here, the fact that the elements
![]() $b_1,\ldots ,b_k$
commute is required). We denote
$b_1,\ldots ,b_k$
commute is required). We denote
which is a sequence in G. We want to establish that the averages of the sequence
![]() $F(v(n)x)$
converge for all
$F(v(n)x)$
converge for all
![]() $x\in X$
and any continuous function F. If one of the functions
$x\in X$
and any continuous function F. If one of the functions
![]() $f_1,\ldots ,f_m$
is such that the limit
$f_1,\ldots ,f_m$
is such that the limit
![]() $\lim \nolimits _{t\to +\infty } f_i(t)$
is a real number (which can be the case when a linear combination of the original functions satisfies equation (9)), we can invoke the continuity of F to eliminate the corresponding term
$\lim \nolimits _{t\to +\infty } f_i(t)$
is a real number (which can be the case when a linear combination of the original functions satisfies equation (9)), we can invoke the continuity of F to eliminate the corresponding term
![]() $u_i^{f_i(n)}$
in the product and replace it by a constant. Hence, we may assume that all of the functions
$u_i^{f_i(n)}$
in the product and replace it by a constant. Hence, we may assume that all of the functions
![]() $f_1(t),\ldots ,f_s(t)$
go to
$f_1(t),\ldots ,f_s(t)$
go to
![]() $\pm \infty $
, as
$\pm \infty $
, as
![]() $t\to +\infty $
.
$t\to +\infty $
.
Now we use the particular structure of the functions
![]() $f_1,\ldots ,f_s$
. The statement of Lemma A.5 implies that the collection of functions
$f_1,\ldots ,f_s$
. The statement of Lemma A.5 implies that the collection of functions
![]() $f_1,\ldots ,f_s$
has the form
$f_1,\ldots ,f_s$
has the form
![]() $(g_1,\ldots ,g_m,h_1,\ldots ,h_{\ell })$
(clearly,
$(g_1,\ldots ,g_m,h_1,\ldots ,h_{\ell })$
(clearly,
![]() $m+\ell =s$
) such that the functions
$m+\ell =s$
) such that the functions
![]() $g_i$
can be written in the form
$g_i$
can be written in the form
![]() $p_i(t)+x_i(t)$
, where the functions
$p_i(t)+x_i(t)$
, where the functions
![]() $x_1(t),\ldots ,x_{m}(t)$
are strongly non-polynomial and have pairwise distinct (and non-trivial) growth rates, while the functions
$x_1(t),\ldots ,x_{m}(t)$
are strongly non-polynomial and have pairwise distinct (and non-trivial) growth rates, while the functions
![]() $h_i$
can be written in the form
$h_i$
can be written in the form
![]() $\widetilde {p}_i(t)+y_i(t)$
, where
$\widetilde {p}_i(t)+y_i(t)$
, where
![]() $y_i(t)$
converges to 0. Here,
$y_i(t)$
converges to 0. Here,
![]() $p_i$
and
$p_i$
and
![]() $\widetilde {p}_i$
are polynomials with real coefficients.
$\widetilde {p}_i$
are polynomials with real coefficients.
We may rearrange the functions
![]() $f_i$
so that
$f_i$
so that
![]() $f_i=g_i$
for all
$f_i=g_i$
for all
![]() $1\leq i\leq m$
and
$1\leq i\leq m$
and
![]() $f_j=h_{j-m}$
for each
$f_j=h_{j-m}$
for each
![]() $m+1\leq j\leq s$
. Rewrite the sequence
$m+1\leq j\leq s$
. Rewrite the sequence
![]() $v(n)$
as
$v(n)$
as
 $$ \begin{align*} v(n)=\prod_{i=1}^{m}u_i^{g_i(n)}\cdot \prod_{i=1}^{\ell} u_{m+i}^{h_i(n)}=\prod_{i=1}^{m}u_i^{p_i(n)+x_i(n)}\cdot \prod_{i=1}^{\ell} w_i^{\widetilde{p}_i(n)+y_i(n)}, \end{align*} $$
$$ \begin{align*} v(n)=\prod_{i=1}^{m}u_i^{g_i(n)}\cdot \prod_{i=1}^{\ell} u_{m+i}^{h_i(n)}=\prod_{i=1}^{m}u_i^{p_i(n)+x_i(n)}\cdot \prod_{i=1}^{\ell} w_i^{\widetilde{p}_i(n)+y_i(n)}, \end{align*} $$
where we use the notation
![]() $w_i$
for the element
$w_i$
for the element
![]() $u_{i+m}$
in the last equality. Without loss of generality, assume that
$u_{i+m}$
in the last equality. Without loss of generality, assume that
First, we need to distinguish between the sub-fractional functions and the ‘fast’ growing functions among the functions
![]() $x_i(t)$
(this will be important later when we use the polynomial expansion). Thus, let
$x_i(t)$
(this will be important later when we use the polynomial expansion). Thus, let
![]() $0\leq s_0\leq m$
be a natural number such that
$0\leq s_0\leq m$
be a natural number such that
![]() $x_{s_0}(t)\gg t^{\varepsilon }$
for some
$x_{s_0}(t)\gg t^{\varepsilon }$
for some
![]() $\varepsilon>0$
, while
$\varepsilon>0$
, while
![]() $x_{s_0+1}$
is a sub-fractional function. This also implies that all the functions
$x_{s_0+1}$
is a sub-fractional function. This also implies that all the functions
![]() $x_{i}$
for i satisfying
$x_{i}$
for i satisfying
![]() $\ s_0+1\leq i\leq m$
are sub-fractional since we have arranged the functions so that their growth rates are in descending order.
$\ s_0+1\leq i\leq m$
are sub-fractional since we have arranged the functions so that their growth rates are in descending order.
Once again, we rewrite the sequence
![]() $v(n)$
in the form
$v(n)$
in the form
 $$ \begin{align*} v(n)= \prod_{i=1}^{s_0} u_i^{p_i(n)+x_i(n)} \prod_{i=s_0+1}^{m} u_i^{p_i(n)+x_i(n)} \ \prod_{i=1}^{\ell}\ w_i^{\widetilde{p}_i(n)+y_i(n)}. \end{align*} $$
$$ \begin{align*} v(n)= \prod_{i=1}^{s_0} u_i^{p_i(n)+x_i(n)} \prod_{i=s_0+1}^{m} u_i^{p_i(n)+x_i(n)} \ \prod_{i=1}^{\ell}\ w_i^{\widetilde{p}_i(n)+y_i(n)}. \end{align*} $$
Because the function F is continuous, we can discard the functions
![]() $y_1,\ldots ,y_{\ell }$
, since they all converge to zero. The hypotheses in equations (8) and (9) on the linear combinations of the remaining functions in the exponents continue to hold. Indeed, this can be seen by noting that equations (8) and (9) still hold when replacing one of the functions (say
$y_1,\ldots ,y_{\ell }$
, since they all converge to zero. The hypotheses in equations (8) and (9) on the linear combinations of the remaining functions in the exponents continue to hold. Indeed, this can be seen by noting that equations (8) and (9) still hold when replacing one of the functions (say
![]() $a_1$
) by a function of the form
$a_1$
) by a function of the form
![]() $a_1(t)+e(t)$
, with
$a_1(t)+e(t)$
, with
![]() $e(t)\to 0$
. Consequently, we can redefine
$e(t)\to 0$
. Consequently, we can redefine
![]() $v(n)$
to be the sequence
$v(n)$
to be the sequence
 $$ \begin{align*} v(n)= \prod_{i=1}^{s_0} u_i^{p_i(n)+x_i(n)} \prod_{i=s_0+1}^{m} u_i^{p_i(n)+x_i(n)} \ \prod_{i=1}^{\ell}\ w_i^{\widetilde{p}_i(n)}. \end{align*} $$
$$ \begin{align*} v(n)= \prod_{i=1}^{s_0} u_i^{p_i(n)+x_i(n)} \prod_{i=s_0+1}^{m} u_i^{p_i(n)+x_i(n)} \ \prod_{i=1}^{\ell}\ w_i^{\widetilde{p}_i(n)}. \end{align*} $$
We will now reduce our problem to the case that the polynomials
![]() $\widetilde {p}_1(t),\ldots ,\widetilde {p}_{\ell }(t)$
are linearly independent. Due to our hypothesis (namely equations (8),(9)), every non-trivial linear combination of the functions
$\widetilde {p}_1(t),\ldots ,\widetilde {p}_{\ell }(t)$
are linearly independent. Due to our hypothesis (namely equations (8),(9)), every non-trivial linear combination of the functions
![]() $\widetilde {p}_1(t),\ldots ,\widetilde {p}_{\ell }(t)$
must satisfy either equation (8) or equation (9). Thus, every linear combination of the polynomials
$\widetilde {p}_1(t),\ldots ,\widetilde {p}_{\ell }(t)$
must satisfy either equation (8) or equation (9). Thus, every linear combination of the polynomials
![]() $\widetilde {p}_1(t),\ldots ,\widetilde {p}_{\ell }(t)$
is not a polynomial with integer coefficients unless it is the zero polynomial. If the second case is true, there exist
$\widetilde {p}_1(t),\ldots ,\widetilde {p}_{\ell }(t)$
is not a polynomial with integer coefficients unless it is the zero polynomial. If the second case is true, there exist
![]() $c_1,\ldots ,c_{\ell -1}\in \mathbb {R}$
such that
$c_1,\ldots ,c_{\ell -1}\in \mathbb {R}$
such that
Then, we have
 $$ \begin{align*}\prod_{i=1}^{\ell} w_{i}^{\widetilde{p}_i(n)}=\prod_{i=1}^{\ell-1}(w_{i}w_{\ell}^{c_i})^{\widetilde{p}_i(n)}. \end{align*} $$
$$ \begin{align*}\prod_{i=1}^{\ell} w_{i}^{\widetilde{p}_i(n)}=\prod_{i=1}^{\ell-1}(w_{i}w_{\ell}^{c_i})^{\widetilde{p}_i(n)}. \end{align*} $$
If the polynomials
![]() $\widetilde {p}_1,\ldots ,\widetilde {p}_{\ell -1}$
are linearly independent, then we are done. Otherwise, we proceed similarly to eliminate
$\widetilde {p}_1,\ldots ,\widetilde {p}_{\ell -1}$
are linearly independent, then we are done. Otherwise, we proceed similarly to eliminate
![]() $\widetilde {p}_{\ell -1}$
. After a finite number of steps, we will reach a collection of linearly independent polynomials.
$\widetilde {p}_{\ell -1}$
. After a finite number of steps, we will reach a collection of linearly independent polynomials.
In view of the above, we are allowed to assume that
![]() $\widetilde {p}_1,\ldots ,\widetilde {p}_{\ell }$
are linearly independent. Now, we show that we can reduce to the case that the polynomials
$\widetilde {p}_1,\ldots ,\widetilde {p}_{\ell }$
are linearly independent. Now, we show that we can reduce to the case that the polynomials
![]() $p_{s_0+1},\ldots , p_{m},\widetilde {p}_{1},\ldots , \widetilde {p}_{\ell }$
. Indeed, the linear independence assumption on the polynomials
$p_{s_0+1},\ldots , p_{m},\widetilde {p}_{1},\ldots , \widetilde {p}_{\ell }$
. Indeed, the linear independence assumption on the polynomials
![]() $\widetilde {p}_1,\ldots , \widetilde {p}_{\ell }$
implies that the polynomials
$\widetilde {p}_1,\ldots , \widetilde {p}_{\ell }$
implies that the polynomials
![]() $p_{s_0+1},\ldots ,p_m,\widetilde {p}_1,\ldots ,\widetilde {p}_{\ell }$
are linearly independent. To see how this works, observe that if there are real numbers
$p_{s_0+1},\ldots ,p_m,\widetilde {p}_1,\ldots ,\widetilde {p}_{\ell }$
are linearly independent. To see how this works, observe that if there are real numbers
![]() $c_i,d_j$
such that
$c_i,d_j$
such that
 $$ \begin{align*}\sum_{i=1}^{m-s_0}c_ip_{s_0+i}+\sum_{i=1}^{\ell}d_ip^{\prime}_i=0,\end{align*} $$
$$ \begin{align*}\sum_{i=1}^{m-s_0}c_ip_{s_0+i}+\sum_{i=1}^{\ell}d_ip^{\prime}_i=0,\end{align*} $$
then the function
 $$ \begin{align*} \sum_{i=1}^{m-s_0}c_i(p_{s_0+i}+x_{s_0+i})+\sum_{i=1}^{\ell}d_i\widetilde{p}_i= \sum_{i=1}^{m-s_0}c_ix_{s_0+i} \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{m-s_0}c_i(p_{s_0+i}+x_{s_0+i})+\sum_{i=1}^{\ell}d_i\widetilde{p}_i= \sum_{i=1}^{m-s_0}c_ix_{s_0+i} \end{align*} $$
is a sub-fractional function that does not converge to 0, since the functions
![]() $x_{s_0+i}$
are sub-fractional and have pairwise distinct growth rates. This contradicts our hypothesis (specifically equation (8)) and our claim follows.
$x_{s_0+i}$
are sub-fractional and have pairwise distinct growth rates. This contradicts our hypothesis (specifically equation (8)) and our claim follows.
In conclusion, we see that the sequence
![]() $v(n)$
can be written in the form
$v(n)$
can be written in the form
 $$ \begin{align} \prod_{i=1}^{s_0} u_i^{p_i(n)+x_i(n)} \prod_{i=s_0+1}^{m}u_i^{p_i(n)+x_i(n)} \prod_{i=1}^{\ell}w_i^{\widetilde{p}_i(n)}, \end{align} $$
$$ \begin{align} \prod_{i=1}^{s_0} u_i^{p_i(n)+x_i(n)} \prod_{i=s_0+1}^{m}u_i^{p_i(n)+x_i(n)} \prod_{i=1}^{\ell}w_i^{\widetilde{p}_i(n)}, \end{align} $$
where the functions
![]() $x_{i}$
are strongly non-polynomial with distinct growth rates, the functions
$x_{i}$
are strongly non-polynomial with distinct growth rates, the functions
![]() $x_1,\ldots ,x_{s_0}$
are not sub-fractional, the functions
$x_1,\ldots ,x_{s_0}$
are not sub-fractional, the functions
![]() $x_{s_0+1},\ldots ,x_s$
are sub-fractional and every non-trivial linear combination of the polynomials
$x_{s_0+1},\ldots ,x_s$
are sub-fractional and every non-trivial linear combination of the polynomials
![]() $p_{s_0+1},\ldots ,p_m,\widetilde {p}_1,\ldots ,\widetilde {p}_{\ell }$
is not an integer polynomial. We also recall that we have arranged the functions
$p_{s_0+1},\ldots ,p_m,\widetilde {p}_1,\ldots ,\widetilde {p}_{\ell }$
is not an integer polynomial. We also recall that we have arranged the functions
![]() $x_i$
to be in decreasing order with respect to their growth rates.
$x_i$
to be in decreasing order with respect to their growth rates.
We can combine the last two factors of this product into one factor to simplify our problem a bit more. More specifically, we can rewrite the sequence
![]() $v(n)$
in the form (we make some mild modifications in our notation here)
$v(n)$
in the form (we make some mild modifications in our notation here)
 $$ \begin{align} v(n)=\prod_{i=1}^{s_0} u_i^{p_i(n)+x_i(n)} \prod_{i=s_0+1}^{s}u_i^{\widetilde{p}_i(n)+x_i(n)}, \end{align} $$
$$ \begin{align} v(n)=\prod_{i=1}^{s_0} u_i^{p_i(n)+x_i(n)} \prod_{i=s_0+1}^{s}u_i^{\widetilde{p}_i(n)+x_i(n)}, \end{align} $$
where
![]() $s=m+l$
,
$s=m+l$
,
![]() $p_i,\widetilde {p}_j$
are real polynomials, the functions
$p_i,\widetilde {p}_j$
are real polynomials, the functions
![]() $x_{i}$
are strongly non-polynomial with distinct growth rates,
$x_{i}$
are strongly non-polynomial with distinct growth rates,
![]() $x_1,\ldots ,x_{s_0}$
are not sub-fractional,
$x_1,\ldots ,x_{s_0}$
are not sub-fractional,
![]() $x_{s_0+1},\ldots ,x_s$
are sub-fractional and every non-trivial linear combination of the polynomials
$x_{s_0+1},\ldots ,x_s$
are sub-fractional and every non-trivial linear combination of the polynomials
![]() $\widetilde {p}_{i}$
is not an integer polynomial. Namely, our functions satisfy hypotheses (a) and (b) of Lemma 4.2.
$\widetilde {p}_{i}$
is not an integer polynomial. Namely, our functions satisfy hypotheses (a) and (b) of Lemma 4.2.
To establish our assertion, it suffices to show that the sequence
![]() $v(n)x$
(where
$v(n)x$
(where
![]() $v(n)$
is as in equation (24)) is equidistributed on the nilmanifold
$v(n)$
is as in equation (24)) is equidistributed on the nilmanifold
![]() $X'=\overline {u_1^{\mathbb {R}}\cdots u_s^{\mathbb {R}}x}$
for any
$X'=\overline {u_1^{\mathbb {R}}\cdots u_s^{\mathbb {R}}x}$
for any
![]() $x\in X$
. We will prove this in the case
$x\in X$
. We will prove this in the case
![]() $x=\Gamma $
since the general case follows from this using the change of base point trick that we discuss in Appendix B (see §B.1.2). In addition, we can invoke Lemma B.2 to find a real number
$x=\Gamma $
since the general case follows from this using the change of base point trick that we discuss in Appendix B (see §B.1.2). In addition, we can invoke Lemma B.2 to find a real number
![]() $s_0$
, such that
$s_0$
, such that
![]() $X'=\overline {(u_1^{s_0})^{\mathbb {Z}}\ldots (u_s^{s_0})^{\mathbb {Z}}\Gamma }$
. Replacing the functions
$X'=\overline {(u_1^{s_0})^{\mathbb {Z}}\ldots (u_s^{s_0})^{\mathbb {Z}}\Gamma }$
. Replacing the functions
![]() $p_i(t)+x_i(t)$
(
$p_i(t)+x_i(t)$
(
![]() $1\leq i\leq s_0$
) by the functions
$1\leq i\leq s_0$
) by the functions
![]() $(p_i(t)+x_i(t))/s_0$
and
$(p_i(t)+x_i(t))/s_0$
and
![]() $\widetilde {p}_i(t)+x_i(t)$
(
$\widetilde {p}_i(t)+x_i(t)$
(
![]() $s_0+1\leq i\leq s$
) by
$s_0+1\leq i\leq s$
) by
![]() $(\widetilde {p}_i(t)+x_i(t))/s_0$
(the assumptions on the linear combinations of the functions remain unaffected), we can reduce our problem to the case that
$(\widetilde {p}_i(t)+x_i(t))/s_0$
(the assumptions on the linear combinations of the functions remain unaffected), we can reduce our problem to the case that
![]() $X'=\overline {u_1^{\mathbb {Z}}\ldots u_s^{\mathbb {Z}}\Gamma }$
.
$X'=\overline {u_1^{\mathbb {Z}}\ldots u_s^{\mathbb {Z}}\Gamma }$
.
We want to show that for any continuous function F from
![]() $X'=G'/\Gamma '$
(
$X'=G'/\Gamma '$
(
![]() $G'$
is connected, simply connected and
$G'$
is connected, simply connected and
![]() $\Gamma '$
is a uniform subgroup), the averages
$\Gamma '$
is a uniform subgroup), the averages
converge to the integral
![]() $\int _{X'}F \ dm_{X'}$
. Since Lipschitz functions are dense in the space
$\int _{X'}F \ dm_{X'}$
. Since Lipschitz functions are dense in the space
![]() $C(X')$
, we may assume that F is Lipschitz continuous. In addition, we may assume after rescaling that
$C(X')$
, we may assume that F is Lipschitz continuous. In addition, we may assume after rescaling that
![]() $\lVert F \rVert _{\text {Lip}(X')}\leq 1$
. Now, our claim follows immediately from Lemma 4.2.
$\lVert F \rVert _{\text {Lip}(X')}\leq 1$
. Now, our claim follows immediately from Lemma 4.2.
In the following part, we will prove Lemma 4.2. We divide the proof into two steps. During step 1, we will approximate the functions
![]() $x_1,\ldots ,x_s$
by polynomials in a suitable short interval. Our goal is to reach an average over a short interval of the form
$x_1,\ldots ,x_s$
by polynomials in a suitable short interval. Our goal is to reach an average over a short interval of the form
![]() $[N, N+L(N)]$
of a sequence of the form
$[N, N+L(N)]$
of a sequence of the form
![]() $F(g(n)x)$
, where F is Lipschitz and
$F(g(n)x)$
, where F is Lipschitz and
![]() $g(n)$
is a polynomial sequence on the nilmanifold
$g(n)$
is a polynomial sequence on the nilmanifold
![]() $X'$
(the polynomial sequence will vary with the parameter N). This will be ensured by Proposition A.4. In step 2, we will use Theorem F to deduce that these averages are close to the integral of F for large values of N.
$X'$
(the polynomial sequence will vary with the parameter N). This will be ensured by Proposition A.4. In step 2, we will use Theorem F to deduce that these averages are close to the integral of F for large values of N.
All the reductions above allow us to write
![]() $v(n)$
in a form that will be appropriate for the application of the quantitative equidistribution theorem (after we perform the Taylor expansion). When we apply the Taylor expansion in the first step, the functions
$v(n)$
in a form that will be appropriate for the application of the quantitative equidistribution theorem (after we perform the Taylor expansion). When we apply the Taylor expansion in the first step, the functions
![]() $x_{s_0+1},\ldots ,x_{s}$
will become approximately constant and thus the desired equidistribution will be mainly ‘affected’ by the polynomials
$x_{s_0+1},\ldots ,x_{s}$
will become approximately constant and thus the desired equidistribution will be mainly ‘affected’ by the polynomials
![]() $\widetilde {p}_{s_0+1},\ldots ,\widetilde {p}_s$
. However, the functions
$\widetilde {p}_{s_0+1},\ldots ,\widetilde {p}_s$
. However, the functions
![]() $x_1,\ldots ,x_{s_0}$
will play a meaningful role in the equidistribution of our sequence. In particular, the presence of the functions
$x_1,\ldots ,x_{s_0}$
will play a meaningful role in the equidistribution of our sequence. In particular, the presence of the functions
![]() $x_1,\ldots ,x_{s_0}$
will imply ‘closeness’ of our averages to the integral of the Lipschitz function F, unless the projections of the elements
$x_1,\ldots ,x_{s_0}$
will imply ‘closeness’ of our averages to the integral of the Lipschitz function F, unless the projections of the elements
![]() $u_1,\ldots , u_{s_0}$
on the horizontal torus are zero. In this second case, condition (a) on the polynomials completes the proof. Lastly, the ‘linear independence’ condition of the polynomials
$u_1,\ldots , u_{s_0}$
on the horizontal torus are zero. In this second case, condition (a) on the polynomials completes the proof. Lastly, the ‘linear independence’ condition of the polynomials
![]() $\widetilde {p}_{s_0+1},\ldots ,\widetilde {p}_s$
guarantees that the projection of the sequence
$\widetilde {p}_{s_0+1},\ldots ,\widetilde {p}_s$
guarantees that the projection of the sequence
![]() $v(n)$
on
$v(n)$
on
![]() $X'$
will be equidistributed on the entire nilmanifold
$X'$
will be equidistributed on the entire nilmanifold
![]() $\overline {u_1^{\mathbb {R}}\cdots u_{s}^{\mathbb {R}}\Gamma }$
, since otherwise, we would need to pass to some subnilmanifold to guarantee equidistribution (and to an appropriate arithmetic progression).
$\overline {u_1^{\mathbb {R}}\cdots u_{s}^{\mathbb {R}}\Gamma }$
, since otherwise, we would need to pass to some subnilmanifold to guarantee equidistribution (and to an appropriate arithmetic progression).
Proof of Lemma 4.2
Step 1. Approximating by polynomials. Let
![]() $L(t)$
be a sub-linear function with
$L(t)$
be a sub-linear function with
![]() $\lim \nolimits _{t\to +\infty }L(t)=+\infty $
that we will determine later. It suffices to show that the sequence of the averages
$\lim \nolimits _{t\to +\infty }L(t)=+\infty $
that we will determine later. It suffices to show that the sequence of the averages
converges to
![]() $\int _{X'}F \ d m_{X'}$
, since the conclusion would follow from Lemma 3.1. Reordering if necessary, we assume again that
$\int _{X'}F \ d m_{X'}$
, since the conclusion would follow from Lemma 3.1. Reordering if necessary, we assume again that
Let r be a very large natural number compared to the degrees of the polynomials
![]() $p_i,\widetilde {p}_j$
and the degrees of the functions
$p_i,\widetilde {p}_j$
and the degrees of the functions
![]() $x_i(t)$
. If r is sufficiently large, we have that
$x_i(t)$
. If r is sufficiently large, we have that
![]() $x_i^{(r)}(t)=o_t(1)$
for all
$x_i^{(r)}(t)=o_t(1)$
for all
![]() $i\in \{1,\ldots ,s_0\}$
. Assuming again that r is sufficiently large, then for any function
$i\in \{1,\ldots ,s_0\}$
. Assuming again that r is sufficiently large, then for any function
![]() $L(t)$
that satisfies
$L(t)$
that satisfies
for some
![]() $\varepsilon '>0$
and all
$\varepsilon '>0$
and all
![]() $i\in {1,\ldots ,s_0}$
, we have that for each
$i\in {1,\ldots ,s_0}$
, we have that for each
![]() $ i\in \{1,\ldots ,s_0\}$
, there is a unique natural number
$ i\in \{1,\ldots ,s_0\}$
, there is a unique natural number
![]() $k_i\geq r$
so that the sub-class
$k_i\geq r$
so that the sub-class
![]() $S(x_i,k_i)$
contains the function
$S(x_i,k_i)$
contains the function
![]() $L(t)$
(this follows from Proposition A.3). The fact that the function
$L(t)$
(this follows from Proposition A.3). The fact that the function
![]() $L(t)$
belongs to
$L(t)$
belongs to
![]() $S(x_i,k_i)$
indicates that we have the relations
$S(x_i,k_i)$
indicates that we have the relations
We can guarantee that the numbers
![]() $k_i$
are also very large compared to the degrees of the polynomials
$k_i$
are also very large compared to the degrees of the polynomials
![]() $p_{j},\widetilde {p}_{j'}$
by enlarging the number r in the beginning. (For example, assuming that
$p_{j},\widetilde {p}_{j'}$
by enlarging the number r in the beginning. (For example, assuming that
![]() $k_i$
is at least 10 times as large as the maximal degree appearing among the polynomials
$k_i$
is at least 10 times as large as the maximal degree appearing among the polynomials
![]() $p_i,\widetilde {p}_j$
and 10 times as large as the number s of all existing polynomials would suffice for our arguments.)
$p_i,\widetilde {p}_j$
and 10 times as large as the number s of all existing polynomials would suffice for our arguments.)
We use the Taylor expansion for the functions
![]() $x_1(t),\ldots ,x_{s_0}(t)$
to write
$x_1(t),\ldots ,x_{s_0}(t)$
to write
 $$ \begin{align} x_i(N+h)=x_i(N)+\cdots +\frac{x_{i}^{k_i}(N)h^k}{k_i !}+o_N(1)= q_{i,N}(h)+o_N(1) \end{align} $$
$$ \begin{align} x_i(N+h)=x_i(N)+\cdots +\frac{x_{i}^{k_i}(N)h^k}{k_i !}+o_N(1)= q_{i,N}(h)+o_N(1) \end{align} $$
for
![]() $0\leq h\leq L(N)$
(for the explanation of the
$0\leq h\leq L(N)$
(for the explanation of the
![]() $o_N(1)$
term, see the discussion after Proposition A.2). If, however, we have
$o_N(1)$
term, see the discussion after Proposition A.2). If, however, we have
![]() $i>s_0$
(namely, in the case where the function
$i>s_0$
(namely, in the case where the function
![]() $x_i$
is sub-fractional), then
$x_i$
is sub-fractional), then
In addition, we denote
![]() $p_{i,N}(h)=p_i(N+h)$
and similarly
$p_{i,N}(h)=p_i(N+h)$
and similarly
![]() $\widetilde {p}_{i,N}(h)=\widetilde {p}_i(N+h)$
for every admissible value of i. Thus, we rewrite the expression in equation (25) as
$\widetilde {p}_{i,N}(h)=\widetilde {p}_i(N+h)$
for every admissible value of i. Thus, we rewrite the expression in equation (25) as
 $$ \begin{align} \underset{0\leq h\leq L(N)}{\operatorname*{\mathrm{\mathbb{E}}}} F(w_N \prod_{i=1}^{s_0} u_i^{q_{i,N}(h)+p_{i,N}(h)} \prod_{i=s_0+1}^{s} u_i^{\widetilde{p}_{i,N}(h)} \Gamma'), \end{align} $$
$$ \begin{align} \underset{0\leq h\leq L(N)}{\operatorname*{\mathrm{\mathbb{E}}}} F(w_N \prod_{i=1}^{s_0} u_i^{q_{i,N}(h)+p_{i,N}(h)} \prod_{i=s_0+1}^{s} u_i^{\widetilde{p}_{i,N}(h)} \Gamma'), \end{align} $$
where we discarded the
![]() $o_N(1)$
terms, because F is continuous. Here,
$o_N(1)$
terms, because F is continuous. Here,
![]() $w_N=\prod _{i=s_0+1}^{s}u_i^{x_i(N)}$
but the explicit form of this term will not concern us, since we will only require that the element
$w_N=\prod _{i=s_0+1}^{s}u_i^{x_i(N)}$
but the explicit form of this term will not concern us, since we will only require that the element
![]() $w_N$
belongs to the underlying group
$w_N$
belongs to the underlying group
![]() $G'$
defining the nilmanifold
$G'$
defining the nilmanifold
![]() $X'=\overline {u_1^{\mathbb {R}}\cdots u_s^{\mathbb {R}}\Gamma }$
.
$X'=\overline {u_1^{\mathbb {R}}\cdots u_s^{\mathbb {R}}\Gamma }$
.
In conclusion, we have reduced our problem to showing that given the nilmanifold
![]() $X'=\overline {u_1^{\mathbb {R}}\cdots u_s^{\mathbb {R}}\Gamma }$
(which is also equal to
$X'=\overline {u_1^{\mathbb {R}}\cdots u_s^{\mathbb {R}}\Gamma }$
(which is also equal to
![]() $\overline {u_1^{\mathbb {Z}}\cdots u_s^{\mathbb {Z}}\Gamma }$
), the averages in equation (29) converge. Here, the polynomials
$\overline {u_1^{\mathbb {Z}}\cdots u_s^{\mathbb {Z}}\Gamma }$
), the averages in equation (29) converge. Here, the polynomials
![]() $q_{i, N}$
are defined in equation (27) (they are essentially the Taylor polynomials of the Hardy field functions
$q_{i, N}$
are defined in equation (27) (they are essentially the Taylor polynomials of the Hardy field functions
![]() $x_i$
), while the polynomials
$x_i$
), while the polynomials
![]() $p_{i, N},\widetilde {p}_{j, N}$
were defined by the relations
$p_{i, N},\widetilde {p}_{j, N}$
were defined by the relations
![]() $p_{i, N}=p_i(N+h) \text { and }\ \widetilde {p}_{j, N}=\widetilde {p}_j(N+h)$
, where the
$p_{i, N}=p_i(N+h) \text { and }\ \widetilde {p}_{j, N}=\widetilde {p}_j(N+h)$
, where the
![]() $p_i,\widetilde {p}_j$
are polynomials with real coefficients. We also recall that the polynomials
$p_i,\widetilde {p}_j$
are polynomials with real coefficients. We also recall that the polynomials
![]() $\widetilde {p}_i$
are such that every non-trivial linear combination of them is not an integer polynomial. Under all these assumptions, we will show that the polynomial sequence (restricted to the range
$\widetilde {p}_i$
are such that every non-trivial linear combination of them is not an integer polynomial. Under all these assumptions, we will show that the polynomial sequence (restricted to the range
![]() $0\leq h\leq L(N)$
) inside the function F is
$0\leq h\leq L(N)$
) inside the function F is
![]() $\delta $
-equidistributed for N sufficiently large in the following step. We remark that the growth conditions in equation (26) imposed on the function
$\delta $
-equidistributed for N sufficiently large in the following step. We remark that the growth conditions in equation (26) imposed on the function
![]() $L(t)$
will also play a crucial role in this.
$L(t)$
will also play a crucial role in this.
Step 2. Using the quantitative equidistribution theorem. Let
![]() $Z\cong \mathbb {T}^{d}$
be the horizontal torus of the nilmanifold
$Z\cong \mathbb {T}^{d}$
be the horizontal torus of the nilmanifold
![]() $X'=\overline {u_1^{\mathbb {R}}\cdots u_s^{\mathbb {R}}\Gamma }$
and let
$X'=\overline {u_1^{\mathbb {R}}\cdots u_s^{\mathbb {R}}\Gamma }$
and let
![]() $\pi :X'\to Z$
denote the projection map. Let
$\pi :X'\to Z$
denote the projection map. Let
![]() $\delta>0$
be sufficiently small (in the sense that Theorem F is applicable). We assert that the finite polynomial sequence
$\delta>0$
be sufficiently small (in the sense that Theorem F is applicable). We assert that the finite polynomial sequence
 $$ \begin{align} \bigg( \prod_{i=1}^{s_0} u_i^{q_{i,N}(h)+p_{i,N}(h)} \prod_{i=s_0+1}^{s} u_i^{\widetilde{p}_{i,N}(h)} \Gamma' \bigg)_{0\leq h\leq L(N)} \end{align} $$
$$ \begin{align} \bigg( \prod_{i=1}^{s_0} u_i^{q_{i,N}(h)+p_{i,N}(h)} \prod_{i=s_0+1}^{s} u_i^{\widetilde{p}_{i,N}(h)} \Gamma' \bigg)_{0\leq h\leq L(N)} \end{align} $$
is
![]() $\delta $
-equidistributed on the nilmanifold
$\delta $
-equidistributed on the nilmanifold
![]() $X'$
for N sufficiently large. If the claim does not hold for a natural number N, then by Theorem F, there exists a real number
$X'$
for N sufficiently large. If the claim does not hold for a natural number N, then by Theorem F, there exists a real number
![]() $M>0$
and a non-trivial horizontal character
$M>0$
and a non-trivial horizontal character
![]() $\chi _N$
of modulus
$\chi _N$
of modulus
![]() $\leq M$
such that
$\leq M$
such that
 $$ \begin{align} \bigg\lVert \chi_N\circ \pi \bigg( \prod_{i=1}^{s_0} u_i^{q_{i,N}(h)+p_{i,N}(h)} \prod_{i=s_0+1}^{s} u_i^{\widetilde{p}_{i,N}(h)} \Gamma'\bigg) \bigg\rVert_{C^{\infty}[L(N)]}\leq M. \end{align} $$
$$ \begin{align} \bigg\lVert \chi_N\circ \pi \bigg( \prod_{i=1}^{s_0} u_i^{q_{i,N}(h)+p_{i,N}(h)} \prod_{i=s_0+1}^{s} u_i^{\widetilde{p}_{i,N}(h)} \Gamma'\bigg) \bigg\rVert_{C^{\infty}[L(N)]}\leq M. \end{align} $$
(The constant M depends only on
![]() $\delta $
, the nilmanifold
$\delta $
, the nilmanifold
![]() $X'$
as well as the degrees of the polynomials
$X'$
as well as the degrees of the polynomials
![]() $q_i,p_i$
, which are all fixed in our arguments. The central property we need is that it is independent of the variable N.) Thus, if our prior assertion fails, then the above relation would hold for infinitely many
$q_i,p_i$
, which are all fixed in our arguments. The central property we need is that it is independent of the variable N.) Thus, if our prior assertion fails, then the above relation would hold for infinitely many
![]() $N\in \mathbb {N}$
.
$N\in \mathbb {N}$
.
Our first goal is to eliminate the dependence of the characters
![]() $\chi _N$
on the variable N. Note that the function
$\chi _N$
on the variable N. Note that the function
![]() $\chi _N\circ \pi $
is a character on
$\chi _N\circ \pi $
is a character on
![]() $\mathbb {T}^d$
of modulus
$\mathbb {T}^d$
of modulus
![]() $\leq M$
and, thus, has the form
$\leq M$
and, thus, has the form
for
![]() $k_{i,N}\in \mathbb {Z} $
with
$k_{i,N}\in \mathbb {Z} $
with
![]() $|k_{1,N}|+\cdots +|k_{d,N}|\leq M$
. We also write
$|k_{1,N}|+\cdots +|k_{d,N}|\leq M$
. We also write
![]() $\pi (u_i)= (u_{i,1},\ldots ,u_{i,d})$
for the projections of the elements
$\pi (u_i)= (u_{i,1},\ldots ,u_{i,d})$
for the projections of the elements
![]() $u_i$
on the horizontal torus. Then, a straightforward computation allows us to rewrite equation (31) as
$u_i$
on the horizontal torus. Then, a straightforward computation allows us to rewrite equation (31) as
 $$ \begin{align} &\bigg\lVert e\bigg(\sum_{i=1}^{s_0}(q_{i,N}(h)+p_{i,N}(h))(k_{1,N}u_{i,1}+\cdots+ k_{d,N}u_{i,d})\nonumber\\ &\quad+\sum_{i=s_0+1}^{s}(\widetilde{p}_{i,N}(h))(k_{1,N}u_{i,1}+\cdots+ k_{d,N}u_{i,d})\bigg) \bigg\rVert_{C^{\infty}[L(N)]}\leq M. \end{align} $$
$$ \begin{align} &\bigg\lVert e\bigg(\sum_{i=1}^{s_0}(q_{i,N}(h)+p_{i,N}(h))(k_{1,N}u_{i,1}+\cdots+ k_{d,N}u_{i,d})\nonumber\\ &\quad+\sum_{i=s_0+1}^{s}(\widetilde{p}_{i,N}(h))(k_{1,N}u_{i,1}+\cdots+ k_{d,N}u_{i,d})\bigg) \bigg\rVert_{C^{\infty}[L(N)]}\leq M. \end{align} $$
Since there are only finitely many choices for the numbers
![]() $k_{1, N},\ldots ,k_{d, N}$
, we have that if our claim fails, there are
$k_{1, N},\ldots ,k_{d, N}$
, we have that if our claim fails, there are
![]() $k_1,\ldots ,k_d\in \mathbb {Z}$
, so that the inequality
$k_1,\ldots ,k_d\in \mathbb {Z}$
, so that the inequality
 $$ \begin{align} &\bigg\lVert e\bigg(\sum_{i=1}^{s_0}(q_{i,N}(h)+p_{i,N}(h))(k_{1}u_{i,1}+\cdots+ k_{d}u_{i,d})\nonumber\\ &\quad+\sum_{i=s_0+1}^{s}(\widetilde{p}_{i,N}(h))(k_{1}u_{i,1}+\cdots+ k_{d}u_{i,d})\bigg) \bigg\rVert_{C^{\infty}[L(N)]}\leq M \end{align} $$
$$ \begin{align} &\bigg\lVert e\bigg(\sum_{i=1}^{s_0}(q_{i,N}(h)+p_{i,N}(h))(k_{1}u_{i,1}+\cdots+ k_{d}u_{i,d})\nonumber\\ &\quad+\sum_{i=s_0+1}^{s}(\widetilde{p}_{i,N}(h))(k_{1}u_{i,1}+\cdots+ k_{d}u_{i,d})\bigg) \bigg\rVert_{C^{\infty}[L(N)]}\leq M \end{align} $$
holds for infinitely many
![]() $N\in \mathbb {N}$
. We will also denote the horizontal character corresponding to the d-tuplet
$N\in \mathbb {N}$
. We will also denote the horizontal character corresponding to the d-tuplet
![]() $(k_1,\ldots ,k_d)$
by
$(k_1,\ldots ,k_d)$
by
![]() $\chi $
. Thus, we have eliminated the dependence of the character
$\chi $
. Thus, we have eliminated the dependence of the character
![]() $\chi $
on N.
$\chi $
on N.
Denote
![]() $\widetilde {u_i}=k_1u_{i,1}+\cdots + k_du_{i,d}$
. We will show that the above hypotheses imply that all the numbers
$\widetilde {u_i}=k_1u_{i,1}+\cdots + k_du_{i,d}$
. We will show that the above hypotheses imply that all the numbers
![]() $\widetilde {u_i}$
equal
$\widetilde {u_i}$
equal
![]() $0$
. Thus, suppose that this is not valid and we will reach a contradiction. We consider two cases.
$0$
. Thus, suppose that this is not valid and we will reach a contradiction. We consider two cases.
Case 1. First, suppose that all of the numbers
![]() $\widetilde {u_i}$
with
$\widetilde {u_i}$
with
![]() $1\leq i\leq s_0$
are zero, which implies that the first summand in equation (33) vanishes. Naturally, equation (33) is simplified to
$1\leq i\leq s_0$
are zero, which implies that the first summand in equation (33) vanishes. Naturally, equation (33) is simplified to
 $$ \begin{align} \bigg\lVert e\bigg(\sum_{i=s_0+1}^{s}\widetilde{p}_{i,N}(h)\widetilde{u_i}\bigg) \bigg\rVert_{C^{\infty}[L(N)]}\leq M. \end{align} $$
$$ \begin{align} \bigg\lVert e\bigg(\sum_{i=s_0+1}^{s}\widetilde{p}_{i,N}(h)\widetilde{u_i}\bigg) \bigg\rVert_{C^{\infty}[L(N)]}\leq M. \end{align} $$
We recall here that we had defined
![]() $\widetilde {p}_{i,N}(h)=\widetilde {p}_i(N+h)$
. Let
$\widetilde {p}_{i,N}(h)=\widetilde {p}_i(N+h)$
. Let
![]() $Q(t)= \sum _{i=s_0+1}^{s}\widetilde {u_i}\widetilde {p}_{i}(t)$
. This is a linear combination of the polynomials
$Q(t)= \sum _{i=s_0+1}^{s}\widetilde {u_i}\widetilde {p}_{i}(t)$
. This is a linear combination of the polynomials
![]() $\widetilde {p}_i(t)$
. However, this linear combination is not a polynomial in
$\widetilde {p}_i(t)$
. However, this linear combination is not a polynomial in
![]() $\mathbb {Q}[t]$
due to our assumptions on the polynomials
$\mathbb {Q}[t]$
due to our assumptions on the polynomials
![]() $\widetilde {p}_i(n)$
, unless, of course, all the coefficients
$\widetilde {p}_i(n)$
, unless, of course, all the coefficients
![]() $\widetilde {u_i}$
(for
$\widetilde {u_i}$
(for
![]() $s_0+1\leq i\leq s$
) in this combination are zero, which we have supposed to not be the case. Thus,
$s_0+1\leq i\leq s$
) in this combination are zero, which we have supposed to not be the case. Thus,
![]() $Q(t)$
has at least one irrational coefficient (except the constant term) and is equidistributed on
$Q(t)$
has at least one irrational coefficient (except the constant term) and is equidistributed on
![]() $\mathbb {T}$
. The relation in equation (34) implies that
$\mathbb {T}$
. The relation in equation (34) implies that
![]() $\lVert e(Q(N+h)) \rVert _{C^{\infty }[L(N)]}\leq M$
for infinitely many N. It is not difficult to see by calculating the coefficients in
$\lVert e(Q(N+h)) \rVert _{C^{\infty }[L(N)]}\leq M$
for infinitely many N. It is not difficult to see by calculating the coefficients in
![]() $Q(N+h)$
that this fails for N large enough.
$Q(N+h)$
that this fails for N large enough.
Case 2. Suppose now that at least one of the numbers
![]() $\widetilde {u_i}$
with
$\widetilde {u_i}$
with
![]() $1\leq i\leq s_0$
is non-zero. Furthermore, assume l is a positive integer that is larger than the degrees of the polynomials
$1\leq i\leq s_0$
is non-zero. Furthermore, assume l is a positive integer that is larger than the degrees of the polynomials
![]() $p_{i, N}(h),\widetilde {p}_{j, N}(h)$
(for all admissible values of the indices
$p_{i, N}(h),\widetilde {p}_{j, N}(h)$
(for all admissible values of the indices
![]() $i, j$
) as well as the degrees of the functions
$i, j$
) as well as the degrees of the functions
![]() $x_i$
, but l is also smaller than all the numbers
$x_i$
, but l is also smaller than all the numbers
![]() $k_i$
. Recall that we have picked
$k_i$
. Recall that we have picked
![]() $k_i$
to be very large in relation to the degrees of the polynomials
$k_i$
to be very large in relation to the degrees of the polynomials
![]() $p_{i},\widetilde {p}_{j}$
and degrees of the functions
$p_{i},\widetilde {p}_{j}$
and degrees of the functions
![]() $x_i$
in the beginning, thus we can find ‘many’ such numbers l. The fact that l is larger than the degrees of the functions
$x_i$
in the beginning, thus we can find ‘many’ such numbers l. The fact that l is larger than the degrees of the functions
![]() $x_i$
combined with Proposition A.1 implies that
$x_i$
combined with Proposition A.1 implies that
![]() $x_i^{(l)}(t)\to 0$
, as
$x_i^{(l)}(t)\to 0$
, as
![]() $t\to +\infty $
.
$t\to +\infty $
.
For a number l as above, the coefficient of the term
![]() $h^{l}$
in the polynomial appearing in equation (33) is equal to
$h^{l}$
in the polynomial appearing in equation (33) is equal to
 $$ \begin{align*} \frac{1}{l!}\sum_{i=1}^{s_0}x_i^{(l)}(N) \widetilde{u_i} \end{align*} $$
$$ \begin{align*} \frac{1}{l!}\sum_{i=1}^{s_0}x_i^{(l)}(N) \widetilde{u_i} \end{align*} $$
and, thus, it does not depend on the polynomials
![]() $p_i,\widetilde {p}_j$
. Using the definition of the smoothness norms, equation (33) implies that
$p_i,\widetilde {p}_j$
. Using the definition of the smoothness norms, equation (33) implies that
 $$ \begin{align*} L(N)^{l}\bigg\lVert \frac{1}{l!}\sum_{i=1}^{s_0}x_i^{(l)}(N) \widetilde{u_i} \bigg\rVert_{\mathbb{T}}\leq M \end{align*} $$
$$ \begin{align*} L(N)^{l}\bigg\lVert \frac{1}{l!}\sum_{i=1}^{s_0}x_i^{(l)}(N) \widetilde{u_i} \bigg\rVert_{\mathbb{T}}\leq M \end{align*} $$
for infinitely many
![]() $N\in \mathbb {N}$
. The last inequality becomes
$N\in \mathbb {N}$
. The last inequality becomes
 $$ \begin{align*} L(N)^{l}\bigg|\sum_{i=1}^{s_0}x_i^{(l)}(N)\widetilde{u_i}\bigg|\leq l!M \end{align*} $$
$$ \begin{align*} L(N)^{l}\bigg|\sum_{i=1}^{s_0}x_i^{(l)}(N)\widetilde{u_i}\bigg|\leq l!M \end{align*} $$
for large enough N, because all functions
![]() $x_i^{l}(t)$
go to 0. However, the Hardy field function inside the absolute value above has the same growth rate as the function
$x_i^{l}(t)$
go to 0. However, the Hardy field function inside the absolute value above has the same growth rate as the function
![]() $x_1^{(l)}(t)$
, since the functions
$x_1^{(l)}(t)$
, since the functions
![]() $x_1,\ldots ,x_{s_0}$
are strongly non-polynomial and have distinct growth rates (recall that
$x_1,\ldots ,x_{s_0}$
are strongly non-polynomial and have distinct growth rates (recall that
![]() $x_1$
has the largest growth rate among the
$x_1$
has the largest growth rate among the
![]() $x_i$
), unless, of course,
$x_i$
), unless, of course,
![]() $\widetilde {u}_1=0$
. If the latter does not hold, we get
$\widetilde {u}_1=0$
. If the latter does not hold, we get
 $$ \begin{align*} \bigg|x_1^{(l)}(N)\widetilde{u}_1 \bigg|\leq \frac{C}{L(N)^l} \end{align*} $$
$$ \begin{align*} \bigg|x_1^{(l)}(N)\widetilde{u}_1 \bigg|\leq \frac{C}{L(N)^l} \end{align*} $$
for infinitely many N and some constant C, which contradicts equation (26). Thus, we eventually deduce that
![]() $\widetilde {u}_1=k_1u_{1,1}+\cdots + k_du_{1,d}=0$
. Repeating the same argument, we get inductively that
$\widetilde {u}_1=k_1u_{1,1}+\cdots + k_du_{1,d}=0$
. Repeating the same argument, we get inductively that
![]() $\widetilde {u}_i=k_1u_{i,1}+\cdots + k_du_{i,d}$
=0 for all
$\widetilde {u}_i=k_1u_{i,1}+\cdots + k_du_{i,d}$
=0 for all
![]() $1\leq i\leq s_0$
, which is a contradiction.
$1\leq i\leq s_0$
, which is a contradiction.
To summarize, we have shown that if the sequence in equation (30) is not
![]() $\delta $
-equidistributed for all large enough N, then all the numbers
$\delta $
-equidistributed for all large enough N, then all the numbers
![]() $\widetilde {u}_i=k_1u_{i,1}+\cdots + k_du_{i,d}$
are zero. Equivalently, we have
$\widetilde {u}_i=k_1u_{i,1}+\cdots + k_du_{i,d}$
are zero. Equivalently, we have
![]() $\chi \circ \pi (u_i)=0$
for all
$\chi \circ \pi (u_i)=0$
for all
![]() $1\leq i\leq s$
. This implies that the character
$1\leq i\leq s$
. This implies that the character
![]() $\chi $
is the trivial character on
$\chi $
is the trivial character on
![]() $X'$
. Indeed, the character
$X'$
. Indeed, the character
![]() $\chi $
annihilates all elements
$\chi $
annihilates all elements
![]() $u_1^{n_1}\cdots u_s^{n_s}\Gamma $
, where
$u_1^{n_1}\cdots u_s^{n_s}\Gamma $
, where
![]() $n_1,\ldots ,n_s\in \mathbb {Z}$
and by density of those elements on
$n_1,\ldots ,n_s\in \mathbb {Z}$
and by density of those elements on
![]() $X'$
(recall our assumption that
$X'$
(recall our assumption that
![]() $X'$
is also equal to the nilmanifold
$X'$
is also equal to the nilmanifold
![]() $\overline {u_1^{\mathbb {Z}}\cdots u_s^{\mathbb {Z}}\Gamma }$
),
$\overline {u_1^{\mathbb {Z}}\cdots u_s^{\mathbb {Z}}\Gamma }$
),
![]() $\chi $
is zero everywhere. This is a contradiction (the horizontal characters appearing when we applied Theorem F are assumed to be non-trivial).
$\chi $
is zero everywhere. This is a contradiction (the horizontal characters appearing when we applied Theorem F are assumed to be non-trivial).
In conclusion, we have that the finite polynomial sequence in equation (30) is
![]() $\delta $
-equidistributed for N sufficiently large. Thus, we conclude that the averages in equation (25) are
$\delta $
-equidistributed for N sufficiently large. Thus, we conclude that the averages in equation (25) are
![]() $\delta \lVert F(w_N \cdot ) \rVert _{\text {Lip}(X')}=\delta \lVert F \rVert _{\text {Lip}(X')}$
close to the quantity
$\delta \lVert F(w_N \cdot ) \rVert _{\text {Lip}(X')}=\delta \lVert F \rVert _{\text {Lip}(X')}$
close to the quantity
![]() $ \int _{X'} F(w_N x)\ dm_{X'}(x)$
. The action of
$ \int _{X'} F(w_N x)\ dm_{X'}(x)$
. The action of
![]() $w_N$
on
$w_N$
on
![]() $X'$
preserves the Haar measure of
$X'$
preserves the Haar measure of
![]() $X'$
, so we get that the last integral is equal to
$X'$
, so we get that the last integral is equal to
![]() $\int _{X'} F(x) \ dm_{X'}(x)$
. Taking
$\int _{X'} F(x) \ dm_{X'}(x)$
. Taking
![]() $\delta \to 0$
, we finish the proof.
$\delta \to 0$
, we finish the proof.
Proof of Theorem 1.1
As we explained in the previous section (before the statement of Lemma 3.2), the first part follows from the second part (see also [Reference Frantzikinakis4, Lemma 5.1]) and, in turn, this second part follows using similar arguments as in the proof of Theorem 1.2. We only highlight the main differences here. All the disparities appear in the part where we reduce Proposition 4.1 to Lemma 4.2.
(a) In equation (22), all the functions
![]() $f_1,\ldots ,f_s$
satisfy equation (8) (there are no functions among the
$f_1,\ldots ,f_s$
satisfy equation (8) (there are no functions among the
![]() $f_i$
that satisfy
$f_i$
that satisfy
![]() $\lim \nolimits _{t\to +\infty }|f_i(t)|<\infty $
). We also have
$\lim \nolimits _{t\to +\infty }|f_i(t)|<\infty $
). We also have
![]() $k=s$
.
$k=s$
.
(b) We do not have to make the reduction to the case where the polynomials
![]() $\widetilde {p}_1,\ldots ,\widetilde {p}_{\ell }$
are linearly independent. There cannot be a non-trivial linear combination of them that is zero, because that would violate equation (8).
$\widetilde {p}_1,\ldots ,\widetilde {p}_{\ell }$
are linearly independent. There cannot be a non-trivial linear combination of them that is zero, because that would violate equation (8).
(c) The limit of the averages is again
![]() $\int _{X'} F(x) \ dm_{X'}(x)$
, where
$\int _{X'} F(x) \ dm_{X'}(x)$
, where
![]() $X'=\overline {u_1^{\mathbb {R}}\cdots u_s^{\mathbb {R}}\Gamma }$
by Lemma 4.2. We would like to show that the limit is equal to
$X'=\overline {u_1^{\mathbb {R}}\cdots u_s^{\mathbb {R}}\Gamma }$
by Lemma 4.2. We would like to show that the limit is equal to
![]() $\int _{X"} Fdm_X"$
, where
$\int _{X"} Fdm_X"$
, where
![]() $X"$
is the nilmanifold
$X"$
is the nilmanifold
![]() $\overline {b_1^{\mathbb {R}}\cdots b_k^{\mathbb {R}}\Gamma }$
. Recall that each
$\overline {b_1^{\mathbb {R}}\cdots b_k^{\mathbb {R}}\Gamma }$
. Recall that each
![]() $u_i$
is equal to
$u_i$
is equal to
![]() $b_1^{c_{i,1}}\cdots b_k^{c_{i,k}}$
(by equation (21)) and the numbers
$b_1^{c_{i,1}}\cdots b_k^{c_{i,k}}$
(by equation (21)) and the numbers
![]() $c_{i,j}$
form an invertible
$c_{i,j}$
form an invertible
![]() $k\times k$
matrix (due to the linear independence assumption on the original functions
$k\times k$
matrix (due to the linear independence assumption on the original functions
![]() $a_1,\ldots ,a_k$
). Thus, we can also write
$a_1,\ldots ,a_k$
). Thus, we can also write
![]() $b_i=\prod _{j=1}^{k}u_i^{c^{\prime }_{i,j}}$
for some numbers
$b_i=\prod _{j=1}^{k}u_i^{c^{\prime }_{i,j}}$
for some numbers
![]() $c^{\prime }_{i,j}$
(here, we also use that the elements
$c^{\prime }_{i,j}$
(here, we also use that the elements
![]() $b_i$
are pairwise commuting). Combining the above, we have that
$b_i$
are pairwise commuting). Combining the above, we have that
![]() $b_1^{\mathbb {R}}\cdots b_k^{\mathbb {R}}=u_1^{\mathbb {R}}\cdots u_k^{\mathbb {R}}$
and thus the closures of their projections on
$b_1^{\mathbb {R}}\cdots b_k^{\mathbb {R}}=u_1^{\mathbb {R}}\cdots u_k^{\mathbb {R}}$
and thus the closures of their projections on
![]() $G/\Gamma $
define the same subnilmanifold.
$G/\Gamma $
define the same subnilmanifold.
4.1 Proof of Theorem 1.3
Finally, we provide a proof of Theorem 1.3. We use the following proposition from [Reference Tsinas18]. Although it will not be used in the proof, we have to assume below that the Hardy field
![]() $\mathcal {H}$
that we work with is closed under composition and compositional inversion of functions, since the following proposition was proven under this assumption.
$\mathcal {H}$
that we work with is closed under composition and compositional inversion of functions, since the following proposition was proven under this assumption.
Proposition 4.3. [Reference Tsinas18, Proposition 3.1]
Let
![]() $\mathcal {H}$
be a Hardy field that contains the field
$\mathcal {H}$
be a Hardy field that contains the field
![]() $\mathcal {LE}$
of logarithmico-exponential functions and is closed under composition and compositional inversion of functions (when defined). Assume that the functions
$\mathcal {LE}$
of logarithmico-exponential functions and is closed under composition and compositional inversion of functions (when defined). Assume that the functions
![]() $a_1,\ldots ,a_k\in \mathcal {H}$
have polynomial growth and suppose that the following two conditions hold:
$a_1,\ldots ,a_k\in \mathcal {H}$
have polynomial growth and suppose that the following two conditions hold:
-
(i) the functions
 $a_1,\ldots ,a_k$
dominate the logarithmic function
$a_1,\ldots ,a_k$
dominate the logarithmic function
 $\log t$
;
$\log t$
; -
(ii) the pairwise differences
 $a_i-a_j$
dominate the logarithmic function
$a_i-a_j$
dominate the logarithmic function
 $\log t$
for any
$\log t$
for any
 $i\neq j$
.
$i\neq j$
.
Then, there exists a positive integer s, such that for any measure-preserving system
![]() $(X,\mu ,T)$
, functions
$(X,\mu ,T)$
, functions
![]() $f_1\in L^{\infty }(\mu )$
and
$f_1\in L^{\infty }(\mu )$
and
![]() $f_{2,N},\ldots ,f_{k,N}\in L^{\infty }(\mu )$
, all bounded by
$f_{2,N},\ldots ,f_{k,N}\in L^{\infty }(\mu )$
, all bounded by
![]() $1$
, with
$1$
, with
![]() $f_1\perp Z_{s}(X)$
, the expression
$f_1\perp Z_{s}(X)$
, the expression
converges to 0, as
![]() $N\to +\infty $
.
$N\to +\infty $
.
Proof of Theorem 1.3
Using a standard ergodic decomposition argument, we may assume that the system
![]() $(X,\mu , T)$
is ergodic. We can also rescale the functions
$(X,\mu , T)$
is ergodic. We can also rescale the functions
![]() $f_i\in L^{\infty }(\mu )$
so that they are 1-bounded. Our first objective is to apply Proposition 4.3 to reduce the problem to the case where the system X is a nilsystem. If the functions
$f_i\in L^{\infty }(\mu )$
so that they are 1-bounded. Our first objective is to apply Proposition 4.3 to reduce the problem to the case where the system X is a nilsystem. If the functions
![]() $a_1,\ldots ,a_k$
are such that the conditions of Proposition 4.3 are satisfied, then this can be done instantly. If this does not hold, we have to perform a series of reductions to be able to apply Proposition 4.3. We do this in two steps.
$a_1,\ldots ,a_k$
are such that the conditions of Proposition 4.3 are satisfied, then this can be done instantly. If this does not hold, we have to perform a series of reductions to be able to apply Proposition 4.3. We do this in two steps.
(a) First, assume there exists one function among the
![]() $a_i$
(say
$a_i$
(say
![]() $a_1$
for simplicity), which has growth rate smaller than or equal to
$a_1$
for simplicity), which has growth rate smaller than or equal to
![]() $\log t$
. Then, using equations (8) and (9), we deduce that
$\log t$
. Then, using equations (8) and (9), we deduce that
![]() $a_1$
converges monotonically to some real number c and the integer part of
$a_1$
converges monotonically to some real number c and the integer part of
![]() $a_1(n)$
becomes a constant. Thus, the asymptotic behaviour of the averages in equation (10) is the same if we substitute the term
$a_1(n)$
becomes a constant. Thus, the asymptotic behaviour of the averages in equation (10) is the same if we substitute the term
![]() $T^{ \left \lfloor {a_1(n)} \right \rfloor f_1}$
with the term
$T^{ \left \lfloor {a_1(n)} \right \rfloor f_1}$
with the term
![]() $T^{ \left \lfloor {c} \right \rfloor }f_1$
. Consequently, we only need to show that the averages
$T^{ \left \lfloor {c} \right \rfloor }f_1$
. Consequently, we only need to show that the averages
converge in norm. Repeating the same argument, we eliminate all functions
![]() $a_i$
that grow slower than
$a_i$
that grow slower than
![]() $\log t$
.
$\log t$
.
(b) Due to the reduction in the previous step, we have a sub-collection of the original functions, so that all functions in this new set dominate
![]() $\log t$
. We will denote this collection by
$\log t$
. We will denote this collection by
![]() $a_1,\ldots ,a_k$
again, and our task is to show that the averages
$a_1,\ldots ,a_k$
again, and our task is to show that the averages
converge in mean (for all systems). Our next objective is to eliminate pairs of functions, whose difference grows slower than
![]() $\log t$
so that we can ultimately apply Proposition 4.3.
$\log t$
so that we can ultimately apply Proposition 4.3.
Assume that two of the functions (say
![]() $a_1,a_2$
) are such that their difference is dominated by
$a_1,a_2$
) are such that their difference is dominated by
![]() $\log t$
. We observe that the function
$\log t$
. We observe that the function
![]() $a_1(t)$
goes to
$a_1(t)$
goes to
![]() $\pm \infty $
as
$\pm \infty $
as
![]() $t\to +\infty $
, since it dominates
$t\to +\infty $
, since it dominates
![]() $\log t$
. In that case, the function
$\log t$
. In that case, the function
![]() $a_1(t)$
satisfies equation (8) and by Theorem A, the sequence
$a_1(t)$
satisfies equation (8) and by Theorem A, the sequence
![]() $a_1(n)$
is equidistributed
$a_1(n)$
is equidistributed
![]() $(mod\ 1)$
. Observe that since
$(mod\ 1)$
. Observe that since
![]() $a_1-a_2$
must satisfy equation (9), we must have
$a_1-a_2$
must satisfy equation (9), we must have
![]() $a_2(t)=a_1(t)+c+x(t)$
, where the function
$a_2(t)=a_1(t)+c+x(t)$
, where the function
![]() $x(t)\in \mathcal {H}$
converges to
$x(t)\in \mathcal {H}$
converges to
![]() $0$
monotonically and c is a real number. Thus, for
$0$
monotonically and c is a real number. Thus, for
![]() $t\in \mathbb {R}$
sufficiently large, we have
$t\in \mathbb {R}$
sufficiently large, we have
where
![]() $\varepsilon (t)\in \{0,\pm 1,\pm 2\}$
and the value of
$\varepsilon (t)\in \{0,\pm 1,\pm 2\}$
and the value of
![]() $\varepsilon (t)$
depends on whether the inequalities
$\varepsilon (t)$
depends on whether the inequalities
and
hold or not, as well as whether
![]() $x(t)$
is eventually positive or negative.
$x(t)$
is eventually positive or negative.
Define
![]() $A_z=\{t\in \mathbb {R}, \varepsilon (t)=z\}$
for
$A_z=\{t\in \mathbb {R}, \varepsilon (t)=z\}$
for
![]() $z\in \{0,\pm 1,\pm 2\}$
. Then, we see that our multiple averages are equal to the sum
$z\in \{0,\pm 1,\pm 2\}$
. Then, we see that our multiple averages are equal to the sum
For a fixed z, we want to show that the corresponding average converges. For
![]() $n\in \mathbb {N}$
large enough, we will approximate the sequence
$n\in \mathbb {N}$
large enough, we will approximate the sequence
![]() ${\mathbf 1}_{A_z}(n)$
by sequences of the form
${\mathbf 1}_{A_z}(n)$
by sequences of the form
![]() $F(\{a_1(n)\})$
, where F is a continuous function.
$F(\{a_1(n)\})$
, where F is a continuous function.
We establish this for
![]() $z=0$
(the other cases follow similarly). Assume that
$z=0$
(the other cases follow similarly). Assume that
![]() $x(t)$
decreases to 0 (the other case) is similar, which means that
$x(t)$
decreases to 0 (the other case) is similar, which means that
![]() $x(t)$
is eventually positive and also
$x(t)$
is eventually positive and also
![]() $\{x(t)\}=x(t)$
for t sufficiently large. In addition, we can also assume that c is positive. Observe that for
$\{x(t)\}=x(t)$
for t sufficiently large. In addition, we can also assume that c is positive. Observe that for
![]() $t\in A_{0}$
, we have
$t\in A_{0}$
, we have
by the definition of
![]() $A_0$
. This is equivalent to the inequalities
$A_0$
. This is equivalent to the inequalities
 $$ \begin{align*} &\{a_1(t)+c\}+\{x(t)\}\leq 1,\\ &\{a_1(t)\}+\{c\}\leq 1, \end{align*} $$
$$ \begin{align*} &\{a_1(t)+c\}+\{x(t)\}\leq 1,\\ &\{a_1(t)\}+\{c\}\leq 1, \end{align*} $$
which can be condensed into
since we assumed for simplicity that
![]() $x(t)$
is eventually positive. To summarize, we have shown that
$x(t)$
is eventually positive. To summarize, we have shown that
Let
![]() $\varepsilon>0$
be a small number. Since we have that the function
$\varepsilon>0$
be a small number. Since we have that the function
![]() $x(t)$
decreases to
$x(t)$
decreases to
![]() $ 0$
, we have that
$ 0$
, we have that
![]() $\{x(t)\}<\varepsilon $
for t large enough. Consider the set
$\{x(t)\}<\varepsilon $
for t large enough. Consider the set
Then, for sufficiently large values of n, we observe that if
![]() $n\in A_{\varepsilon }$
, then the inequality
$n\in A_{\varepsilon }$
, then the inequality
holds as well. Namely,
![]() $A_\varepsilon \subseteq A_0$
. Let us denote
$A_\varepsilon \subseteq A_0$
. Let us denote
![]() $B_{\varepsilon }=[0,1-{c}-\varepsilon ]$
for convenience and observe that
$B_{\varepsilon }=[0,1-{c}-\varepsilon ]$
for convenience and observe that
Now we approximate the function
![]() $\mathbf {1}_{B_\varepsilon }$
by a continuous function in the uniform norm, where
$\mathbf {1}_{B_\varepsilon }$
by a continuous function in the uniform norm, where
![]() $\mathbf {1}_{B_{\varepsilon }}$
is considered a function on the torus
$\mathbf {1}_{B_{\varepsilon }}$
is considered a function on the torus
![]() $\mathbb {T}$
in the natural way. We can define a continuous function on
$\mathbb {T}$
in the natural way. We can define a continuous function on
![]() $\mathbb {T}$
, such that
$\mathbb {T}$
, such that
![]() $F_{\varepsilon }$
agrees with
$F_{\varepsilon }$
agrees with
![]() $\mathbf {1}_{B_\varepsilon }$
on the set
$\mathbf {1}_{B_\varepsilon }$
on the set
and such that
![]() $\lVert F_{\varepsilon }-\mathbf {1}_{B_\varepsilon } \rVert _{\infty }\leq 2 $
. (In the case that c is an integer, we make natural modifications to this set. For example, one could define the function
$\lVert F_{\varepsilon }-\mathbf {1}_{B_\varepsilon } \rVert _{\infty }\leq 2 $
. (In the case that c is an integer, we make natural modifications to this set. For example, one could define the function
![]() $F_{\varepsilon }$
so that it agrees with
$F_{\varepsilon }$
so that it agrees with
![]() $\mathbf {1}_{\mathcal {B}_{\varepsilon }}$
on
$\mathbf {1}_{\mathcal {B}_{\varepsilon }}$
on
![]() $[\varepsilon ,1-2\varepsilon ]$
. Basically, we only require the function
$[\varepsilon ,1-2\varepsilon ]$
. Basically, we only require the function
![]() $F_{\varepsilon }$
to agree with
$F_{\varepsilon }$
to agree with
![]() $\mathbf {1}_{B_{\varepsilon }}$
on a set of measure
$\mathbf {1}_{B_{\varepsilon }}$
on a set of measure
![]() $1-O(\varepsilon )$
for our argument to work.) We suppose that
$1-O(\varepsilon )$
for our argument to work.) We suppose that
![]() $\varepsilon $
is small enough so that these intervals are well defined. Observe that
$\varepsilon $
is small enough so that these intervals are well defined. Observe that
![]() $\mathbf {1}_{B_{\varepsilon }}$
is equal to 1 on the first interval of this union and equal to 0 on the second interval.
$\mathbf {1}_{B_{\varepsilon }}$
is equal to 1 on the first interval of this union and equal to 0 on the second interval.
Observe that
 $$ \begin{align*} A_0\setminus A_{\varepsilon}&=\{n\in \mathbb{N}\colon 1-\{c\}-\varepsilon < \{a_1(n)\} \leq 1-\{c\}-\{x(n)\} \}\\&\subseteq \{n\in \mathbb{N}\colon \{a_1(n)\}\in [1-\{c\}-\varepsilon,1-\{c\} ] \}. \end{align*} $$
$$ \begin{align*} A_0\setminus A_{\varepsilon}&=\{n\in \mathbb{N}\colon 1-\{c\}-\varepsilon < \{a_1(n)\} \leq 1-\{c\}-\{x(n)\} \}\\&\subseteq \{n\in \mathbb{N}\colon \{a_1(n)\}\in [1-\{c\}-\varepsilon,1-\{c\} ] \}. \end{align*} $$
Since the function
![]() $a_1(t)$
is equidistributed modulo 1, we conclude that the set
$a_1(t)$
is equidistributed modulo 1, we conclude that the set
![]() $A_0\setminus A_{\varepsilon }$
has upper density at most
$A_0\setminus A_{\varepsilon }$
has upper density at most
![]() $\varepsilon $
. Therefore, we have
$\varepsilon $
. Therefore, we have
 $$ \begin{align} &\big\lVert \underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} {\mathbf 1}_{A_0}(n)\ T^{ \left\lfloor {a_1(n)} \right\rfloor }(f_1\cdot T^{ \left\lfloor {c} \right\rfloor }f_2)\cdot T^{ \left\lfloor {a_3(n)} \right\rfloor }f_3\cdots T^{ \left\lfloor {a_k(n)} \right\rfloor } f_k \nonumber\\ &\qquad-\underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} \mathbf{1}_{B_{\varepsilon}}(\{a_1(n)\})\ T^{ \left\lfloor {a_1(n)} \right\rfloor }(f_1\cdot T^{ \left\lfloor {c} \right\rfloor }f_2)\cdot T^{ \left\lfloor {a_3(n)} \right\rfloor }f_3\cdots T^{ \left\lfloor {a_k(n)} \right\rfloor } f_k \big\rVert_{L^2(\mu)} \nonumber\\ &\quad\leq\operatorname*{\mathrm{\mathbb{E}}}_{1\leq n\leq N} \mathbf{1}_{A_0\setminus A_{\varepsilon}}(n)\lVert \mathbf{1}_{A_{\varepsilon}}-1_{A_{\varepsilon}\setminus A_0} \rVert_{\infty} \leq 2\varepsilon+o_N(1), \end{align} $$
$$ \begin{align} &\big\lVert \underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} {\mathbf 1}_{A_0}(n)\ T^{ \left\lfloor {a_1(n)} \right\rfloor }(f_1\cdot T^{ \left\lfloor {c} \right\rfloor }f_2)\cdot T^{ \left\lfloor {a_3(n)} \right\rfloor }f_3\cdots T^{ \left\lfloor {a_k(n)} \right\rfloor } f_k \nonumber\\ &\qquad-\underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} \mathbf{1}_{B_{\varepsilon}}(\{a_1(n)\})\ T^{ \left\lfloor {a_1(n)} \right\rfloor }(f_1\cdot T^{ \left\lfloor {c} \right\rfloor }f_2)\cdot T^{ \left\lfloor {a_3(n)} \right\rfloor }f_3\cdots T^{ \left\lfloor {a_k(n)} \right\rfloor } f_k \big\rVert_{L^2(\mu)} \nonumber\\ &\quad\leq\operatorname*{\mathrm{\mathbb{E}}}_{1\leq n\leq N} \mathbf{1}_{A_0\setminus A_{\varepsilon}}(n)\lVert \mathbf{1}_{A_{\varepsilon}}-1_{A_{\varepsilon}\setminus A_0} \rVert_{\infty} \leq 2\varepsilon+o_N(1), \end{align} $$
where we used the fact that
![]() $ \mathbf {1}_{A_{\varepsilon }}(n)=\mathbf {1}_{B_\varepsilon }(\{a_1(n)\})$
for all
$ \mathbf {1}_{A_{\varepsilon }}(n)=\mathbf {1}_{B_\varepsilon }(\{a_1(n)\})$
for all
![]() $n\in \mathbb {N}$
, the trivial bound for the values of
$n\in \mathbb {N}$
, the trivial bound for the values of
![]() $n\in A_{0}\setminus A_{\varepsilon }$
and the fact that the set
$n\in A_{0}\setminus A_{\varepsilon }$
and the fact that the set
![]() $A_{0}\setminus A_{\varepsilon }$
has upper density at most
$A_{0}\setminus A_{\varepsilon }$
has upper density at most
![]() $\varepsilon $
.
$\varepsilon $
.
We do a similar comparison for the averages weighted by
![]() $F_{\varepsilon }(\{a_1(n)\})$
and
$F_{\varepsilon }(\{a_1(n)\})$
and
![]() $1_{B_{\varepsilon }}(\{a_1(n)\})$
. To be more specific, we reiterate that the functions
$1_{B_{\varepsilon }}(\{a_1(n)\})$
. To be more specific, we reiterate that the functions
![]() $1_{B_{\varepsilon }}$
and
$1_{B_{\varepsilon }}$
and
![]() $F_{\varepsilon }$
agree on the set
$F_{\varepsilon }$
agree on the set
Accordingly, we have
![]() $\mathbf {1}_{B_{\varepsilon }}(\{a_1(n)\})=F_{\varepsilon }(\{a_1(n)\})$
, unless
$\mathbf {1}_{B_{\varepsilon }}(\{a_1(n)\})=F_{\varepsilon }(\{a_1(n)\})$
, unless
Let
![]() $C_{\varepsilon }$
denote the set of
$C_{\varepsilon }$
denote the set of
![]() $n\in \mathbb {N}$
for which
$n\in \mathbb {N}$
for which
![]() $\{a_1(n)\}$
belongs to this union. This union has measure
$\{a_1(n)\}$
belongs to this union. This union has measure
![]() $4\varepsilon $
, which implies that the upper density of
$4\varepsilon $
, which implies that the upper density of
![]() $C_{\varepsilon }$
is at most
$C_{\varepsilon }$
is at most
![]() $4\varepsilon $
(since
$4\varepsilon $
(since
![]() $a_1(n)$
is equidistributed modulo 1). Hence, we infer that
$a_1(n)$
is equidistributed modulo 1). Hence, we infer that
 $$ \begin{align} &\big\lVert \underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} F_{\varepsilon}(\{a_1(n)\})\ T^{ \left\lfloor {a_1(n)} \right\rfloor }(f_1\cdot T^{ \left\lfloor {c} \right\rfloor }f_2)\cdot T^{ \left\lfloor {a_3(n)} \right\rfloor }f_3\cdots T^{ \left\lfloor {a_k(n)} \right\rfloor } f_k\nonumber\\ &\qquad-\underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} \mathbf{1}_{B_{\varepsilon}}(\{a_1(n)\})\ T^{ \left\lfloor {a_1(n)} \right\rfloor }(f_1\cdot T^{ \left\lfloor {c} \right\rfloor }f_2)\cdot T^{ \left\lfloor {a_3(n)} \right\rfloor }f_3\cdots T^{ \left\lfloor {a_k(n)} \right\rfloor } f_k \big\rVert_{L^2(\mu)}\nonumber\\ &\quad\leq\operatorname*{\mathrm{\mathbb{E}}}_{1\leq n\leq N} 1_{C_{\varepsilon}}(n)\lVert F_{\varepsilon}-1_{B_{\varepsilon}} \rVert_{\infty} \leq 8\varepsilon +o_N(1), \end{align} $$
$$ \begin{align} &\big\lVert \underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} F_{\varepsilon}(\{a_1(n)\})\ T^{ \left\lfloor {a_1(n)} \right\rfloor }(f_1\cdot T^{ \left\lfloor {c} \right\rfloor }f_2)\cdot T^{ \left\lfloor {a_3(n)} \right\rfloor }f_3\cdots T^{ \left\lfloor {a_k(n)} \right\rfloor } f_k\nonumber\\ &\qquad-\underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} \mathbf{1}_{B_{\varepsilon}}(\{a_1(n)\})\ T^{ \left\lfloor {a_1(n)} \right\rfloor }(f_1\cdot T^{ \left\lfloor {c} \right\rfloor }f_2)\cdot T^{ \left\lfloor {a_3(n)} \right\rfloor }f_3\cdots T^{ \left\lfloor {a_k(n)} \right\rfloor } f_k \big\rVert_{L^2(\mu)}\nonumber\\ &\quad\leq\operatorname*{\mathrm{\mathbb{E}}}_{1\leq n\leq N} 1_{C_{\varepsilon}}(n)\lVert F_{\varepsilon}-1_{B_{\varepsilon}} \rVert_{\infty} \leq 8\varepsilon +o_N(1), \end{align} $$
where we used the fact that
![]() $\mathbf {1}_{B_{\varepsilon }}(\{a_1(n)\})=F_{\varepsilon }(\{a_1(n)\})$
for all n on the complement of
$\mathbf {1}_{B_{\varepsilon }}(\{a_1(n)\})=F_{\varepsilon }(\{a_1(n)\})$
for all n on the complement of
![]() $C_{\varepsilon }$
, the trivial bound for the values of
$C_{\varepsilon }$
, the trivial bound for the values of
![]() $n\in C_{\varepsilon }$
and the fact that
$n\in C_{\varepsilon }$
and the fact that
![]() $C_{\varepsilon }$
has upper density at most
$C_{\varepsilon }$
has upper density at most
![]() $4\varepsilon $
.
$4\varepsilon $
.
Combining equations (39) and (40), we deduce that
 $$ \begin{align} &\big\lVert \underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} {\mathbf 1}_{A_0}(n)\ T^{ \left\lfloor {a_1(n)} \right\rfloor }(f_1\cdot T^{ \left\lfloor {c} \right\rfloor }f_2)\cdot T^{ \left\lfloor {a_3(n)} \right\rfloor }f_3\cdots T^{ \left\lfloor {a_k(n)} \right\rfloor } f_k \nonumber\\ &\qquad- \underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} F_{\varepsilon}(\{a_1(n)\})\ T^{ \left\lfloor {a_1(n)} \right\rfloor }(f_1\cdot T^{ \left\lfloor {c} \right\rfloor }f_2)\cdot T^{ \left\lfloor {a_3(n)} \right\rfloor }f_3\cdots T^{ \left\lfloor {a_k(n)} \right\rfloor } f_k \big\rVert_{L^2(\mu)}\nonumber\\ &\quad\leq 10\varepsilon+o_N(1). \end{align} $$
$$ \begin{align} &\big\lVert \underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} {\mathbf 1}_{A_0}(n)\ T^{ \left\lfloor {a_1(n)} \right\rfloor }(f_1\cdot T^{ \left\lfloor {c} \right\rfloor }f_2)\cdot T^{ \left\lfloor {a_3(n)} \right\rfloor }f_3\cdots T^{ \left\lfloor {a_k(n)} \right\rfloor } f_k \nonumber\\ &\qquad- \underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} F_{\varepsilon}(\{a_1(n)\})\ T^{ \left\lfloor {a_1(n)} \right\rfloor }(f_1\cdot T^{ \left\lfloor {c} \right\rfloor }f_2)\cdot T^{ \left\lfloor {a_3(n)} \right\rfloor }f_3\cdots T^{ \left\lfloor {a_k(n)} \right\rfloor } f_k \big\rVert_{L^2(\mu)}\nonumber\\ &\quad\leq 10\varepsilon+o_N(1). \end{align} $$
Taking
![]() $\varepsilon \to 0$
, we deduce that it is sufficient to verify that the averages
$\varepsilon \to 0$
, we deduce that it is sufficient to verify that the averages
converge for any continuous function F on
![]() $\mathbb {T}$
. This would imply that the averages
$\mathbb {T}$
. This would imply that the averages
converge in norm.
After approximating F by trigonometric polynomials (in the uniform norm), it suffices to show that the averages
converge in norm for any
![]() $l_1\in \mathbb {Z}$
. Note that the function
$l_1\in \mathbb {Z}$
. Note that the function
![]() $a_2(t)$
has vanished and its role has been replaced by the sequence
$a_2(t)$
has vanished and its role has been replaced by the sequence
![]() $e(l_1a_1(n))$
.
$e(l_1a_1(n))$
.
We repeat this process until we eliminate all pairs of functions, whose difference grows slower than
![]() $\log t$
, where at each step, our averages are multiplied by a sequence of the form
$\log t$
, where at each step, our averages are multiplied by a sequence of the form
![]() $e(l_ia_i(n))$
(
$e(l_ia_i(n))$
(
![]() $l_i\in \mathbb {Z}$
). After finitely many iterations, our problem eventually reduces to the following: let
$l_i\in \mathbb {Z}$
). After finitely many iterations, our problem eventually reduces to the following: let
![]() $a_1,\ldots ,a_k$
satisfy equation (8) or equation (9) and let
$a_1,\ldots ,a_k$
satisfy equation (8) or equation (9) and let
![]() $b_1,\ldots ,b_m$
be a subset of
$b_1,\ldots ,b_m$
be a subset of
![]() $\{a_1,\ldots ,a_k\}$
, so that the functions
$\{a_1,\ldots ,a_k\}$
, so that the functions
![]() $b_1,\ldots ,b_m$
satisfy the hypotheses of Proposition 4.3. Then, for any integers
$b_1,\ldots ,b_m$
satisfy the hypotheses of Proposition 4.3. Then, for any integers
![]() $l_1,\ldots l_k$
, the averages
$l_1,\ldots l_k$
, the averages
converge in
![]() $L^2(\mu )$
for all functions
$L^2(\mu )$
for all functions
![]() $f_1,\ldots , f_m\in L^{\infty }(\mu )$
.
$f_1,\ldots , f_m\in L^{\infty }(\mu )$
.
Now we can apply Proposition 4.3 and use a standard telescopic argument to show that the limiting behaviour of the above averages does not change if we replace the functions
![]() $f_i$
by their projections to the factor
$f_i$
by their projections to the factor
![]() $Z_s(X)$
(the number s is the one given by Proposition 4.3). However, by Theorem E, the factors
$Z_s(X)$
(the number s is the one given by Proposition 4.3). However, by Theorem E, the factors
![]() $Z_s(X)$
are inverse limits of s-step nilsystems. Thus, by another standard limiting argument, we may reduce to the case that the space X is a nilmanifold and
$Z_s(X)$
are inverse limits of s-step nilsystems. Thus, by another standard limiting argument, we may reduce to the case that the space X is a nilmanifold and
![]() $\mu $
is its Haar measure, while the transformation T is the action (by left multiplication) of an element g on X. Finally, we can approximate the functions
$\mu $
is its Haar measure, while the transformation T is the action (by left multiplication) of an element g on X. Finally, we can approximate the functions
![]() $f_i$
by continuous functions and reduce our problem to the following.
$f_i$
by continuous functions and reduce our problem to the following.
If
![]() $X=G/\Gamma $
is a nilmanifold with
$X=G/\Gamma $
is a nilmanifold with
![]() $g\in G$
and the functions
$g\in G$
and the functions
![]() $a_1,\ldots ,a_k,b_1,\ldots , b_m\in \mathcal {H}$
are as above, then for any continuous functions
$a_1,\ldots ,a_k,b_1,\ldots , b_m\in \mathcal {H}$
are as above, then for any continuous functions
![]() $f_1,\ldots ,f_m$
, the averages
$f_1,\ldots ,f_m$
, the averages
converge in mean.
We show that these averages converge pointwise for every
![]() $x\in X$
. We recall that the functions
$x\in X$
. We recall that the functions
![]() $b_1,\ldots ,b_m$
belong to the set
$b_1,\ldots ,b_m$
belong to the set
![]() $\{a_1,\ldots ,a_k\}$
(this is the only thing that we will need to use for the rest of the proof).
$\{a_1,\ldots ,a_k\}$
(this is the only thing that we will need to use for the rest of the proof).
First of all, it suffices to show that the averages
converge pointwise, where
![]() $X=G/\Gamma $
is such that G is connected, simply connected nilpotent Lie group (basically, we can remove the integer parts appearing in the iterates). This follows by standard modifications in the proof of Lemma 3.2 (the fact that we have the coefficients
$X=G/\Gamma $
is such that G is connected, simply connected nilpotent Lie group (basically, we can remove the integer parts appearing in the iterates). This follows by standard modifications in the proof of Lemma 3.2 (the fact that we have the coefficients
![]() $e(l_1a_1(n)+\cdots +l_ka_k(n))$
in the final expression does not affect the argument), so we omit the details.
$e(l_1a_1(n)+\cdots +l_ka_k(n))$
in the final expression does not affect the argument), so we omit the details.
Now, observe that we can write the above averages in the form
where
![]() $g_0=(1_{\mathbb {T}},e_G)$
and
$g_0=(1_{\mathbb {T}},e_G)$
and
![]() $\tilde {g}=(1_{\mathbb {T}},g)$
act on the product nilmanifold
$\tilde {g}=(1_{\mathbb {T}},g)$
act on the product nilmanifold
![]() $\mathbb {T}\times X$
, the point
$\mathbb {T}\times X$
, the point
![]() $\tilde {x}$
is just
$\tilde {x}$
is just
![]() $(\mathbb {Z},x)$
and the functions
$(\mathbb {Z},x)$
and the functions
![]() $F_i$
are defined by
$F_i$
are defined by
These are continuous functions on
![]() $\mathbb {T}\times X$
. The functions
$\mathbb {T}\times X$
. The functions
![]() $l_1a_1(t)+\cdots +l_ka_k(t), b_1(t),\ldots ,b_m(t)$
satisfy the hypotheses of Theorem 1.2 (since the functions
$l_1a_1(t)+\cdots +l_ka_k(t), b_1(t),\ldots ,b_m(t)$
satisfy the hypotheses of Theorem 1.2 (since the functions
![]() $a_1,\ldots ,a_k$
do) and the result follows.
$a_1,\ldots ,a_k$
do) and the result follows.
Acknowledgements
I would like to thank my PhD advisor Nikos Frantzikinakis for many helpful discussions. I would also like to thank the anonymous referee for pointing out corrections in the previous versions of the paper and for several additional valuable suggestions that improved the overall presentation of the article. The author was supported by the Research Grant ELIDEK HFRI-FM17-1684 and ELIDEK-Fellowship number 5367 (3rd Call for HFRI Ph.D. Fellowships) during the preparation of this article.
A Appendix. Hardy field functions in short intervals
A.1 Growth rates of Hardy field functions
All of the results presented below were proven in [Reference Tsinas18] and thus we omit their proofs. We refer the reader to the example in §3, where we establish Theorem 1.2 in the case where we have two simple functions. In that example, we do not need any special lemmas to show that we can find a common Taylor expansion, because we can perform the calculations by hand. However, in the proofs of Theorems 1.1 and 1.2, we need to show that we can always do the same common polynomial expansion for general functions.
The first two propositions are some elementary facts concerning the growth rates of derivatives of functions in a Hardy field.
Proposition A.1. [Reference Tsinas18, Proposition A.1]
Let
![]() $f\in \mathcal {H}$
have polynomial growth. Then, for any natural number k, we have
$f\in \mathcal {H}$
have polynomial growth. Then, for any natural number k, we have
In addition, if
![]() $ t^{\delta }\prec f(t)$
for some
$ t^{\delta }\prec f(t)$
for some
![]() $\delta>0$
, we have
$\delta>0$
, we have
The above proposition establishes that if we have a function in
![]() $\mathcal {H}$
that has polynomial growth, then its derivatives of large enough order will be functions that converge to 0. The next lemma implies that a particular growth relation holds between consecutive derivatives (of large enough order).
$\mathcal {H}$
that has polynomial growth, then its derivatives of large enough order will be functions that converge to 0. The next lemma implies that a particular growth relation holds between consecutive derivatives (of large enough order).
Proposition A.2. [Reference Tsinas18, Proposition A.2]
Let
![]() $f\in \mathcal {H}$
be strongly non-polynomial with
$f\in \mathcal {H}$
be strongly non-polynomial with
![]() $f(t)\succ \log t$
. Then, for k sufficiently large, we have
$f(t)\succ \log t$
. Then, for k sufficiently large, we have
Let us demonstrate how this proposition is used to get a polynomial expansion in short intervals for a single function. Let
![]() $a\in \mathcal {H}$
be a strongly non-polynomial function that satisfies the growth condition
$a\in \mathcal {H}$
be a strongly non-polynomial function that satisfies the growth condition
![]() $a(t)\succ \log t$
. Let k be a positive integer that is large enough so that we can apply the two preceding propositions. We argue that we can find a function
$a(t)\succ \log t$
. Let k be a positive integer that is large enough so that we can apply the two preceding propositions. We argue that we can find a function
![]() $L(t)$
(not necessarily in
$L(t)$
(not necessarily in
![]() $\mathcal {H}$
) such that
$\mathcal {H}$
) such that
For instance, the geometric mean of the functions
![]() $|a^{(k)}(t)|^{-1/k}$
and
$|a^{(k)}(t)|^{-1/k}$
and
![]() $|a^{(k+1)}(t)|^{-1/(k+1)}$
is a suitable choice for our purposes.
$|a^{(k+1)}(t)|^{-1/(k+1)}$
is a suitable choice for our purposes.
We will examine the function a in intervals of the form
![]() $[N, N+L(N)]$
and approximate it by a polynomial, which will vary with N. Observe that if
$[N, N+L(N)]$
and approximate it by a polynomial, which will vary with N. Observe that if
![]() $0\leq h\leq L(N)$
, then we have
$0\leq h\leq L(N)$
, then we have
 $$ \begin{align*} a(N+h)=a(N)+\cdots+\frac{h^ka^{(k)}(N)}{k!} +\frac{h^{k+1}a^{(k+1)}(\xi_{h,N})}{(k+1)!} \end{align*} $$
$$ \begin{align*} a(N+h)=a(N)+\cdots+\frac{h^ka^{(k)}(N)}{k!} +\frac{h^{k+1}a^{(k+1)}(\xi_{h,N})}{(k+1)!} \end{align*} $$
for some
![]() $\xi _{h,N} \in [N,N+h]$
. Using the largeness of k, Proposition A.2 implies that
$\xi _{h,N} \in [N,N+h]$
. Using the largeness of k, Proposition A.2 implies that
![]() $|a^{(k+1)}(t)|\to 0$
monotonically (the monotonicity follows from the fact that the function
$|a^{(k+1)}(t)|\to 0$
monotonically (the monotonicity follows from the fact that the function
![]() $a^{(k+1)}(t)$
belongs to
$a^{(k+1)}(t)$
belongs to
![]() $\mathcal {H}$
). Then, for N sufficiently large,
$\mathcal {H}$
). Then, for N sufficiently large,
 $$ \begin{align*} \bigg|\frac{h^{k+1}a^{(k+1)}(\xi_{h,N})}{(k+1)!}\bigg|\leq\bigg| \frac{L(N)^{k+1}a^{(k+1)}(N)}{(k+1)!}\bigg|\prec 1, \end{align*} $$
$$ \begin{align*} \bigg|\frac{h^{k+1}a^{(k+1)}(\xi_{h,N})}{(k+1)!}\bigg|\leq\bigg| \frac{L(N)^{k+1}a^{(k+1)}(N)}{(k+1)!}\bigg|\prec 1, \end{align*} $$
because of equation (A.1). Furthermore, we have that
 $$ \begin{align*} \bigg|\frac{L(N)^{k}a^{(k)}(N+L(N))}{k!}\bigg|\to +\infty. \end{align*} $$
$$ \begin{align*} \bigg|\frac{L(N)^{k}a^{(k)}(N+L(N))}{k!}\bigg|\to +\infty. \end{align*} $$
Indeed, since
![]() $L(t)$
is a sub-linear function by Proposition A.2, we infer that the two functions
$L(t)$
is a sub-linear function by Proposition A.2, we infer that the two functions
![]() $a^{(k)}(t+L(t))$
and
$a^{(k)}(t+L(t))$
and
![]() $a^{(k)}(t)$
have the same growth rate and thus we only need to prove that
$a^{(k)}(t)$
have the same growth rate and thus we only need to prove that
 $$ \begin{align} \bigg|\frac{L(N)^{k}a^{(k)}(N)}{k!}\bigg|\to +\infty. \end{align} $$
$$ \begin{align} \bigg|\frac{L(N)^{k}a^{(k)}(N)}{k!}\bigg|\to +\infty. \end{align} $$
This follows similarly as above. To summarize, we have
Therefore, functions that satisfy equation (A.1) have the following distinctive property: the sequence
![]() $a(n)$
, when restricted to the intervals
$a(n)$
, when restricted to the intervals
![]() $[N, N+L(N)]$
as above, is asymptotically equal to a polynomial sequence (that depends on N) of degree exactly k. This motivates us to study the properties of functions that satisfy equation (A.1). The main goal is to accomplish the same for several functions
$[N, N+L(N)]$
as above, is asymptotically equal to a polynomial sequence (that depends on N) of degree exactly k. This motivates us to study the properties of functions that satisfy equation (A.1). The main goal is to accomplish the same for several functions
![]() $a_1,\ldots , a_{m}$
in a Hardy field
$a_1,\ldots , a_{m}$
in a Hardy field
![]() $\mathcal {H}$
. This is relatively straightforward to do by hand in explicit examples, like the one in §3. In the more abstract setting, if we manage to show that we can find a function
$\mathcal {H}$
. This is relatively straightforward to do by hand in explicit examples, like the one in §3. In the more abstract setting, if we manage to show that we can find a function
![]() $L(t)$
, so that equation (A.1) is satisfied for all functions
$L(t)$
, so that equation (A.1) is satisfied for all functions
![]() $a_1,\ldots , a_{m}$
(the integer k is allowed to be different for each function), then we will establish that a polynomial expansion like the one in equation (A.3) holds for all the functions
$a_1,\ldots , a_{m}$
(the integer k is allowed to be different for each function), then we will establish that a polynomial expansion like the one in equation (A.3) holds for all the functions
![]() $a_1,\ldots , a_{m}$
simultaneously. We will introduce some notions shortly that will assist us in this endeavour.
$a_1,\ldots , a_{m}$
simultaneously. We will introduce some notions shortly that will assist us in this endeavour.
A.2 The sub-classes
 $S(a,k)$
$S(a,k)$
Let
![]() $a\in \mathcal {H}$
be a strongly non-polynomial function such that
$a\in \mathcal {H}$
be a strongly non-polynomial function such that
![]() $a(t)\gg t^{\delta }$
, for some
$a(t)\gg t^{\delta }$
, for some
![]() $\delta>0$
(namely, we exclude sub-fractional functions). For
$\delta>0$
(namely, we exclude sub-fractional functions). For
![]() $k\in \mathbb {N}$
sufficiently large (we only require that
$k\in \mathbb {N}$
sufficiently large (we only require that
![]() $a^{(k)}(t)\to 0$
), we define the subclass
$a^{(k)}(t)\to 0$
), we define the subclass
![]() $S(a,k)$
of
$S(a,k)$
of
![]() $\mathcal {H}$
as
$\mathcal {H}$
as
where the notation
![]() $g(t)\preceq f(t)$
signifies that the limit
$g(t)\preceq f(t)$
signifies that the limit
![]() $\lim \nolimits _{t\to \infty } |f(t)/g(t)|$
is non-zero. The purpose of the classes
$\lim \nolimits _{t\to \infty } |f(t)/g(t)|$
is non-zero. The purpose of the classes
![]() $S(a,k)$
is to characterize the growth relation in equation (A.1). We will use the following lemma.
$S(a,k)$
is to characterize the growth relation in equation (A.1). We will use the following lemma.
Lemma A.3. [Reference Tsinas18, Lemma A.3]
Let
![]() $a\in \mathcal {H}$
be a strongly non-polynomial function with
$a\in \mathcal {H}$
be a strongly non-polynomial function with
![]() $a(t)\gg t^{\delta }$
, for some
$a(t)\gg t^{\delta }$
, for some
![]() $\delta>0$
.
$\delta>0$
.
-
(i) The class
 $S(a,k)$
is non-empty for k sufficiently large.
$S(a,k)$
is non-empty for k sufficiently large. -
(ii) For any
 $0< c< 1$
sufficiently close to 1, there exists
$0< c< 1$
sufficiently close to 1, there exists
 $k_0\in \mathbb {N}$
(depending on c), such that the function
$k_0\in \mathbb {N}$
(depending on c), such that the function
 $t\to t^c$
belongs to
$t\to t^c$
belongs to
 $S(a,k_0)$
.
$S(a,k_0)$
. -
(iii) The class
 $S(a,k)$
does not contain all functions of the form
$S(a,k)$
does not contain all functions of the form
 $t\to t^c$
for c sufficiently close to 1.
$t\to t^c$
for c sufficiently close to 1.
A naive way to think of the sub-classes is like a sequence of disjoint intervals on a line (with no gaps between consecutive intervals). Property (ii) in the above lemma implies that each function of the form
![]() $t^c$
for c close to 1 belongs to a unique
$t^c$
for c close to 1 belongs to a unique
![]() $S(a,k)$
. We can demonstrate that this actually holds if the fractional power
$S(a,k)$
. We can demonstrate that this actually holds if the fractional power
![]() $t^c$
is replaced by any function g satisfying a growth condition of the form
$t^c$
is replaced by any function g satisfying a growth condition of the form
![]() $t^{c_1}\prec g(t)\prec t^{c_2}$
, where
$t^{c_1}\prec g(t)\prec t^{c_2}$
, where
![]() $c_1$
must be sufficiently close to 1.
$c_1$
must be sufficiently close to 1.
Proposition A.4. Let
![]() $a_1,\ldots , a_k$
be strongly non-polynomial functions in
$a_1,\ldots , a_k$
be strongly non-polynomial functions in
![]() $\mathcal {H}$
of polynomial growth, such that all the functions
$\mathcal {H}$
of polynomial growth, such that all the functions
![]() $a_i$
dominate some fractional power
$a_i$
dominate some fractional power
![]() $t^{\delta }$
for some
$t^{\delta }$
for some
![]() $\delta>0$
. There exists
$\delta>0$
. There exists
![]() $0<C<1$
depending only on the functions
$0<C<1$
depending only on the functions
![]() $a_1,\ldots ,a_k$
, such that if the function
$a_1,\ldots ,a_k$
, such that if the function
![]() $L(t)$
satisfies
$L(t)$
satisfies
for some
![]() $\varepsilon>0$
, then there exist positive integers
$\varepsilon>0$
, then there exist positive integers
![]() $k_i$
(that depend on
$k_i$
(that depend on
![]() $L(t)$
), such that
$L(t)$
), such that
![]() $L(t)\in S(a_i,k_i)$
for every
$L(t)\in S(a_i,k_i)$
for every
![]() $i\in \{1,\ldots ,k\}$
. In addition, for any positive real number M, there exists a constant
$i\in \{1,\ldots ,k\}$
. In addition, for any positive real number M, there exists a constant
![]() $A=A(M,a_1,\ldots ,a_k)\in (0,1)$
, such that if
$A=A(M,a_1,\ldots ,a_k)\in (0,1)$
, such that if
for some
![]() $\varepsilon>0$
, then we have
$\varepsilon>0$
, then we have
![]() $k_i>M$
for every
$k_i>M$
for every
![]() $i\in \{1,\ldots , k\}$
.
$i\in \{1,\ldots , k\}$
.
Proof. It is apparent that we only need to establish the assertion in the case
![]() $k=1$
(namely, when we have only one function). Therefore, we fix a strongly non-polynomial function a that is not sub-fractional and recall that by Lemma A.3, there exists a constant
$k=1$
(namely, when we have only one function). Therefore, we fix a strongly non-polynomial function a that is not sub-fractional and recall that by Lemma A.3, there exists a constant
![]() $C<1$
depending only on
$C<1$
depending only on
![]() $a(t)$
, such that every function of the form
$a(t)$
, such that every function of the form
![]() $t^c$
with
$t^c$
with
![]() $c>C$
belongs to the class
$c>C$
belongs to the class
![]() $S(a, n_c)$
for some natural number
$S(a, n_c)$
for some natural number
![]() $n_c$
. Now, assume that the function
$n_c$
. Now, assume that the function
![]() $L(t)$
satisfies
$L(t)$
satisfies
for some
![]() $C<c_1<1$
. Then, because both
$C<c_1<1$
. Then, because both
![]() $t^{C}$
and
$t^{C}$
and
![]() $t^{c_1}$
belong to the sub-classes
$t^{c_1}$
belong to the sub-classes
![]() $S(a,n_{C})$
and
$S(a,n_{C})$
and
![]() $S(a,n_{c_1})$
, respectively, for some
$S(a,n_{c_1})$
, respectively, for some
![]() $n_C,n_{c_1}\in \mathbb {N}$
, we get that
$n_C,n_{c_1}\in \mathbb {N}$
, we get that
![]() $L(t)$
belongs to
$L(t)$
belongs to
![]() $S(a,n_3)$
for some integer
$S(a,n_3)$
for some integer
![]() $n_3$
that satisfies
$n_3$
that satisfies
![]() $n_C\leq n_3\leq n_{c_1}$
.
$n_C\leq n_3\leq n_{c_1}$
.
Now we establish the second part. Let M be a fixed real number and consider a fractional power
![]() $t^{c_2}$
with
$t^{c_2}$
with
![]() $C<c_2<1$
, so that
$C<c_2<1$
, so that
![]() $t^{c_2}$
belongs to
$t^{c_2}$
belongs to
![]() $S(a,n_{c_2})$
for some
$S(a,n_{c_2})$
for some
![]() $c_2>M$
. Such a fractional power exists, which is evident by combining the second and third statements of Lemma A.3. Thus, if
$c_2>M$
. Such a fractional power exists, which is evident by combining the second and third statements of Lemma A.3. Thus, if
![]() $L(t)$
satisfies
$L(t)$
satisfies
for some
![]() $\varepsilon>0$
, we have that
$\varepsilon>0$
, we have that
![]() $L(t)\in S(a,k')$
(by the first part) for a positive integer
$L(t)\in S(a,k')$
(by the first part) for a positive integer
![]() $k'$
with
$k'$
with
![]() $k'\geq n_{c_2}>M$
. The claim follows.
$k'\geq n_{c_2}>M$
. The claim follows.
The first part of Proposition A.4 implies that if we are given functions
![]() $a_1,\ldots ,a_k$
that satisfy the hypotheses, then we can find a sub-linear function
$a_1,\ldots ,a_k$
that satisfy the hypotheses, then we can find a sub-linear function
![]() $L(t)$
, such that
$L(t)$
, such that
![]() $L(t)\in S(a_i,k_i)$
. This asserts that the function
$L(t)\in S(a_i,k_i)$
. This asserts that the function
![]() $a_i$
will be approximated by a polynomial of degree
$a_i$
will be approximated by a polynomial of degree
![]() $k_i$
in short intervals of the form
$k_i$
in short intervals of the form
![]() $[N, N+L(N)]$
for every
$[N, N+L(N)]$
for every
![]() $i\in \{1,\ldots ,k\}$
. Furthermore, the second part establishes that we can make the degrees
$i\in \{1,\ldots ,k\}$
. Furthermore, the second part establishes that we can make the degrees
![]() $k_i$
of the Taylor polynomials arbitrarily large, as long as we take the function
$k_i$
of the Taylor polynomials arbitrarily large, as long as we take the function
![]() $L(t)$
to grow ‘sufficiently fast’ (faster than some appropriate power
$L(t)$
to grow ‘sufficiently fast’ (faster than some appropriate power
![]() $t^C$
with
$t^C$
with
![]() $C<1$
).
$C<1$
).
The sub-classes
![]() $S(a,k)$
were defined for functions that are not sub-fractional. The above argument does not extend to these latter functions. As an example, let us fix a number
$S(a,k)$
were defined for functions that are not sub-fractional. The above argument does not extend to these latter functions. As an example, let us fix a number
![]() $\delta $
with
$\delta $
with
![]() $0<\delta <1$
and a sub-fractional function
$0<\delta <1$
and a sub-fractional function
![]() $a\in \mathcal {H}$
. If we consider the function
$a\in \mathcal {H}$
. If we consider the function
![]() $L(t)=t^{\delta }$
and try to repeat the same approximations to obtain an analogue of equation (A.3), we run into an issue. Clearly, it is easy to see that
$L(t)=t^{\delta }$
and try to repeat the same approximations to obtain an analogue of equation (A.3), we run into an issue. Clearly, it is easy to see that
using the mean value theorem. Thus, the sequence
![]() $a(n)$
, when it is restricted to the interval
$a(n)$
, when it is restricted to the interval
![]() $[N, N+L(N)]$
, is
$[N, N+L(N)]$
, is
![]() $o_N(1)$
close to the value
$o_N(1)$
close to the value
![]() $a(N)$
, which signifies that it is approximately equal to a constant on this interval (or equivalently, all polynomial expansions we get are of degree 0). This could be circumvented if we considered sub-linear functions
$a(N)$
, which signifies that it is approximately equal to a constant on this interval (or equivalently, all polynomial expansions we get are of degree 0). This could be circumvented if we considered sub-linear functions
![]() $L(t)$
that grow faster than all the powers
$L(t)$
that grow faster than all the powers
![]() $t^{\delta }, 0<\delta <1$
, such as the function
$t^{\delta }, 0<\delta <1$
, such as the function
![]() $t/ \log t$
. If we do this however, the growth condition in equation (A.1) can never hold for functions that are not sub-fractional (in simple terms, there can be no polynomial approximation of finite degree). (Concerning the problem of finding characteristic factors for ergodic averages involving Hardy field iterates, there was a workaround for this issue in [Reference Tsinas18] using a double-averaging trick. Unfortunately, the same argument breaks down in the setting of pointwise convergence on nilmanifolds. See also Remark 4.) We omit the specific details of this deduction.
$t/ \log t$
. If we do this however, the growth condition in equation (A.1) can never hold for functions that are not sub-fractional (in simple terms, there can be no polynomial approximation of finite degree). (Concerning the problem of finding characteristic factors for ergodic averages involving Hardy field iterates, there was a workaround for this issue in [Reference Tsinas18] using a double-averaging trick. Unfortunately, the same argument breaks down in the setting of pointwise convergence on nilmanifolds. See also Remark 4.) We omit the specific details of this deduction.
A.3 Decomposing Hardy field functions
We consider a Hardy field
![]() $\mathcal {H}$
that contains the polynomials and let a be a function in
$\mathcal {H}$
that contains the polynomials and let a be a function in
![]() $\mathcal {H}$
. We partition
$\mathcal {H}$
. We partition
![]() $\mathcal {H}$
into equivalence classes by the relation
$\mathcal {H}$
into equivalence classes by the relation
![]() $f\sim g$
, which is equivalent to saying that the limit of
$f\sim g$
, which is equivalent to saying that the limit of
![]() $f(t)/g(t)$
as
$f(t)/g(t)$
as
![]() $t\to +\infty $
is a non-zero real number. In simple terms,
$t\to +\infty $
is a non-zero real number. In simple terms,
![]() $f,g$
are in the same equivalence class if and only if they have the same growth rate. We put the zero function in its own equivalence class.
$f,g$
are in the same equivalence class if and only if they have the same growth rate. We put the zero function in its own equivalence class.
We will define the strongly non-polynomial growth rate of a function
![]() $a\in \mathcal {H}$
as follows.
$a\in \mathcal {H}$
as follows.
(i) If a is a strongly non-polynomial function (recall the definition in §2), we define it to be the equivalence class of a.
(ii) If a is not strongly non-polynomial, then it can be written in the form
![]() $p(t)+x(t)$
, where
$p(t)+x(t)$
, where
![]() $p(t)$
is a polynomial and
$p(t)$
is a polynomial and
![]() $x(t)$
is a strongly non-polynomial function (or the zero function) with
$x(t)$
is a strongly non-polynomial function (or the zero function) with
![]() $x(t)\prec p(t)$
. Observe that
$x(t)\prec p(t)$
. Observe that
![]() $x(t)$
is a function in
$x(t)$
is a function in
![]() $\mathcal {H},$
since our Hardy field contains the polynomials. We define the strongly non-polynomial growth rate of a as the equivalence class of the function
$\mathcal {H},$
since our Hardy field contains the polynomials. We define the strongly non-polynomial growth rate of a as the equivalence class of the function
![]() $x\in \mathcal {H}$
.
$x\in \mathcal {H}$
.
The strongly non-polynomial growth rate is defined for any function
![]() $a\in \mathcal {H}$
. It is well defined, in the following sense: consider a function
$a\in \mathcal {H}$
. It is well defined, in the following sense: consider a function
![]() $a\in \mathcal {H}$
like in case (ii) above, which has two different representations as
$a\in \mathcal {H}$
like in case (ii) above, which has two different representations as
![]() $p_1(t)+x_1(t)$
and
$p_1(t)+x_1(t)$
and
![]() $p_2(t)+x_2(t)$
, where
$p_2(t)+x_2(t)$
, where
![]() $p_1,p_2$
are polynomials,
$p_1,p_2$
are polynomials,
![]() $x_1,x_2$
are strongly non-polynomial, and
$x_1,x_2$
are strongly non-polynomial, and
![]() $x_1(t)\prec p_1(t)$
and
$x_1(t)\prec p_1(t)$
and
![]() $x_2(t)\prec p_2(t)$
. Then, we must have
$x_2(t)\prec p_2(t)$
. Then, we must have
![]() $x_1(t)\sim x_2(t)$
. An example where such distinct representations may exist is the function
$x_1(t)\sim x_2(t)$
. An example where such distinct representations may exist is the function
![]() $a(t)=t^2+t+t^{3/2}$
. We can choose
$a(t)=t^2+t+t^{3/2}$
. We can choose
![]() $p_1(t)=t^2,x_1(t)=t^{3/2}+t$
and
$p_1(t)=t^2,x_1(t)=t^{3/2}+t$
and
![]() $p_2(t)=t^2+t,x_2(t)=t^{3/2}$
. While
$p_2(t)=t^2+t,x_2(t)=t^{3/2}$
. While
![]() $x_1\neq x_2$
, these two functions have the same growth rate.
$x_1\neq x_2$
, these two functions have the same growth rate.
A simple observation is that if a function
![]() $a\in \mathcal {H}$
is written in the form
$a\in \mathcal {H}$
is written in the form
![]() $p(t)+x(t)$
, where p is polynomial and x is strongly non-polynomial, then the functions a and x have the same strongly non-polynomial growth rate (one could alternatively use this remark to present another equivalent definition of the strongly non-polynomial growth rate).
$p(t)+x(t)$
, where p is polynomial and x is strongly non-polynomial, then the functions a and x have the same strongly non-polynomial growth rate (one could alternatively use this remark to present another equivalent definition of the strongly non-polynomial growth rate).
Finally, we also say that
![]() $a\in \mathcal {H}$
has trivial growth rate if
$a\in \mathcal {H}$
has trivial growth rate if
![]() $\lim \nolimits _{t\to +\infty }a(t)=0$
. Recall that we also included these functions when we defined the strongly non-polynomial functions. We will now prove the following lemma.
$\lim \nolimits _{t\to +\infty }a(t)=0$
. Recall that we also included these functions when we defined the strongly non-polynomial functions. We will now prove the following lemma.
Lemma A.5. Let
![]() $\mathcal {H}$
be a Hardy field that contains the polynomials and let
$\mathcal {H}$
be a Hardy field that contains the polynomials and let
![]() $a_1,\ldots , a_k\in \mathcal {H}$
be arbitrary functions. Then, the set
$a_1,\ldots , a_k\in \mathcal {H}$
be arbitrary functions. Then, the set
![]() $\mathcal {L}(a_1,\ldots ,a_k)$
of non-trivial linear combinations has a basis
$\mathcal {L}(a_1,\ldots ,a_k)$
of non-trivial linear combinations has a basis
![]() $(g_1,\ldots ,g_m,h_1,\ldots ,h_{\ell })$
, where
$(g_1,\ldots ,g_m,h_1,\ldots ,h_{\ell })$
, where
![]() $m,\ell $
are non-negative integers, such that the functions
$m,\ell $
are non-negative integers, such that the functions
![]() $h_1,\ldots ,h_{\ell }$
have the form
$h_1,\ldots ,h_{\ell }$
have the form
![]() $p_i(t)+o_t(1)$
, where
$p_i(t)+o_t(1)$
, where
![]() $p_i$
is a real polynomial for every
$p_i$
is a real polynomial for every
![]() $ 1\leq i\leq \ell $
and
$ 1\leq i\leq \ell $
and
![]() $g_1,\ldots ,g_m$
have distinct and non-trivial strongly non-polynomial growth rates.
$g_1,\ldots ,g_m$
have distinct and non-trivial strongly non-polynomial growth rates.
Proof. We can restrict our attention to the case that the functions
![]() $a_1,\ldots ,a_k$
are linearly independent (otherwise, we pass to a maximal subset of these functions whose elements are linearly independent). We induct on k. For
$a_1,\ldots ,a_k$
are linearly independent (otherwise, we pass to a maximal subset of these functions whose elements are linearly independent). We induct on k. For
![]() $k=1$
, we have nothing to prove. Assume the claim holds for all integers smaller than k. All functions considered below are implicitly assumed to belong to
$k=1$
, we have nothing to prove. Assume the claim holds for all integers smaller than k. All functions considered below are implicitly assumed to belong to
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
We may write each of the functions
![]() $a_1,\ldots ,a_k$
in the form
$a_1,\ldots ,a_k$
in the form
![]() $p_i(t)+x_i(t)$
, where
$p_i(t)+x_i(t)$
, where
![]() $p_i$
are real polynomials and
$p_i$
are real polynomials and
![]() $x_i(t)$
are strongly non-polynomial functions (either one of the functions
$x_i(t)$
are strongly non-polynomial functions (either one of the functions
![]() $p_i,x_i$
may also be identically zero). After reordering, we may assume that
$p_i,x_i$
may also be identically zero). After reordering, we may assume that
Now, we define the number
![]() $l\in \{0,1,\ldots ,k\}$
to be the smallest natural number for which all functions
$l\in \{0,1,\ldots ,k\}$
to be the smallest natural number for which all functions
![]() $x_{l+1}(t),x_{l+2}(t)$
and so on have limit zero (as
$x_{l+1}(t),x_{l+2}(t)$
and so on have limit zero (as
![]() $t\to +\infty $
). If none of the
$t\to +\infty $
). If none of the
![]() $x_i$
have limits going to
$x_i$
have limits going to
![]() $0$
, then we just set
$0$
, then we just set
![]() $\ell =k$
.
$\ell =k$
.
We consider two cases.
(i) If the functions
![]() $x_1,\ldots ,x_{l}$
have distinct growth rates, then we are done. In this case, the functions
$x_1,\ldots ,x_{l}$
have distinct growth rates, then we are done. In this case, the functions
![]() $g_j$
appearing in the statement are the functions
$g_j$
appearing in the statement are the functions
![]() $p_i(t)+x_i(t)$
for
$p_i(t)+x_i(t)$
for
![]() $1\leq i\leq l$
, while the role of the functions
$1\leq i\leq l$
, while the role of the functions
![]() $h_j$
is performed by the functions
$h_j$
is performed by the functions
![]() $p_i(t)+x_i(t)$
for
$p_i(t)+x_i(t)$
for
![]() $i>l$
(observe that for
$i>l$
(observe that for
![]() $i>l$
, we have that
$i>l$
, we have that
![]() $x_i(t)$
have trivial growth rate due to the definition of l). The strongly non-polynomial growth rates of the former set of functions are equal to the growth rates of the functions
$x_i(t)$
have trivial growth rate due to the definition of l). The strongly non-polynomial growth rates of the former set of functions are equal to the growth rates of the functions
![]() $x_1,\ldots ,x_{l}$
, which are pairwise distinct.
$x_1,\ldots ,x_{l}$
, which are pairwise distinct.
(ii) Assume now two of the functions among
![]() $x_1,\ldots ,x_l$
have the same growth rate. In particular, let
$x_1,\ldots ,x_l$
have the same growth rate. In particular, let
![]() $k_0$
be the smallest integer such that
$k_0$
be the smallest integer such that
![]() $x_{k_0}\sim x_{k_0+1}$
(obviously
$x_{k_0}\sim x_{k_0+1}$
(obviously
![]() $k_0<l$
) and let
$k_0<l$
) and let
![]() $r\geq 1$
be the largest integer such that
$r\geq 1$
be the largest integer such that
For
![]() $k_0+1\leq i\leq k_0+r$
, we can write
$k_0+1\leq i\leq k_0+r$
, we can write
![]() $x_i(t)=x_{k_0}(t)+y_i(t)$
, where
$x_i(t)=x_{k_0}(t)+y_i(t)$
, where
![]() $y_i(t)\prec x_i(t)$
. Using this, we can write
$y_i(t)\prec x_i(t)$
. Using this, we can write
![]() $a_{k_0}(t)=p_{k_0}(t)+x_{k_0}(t)$
and
$a_{k_0}(t)=p_{k_0}(t)+x_{k_0}(t)$
and
Now we apply the induction hypothesis on the collection of functions
 $$ \begin{align*} \{ p_{k_0+1}(t)-p_{k_0}(t)+y_{k_0+1}(t),\ldots, &\, p_{k_0+r}(t)-p_{k_0}(t)+y_{k_0+r}(t),\\ &\qquad p_{k_0+r+1}(t)+x_{k_0+r+1}(t),\ldots,p_{k}(t)+x_k(t)\}. \end{align*} $$
$$ \begin{align*} \{ p_{k_0+1}(t)-p_{k_0}(t)+y_{k_0+1}(t),\ldots, &\, p_{k_0+r}(t)-p_{k_0}(t)+y_{k_0+r}(t),\\ &\qquad p_{k_0+r+1}(t)+x_{k_0+r+1}(t),\ldots,p_{k}(t)+x_k(t)\}. \end{align*} $$
This gives a basis
![]() $(g_1,\ldots ,g_{m},u_1,\ldots ,u_{\ell })$
for this set of functions, with the properties outlined in the statement. We add the functions
$(g_1,\ldots ,g_{m},u_1,\ldots ,u_{\ell })$
for this set of functions, with the properties outlined in the statement. We add the functions
![]() $p_1(t)+x_1(t),\ldots ,p_{k_0}(t)+x_{k_0}(t)$
to the functions
$p_1(t)+x_1(t),\ldots ,p_{k_0}(t)+x_{k_0}(t)$
to the functions
![]() $g_1,\ldots ,g_m$
and add the functions
$g_1,\ldots ,g_m$
and add the functions
![]() $p_i(t)+x_i(t)$
,
$p_i(t)+x_i(t)$
,
![]() $l<i\leq k$
, to the collection
$l<i\leq k$
, to the collection
![]() $u_1,\ldots ,u_{\ell }$
. (Recall that
$u_1,\ldots ,u_{\ell }$
. (Recall that
![]() $x_i(t)$
goes to 0 for
$x_i(t)$
goes to 0 for
![]() $l< i\leq k$
.) In this way, we construct a basis for the original collection
$l< i\leq k$
.) In this way, we construct a basis for the original collection
![]() $a_1,\ldots ,a_k$
with the asserted properties (if the functions that we have constructed are not linearly independent, then we can just pass to a subset of these functions that will form a basis). Indeed, we only have to check that the functions
$a_1,\ldots ,a_k$
with the asserted properties (if the functions that we have constructed are not linearly independent, then we can just pass to a subset of these functions that will form a basis). Indeed, we only have to check that the functions
have distinct strongly non-polynomial growth rates. This follows by noting that the strongly non-polynomial growth rates of the functions
![]() $g_1,\ldots ,g_m$
cannot be larger than the growth rates of the functions
$g_1,\ldots ,g_m$
cannot be larger than the growth rates of the functions
![]() $y_i$
, which all grow strictly slower than
$y_i$
, which all grow strictly slower than
![]() $x_{k_0}$
. Thus, the function
$x_{k_0}$
. Thus, the function
![]() $p_{k_0}(t)+x_{k_0}(t)$
has a bigger strongly non-polynomial growth rate than all of the functions
$p_{k_0}(t)+x_{k_0}(t)$
has a bigger strongly non-polynomial growth rate than all of the functions
![]() $g_1,\ldots ,g_m$
. Furthermore, the strongly non-polynomial growth rate of the function
$g_1,\ldots ,g_m$
. Furthermore, the strongly non-polynomial growth rate of the function
![]() $p_i(t)+x_i(t)\ (1\leq i\leq k_0)$
is the same as
$p_i(t)+x_i(t)\ (1\leq i\leq k_0)$
is the same as
![]() $x_i(t)$
, and these are all pairwise distinct by the definition of
$x_i(t)$
, and these are all pairwise distinct by the definition of
![]() $k_0$
. The claim follows.
$k_0$
. The claim follows.
Remark A.6.
-
(i) Note that we do not require that the functions
 $a_1,\ldots ,a_k$
have polynomial growth in the above lemma.
$a_1,\ldots ,a_k$
have polynomial growth in the above lemma. -
(ii) A very simple example that illustrates the above decomposition is the following: assume that we have the functions
 $a_1(t)=t^2+t^{3/2}, a_2(t)=t^{3/2}, a_3(t)=2t^{3/2}+t^2$
and
$a_1(t)=t^2+t^{3/2}, a_2(t)=t^{3/2}, a_3(t)=2t^{3/2}+t^2$
and
 $a_4(t)=t^{3/2}+t\log t +t^3$
. These four functions are clearly linearly dependent. The above lemma provides the basis
$a_4(t)=t^{3/2}+t\log t +t^3$
. These four functions are clearly linearly dependent. The above lemma provides the basis
 $(g_1,g_2,h_1)$
, where
$(g_1,g_2,h_1)$
, where
 $g_1(t)=t^{3/2}, g_2(t)=t\log t+t^3$
and
$g_1(t)=t^{3/2}, g_2(t)=t\log t+t^3$
and
 $ h_1(t)=t^2$
. The main property (which will be important in the proof of Theorem 1.2) is that the functions
$ h_1(t)=t^2$
. The main property (which will be important in the proof of Theorem 1.2) is that the functions
 $g_1,g_2$
have distinct strongly non-polynomial growth rates (
$g_1,g_2$
have distinct strongly non-polynomial growth rates (
 $t^{3/2},t\log t$
, respectively), even though
$t^{3/2},t\log t$
, respectively), even though
 $g_2$
grows like
$g_2$
grows like
 $t^3$
(i.e. a polynomial).
$t^3$
(i.e. a polynomial).
B Appendix. Nilmanifolds and quantitative equidistribution theory
B.1 Background on nilmanifolds
A large portion of the material concerning nilmanifolds (excluding the quantitative equidistribution results) can be found in [Reference Host and Kra12, Part 3], where there is a focus on the ergodic theoretic point of view. For a more general presentation of the theory of nilpotent Lie groups, see also [Reference Corwin and Greenleaf3].
Let G be a topological group. A subgroup H of a topological group G is called discrete if there is a cover of H by open sets of G, such that each of these open sets contains exactly one element of H. It is called co-compact if the quotient topology makes
![]() $G/H$
a compact space. We call a subgroup with both of the above properties uniform and we will use the letters
$G/H$
a compact space. We call a subgroup with both of the above properties uniform and we will use the letters
![]() $\Gamma $
or
$\Gamma $
or
![]() $\Delta $
to denote such subgroups.
$\Delta $
to denote such subgroups.
Let G be a k-step nilpotent Lie group and
![]() $\Gamma $
be a uniform subgroup. The space
$\Gamma $
be a uniform subgroup. The space
![]() $X=G/\Gamma $
is called a k-step nilmanifold.
$X=G/\Gamma $
is called a k-step nilmanifold.
Let b be any element in G. Then, b acts on G by left multiplication. Let
![]() $m_X$
be the image of the Haar measure of G on X under the natural projection map. Then,
$m_X$
be the image of the Haar measure of G on X under the natural projection map. Then,
![]() $m_X$
is invariant under the action of the element b (and therefore the action of G). If we set
$m_X$
is invariant under the action of the element b (and therefore the action of G). If we set
![]() $T(g\Gamma )=(bg)\Gamma $
, then the transformation T is called a nilrotation, and
$T(g\Gamma )=(bg)\Gamma $
, then the transformation T is called a nilrotation, and
![]() $(X,m_X, T)$
is called a nilsystem. If the transformation T is ergodic, we say that b acts ergodically on the nilmanifold X. It can be proven that b acts ergodically on X if and only if the sequence
$(X,m_X, T)$
is called a nilsystem. If the transformation T is ergodic, we say that b acts ergodically on the nilmanifold X. It can be proven that b acts ergodically on X if and only if the sequence
![]() $(b^nx)_{n\in \mathbb {N}}$
is dense on X for all
$(b^nx)_{n\in \mathbb {N}}$
is dense on X for all
![]() $x\in X$
(see, for instance, [Reference Host and Kra12, Ch. 11]).
$x\in X$
(see, for instance, [Reference Host and Kra12, Ch. 11]).
Let
![]() $x_n$
be a sequence of elements on
$x_n$
be a sequence of elements on
![]() $X=G/\Gamma $
. We say that
$X=G/\Gamma $
. We say that
![]() $x_n$
is equidistributed on
$x_n$
is equidistributed on
![]() $X=G/\Gamma $
if and only if for every continuous function
$X=G/\Gamma $
if and only if for every continuous function
![]() $F:X\to \mathbb {C}$
, we have
$F:X\to \mathbb {C}$
, we have
where
![]() $m_X$
is the (normalized) Haar measure of X.
$m_X$
is the (normalized) Haar measure of X.
A rational subgroup H is a subgroup of
![]() $G $
such that
$G $
such that
![]() $H\cdot e_X$
is a closed subset of
$H\cdot e_X$
is a closed subset of
![]() $X=G/\Gamma $
, where
$X=G/\Gamma $
, where
![]() $e_X$
is the identity element of X. Equivalently,
$e_X$
is the identity element of X. Equivalently,
![]() $H\Gamma $
is a closed subset of the space G. This also implies that H must be closed in G (see [Reference Host and Kra12, Ch. 10, Lemma 14]). A subnilmanifold of X is a set
$H\Gamma $
is a closed subset of the space G. This also implies that H must be closed in G (see [Reference Host and Kra12, Ch. 10, Lemma 14]). A subnilmanifold of X is a set
![]() $Y\subset X$
of the form
$Y\subset X$
of the form
![]() $H\cdot x$
, where x is an element of X and H is a rational subgroup of G.
$H\cdot x$
, where x is an element of X and H is a rational subgroup of G.
B.1.1 Horizontal torus and characters
Assume
![]() $X=G/\Gamma $
is a k-step nilmanifold with G connected and simply connected and consider the subgroup
$X=G/\Gamma $
is a k-step nilmanifold with G connected and simply connected and consider the subgroup
![]() $G_2=[G,G]$
. The nilmanifold
$G_2=[G,G]$
. The nilmanifold
![]() $Z=G/(G_2\Gamma )$
is called the horizontal torus of X. We observe that Z is a connected, compact Abelian Lie group, and thus isomorphic to some torus
$Z=G/(G_2\Gamma )$
is called the horizontal torus of X. We observe that Z is a connected, compact Abelian Lie group, and thus isomorphic to some torus
![]() $\mathbb {T}^{d}$
. For a
$\mathbb {T}^{d}$
. For a
![]() $b\in G$
, it can be shown that the nilrotation induced by b is ergodic if and only if the induced action of b on Z is ergodic [Reference Parry15, Theorem 3] (see also the theorem in [Reference Leibman13, §2.17]).
$b\in G$
, it can be shown that the nilrotation induced by b is ergodic if and only if the induced action of b on Z is ergodic [Reference Parry15, Theorem 3] (see also the theorem in [Reference Leibman13, §2.17]).
A horizontal character
![]() $\chi $
is a continuous group morphism
$\chi $
is a continuous group morphism
![]() $\chi :G\to \mathbb {C}$
, such that
$\chi :G\to \mathbb {C}$
, such that
![]() $\chi (g\gamma )=\chi (g)$
for all
$\chi (g\gamma )=\chi (g)$
for all
![]() $\gamma \in \Gamma $
. We observe that
$\gamma \in \Gamma $
. We observe that
![]() $\chi $
also annihilates
$\chi $
also annihilates
![]() $G_2$
and therefore descends to the horizontal torus Z. Thus, under the natural projection map
$G_2$
and therefore descends to the horizontal torus Z. Thus, under the natural projection map
![]() $\pi $
,
$\pi $
,
![]() $\chi $
becomes a character on some torus
$\chi $
becomes a character on some torus
![]() $\mathbb {T}^d$
. We will often use the notation
$\mathbb {T}^d$
. We will often use the notation
![]() $\chi \circ \pi $
when working in the horizontal torus, while we reserve the letter
$\chi \circ \pi $
when working in the horizontal torus, while we reserve the letter
![]() $\chi $
to denote the same character in the original group G.
$\chi $
to denote the same character in the original group G.
B.1.2 Change of base point
For every
![]() $b\in G$
, we have that the sequence
$b\in G$
, we have that the sequence
![]() $b^n\Gamma $
is equidistributed in the set
$b^n\Gamma $
is equidistributed in the set
![]() $ \{\overline {b^n\Gamma \colon n\in \mathbb {Z}}\}$
. Therefore, if g is any other element in G, we have that the sequence
$ \{\overline {b^n\Gamma \colon n\in \mathbb {Z}}\}$
. Therefore, if g is any other element in G, we have that the sequence
![]() $b^ng\Gamma $
is equidistributed in the nilmanifold
$b^ng\Gamma $
is equidistributed in the nilmanifold
![]() $g\overline {\{(g^{-1}bg )^n\Gamma ,n\in \mathbb {N}\}}$
. This follows by noting that
$g\overline {\{(g^{-1}bg )^n\Gamma ,n\in \mathbb {N}\}}$
. This follows by noting that
![]() $b^ng=g(g^{-1}bg)^n$
. An analogous relation holds for the elements of the set
$b^ng=g(g^{-1}bg)^n$
. An analogous relation holds for the elements of the set
![]() $(b^sg)_{s\in \mathbb {R}}$
, which we define below. This trick, which is called the change of base point trick, can be used when we want to show that some sequence
$(b^sg)_{s\in \mathbb {R}}$
, which we define below. This trick, which is called the change of base point trick, can be used when we want to show that some sequence
![]() $v(n)x$
is equidistributed (on some specific nilmanifold depending on x) to change the base point x to
$v(n)x$
is equidistributed (on some specific nilmanifold depending on x) to change the base point x to
![]() $\Gamma $
.
$\Gamma $
.
B.1.3 Reduction to connected–simply connected Lie groups
Let G be a k-step nilpotent Lie group and let
![]() $\Gamma $
be a uniform subgroup of G. Then, the space
$\Gamma $
be a uniform subgroup of G. Then, the space
![]() $X=G/\Gamma $
is called a k-step nilmanifold. The space X may have several representations of the form
$X=G/\Gamma $
is called a k-step nilmanifold. The space X may have several representations of the form
![]() $G/\Gamma $
(with possible variance in the degree of nilpotency). Let
$G/\Gamma $
(with possible variance in the degree of nilpotency). Let
![]() $G^{\circ }$
be the connected component of
$G^{\circ }$
be the connected component of
![]() $e_G$
in G. If we assume that
$e_G$
in G. If we assume that
![]() $G/G^{\circ }$
is finitely generated (without loss of generality, we can assume that in this article, because our results deal with the action of G on finitely many elements of X), then by passing to the universal cover
$G/G^{\circ }$
is finitely generated (without loss of generality, we can assume that in this article, because our results deal with the action of G on finitely many elements of X), then by passing to the universal cover
![]() $\tilde {G}$
of G, it can be shown that X has a representation
$\tilde {G}$
of G, it can be shown that X has a representation
![]() $\tilde {G}/\tilde {\Gamma }$
where now the underlying group
$\tilde {G}/\tilde {\Gamma }$
where now the underlying group
![]() $\tilde {G}$
is simply connected. In addition, we can argue as in [Reference Leibman13, §1.11] to deduce that X can be embedded as a subnilmanifold in some nilmanifold
$\tilde {G}$
is simply connected. In addition, we can argue as in [Reference Leibman13, §1.11] to deduce that X can be embedded as a subnilmanifold in some nilmanifold
![]() $G'/\Gamma '$
, where
$G'/\Gamma '$
, where
![]() $G'$
is a connected and simply connected nilpotent Lie group and every translation on X has a representation in
$G'$
is a connected and simply connected nilpotent Lie group and every translation on X has a representation in
![]() $X'=G'/\Gamma '$
. This means that for any
$X'=G'/\Gamma '$
. This means that for any
![]() $x\in X,\ b_1,\ldots b_k\in G$
and continuous function
$x\in X,\ b_1,\ldots b_k\in G$
and continuous function
![]() $F:X\to \mathbb {C}$
, we can find
$F:X\to \mathbb {C}$
, we can find
![]() $x'\in X'$
,
$x'\in X'$
,
![]() $b_1',\ldots ,b^{\prime }_k\in G'$
and
$b_1',\ldots ,b^{\prime }_k\in G'$
and
![]() $F':X'\to \mathbb {C}$
, such that
$F':X'\to \mathbb {C}$
, such that
![]() $F(b_1^{n_1}\cdots b_k^{n_k}x)= F'((b_1')^{n_1}\cdots (b^{\prime }_k)^{n_k}x)$
for all
$F(b_1^{n_1}\cdots b_k^{n_k}x)= F'((b_1')^{n_1}\cdots (b^{\prime }_k)^{n_k}x)$
for all
![]() $n_1,\ldots ,n_k\in \mathbb {Z}$
.
$n_1,\ldots ,n_k\in \mathbb {Z}$
.
B.2 Nilorbits and Ratner’s theorem
Let G be a connected and simply connected Lie group. It is well known that the exponential map
![]() $\exp $
from the Lie algebra of G to G is a diffeomorphism. In particular, it is a bijection between G and its Lie algebra
$\exp $
from the Lie algebra of G to G is a diffeomorphism. In particular, it is a bijection between G and its Lie algebra
![]() $\mathfrak {g}$
. For
$\mathfrak {g}$
. For
![]() $b\in G$
and
$b\in G$
and
![]() $t\in \mathbb {R}$
, we can then define the element
$t\in \mathbb {R}$
, we can then define the element
![]() $b^t$
as the unique element of G satisfying
$b^t$
as the unique element of G satisfying
![]() $b^t=\exp (tX)$
, where
$b^t=\exp (tX)$
, where
![]() $\exp (X)=b$
. As a corollary of Ratner’s theorem [Reference Ratner16], we get the following lemma.
$\exp (X)=b$
. As a corollary of Ratner’s theorem [Reference Ratner16], we get the following lemma.
Lemma B.1. Let
![]() $G/\Gamma $
be a nilmanifold with G connected and simply connected. For any elements
$G/\Gamma $
be a nilmanifold with G connected and simply connected. For any elements
![]() $b_1,\ldots ,b_k\in \Gamma $
, we have that the set
$b_1,\ldots ,b_k\in \Gamma $
, we have that the set
is a subnilmanifold of X with a representation
![]() $H/\Delta $
for some closed, connected and rational subgroup H of G that contains the elements
$H/\Delta $
for some closed, connected and rational subgroup H of G that contains the elements
![]() $b_1^s,\ldots ,b_k^s$
for all
$b_1^s,\ldots ,b_k^s$
for all
![]() $s\in \mathbb {R}$
and
$s\in \mathbb {R}$
and
![]() $\Delta $
is a uniform subgroup of H.
$\Delta $
is a uniform subgroup of H.
We call the set
![]() $\{\overline {b^t\Gamma \colon t\in \mathbb {R}}\}$
the nilorbit of the element b. We will analogously denote by
$\{\overline {b^t\Gamma \colon t\in \mathbb {R}}\}$
the nilorbit of the element b. We will analogously denote by
![]() $\overline {b^{\mathbb {Z}}\Gamma }$
the set
$\overline {b^{\mathbb {Z}}\Gamma }$
the set
![]() $\{\overline {b^n\Gamma \colon n\in \mathbb {Z}}\}$
and
$\{\overline {b^n\Gamma \colon n\in \mathbb {Z}}\}$
and
![]() $\overline {b^{\mathbb {N}}\Gamma }=\{\overline {b^n\Gamma \colon n\in \mathbb {N}}\}$
.
$\overline {b^{\mathbb {N}}\Gamma }=\{\overline {b^n\Gamma \colon n\in \mathbb {N}}\}$
.
We establish the following lemma, which will be necessary for our proofs.
Lemma B.2. Let
![]() $X=G/\Gamma $
be a nilmanifold and let
$X=G/\Gamma $
be a nilmanifold and let
![]() $b_1,\ldots ,b_k\in \Gamma $
be any pairwise commuting elements. Then, there exists a real number t such that
$b_1,\ldots ,b_k\in \Gamma $
be any pairwise commuting elements. Then, there exists a real number t such that
Proof. We want to find some
![]() $t\in \mathbb {R}$
so that the sequence
$t\in \mathbb {R}$
so that the sequence
is equidistributed on the nilmanifold
![]() $Y=\overline {b_1^{\mathbb {R}}\cdots b_k^{\mathbb {R}}\Gamma }$
. By Lemma B.1, Y has a representation as
$Y=\overline {b_1^{\mathbb {R}}\cdots b_k^{\mathbb {R}}\Gamma }$
. By Lemma B.1, Y has a representation as
![]() $H/\Delta $
, where H is connected, simply connected and rational. Observe that
$H/\Delta $
, where H is connected, simply connected and rational. Observe that
![]() $\phi _t$
naturally induces a
$\phi _t$
naturally induces a
![]() $\mathbb {Z}^k$
action on Y by
$\mathbb {Z}^k$
action on Y by
![]() $(\phi _t(n_1,\ldots ,n_k),h\Delta )\to b_1^{n_1t}\cdots b_k^{n_k t}h\Delta $
. It is sufficient to show that this
$(\phi _t(n_1,\ldots ,n_k),h\Delta )\to b_1^{n_1t}\cdots b_k^{n_k t}h\Delta $
. It is sufficient to show that this
![]() $\mathbb {Z}^k$
-action is ergodic on Y, since this implies that
$\mathbb {Z}^k$
-action is ergodic on Y, since this implies that
![]() $Y=\overline {\{\phi _t({\mathbf n})y,{\mathbf n}\in \mathbb {Z}^k\}}$
for all
$Y=\overline {\{\phi _t({\mathbf n})y,{\mathbf n}\in \mathbb {Z}^k\}}$
for all
![]() $y\in Y$
. However, using the results in [Reference Leibman13] (specifically, Theorem 2.17), the above action is ergodic if and only if it is ergodic on the horizontal torus Z of Y, which is homeomorphic to some torus
$y\in Y$
. However, using the results in [Reference Leibman13] (specifically, Theorem 2.17), the above action is ergodic if and only if it is ergodic on the horizontal torus Z of Y, which is homeomorphic to some torus
![]() $\mathbb {T}^d$
. Equivalently, if we denote by
$\mathbb {T}^d$
. Equivalently, if we denote by
![]() $(b_{i,1},\ldots ,b_{i,d})$
the projection of the point
$(b_{i,1},\ldots ,b_{i,d})$
the projection of the point
![]() $b_i\Gamma $
on Z, then we need to check whether the sequence
$b_i\Gamma $
on Z, then we need to check whether the sequence
is dense on
![]() $\mathbb {T}^d$
. It suffices to choose t so that
$\mathbb {T}^d$
. It suffices to choose t so that
![]() $1/t$
is rationally independent of any integer combination of the coordinates
$1/t$
is rationally independent of any integer combination of the coordinates
![]() $b_{i,j}$
. This completes the proof.
$b_{i,j}$
. This completes the proof.
B.3 Polynomial sequences on nilmanifolds
We provide the general definition of polynomial sequences with respect to some filtration.
Definition B.3. A filtration
![]() $G_{\bullet }$
of degree d on a nilpotent Lie group G is a sequence of closed connected subgroups
$G_{\bullet }$
of degree d on a nilpotent Lie group G is a sequence of closed connected subgroups
such that
![]() $[G^{(i)},G^{(j)}]\subseteq G^{(i+j)}$
for all
$[G^{(i)},G^{(j)}]\subseteq G^{(i+j)}$
for all
![]() $i,j\geq 0$
. The filtration is called rational if all groups
$i,j\geq 0$
. The filtration is called rational if all groups
![]() $G^{(i)}$
appearing in the above sequence are rational subgroups of G. A polynomial sequence on G with respect to the above filtration is a sequence
$G^{(i)}$
appearing in the above sequence are rational subgroups of G. A polynomial sequence on G with respect to the above filtration is a sequence
![]() $g(n)$
such that, for all positive integers
$g(n)$
such that, for all positive integers
![]() $h_1,\ldots ,h_k$
, we have that the sequence
$h_1,\ldots ,h_k$
, we have that the sequence
![]() $\partial _{h_1}\cdots \partial _{h_k} g$
takes values in
$\partial _{h_1}\cdots \partial _{h_k} g$
takes values in
![]() $G^{(k)}$
, for all
$G^{(k)}$
, for all
![]() $k\in \mathbb {N}$
, where
$k\in \mathbb {N}$
, where
![]() $\partial _h $
denotes the ‘differencing operator’ that maps the sequence
$\partial _h $
denotes the ‘differencing operator’ that maps the sequence
![]() $(g(n))_{n\in \mathbb {N}}$
to the sequence
$(g(n))_{n\in \mathbb {N}}$
to the sequence
![]() $(g(n+h)(g(n))^{-1})_{n\in \mathbb {N}}$
.
$(g(n+h)(g(n))^{-1})_{n\in \mathbb {N}}$
.
An example of a filtration is the lower central series of the group G. For the purposes of this article, we will only need to consider polynomial sequences of the form
where
![]() $b_i\in G$
for all
$b_i\in G$
for all
![]() $1\leq i\leq k$
and
$1\leq i\leq k$
and
![]() $p_i$
are real polynomials. Note that the terms
$p_i$
are real polynomials. Note that the terms
![]() $b_i^{p_i(n)}$
are well defined, due to our connectedness assumptions. To see that this is indeed a polynomial sequence with our initial definition, we construct a specific filtration on G. We assume that G is k-step nilpotent and we also denote the maximum degree among the polynomials
$b_i^{p_i(n)}$
are well defined, due to our connectedness assumptions. To see that this is indeed a polynomial sequence with our initial definition, we construct a specific filtration on G. We assume that G is k-step nilpotent and we also denote the maximum degree among the polynomials
![]() $p_i$
as d. We consider the filtration (of degree
$p_i$
as d. We consider the filtration (of degree
![]() $dk$
)
$dk$
)
![]() $G_{\bullet }=(G^{(i)})_{0\leq i\leq dk}$
, where
$G_{\bullet }=(G^{(i)})_{0\leq i\leq dk}$
, where
![]() $G^{(i)}=G_{ \left \lfloor {i/d} \right \rfloor +1}$
and
$G^{(i)}=G_{ \left \lfloor {i/d} \right \rfloor +1}$
and
![]() $G_j$
are the commutator subgroups of G. This is a rational filtration because all commutator subgroups of G are rational (see [Reference Host and Kra12, Ch. 10, Proposition 22] for the proof). Then, the sequence
$G_j$
are the commutator subgroups of G. This is a rational filtration because all commutator subgroups of G are rational (see [Reference Host and Kra12, Ch. 10, Proposition 22] for the proof). Then, the sequence
![]() $v(n)$
in equation (B.5) is a polynomial sequence with respect to this filtration. We direct the reader to the discussion after [Reference Green and Tao9, Corollary 6.8], where these last observations were made originally. We will also call the projected sequence
$v(n)$
in equation (B.5) is a polynomial sequence with respect to this filtration. We direct the reader to the discussion after [Reference Green and Tao9, Corollary 6.8], where these last observations were made originally. We will also call the projected sequence
![]() $v(n)\Gamma $
on
$v(n)\Gamma $
on
![]() $X=G/\Gamma $
a polynomial sequence on X.
$X=G/\Gamma $
a polynomial sequence on X.
B.4 Quantitative equidistribution
Assume that
![]() $p(t)$
is a polynomial. Then,
$p(t)$
is a polynomial. Then,
![]() $p(n)$
can be expressed uniquely in the form
$p(n)$
can be expressed uniquely in the form
 $$ \begin{align*} p(n)=\sum_{i=0}^{d}a_i n^i \end{align*} $$
$$ \begin{align*} p(n)=\sum_{i=0}^{d}a_i n^i \end{align*} $$
for some real numbers
![]() $a_i$
and
$a_i$
and
![]() $d\in \mathbb {N}$
. For
$d\in \mathbb {N}$
. For
![]() $N\in \mathbb {N}$
, we define the smoothness norm
$N\in \mathbb {N}$
, we define the smoothness norm
(The definition of the smoothness norms is a bit different in [Reference Green and Tao9]. There, the authors write the polynomials in the form
![]() $p(n)=\sum _{i=0}^{d}a_i\binom {n}{i}$
and define the smoothness norm using the same definition as equation (B.6) (the coefficients
$p(n)=\sum _{i=0}^{d}a_i\binom {n}{i}$
and define the smoothness norm using the same definition as equation (B.6) (the coefficients
![]() $a_i$
are different). However, these definitions give two equivalent norms and, thus, all theorems can be stated for both norms, up to changes in the absolute constants.)
$a_i$
are different). However, these definitions give two equivalent norms and, thus, all theorems can be stated for both norms, up to changes in the absolute constants.)
A filtration on a Lie group G gives rise to a basis on its Lie algebra
![]() $\mathcal {B}$
, which is called a Mal’cev basis [Reference Mal’cev14]. Mal’cev bases play an essential role in the theory of quantitative equidistribution on nilmanifolds. First, we give the following definition.
$\mathcal {B}$
, which is called a Mal’cev basis [Reference Mal’cev14]. Mal’cev bases play an essential role in the theory of quantitative equidistribution on nilmanifolds. First, we give the following definition.
Definition B.4. Let
![]() $X=G/\Gamma $
be a k-step nilmanifold with a rational filtration
$X=G/\Gamma $
be a k-step nilmanifold with a rational filtration
![]() $G_{\bullet }=(G^{(i)})_{i\geq 0}$
. Define
$G_{\bullet }=(G^{(i)})_{i\geq 0}$
. Define
![]() $m=\text {dim}(G)$
and
$m=\text {dim}(G)$
and
![]() $m_i=\text {dim}(G^{(i)})$
. A basis
$m_i=\text {dim}(G^{(i)})$
. A basis
![]() $(\xi _1,\ldots ,\xi _m)$
of the associated Lie algebra
$(\xi _1,\ldots ,\xi _m)$
of the associated Lie algebra
![]() $\mathfrak {g}$
over
$\mathfrak {g}$
over
![]() $\mathbb {R}$
is called a Mal’cev basis adapted to
$\mathbb {R}$
is called a Mal’cev basis adapted to
![]() $G_{\bullet }$
, if the following conditions are met.
$G_{\bullet }$
, if the following conditions are met.
-
(i) For each
 $0\leq j\leq m-1$
,
$0\leq j\leq m-1$
,
 $\mathfrak {h}_j=\textit {span}(\xi _{h+1},\ldots ,\xi _m)$
is a Lie algebra ideal on
$\mathfrak {h}_j=\textit {span}(\xi _{h+1},\ldots ,\xi _m)$
is a Lie algebra ideal on
 $\mathfrak {g}$
and thus
$\mathfrak {g}$
and thus
 $H_j=\exp (\mathfrak {h}_j)$
is a normal Lie subgroup of G.
$H_j=\exp (\mathfrak {h}_j)$
is a normal Lie subgroup of G. -
(ii) For every
 $0\leq i\leq k$
, we have
$0\leq i\leq k$
, we have
 $G^{(i)}=H_{m-m_i}$
.
$G^{(i)}=H_{m-m_i}$
. -
(iii) Each
 $b\in G$
can be uniquely written in the form
$b\in G$
can be uniquely written in the form
 $\exp (t_1\xi _1)\cdots \exp (t_m\xi _m)$
for
$\exp (t_1\xi _1)\cdots \exp (t_m\xi _m)$
for
 $t_i\in \mathbb {R}$
.
$t_i\in \mathbb {R}$
. -
(iv) The subgroup
 $\Gamma $
consists precisely of those elements which, when written in the above form, have all
$\Gamma $
consists precisely of those elements which, when written in the above form, have all
 $t_i\in \mathbb {Z}$
.
$t_i\in \mathbb {Z}$
.
Suppose that the element b is written in the form
![]() $\exp (t_1\xi _1)\cdots \exp (t_m\xi _m)$
. The map
$\exp (t_1\xi _1)\cdots \exp (t_m\xi _m)$
. The map
![]() $\psi :G\to \mathbb {R}^m $
defined by
$\psi :G\to \mathbb {R}^m $
defined by
![]() $\psi (b)= (t_1,\ldots ,t_m)$
is a diffeomorphism from G to
$\psi (b)= (t_1,\ldots ,t_m)$
is a diffeomorphism from G to
![]() $\mathbb {R}^m$
. The numbers
$\mathbb {R}^m$
. The numbers
![]() $(t_1,\ldots ,t_m)$
are called the coordinates of g with respect to the associated Mal’cev basis. If we consider the Euclidean metric on
$(t_1,\ldots ,t_m)$
are called the coordinates of g with respect to the associated Mal’cev basis. If we consider the Euclidean metric on
![]() $\mathbb {R}^m$
, we can construct a Riemannian metric
$\mathbb {R}^m$
, we can construct a Riemannian metric
![]() $d_G$
on G, whose value at the origin is equal to the Euclidean metric of
$d_G$
on G, whose value at the origin is equal to the Euclidean metric of
![]() $\mathbb {R}^m$
at the origin (of
$\mathbb {R}^m$
at the origin (of
![]() $\mathbb {R}^{m}$
) composed with the inverse map
$\mathbb {R}^{m}$
) composed with the inverse map
![]() $\psi ^{-1}$
. This metric is invariant under right translations and induces a metric
$\psi ^{-1}$
. This metric is invariant under right translations and induces a metric
![]() $d_X$
on
$d_X$
on
![]() $X=G/\Gamma $
defined by the relation:
$X=G/\Gamma $
defined by the relation:
The metric used in [Reference Green and Tao9] is slightly different than the one we consider here, but as the authors remark, these metrics are equivalent and all theorems hold as well by changing the absolute constants.
The sequence
![]() $(g(n)\Gamma )_{1\leq n\leq N}$
is said to be
$(g(n)\Gamma )_{1\leq n\leq N}$
is said to be
![]() $\delta $
-equidistributed on the nilmanifold
$\delta $
-equidistributed on the nilmanifold
![]() $X=G/\Gamma $
if and only if for any Lipschitz function
$X=G/\Gamma $
if and only if for any Lipschitz function
![]() $F:X\to \mathbb {C}$
, we have that
$F:X\to \mathbb {C}$
, we have that
 $$ \begin{align*} \bigg| \underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} F(g(n)\Gamma) -\int_X Fd\mu_X \bigg|\leq \delta \lVert F \rVert_{\text{Lip}(X)}, \end{align*} $$
$$ \begin{align*} \bigg| \underset{1\leq n\leq N}{\operatorname*{\mathrm{\mathbb{E}}}} F(g(n)\Gamma) -\int_X Fd\mu_X \bigg|\leq \delta \lVert F \rVert_{\text{Lip}(X)}, \end{align*} $$
where
 $$ \begin{align*} \lVert F \rVert_{\text{Lip}(X)}=\lVert F \rVert_{\infty} +\sup_{x,y\in X,\ x\neq y}^{}\frac{|F(x)-F(y)|}{d_X(x,y)}. \end{align*} $$
$$ \begin{align*} \lVert F \rVert_{\text{Lip}(X)}=\lVert F \rVert_{\infty} +\sup_{x,y\in X,\ x\neq y}^{}\frac{|F(x)-F(y)|}{d_X(x,y)}. \end{align*} $$
We now fix a k-step nilmanifold
![]() $X=G/\Gamma $
, as well as a positive integer d. We equip it with the rational filtration
$X=G/\Gamma $
, as well as a positive integer d. We equip it with the rational filtration
![]() $G_{\bullet }$
of degree
$G_{\bullet }$
of degree
![]() $dk$
that we defined above (after Definition B.3), as well as a Mal’cev basis adapted to this filtration and the corresponding coordinate map
$dk$
that we defined above (after Definition B.3), as well as a Mal’cev basis adapted to this filtration and the corresponding coordinate map
![]() $\psi : G\to \mathbb {R}^m$
(m is the dimension of G). Observe that under this filtration, we have that
$\psi : G\to \mathbb {R}^m$
(m is the dimension of G). Observe that under this filtration, we have that
![]() $G^{(d+1)}=G_2$
and property (ii) in Definition B.4 implies that
$G^{(d+1)}=G_2$
and property (ii) in Definition B.4 implies that
![]() $G_2=H_{m-m_{d+1}}$
. Thus, the Mal’cev basis induces an isometric identification of the horizontal torus
$G_2=H_{m-m_{d+1}}$
. Thus, the Mal’cev basis induces an isometric identification of the horizontal torus
![]() $Z=G/G_2\Gamma $
with the torus
$Z=G/G_2\Gamma $
with the torus
![]() $\mathbb {T}^{m-m_{d+1}}$
equipped with the standard metric.
$\mathbb {T}^{m-m_{d+1}}$
equipped with the standard metric.
Let
![]() $\pi : X\to Z$
denote the projection map and let
$\pi : X\to Z$
denote the projection map and let
![]() $\chi $
be a horizontal character on G. Consider an element
$\chi $
be a horizontal character on G. Consider an element
![]() $b\in G$
with coordinates
$b\in G$
with coordinates
![]() $(t_1,\ldots ,t_m)$
. Then, by properties (iii) and (iv) in Definition B.4, we have that there is some
$(t_1,\ldots ,t_m)$
. Then, by properties (iii) and (iv) in Definition B.4, we have that there is some
![]() $ \overset {\rightarrow }{\ell }=(\ell _1,\ldots ,\ell _{m-m_{d+1}})\in \mathbb {Z}^{m-m_{d+1}}$
such that
$ \overset {\rightarrow }{\ell }=(\ell _1,\ldots ,\ell _{m-m_{d+1}})\in \mathbb {Z}^{m-m_{d+1}}$
such that
Thus, we get a character on the torus
![]() $\mathbb {T}^{m-m_{d+1}}$
(written here with additive notation). We can then define the modulus
$\mathbb {T}^{m-m_{d+1}}$
(written here with additive notation). We can then define the modulus
![]() $\lVert \chi \rVert $
of the character
$\lVert \chi \rVert $
of the character
![]() $\chi $
to be equal to
$\chi $
to be equal to
If
![]() $v(n)$
is the polynomial sequence in equation (B.5) (recall that it is a polynomial sequence with respect to the filtration
$v(n)$
is the polynomial sequence in equation (B.5) (recall that it is a polynomial sequence with respect to the filtration
![]() $G_{\bullet }$
), then the sequence
$G_{\bullet }$
), then the sequence
![]() $\chi \circ \pi (v(n)\Gamma )$
is a polynomial sequence on the horizontal torus
$\chi \circ \pi (v(n)\Gamma )$
is a polynomial sequence on the horizontal torus
![]() $Z\cong \mathbb {T}^{m-m_{d+1}}$
. Indeed, if we denote
$Z\cong \mathbb {T}^{m-m_{d+1}}$
. Indeed, if we denote
![]() $\psi (b_i)=(t_{i,1},\ldots ,t_{i,m})$
, then a simple calculation shows that
$\psi (b_i)=(t_{i,1},\ldots ,t_{i,m})$
, then a simple calculation shows that
 $$ \begin{align*} \chi(\pi(v(n)\Gamma))&=\chi(\pi(b_1^{p_1(n)}\cdot \cdots\cdot b_k^{p_k(n)}))\\&=p_1(n)(\ell_1 t_{1,1}+\cdots+\ell_{m-m_{d+1}}t_{1,m-m_{d+1}})\\&\quad+\cdots +p_k(n)(\ell_1 t_{k,1}+\cdots+\ell_{m-m_{d+1}}t_{k,m-m_{d+1}}), \end{align*} $$
$$ \begin{align*} \chi(\pi(v(n)\Gamma))&=\chi(\pi(b_1^{p_1(n)}\cdot \cdots\cdot b_k^{p_k(n)}))\\&=p_1(n)(\ell_1 t_{1,1}+\cdots+\ell_{m-m_{d+1}}t_{1,m-m_{d+1}})\\&\quad+\cdots +p_k(n)(\ell_1 t_{k,1}+\cdots+\ell_{m-m_{d+1}}t_{k,m-m_{d+1}}), \end{align*} $$
which makes the fact that
![]() $\chi (\pi (v(n)\Gamma ))$
is a polynomial sequence more evident.
$\chi (\pi (v(n)\Gamma ))$
is a polynomial sequence more evident.
The primary tool that we shall use is the following theorem of Green and Tao which describes the orbits of polynomial sequences in finite intervals. We present it in the case of our filtration
![]() $G_{\bullet }$
, although the statement holds for any rational filtration. Some quantitative information (specifically relating to the concepts of quantitative rationality of Mal’cev bases) has been suppressed, since in our applications, the nilmanifold will be fixed and the above condition on the Mal’cev bases is guaranteed if we take
$G_{\bullet }$
, although the statement holds for any rational filtration. Some quantitative information (specifically relating to the concepts of quantitative rationality of Mal’cev bases) has been suppressed, since in our applications, the nilmanifold will be fixed and the above condition on the Mal’cev bases is guaranteed if we take
![]() $\delta $
small enough.
$\delta $
small enough.
Theorem F. [Reference Green and Tao9, Theorem 2.9]
Let d be a non-negative integer,
![]() $X=G/\Gamma $
be a nilmanifold with G connected and simply connected, and we equip the nilmanifold X with the Mal’cev basis adapted to the
$X=G/\Gamma $
be a nilmanifold with G connected and simply connected, and we equip the nilmanifold X with the Mal’cev basis adapted to the
![]() $dk$
filtration
$dk$
filtration
![]() $G_{\bullet }$
as above. Assume
$G_{\bullet }$
as above. Assume
![]() $\delta $
is a sufficiently small (depending only on
$\delta $
is a sufficiently small (depending only on
![]() $X,d$
) parameter. Then, there exist a positive constant
$X,d$
) parameter. Then, there exist a positive constant
![]() $C=C(X,d)$
with the following property: for every
$C=C(X,d)$
with the following property: for every
![]() $N\in \mathbb {N}$
, if
$N\in \mathbb {N}$
, if
![]() $(v(n))_{n\in \mathbb {N}} $
is a polynomial sequence with respect to
$(v(n))_{n\in \mathbb {N}} $
is a polynomial sequence with respect to
![]() $G_{\bullet }$
such that the finite sequence
$G_{\bullet }$
such that the finite sequence
![]() $(v(n)\Gamma )_{1\leq n\leq N}$
is not
$(v(n)\Gamma )_{1\leq n\leq N}$
is not
![]() $\delta $
-equidistributed, then for some non-trivial horizontal character
$\delta $
-equidistributed, then for some non-trivial horizontal character
![]() $\chi $
(that depends on N and the sequence
$\chi $
(that depends on N and the sequence
![]() $v(n)$
) of modulus
$v(n)$
) of modulus
![]() $\lVert \chi \rVert \leq \delta ^{-C}$
, we have
$\lVert \chi \rVert \leq \delta ^{-C}$
, we have
where
![]() $\pi $
denotes the projection map from X to its horizontal torus.
$\pi $
denotes the projection map from X to its horizontal torus.
To get a sense of how this theorem works, let us consider an application on a polynomial sequence on
![]() $\mathbb {T}$
. Let d be a positive integer and
$\mathbb {T}$
. Let d be a positive integer and
![]() $\delta>0$
a small real number. Then, there exists a constant C that depends only on d, such that for any polynomial
$\delta>0$
a small real number. Then, there exists a constant C that depends only on d, such that for any polynomial
of degree d, we have either that
or there exists an integer q with
![]() $|q|\leq \delta ^{-C}$
, such that
$|q|\leq \delta ^{-C}$
, such that
for every
![]() $1\leq k\leq d$
. Thus, either the exponential sums of the polynomial sequence
$1\leq k\leq d$
. Thus, either the exponential sums of the polynomial sequence
![]() $p(n)$
are small or the non-constant coefficients
$p(n)$
are small or the non-constant coefficients
![]() $a_k$
satisfy a ‘major-arc’ condition (they are ‘close’ to a rational with denominator bounded by
$a_k$
satisfy a ‘major-arc’ condition (they are ‘close’ to a rational with denominator bounded by
![]() $\delta ^{-C}$
). Observe that the constant C does not depend on the length of the interval N.
$\delta ^{-C}$
). Observe that the constant C does not depend on the length of the interval N.