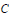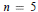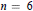17 results
A Remark on the Dixmier Conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 30 August 2019, pp. 6-12
- Print publication:
- March 2020
-
- Article
- Export citation
PRIME SPECTRA OF AMBISKEW POLYNOMIAL RINGS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 16 April 2018, pp. 49-68
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation
Corrigendum to Example in “Quantum Drinfeld Hecke Algebras“
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 4 / 01 August 2014
- Published online by Cambridge University Press:
- 20 November 2018, p. 902
- Print publication:
- 01 August 2014
-
- Article
-
- You have access
- Export citation
Quantum Drinfeld Hecke Algebras
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 4 / 01 August 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 874-901
- Print publication:
- 01 August 2014
-
- Article
-
- You have access
- Export citation
AUTOMORPHISMS OF QUANTUM MATRICES
-
- Journal:
- Glasgow Mathematical Journal / Volume 55 / Issue A / October 2013
- Published online by Cambridge University Press:
- 01 October 2013, pp. 89-100
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
On Automorphisms and Commutativity in Semiprime Rings
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 3 / 01 September 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 584-592
- Print publication:
- 01 September 2013
-
- Article
-
- You have access
- Export citation
RING ENDOMORPHISMS WITH LARGE IMAGES
-
- Journal:
- Glasgow Mathematical Journal / Volume 55 / Issue 2 / May 2013
- Published online by Cambridge University Press:
- 25 February 2013, pp. 381-390
- Print publication:
- May 2013
-
- Article
-
- You have access
- Export citation
EXTENSIONS OF McCOY'S THEOREM
-
- Journal:
- Glasgow Mathematical Journal / Volume 52 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 04 December 2009, pp. 155-159
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation
Group Actions on Quasi-Baer Rings
-
- Journal:
- Canadian Mathematical Bulletin / Volume 52 / Issue 4 / 01 December 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 564-582
- Print publication:
- 01 December 2009
-
- Article
-
- You have access
- Export citation
THE GROUP OF AUTOMORPHISMS OF THE FIRST WEYL ALGEBRA IN PRIME CHARACTERISTIC AND THE RESTRICTION MAP
-
- Journal:
- Glasgow Mathematical Journal / Volume 51 / Issue 2 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 263-274
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
FACTORIZATION OF MONOMORPHISMS OF A POLYNOMIAL ALGEBRA IN ONE VARIABLE
-
- Journal:
- Glasgow Mathematical Journal / Volume 50 / Issue 2 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 191-201
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
THE UNIT SUM NUMBER OF SOME PROJECTIVE MODULES
-
- Journal:
- Glasgow Mathematical Journal / Volume 50 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 71-74
- Print publication:
- January 2008
-
- Article
-
- You have access
- Export citation
On Maps Preserving Products
-
- Journal:
- Canadian Mathematical Bulletin / Volume 48 / Issue 3 / 01 September 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 355-369
- Print publication:
- 01 September 2005
-
- Article
-
- You have access
- Export citation
Dependent Automorphisms in Prime Rings
-
- Journal:
- Canadian Mathematical Bulletin / Volume 41 / Issue 4 / 01 December 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 452-462
- Print publication:
- 01 December 1998
-
- Article
-
- You have access
- Export citation
On certain pairs of automorphisms of rings, II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 2 / April 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 162-168
- Print publication:
- April 1998
-
- Article
-
- You have access
- Export citation
Rings With Finite Maximal Invariant Subrings
-
- Journal:
- Canadian Journal of Mathematics / Volume 48 / Issue 3 / 01 June 1996
- Published online by Cambridge University Press:
- 20 November 2018, pp. 596-606
- Print publication:
- 01 June 1996
-
- Article
-
- You have access
- Export citation
On Commutativity and Strong Commutativity-Preserving Maps
-
- Journal:
- Canadian Mathematical Bulletin / Volume 37 / Issue 4 / 01 December 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 443-447
- Print publication:
- 01 December 1994
-
- Article
-
- You have access
- Export citation



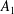
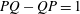
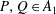
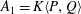
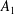
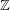
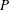
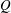
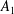
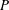
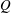
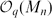

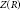
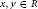
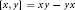



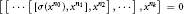
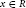
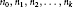
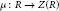
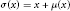

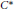
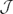
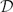

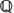 -algebra
-algebra 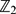 is not a factor of
is not a factor of