Hostname: page-component-77c89778f8-9q27g Total loading time: 0 Render date: 2024-07-17T14:06:56.228Z Has data issue: false hasContentIssue false
  • English
  • Français

On Automorphisms and Commutativity in Semiprime Rings

Published online by Cambridge University Press:  20 November 2018

Pao-Kuei Liau  and
Cheng-Kai Liu
Pao-Kuei Liau
Affiliation:
Department of Mathematics, National Changhua University of Education, Changhua 500, Taiwan e-mail: d96211001@mail.ncue.edu.tw; ckliu@cc.ncue.edu.tw
Cheng-Kai Liu
Affiliation:
Department of Mathematics, National Changhua University of Education, Changhua 500, Taiwan e-mail: d96211001@mail.ncue.edu.tw; ckliu@cc.ncue.edu.tw
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $R$ be a semiprime ring with center 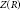$Z\left( R \right)$. For 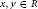$x,\,y\,\in \,R$, we denote by 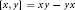$\left[ x,\,y \right]\,=\,xy\,-\,yx$ the commutator of $x$ and $y$. If $\sigma $ is a non-identity automorphism of $R$ such that

1

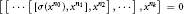$$\left[ \left[ \cdot \cdot \cdot \,\left[ \left[ \sigma \left( {{x}^{n0}} \right),\,{{x}^{n1}} \right],\,{{x}^{n2}} \right],\cdot \cdot \cdot \right],\,{{x}^{nk}} \right]\,=\,0$$

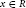for all $x\,\in \,R$, where 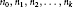${{n}_{0}},\,{{n}_{1}},\,{{n}_{2}},\,...,\,{{n}_{k}}$ are fixed positive integers, then there exists a map 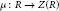$\mu \,:\,R\,\to \,Z\left( R \right)$ such that 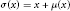$\sigma \left( x \right)\,=\,x\,+\,\mu \left( x \right)$ for all 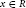$x\,\in \,R$. In particular, when $R$ is a prime ring, $R$ is commutative.

Keywords

16N6016W2016R50semiprime ringautomorphismgeneralized polynomial identity (GPI)
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 3 , 01 September 2013 , pp. 584 - 592
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Albas, E., Argac, N., and De Filippis, V., Generalized derivations with Engel conditions on one-sided ideals. Comm. Algebra 36 (2008), no. 6, 2063–2071. http://dx.doi.org/10.1080/00927870801949328 Google Scholar
[2] Beidar, K. I.,Martindale, W. S. III, and Mikhalev, A. V., Rings with generalized identities. Monographs and Textbooks in Pure and Applied Mathematics, 196, Marcel Dekker, Inc., New York, 1996.Google Scholar
[3] Bell, H. E. and Martindale, W. S. III, Centralizing mappings of semiprime rings. Canad. Math. Bull. 30 (1987), no. 1, 92–101. http://dx.doi.org/10.4153/CMB-1987-014-x Google Scholar
[4] Brešar, M., Centralizing mappings and derivations in prime rings. J. Algebra 156 (1993), no. 2, 385–394. http://dx.doi.org/10.1006/jabr.1993.1080 Google Scholar
[5] Brešar, M., Chebotar, M. A., andW. S.Martindale III, Functional Identities. Frontiers in mathematics. Birkh¨auser Verlag, Basel, 2007.Google Scholar
[6] Chou, M.-C. and Liu, C.-K., An Engel condition with skew derivations. Monatsh. Math. 158 (2009), 259-270. http://dx.doi.org/10.1007/s00605-008-0043-5 Google Scholar
[7] Chuang, C.-L., Differential identities with automorphisms and antiautomorphisms. I. J. Algebra 149 (1992), no. 2, 371–404. http://dx.doi.org/10.1016/0021-8693(92)90023-F Google Scholar
[8] Chuang, C.-L., Differential identities with automorphisms and antiautomorphisms. II. J. Algebra 160 (1993), no. 1, 130–171. http://dx.doi.org/10.1006/jabr.1993.1181 Google Scholar
[9] Chuang, C.-L. and Liu, C.-K., Extended Jacobson density theorem for rings with skew derivations. Comm. Algebra 35 (2007), no. 4, 1391–1413. http://dx.doi.org/10.1080/00927870601142207 Google Scholar
[10] Deng, Q. and Bell, H. E., On derivations and commutativity in semiprime rings. Comm. Algebra 23 (1995), no. 10, 3705–3713. http://dx.doi.org/10.1080/00927879508825427 Google Scholar
[11] Divinsky, N., On commuting automorphisms of rings. Trans. Roy. Soc. Canada. Sect. III. 49 (1955), 19–22.Google Scholar
[12] Erickson, T. S., Martindale, W. S. III, and Osborn, J. M., Prime nonassociative algebras. Pacific J. Math. 60 (1975), 49–63.Google Scholar
[13] De Filippis, V., An Engel condition with generalized derivations on multilinear polynomials. Israel J. Math. 162 (2007), 93–108. http://dx.doi.org/10.1007/s11856-007-0090-y Google Scholar
[14] De Filippis, V., Generalized derivations with Engel condition on multilinear polynomials. Israel J. Math. 171 (2009), 325–348. http://dx.doi.org/10.1007/s11856-009-0052-7 Google Scholar
[15] Jacobson, N., Lie algebras. Interscience Tracts in Pure and Applied Mathematics, 10, Interscience Publishers, New York, 1962.Google Scholar
[16] Jacobson, N., Structure of rings. American Mathematical Society Colloquium Publications, 37, American Mathematical Society, Providence, RI, 1964.Google Scholar
[17] Lanski, C., An Engel condition with derivation. Proc. Amer. Math. Soc. 118 (1993), no. 3, 731–734. http://dx.doi.org/10.1090/S0002-9939-1993-1132851-9 Google Scholar
[18] Lanski, C., An Engel condition with derivation for left ideals. Proc. Amer. Math. Soc. 125 (1997), no. 2, 339–345. http://dx.doi.org/10.1090/S0002-9939-97-03673-3 Google Scholar
[19] Lee, P.-H. and Wong, T.-L., Derivations cocentralizing Lie ideals. Bull. Inst. Math. Acad. Sinica 23 (1995), no. 1, 1–5.Google Scholar
[20] Lee, P.-H. and YuWang, , Supercentralizing maps in prime superalgebras. Comm. Algebra 37 (2009), 840–854. http://dx.doi.org/10.1080/00927870802271672 Google Scholar
[21] Lee, T.-K., Semiprime rings with hypercentral derivations. Canad. Math. Bull. 38 (1995), no. 4, 445–449. http://dx.doi.org/10.4153/CMB-1995-065-2 Google Scholar
[22] Lee, T.-K. and Wong, T.-L., On certain subgroups of prime rings with automorphisms. Comm. Algebra 30 (2002), no. 10, 4997–5009. http://dx.doi.org/10.1081/AGB-120014681 Google Scholar
[23] Lee, T.-K. and K.-Liu, S., The Skolem-Noether theorem for semiprime rings satisfying a strict identity. Comm. Algebra 35 (2007), no. 6, 1949–1955. http://dx.doi.org/10.1080/00927870701247062 Google Scholar
[24] Lee, T.-K.and Zhou, Y., An identity with generalized derivations. J. Algebra Appl. 9 (2009), no. 3, 307–317. http://dx.doi.org/10.1142/S021949880900331X Google Scholar
[25] Liu, C.-K., Derivations with Engel and annihilator conditions on multilinear polynomials. Comm. Algebra 33 (2005), no. 3, 719–725. http://dx.doi.org/10.1081/AGB-200049880 Google Scholar
[26] Liu, C.-K., Derivations cocentralizing multilinear polynomials on left ideal. Monatsh. Math. 162 (2011), no. 3, 297–311. http://dx.doi.org/10.1007/s00605-009-0179-y Google Scholar
[27] Luh, J., A note on commuting automorphisms of rings. Amer. Math. Monthly 77 (1970), 61–62. http://dx.doi.org/10.2307/2316858 Google Scholar
[28] Martindale, W. S. III, Prime rings satisfying a generalized polynomial identity. J. Algebra 12 (1969), 576–584. http://dx.doi.org/10.1016/0021-8693(69)90029-5 Google Scholar
[29] Mayne, J. H., Centralizing automorphisms of prime rings. Canad. Math. Bull. 19 (1976), no. 1, 113–115. http://dx.doi.org/10.4153/CMB-1976-017-1 Google Scholar
[30] Mayne, J. H., Centralizing automorphisms of Lie ideals in prime rings. Canad. Math. Bull. 35 (1992), no. 4, 510–514. http://dx.doi.org/10.4153/CMB-1992-067-0 Google Scholar
[31] Vukman, J., Commuting and centralizing mappings in prime rings. Proc. Amer. Math. Soc. 109 (1990), no. 1, 47–52. http://dx.doi.org/10.1090/S0002-9939-1990-1007517-3 Google Scholar
[32] YuWang, , A note on Lie automorphisms, subrings, and Lie ideals of prime rings. Comm. Algebra 33 (2005), no. 11, 4057–4062. http://dx.doi.org/10.1080/00927870500261363 Google Scholar
[33] YuWang, , Power-centralizing automorphisms of Lie ideals in prime rings. Comm. Algebra 34 (2006), no. 2, 609–615. http://dx.doi.org/10.1080/00927870500387812 Google Scholar
[34] YuWang, , Annihilator conditions of derivations on multilinear polynomial. Comm. Algebra 39 (2011), no. 1, 237–246. http://dx.doi.org/10.1080/00927870903337992 Google Scholar
[35] Wong, T.-L., On Lie automorphisms, additive subgroups, and Lie ideals of prime rings. Comm. Algebra 31 (2003), 969–979. http://dx.doi.org/10.1081/AGB-120017353 Google Scholar