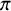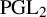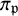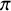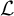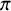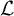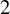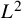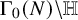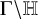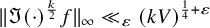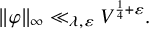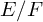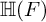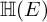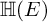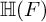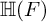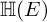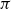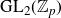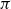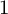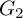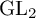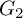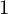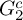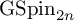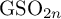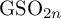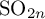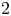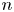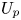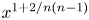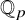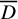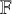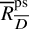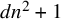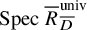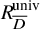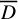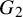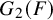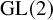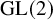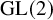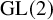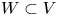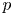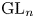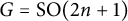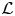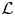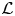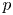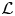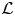143 results
L-invariants for cohomological representations of PGL(2) over arbitrary number fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 30 May 2024, e71
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Theta functions, fourth moments of eigenforms and the sup-norm problem II
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 30 May 2024, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWISTED GAN–GROSS–PRASAD CONJECTURE FOR CERTAIN TEMPERED L-PACKETS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ARCHIMEDEAN NEWFORM THEORY FOR
 $\operatorname {\mathrm {GL}}_n$
$\operatorname {\mathrm {GL}}_n$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 17 May 2024, pp. 1-76
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE DISTINCTION OF IWAHORI-SPHERICAL DISCRETE SERIES REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 17 April 2024, pp. 1-15
-
- Article
-
- You have access
- HTML
- Export citation
Discrepancy of rational points in simple algebraic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 13 March 2024, pp. 836-877
- Print publication:
- April 2024
-
- Article
- Export citation
The sup-norm problem beyond the newform
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 12 March 2024, pp. 517-545
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUNTING DISCRETE, LEVEL-
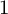 $1$, QUATERNIONIC AUTOMORPHIC REPRESENTATIONS ON
$1$, QUATERNIONIC AUTOMORPHIC REPRESENTATIONS ON 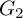 $G_2$
$G_2$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 13 December 2023, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GALOIS REPRESENTATIONS FOR EVEN GENERAL SPECIAL ORTHOGONAL GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 13 December 2023, pp. 1-92
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Slopes in eigenvarieties for definite unitary groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 22 November 2023, pp. 52-89
- Print publication:
- January 2024
-
- Article
- Export citation
Equidimensionality of universal pseudodeformation rings in characteristic p for absolute Galois groups of p-adic fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 17 November 2023, e102
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Local Langlands Conjecture for
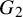 $G_2$
$G_2$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 19 October 2023, e28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exotic Monoidal Structures and Abstractly Automorphic Representations for
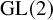 $\mathrm {GL}(2)$
$\mathrm {GL}(2)$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 03 August 2023, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Twisted GGP problems and conjectures
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 31 July 2023, pp. 1916-1973
- Print publication:
- September 2023
-
- Article
- Export citation
On the derived category of the Iwahori–Hecke algebra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 04 May 2023, pp. 1042-1110
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Automorphy lifting with adequate image
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 06 February 2023, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local newforms for the general linear groups over a non-archimedean local field
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 December 2022, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Gelfand–Graev representation of classical groups in terms of Hecke algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 24 June 2022, pp. 1343-1368
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Big principal series,
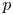 $p$-adic families and
$p$-adic families and 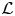 $\mathcal {L}$-invariants
$\mathcal {L}$-invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 25 April 2022, pp. 409-436
- Print publication:
- February 2022
-
- Article
- Export citation
TWISTED DOUBLING INTEGRALS FOR BRYLINSKI–DELIGNE EXTENSIONS OF CLASSICAL GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 01 December 2021, pp. 1931-1985
- Print publication:
- July 2023
-
- Article
- Export citation