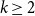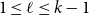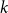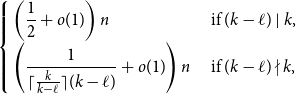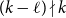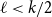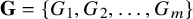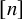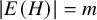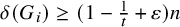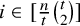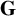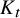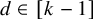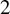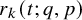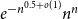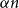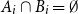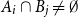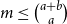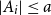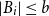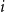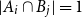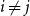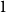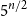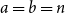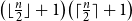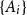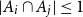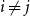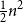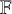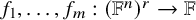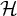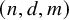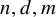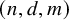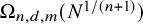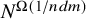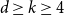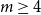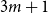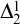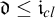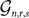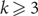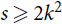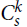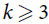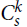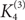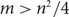51 results
Counting spanning subgraphs in dense hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 30 May 2024, pp. 1-13
-
- Article
- Export citation
Rainbow spanning structures in graph and hypergraph systems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 17 October 2023, e95
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tower Gaps in Multicolour Ramsey Numbers
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 21 September 2023, e84
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the size of maximal intersecting families
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 08 September 2023, pp. 32-49
-
- Article
- Export citation
The codegree Turán density of tight cycles minus one edge
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 05 July 2023, pp. 881-884
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A pair degree condition for Hamiltonian cycles in 3-uniform hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 17 May 2023, pp. 762-781
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Problems and results on 1-cross-intersecting set pair systems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 691-702
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ramsey properties of algebraic graphs and hypergraphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 24 October 2022, e95
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Small non-Leighton two-complexes
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 385-391
- Print publication:
- March 2023
-
- Article
- Export citation
Degree sequences of sufficiently dense random uniform hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 15 August 2022, pp. 183-224
-
- Article
- Export citation
Hypergraphs without non-trivial intersecting subgraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 09 June 2022, pp. 1076-1091
-
- Article
- Export citation
TREE FORCING AND DEFINABLE MAXIMAL INDEPENDENT SETS IN HYPERGRAPHS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 29 April 2022, pp. 1419-1458
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A stochastic matching model on hypergraphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 951-980
- Print publication:
- December 2021
-
- Article
- Export citation
Spanning trees in random regular uniform hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 26 May 2021, pp. 29-53
-
- Article
- Export citation
A proof of a conjecture of Gyárfás, Lehel, Sárközy and Schelp on Berge-cycles
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 09 March 2021, pp. 654-669
-
- Article
- Export citation
Counting Hamilton cycles in Dirac hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 17 December 2020, pp. 631-653
-
- Article
- Export citation
Covering and tiling hypergraphs with tight cycles
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 13 October 2020, pp. 288-329
-
- Article
- Export citation
Tight Hamilton cycles in cherry-quasirandom 3-uniform hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 12 October 2020, pp. 412-443
-
- Article
-
- You have access
- Open access
- Export citation
Finding tight Hamilton cycles in random hypergraphs faster
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 23 September 2020, pp. 239-257
-
- Article
- Export citation
Triangle-degrees in graphs and tetrahedron coverings in 3-graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 09 September 2020, pp. 175-199
-
- Article
-
- You have access
- Open access
- Export citation