Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-05-09T19:48:14.008Z Has data issue: false hasContentIssue false
  • English
  • Français

On the size of maximal intersecting families

Part of: Extremal combinatorics Graph theory

Published online by Cambridge University Press:  08 September 2023

Dmitrii Zakharov
Dmitrii Zakharov*
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA, USA
*
Email: zakhdm@mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that an $n$-uniform maximal intersecting family has size at most 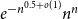$e^{-n^{0.5+o(1)}}n^n$. This improves a recent bound by Frankl ((2019) Comb. Probab. Comput. 28(5) 733–739.). The Spread Lemma of Alweiss et al. ((2020) Proceedings of the 52nd Annual ACM SIGACT Symposium on Theory of Computing.) plays an important role in the proof.

Keywords

Erdos–Lovasz problemintersecting familyminimal covers

MSC classification

Primary: 05D05: Extremal set theory
Secondary: 05C35: Extremal problems 05C65: Hypergraphs 05D15: Transversal (matching) theory
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 33 , Issue 1 , January 2024 , pp. 32 - 49
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alweiss, R., Lovett, S., Wu, K. and Zhang, J. (2020) Improved bounds for the sunflower lemma. In Proceedings of the 52nd Annual ACM SIGACT Symposium on Theory of Computing.Google Scholar
Arman, A. and Retter, T. (2017) An upper bound for the size of a $k$ -uniform intersecting family with covering number $k$ . J. Comb. Theory Ser. A 147 18–26.CrossRefGoogle Scholar
Cherkashin, D. (2011) On hypergraph cliques with chromatic number 3. Moscow J. Comb. Number Theory 1(3) 3–11.Google Scholar
Erdős, P. and Lovász, L. (1973) Problems and results on 3-chromatic hypergraphs and some related questions. Coll. Math. Soc. Janos Bolyai 10. Infin. Finite Sets, Keszthely (Hungary).Google Scholar
Frankl, P. (2017) Antichains of fixed diameter. Mosc. J. Comb. Number Theory 7(3) 3–33.Google Scholar
Frankl, P. (2019) A near-exponential improvement of a bound of Erdős and Lovász on maximal intersecting families. Comb. Prob. Comput. 28(5) 733–739.Google Scholar
Frankl, P., Ota, K. and Tokushige, N. (1996) Covers in uniform intersecting families and a counterexample to a conjecture of Lovász. J. Comb. Theory Ser. A 74(1) 33–42.Google Scholar
Gyárfás, A. (1977) Partition covers and blocking sets in hypergraphs. MTA SZTAKI Tanulmányok 71.Google Scholar
Jukna, S. (2011) Extremal Combinatorics: With Applications in Computer Science. Springer Science & Business Media.Google Scholar
Kahn, J. (1994) On a problem of Erdős and Lovász. II. n(r)=O(r). J. Am. Math. Soc. 7(1) 125–143.Google Scholar
Kupavskii, A. Personal communication.Google Scholar
Rao, A. (2019) Coding for Sunflowers. arXiv preprint arXiv: 1909.04774.Google Scholar
Tao, T. The sunflower lemma via shannon entropy. Available at: https://terrytao.wordpress.com/2020/07/20/the-sunflower-lemma-via-shannon-entropy/.Google Scholar
Tuza, Z. (1994) Inequalities for minimal covering sets in set systems of given rank. Discrete Appl. Math. 51(1-2) 187–195.Google Scholar