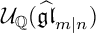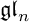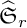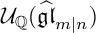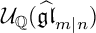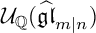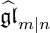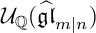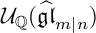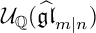43 results
The expansion and remaining suitable areas of global oil palm plantations
-
- Journal:
- Global Sustainability / Volume 7 / 2024
- Published online by Cambridge University Press:
- 19 February 2024, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fine mapping and discovery of candidate genes for rind trait in watermelon
-
- Journal:
- Plant Genetic Resources / Volume 21 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 01 December 2023, pp. 463-470
-
- Article
- Export citation
Protective factors for children with autism spectrum disorder during COVID-19-related strict lockdowns: a Shanghai autism early developmental cohort study
-
- Journal:
- Psychological Medicine / Volume 54 / Issue 6 / April 2024
- Published online by Cambridge University Press:
- 24 November 2023, pp. 1102-1112
-
- Article
- Export citation
Brain transcriptome-wide association study implicates novel risk genes underlying schizophrenia risk
-
- Journal:
- Psychological Medicine / Volume 53 / Issue 14 / October 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 6867-6877
-
- Article
- Export citation
Association of the plasma complement system with brain volume deficits in bipolar and major depressive disorders
-
- Journal:
- Psychological Medicine / Volume 53 / Issue 13 / October 2023
- Published online by Cambridge University Press:
- 26 October 2022, pp. 6102-6112
-
- Article
- Export citation
Dose–response relationship between dietary inflammatory index and diabetic kidney disease in US adults
-
- Journal:
- Public Health Nutrition / Volume 26 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 09 August 2022, pp. 611-619
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ameliorative patterns of grey matter in patients with first-episode and treatment-naïve schizophrenia
-
- Journal:
- Psychological Medicine / Volume 53 / Issue 8 / June 2023
- Published online by Cambridge University Press:
- 15 February 2022, pp. 3500-3510
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A REALIZATION OF THE ENVELOPING SUPERALGEBRA
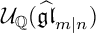 $ {\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})$
$ {\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 247 / September 2022
- Published online by Cambridge University Press:
- 09 September 2021, pp. 516-551
- Print publication:
- September 2022
-
- Article
- Export citation
Auditory event-related potentials, neurocognition, and global functioning in drug naïve first-episode schizophrenia and bipolar disorder
-
- Journal:
- Psychological Medicine / Volume 53 / Issue 3 / February 2023
- Published online by Cambridge University Press:
- 03 September 2021, pp. 785-794
-
- Article
- Export citation
Longitudinal trajectory analysis of antipsychotic response in patients with schizophrenia: 6-week, randomised, open-label, multicentre clinical trial – CORRIGENDUM
-
- Journal:
- BJPsych Open / Volume 7 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 20 August 2021, e153
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Protocol for a pharmacogenomic study on individualised antipsychotic drug treatment for patients with schizophrenia
-
- Journal:
- BJPsych Open / Volume 7 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 29 June 2021, e121
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relationship between changes in the course of COVID-19 and ratio of neutrophils-to-lymphocytes and related parameters in patients with severe vs. common disease
-
- Journal:
- Epidemiology & Infection / Volume 149 / 2021
- Published online by Cambridge University Press:
- 29 March 2021, e81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Longitudinal trajectory analysis of antipsychotic response in patients with schizophrenia: 6-week, randomised, open-label, multicentre clinical trial
-
- Journal:
- BJPsych Open / Volume 6 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 22 October 2020, e126
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Numerical methods for nonlocal and fractional models
-
- Journal:
- Acta Numerica / Volume 29 / May 2020
- Published online by Cambridge University Press:
- 30 November 2020, pp. 1-124
- Print publication:
- May 2020
-
- Article
- Export citation
Atomic-Scale Study of Intrinsic Defects Suppressing the Thermal Conductivity of Boron Arsenide
-
- Journal:
- Microscopy and Microanalysis / Volume 25 / Issue S2 / August 2019
- Published online by Cambridge University Press:
- 05 August 2019, pp. 942-943
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
A targeted drug delivery system based on carbon nanotubes loaded with lobaplatin toward liver cancer cells
-
- Journal:
- Journal of Materials Research / Volume 33 / Issue 17 / 14 September 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 2565-2575
- Print publication:
- 14 September 2018
-
- Article
- Export citation
Artificial Boundary Conditions for Nonlocal Heat Equations on Unbounded Domain
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 05 December 2016, pp. 16-39
- Print publication:
- January 2017
-
- Article
- Export citation
Dietary choline and betaine intake, choline-metabolising genetic polymorphisms and breast cancer risk: a case–control study in China
-
- Journal:
- British Journal of Nutrition / Volume 116 / Issue 6 / 28 September 2016
- Published online by Cambridge University Press:
- 04 August 2016, pp. 961-968
- Print publication:
- 28 September 2016
-
- Article
-
- You have access
- HTML
- Export citation
Calcium intake and breast cancer risk: meta-analysis of prospective cohort studies
-
- Journal:
- British Journal of Nutrition / Volume 116 / Issue 1 / 14 July 2016
- Published online by Cambridge University Press:
- 12 May 2016, pp. 158-166
- Print publication:
- 14 July 2016
-
- Article
-
- You have access
- HTML
- Export citation
Congenital Cholesteatoma Associated With Congenital Ossicular Anomalies: Presenting Author: Qiang Du
-
- Journal:
- The Journal of Laryngology & Otology / Volume 130 / Issue S3 / May 2016
- Published online by Cambridge University Press:
- 03 June 2016, p. S163
- Print publication:
- May 2016
-
- Article
-
- You have access
- HTML
- Export citation