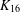 $K_{16}$
$K_{16}$
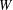 $W$-OPERATOR AND NONCROSSING PARTITIONS
$W$-OPERATOR AND NONCROSSING PARTITIONS
 $U$-NUMBERS IN FIELDS OF FORMAL POWER SERIES OVER FINITE FIELDS
$U$-NUMBERS IN FIELDS OF FORMAL POWER SERIES OVER FINITE FIELDS
 $p$-GROUPS ALL OF WHOSE NONNORMAL SUBGROUPS HAVE BOUNDED NORMAL CORES
$p$-GROUPS ALL OF WHOSE NONNORMAL SUBGROUPS HAVE BOUNDED NORMAL CORES
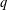 $q$-ANALOGUE OF A HYPERGEOMETRIC CONGRUENCE
$q$-ANALOGUE OF A HYPERGEOMETRIC CONGRUENCE