Research Article
Derivation of boundary conditions for the artificial boundaries associated with the solution of certain time dependent problems by Lax–Wendroff type difference schemes
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 1-18
-
- Article
-
- You have access
- Export citation
On cyclic subgroups of finite groups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 19-20
-
- Article
-
- You have access
- Export citation
Semisimple classes of alternative rings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 21-26
-
- Article
-
- You have access
- Export citation
A theorem on compatible N-groups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 27-30
-
- Article
-
- You have access
- Export citation
A remark on the nilpotency index of the radical of a group algebra of a p-solvable group
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 31-34
-
- Article
-
- You have access
- Export citation
Discontinuous homomorphisms and the separating space
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 35-39
-
- Article
-
- You have access
- Export citation
On positively complemented subspaces of c0
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 41-47
-
- Article
-
- You have access
- Export citation
Automatic discontinuity of intertwining operators
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 49-54
-
- Article
-
- You have access
- Export citation
Zero sets—consequences for primitive near-rings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 55-63
-
- Article
-
- You have access
- Export citation
Generators for the sporadic group Co3 as a (2, 3, 7) group
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 65-68
-
- Article
-
- You have access
- Export citation
A remark on the radical of a group algebra
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 69-71
-
- Article
-
- You have access
- Export citation
Embedding near-rings into polynomial near-rings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 73-79
-
- Article
-
- You have access
- Export citation
The subnormal subgroup structure of the infinite general linear group
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 81-86
-
- Article
-
- You have access
- Export citation
The weak-star closure of the unit ball in a subspace
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 87-95
-
- Article
-
- You have access
- Export citation
Rigid Artinian rings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 97-99
-
- Article
-
- You have access
- Export citation
The number of Cayley integers of given norm
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 101-103
-
- Article
-
- You have access
- Export citation
Book Reviews
A. W. Chatters and C. R. Hajarnavis, Rings with chain conditions (Pitman, 1980), £8·00.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 105
-
- Article
-
- You have access
- Export citation
Karl R. Stromberg, An Introduction to Classical Real Analysis (Wadsworth International Group, 1981), 576 pp., cloth, U.S. $29.95.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 105-106
-
- Article
-
- You have access
- Export citation
M. F. Atiyah , Representation Theory of Lie Groups (L.M.S. Lecture Note Series No. 34, C.U.P., 1980). £10.95.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 106
-
- Article
-
- You have access
- Export citation
R. L. E. Schwarzenberger N-dimensional crystallography (Pitman, Research Notes in Mathematics No. 41, 1980), £6.50.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 106-107
-
- Article
-
- You have access
- Export citation



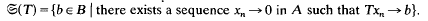
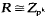 ,
,