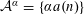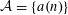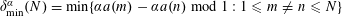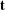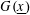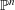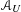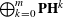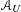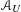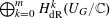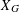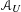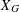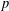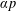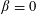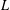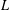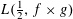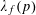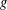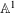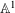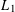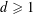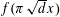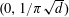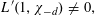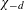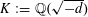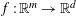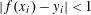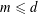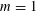Research Article
A UNIFIED APPROACH TO CONTINUOUS, MEASURABLE SELECTIONS, AND SELECTIONS FOR HYPERSPACES
- Part of:
-
- Published online by Cambridge University Press:
- 21 May 2018, pp. 607-627
-
- Article
- Export citation
A METRIC THEORY OF MINIMAL GAPS
- Part of:
-
- Published online by Cambridge University Press:
- 21 May 2018, pp. 628-636
-
- Article
- Export citation
DIFFERENTIAL GERSTENHABER–BATALIN–VILKOVISKY ALGEBRAS FOR CALABI–YAU HYPERSURFACE COMPLEMENTS
- Part of:
-
- Published online by Cambridge University Press:
- 07 June 2018, pp. 637-651
-
- Article
- Export citation
INTEGRAL MONODROMY GROUPS OF KLOOSTERMAN SHEAVES
- Part of:
-
- Published online by Cambridge University Press:
- 08 June 2018, pp. 652-678
-
- Article
- Export citation
ADDITIVE ENERGY AND THE METRIC POISSONIAN PROPERTY
- Part of:
-
- Published online by Cambridge University Press:
- 19 June 2018, pp. 679-700
-
- Article
- Export citation
TERNARY DIVISOR FUNCTIONS IN ARITHMETIC PROGRESSIONS TO SMOOTH MODULI
- Part of:
-
- Published online by Cambridge University Press:
- 19 June 2018, pp. 701-729
-
- Article
- Export citation
LIPSCHITZ EQUIVALENCE OF CANTOR SETS AND IRREDUCIBILITY OF POLYNOMIALS
- Part of:
-
- Published online by Cambridge University Press:
- 26 June 2018, pp. 730-741
-
- Article
- Export citation
FRACTIONAL PARTS OF POLYNOMIALS OVER THE PRIMES. II
- Part of:
-
- Published online by Cambridge University Press:
- 26 June 2018, pp. 742-769
-
- Article
- Export citation
LEVEL RECIPROCITY IN THE TWISTED SECOND MOMENT OF RANKIN–SELBERG
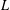 $L$-FUNCTIONS
$L$-FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 26 June 2018, pp. 770-784
-
- Article
- Export citation
RIGID LOCAL SYSTEMS ON
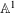 $\mathbb{A}^{1}$ WITH FINITE MONODROMY
$\mathbb{A}^{1}$ WITH FINITE MONODROMY
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2018, pp. 785-846
-
- Article
- Export citation
A CODING OF BUNDLE GRAPHS AND THEIR EMBEDDINGS INTO BANACH SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 06 August 2018, pp. 847-874
-
- Article
- Export citation
TRANSCENDENTAL SUMS RELATED TO THE ZEROS OF ZETA FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2018, pp. 875-897
-
- Article
- Export citation
CONTROLLING LIPSCHITZ FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 02 August 2018, pp. 898-910
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
MTK volume 64 Issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 01 October 2018, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
MTK volume 64 Issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 01 October 2018, pp. b1-b2
-
- Article
-
- You have access
- Export citation