Article contents
TERNARY DIVISOR FUNCTIONS IN ARITHMETIC PROGRESSIONS TO SMOOTH MODULI
Published online by Cambridge University Press: 19 June 2018
Abstract
We prove that the exponent of distribution of 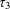 $\unicode[STIX]{x1D70F}_{3}$ in arithmetic progressions can be as large as
$\unicode[STIX]{x1D70F}_{3}$ in arithmetic progressions can be as large as 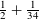 $\frac{1}{2}+\frac{1}{34}$, provided that the moduli is squarefree and has only sufficiently small prime factors. The tools involve arithmetic exponent pairs for algebraic trace functions, as well as a double
$\frac{1}{2}+\frac{1}{34}$, provided that the moduli is squarefree and has only sufficiently small prime factors. The tools involve arithmetic exponent pairs for algebraic trace functions, as well as a double 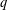 $q$-analogue of the van der Corput method for smooth bilinear forms.
$q$-analogue of the van der Corput method for smooth bilinear forms.
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2018
References
- 4
- Cited by




