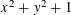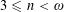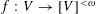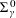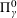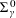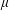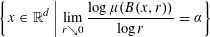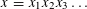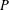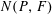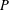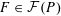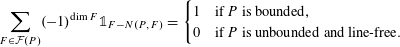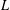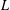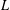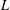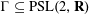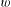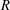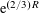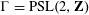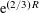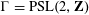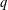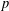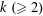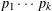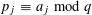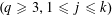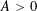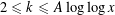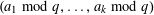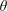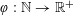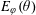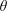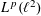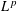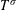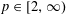Research Article
A LOCAL UNIQUENESS THEOREM FOR MINIMIZERS OF PETTY’S CONJECTURED PROJECTION INEQUALITY
- Part of:
-
- Published online by Cambridge University Press:
- 24 January 2018, pp. 1-19
-
- Article
- Export citation
THE GOLDBACH PROBLEM FOR PRIMES THAT ARE SUMS OF TWO SQUARES PLUS ONE
- Part of:
-
- Published online by Cambridge University Press:
- 25 January 2018, pp. 20-70
-
- Article
- Export citation
SET MAPPINGS WITH FREE SETS WHICH ARE ARITHMETIC PROGRESSIONS
- Part of:
-
- Published online by Cambridge University Press:
- 06 February 2018, pp. 71-76
-
- Article
- Export citation
ON THE
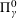 $\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FE}}^{0}$-COMPLETENESS AND
$\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FE}}^{0}$-COMPLETENESS AND 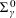 $\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FE}}^{0}$-COMPLETENESS OF MULTIFRACTAL DECOMPOSITION SETS
$\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FE}}^{0}$-COMPLETENESS OF MULTIFRACTAL DECOMPOSITION SETS
- Part of:
-
- Published online by Cambridge University Press:
- 06 February 2018, pp. 77-114
-
- Article
- Export citation
MONOCHROMATIC FACTORIZATIONS OF WORDS AND PERIODICITY
- Part of:
-
- Published online by Cambridge University Press:
- 06 February 2018, pp. 115-123
-
- Article
- Export citation
AN INCLUSION–EXCLUSION IDENTITY FOR NORMAL CONES OF POLYHEDRAL SETS
- Part of:
-
- Published online by Cambridge University Press:
- 05 February 2018, pp. 124-136
-
- Article
- Export citation
TRUNCATED PRODUCT REPRESENTATIONS FOR
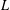 $L$-FUNCTIONS IN THE HYPERELLIPTIC ENSEMBLE
$L$-FUNCTIONS IN THE HYPERELLIPTIC ENSEMBLE
- Part of:
-
- Published online by Cambridge University Press:
- 06 February 2018, pp. 137-158
-
- Article
- Export citation
LOCAL AVERAGE OF THE HYPERBOLIC CIRCLE PROBLEM FOR FUCHSIAN GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 06 February 2018, pp. 159-183
-
- Article
- Export citation
KERNEL FUNCTIONS OF THE TWISTED SYMMETRIC SQUARE OF ELLIPTIC MODULAR FORMS
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2018, pp. 184-210
-
- Article
- Export citation
COMPARISON OF WEAK AND STRONG MOMENTS FOR VECTORS WITH INDEPENDENT COORDINATES
- Part of:
-
- Published online by Cambridge University Press:
- 14 February 2018, pp. 211-229
-
- Article
- Export citation
THE PRIMES ARE NOT METRIC POISSONIAN
- Part of:
-
- Published online by Cambridge University Press:
- 14 February 2018, pp. 230-236
-
- Article
- Export citation
LARGE BIAS FOR INTEGERS WITH PRIME FACTORS IN ARITHMETIC PROGRESSIONS
- Part of:
-
- Published online by Cambridge University Press:
- 15 February 2018, pp. 237-252
-
- Article
- Export citation
CLASSIFICATION OF SPIN STRUCTURES ON FOUR-DIMENSIONAL ALMOST-FLAT MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 14 February 2018, pp. 253-266
-
- Article
- Export citation
HAUSDORFF DIMENSION OF THE SET APPROXIMATED BY IRRATIONAL ROTATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 14 February 2018, pp. 267-283
-
- Article
- Export citation
A TWO-WEIGHT INEQUALITY BETWEEN
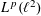 $L^{p}(\ell ^{2})$ AND
$L^{p}(\ell ^{2})$ AND 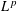 $L^{p}$
$L^{p}$
- Part of:
-
- Published online by Cambridge University Press:
- 14 February 2018, pp. 284-302
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
MTK volume 64 Issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 05 March 2018, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
MTK volume 64 Issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 05 March 2018, pp. b1-b2
-
- Article
-
- You have access
- Export citation