No CrossRef data available.
Article contents
SET MAPPINGS WITH FREE SETS WHICH ARE ARITHMETIC PROGRESSIONS
Published online by Cambridge University Press: 06 February 2018
Abstract
If 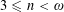 $3\leqslant n<\unicode[STIX]{x1D714}$ and
$3\leqslant n<\unicode[STIX]{x1D714}$ and 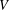 $V$ is a vector space over
$V$ is a vector space over 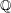 $\mathbb{Q}$ with
$\mathbb{Q}$ with 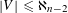 $|V|\leqslant \aleph _{n-2}$, then there is a well ordering of
$|V|\leqslant \aleph _{n-2}$, then there is a well ordering of 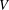 $V$ such that every vector is the last element of only finitely many length-
$V$ such that every vector is the last element of only finitely many length- $n$ arithmetic progressions (
$n$ arithmetic progressions ( $n$-APs). This implies that there is a set mapping
$n$-APs). This implies that there is a set mapping 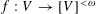 $f:V\rightarrow [V]^{{<}\unicode[STIX]{x1D714}}$ with no free set which is an
$f:V\rightarrow [V]^{{<}\unicode[STIX]{x1D714}}$ with no free set which is an  $n$-AP. If, however,
$n$-AP. If, however, 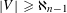 $|V|\geqslant \aleph _{n-1}$, then for every set mapping
$|V|\geqslant \aleph _{n-1}$, then for every set mapping 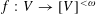 $f:V\rightarrow [V]^{{<}\unicode[STIX]{x1D714}}$ there is a free set which is an
$f:V\rightarrow [V]^{{<}\unicode[STIX]{x1D714}}$ there is a free set which is an  $n$-AP.
$n$-AP.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2018




