Research Article
Angle-sum relations for polyhedral sets
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 173-188
-
- Article
- Export citation
Correction
Isoperimetric problems for tilings, corrigendum
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 189-191
-
- Article
- Export citation
Research Article
An indecomposable polytope all of whose facets are decomposable
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 192-196
-
- Article
- Export citation
An upper estimate for the lattice point enumerator
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 197-203
-
- Article
- Export citation
Norm form equations IV: Rational functions
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 204-211
-
- Article
- Export citation
Large gaps between zeros of the zeta-function
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 212-238
-
- Article
- Export citation
A note on the Kronecker limit formula for real quadratic fields
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 239-243
-
- Article
- Export citation
Least primitive roots modulo the square of a prime ideal
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 244-251
-
- Article
- Export citation
Ranks of differentiable functions
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 252-278
-
- Article
- Export citation
d-sequences, local cohomology modules and generalized analytic independence
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 279-284
-
- Article
- Export citation
On generalized Dedekind domains
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 285-295
-
- Article
- Export citation
Book Reviews
Book Reviews - H. Abelson and A. diSessa. Turtle Geometry. MIT Press. 1986, 477 pp., £10·95. - M. Altman. A Unified Theory of Nonlinear Operator and Evolution Equations with Applications. Marcel Dekker. 1986, 292 pp., $83.50. - R. C. Baker. Diophantine Inequalities. London Math. Soc. Monographs, New Series, No. 1. Oxford University Press. 1986, 275 pp., £32. - T. S. Blyth and E. F. Robertson. Essential Student Algebra. 1 Sets and Mappings, 2 Matrices and Vector Spaces, 3 Abstract Algebra, 4 Linear Algebra, 5 Groups. Chapman and Hall. 1986, 120 pp each, £3·95 each. - J. H. Carruth, J. A. Hildebrant and R. J. Koch. The Theory of Topological Semigroups, Vol. 2. Marcel Dekker. 1986, 195pp., $59·29. - D. Eisenbud and W. Neumann. Three Dimensional Link Theory and Invariants of Plane Curve Singularities. Annals of Math. Studies no. 110. Princeton University Press. 1985, 172pp., £28·30, paperback £10·30. - C. F. Gardiner. Algebraic Structures. Ellis Horwood. 1986, 280pp., paperback £14·50. - P. R. Halmos. I Want to be a Mathematician. Springer. 1985, 421pp., DM 134. - R. Hill. A First Course in Coding Theory. Oxford University Press. 1986, 251pp, £25, paperback £12·50. - R. Maude. Mathematical Analysis. Edward Arnold. 1986, 224pp., £11·75. - S. G. Mikhlin. Constants in Some Inequalities of Analysis. J. Wiley & Sons.1986, 108pp., £13·75. - K. W. Morton and M. J. Baines, Editors. Numerical Methods for Fluid Dynamics II. Oxford University Press. 1986, 679pp., £60. - G. Saccheri. Euclides Vindicatus, 2nd English Edition. Chelsea. 1986, 255pp., $16·95. - V. M. Tikhomirov. Fundamental Principles of the Theory of Extremal Problems. J. Wiley & Sons.1986, 136pp., £13.95. - B. L. van der Waerden. A History of Algebra. Springer. 1985, 271pp., DM98. - P. L. Walker. The Theory of Fourier Series and Integrals. Wiley-Interscience. 1986, 192pp., £14·95.
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 296-298
-
- Article
- Export citation
Index
Index to volume 33
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 299
-
- Article
- Export citation
Front matter
MTK volume 33 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f3
-
- Article
-
- You have access
- Export citation

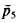 and
and 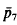 , and ā
, and ā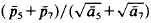 was equal to 3.7263… This being greater than √8√3 = 3–7224… the tiling given in [1] does not yield the desired counter-example. In what follows we shall construct a tiling for which the respective quotient will turn out to be less than √8√3.
was equal to 3.7263… This being greater than √8√3 = 3–7224… the tiling given in [1] does not yield the desired counter-example. In what follows we shall construct a tiling for which the respective quotient will turn out to be less than √8√3.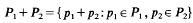
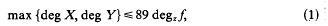
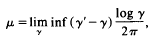
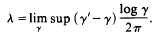
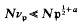
 to denote, for
to denote, for