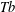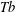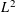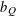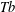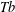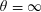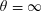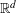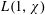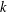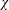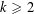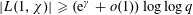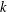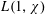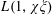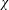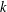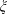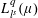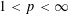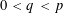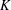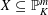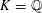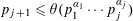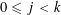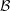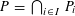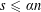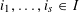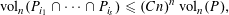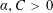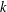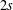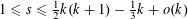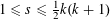Research Article
GENERALIZED LOCAL
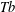 $\mathit{Tb}$ THEOREMS FOR SQUARE FUNCTIONS
$\mathit{Tb}$ THEOREMS FOR SQUARE FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 25 July 2016, pp. 1-28
-
- Article
- Export citation
THE
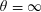 $\unicode[STIX]{x1D703}=\infty$ CONJECTURE IMPLIES THE RIEMANN HYPOTHESIS
$\unicode[STIX]{x1D703}=\infty$ CONJECTURE IMPLIES THE RIEMANN HYPOTHESIS
- Part of:
-
- Published online by Cambridge University Press:
- 26 July 2016, pp. 29-33
-
- Article
- Export citation
RESTRICTED SIMULTANEOUS DIOPHANTINE APPROXIMATION
- Part of:
-
- Published online by Cambridge University Press:
- 26 July 2016, pp. 34-52
-
- Article
- Export citation
LARGE VALUES OF
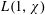 $L(1,\unicode[STIX]{x1D712})$ FOR
$L(1,\unicode[STIX]{x1D712})$ FOR 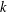 $k$TH ORDER CHARACTERS
$k$TH ORDER CHARACTERS 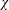 $\unicode[STIX]{x1D712}$ AND APPLICATIONS TO CHARACTER SUMS
$\unicode[STIX]{x1D712}$ AND APPLICATIONS TO CHARACTER SUMS
- Part of:
-
- Published online by Cambridge University Press:
- 26 July 2016, pp. 53-71
-
- Article
- Export citation
TWO-WEIGHT NORM INEQUALITIES FOR VECTOR-VALUED OPERATORS
- Part of:
-
- Published online by Cambridge University Press:
- 26 July 2016, pp. 72-91
-
- Article
- Export citation
FORMS OF DIFFERING DEGREES OVER NUMBER FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 26 September 2016, pp. 92-123
-
- Article
- Export citation
SHAPES OF POLYHEDRA, MIXED VOLUMES AND HYPERBOLIC GEOMETRY
- Part of:
-
- Published online by Cambridge University Press:
- 23 September 2016, pp. 124-183
-
- Article
- Export citation
CLOSED SETS WITH THE KAKEYA PROPERTY
- Part of:
-
- Published online by Cambridge University Press:
- 23 September 2016, pp. 184-195
-
- Article
- Export citation
SHIFTED MOMENTS OF
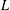 $L$-FUNCTIONS AND MOMENTS OF THETA FUNCTIONS
$L$-FUNCTIONS AND MOMENTS OF THETA FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 27 September 2016, pp. 196-212
-
- Article
- Export citation
A SIEVE PROBLEM AND ITS APPLICATION
- Part of:
-
- Published online by Cambridge University Press:
- 27 September 2016, pp. 213-229
-
- Article
- Export citation
PERFECT POWERS THAT ARE SUMS OF CONSECUTIVE CUBES
- Part of:
-
- Published online by Cambridge University Press:
- 05 October 2016, pp. 230-249
-
- Article
- Export citation
INTRINSIC DIOPHANTINE APPROXIMATION ON GENERAL POLYNOMIAL SURFACES
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 250-259
-
- Article
- Export citation
A FLAG VECTOR OF A 3-SPHERE THAT IS NOT THE FLAG VECTOR OF A 4-POLYTOPE
- Part of:
-
- Published online by Cambridge University Press:
- 08 December 2016, pp. 260-271
-
- Article
- Export citation
BRASCAMP–LIEB INEQUALITY AND QUANTITATIVE VERSIONS OF HELLY’S THEOREM
- Part of:
-
- Published online by Cambridge University Press:
- 07 December 2016, pp. 272-291
-
- Article
- Export citation
APPROXIMATING THE MAIN CONJECTURE IN VINOGRADOV’S MEAN VALUE THEOREM
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2016, pp. 292-350
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
MTK volume 63 Issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 01 February 2017, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
MTK volume 63 Issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 01 February 2017, pp. b1-b4
-
- Article
-
- You have access
- Export citation