Article contents
THE 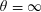 $\unicode[STIX]{x1D703}=\infty$ CONJECTURE IMPLIES THE RIEMANN HYPOTHESIS
$\unicode[STIX]{x1D703}=\infty$ CONJECTURE IMPLIES THE RIEMANN HYPOTHESIS
Published online by Cambridge University Press: 26 July 2016
Abstract
We show that the 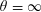 $\unicode[STIX]{x1D703}=\infty$ conjecture implies the Riemann hypothesis.
$\unicode[STIX]{x1D703}=\infty$ conjecture implies the Riemann hypothesis.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2016
References
- 5
- Cited by




