Research Article
Thin equivalence relations and effective decompositions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1153-1164
-
- Article
- Export citation
A remark on locally pure measures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1165-1170
-
- Article
- Export citation
On closed P-sets with ccc in the space ω*
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1171-1176
-
- Article
- Export citation
Nonisomorphism of lattices of recursively enumerable sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1177-1188
-
- Article
- Export citation
On the existence of atomic models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1189-1194
-
- Article
- Export citation
A note on Mathematics of infinity
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1195-1200
-
- Article
- Export citation
Stationary subsets of [ℵω]<ωn
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1201-1218
-
- Article
- Export citation
Boolean universes above Boolean models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1219-1250
-
- Article
- Export citation
A relativization mechanism in recursion categories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1251-1267
-
- Article
- Export citation
A very discontinuous Borel function
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1268-1283
-
- Article
- Export citation
Amoeba-absoluteness and projective measurability
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1284-1290
-
- Article
- Export citation
Forcing isomorphism
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1291-1301
-
- Article
- Export citation
S-homogeneity and automorphism groups
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1302-1322
-
- Article
- Export citation
Strong measure zero sets without Cohen reals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1323-1341
-
- Article
- Export citation
Hyper-regular lattice-ordered groups
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1342-1358
-
- Article
- Export citation
An existence theorem for a special ultrafilter when 𝔡 = 𝔠
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1359-1364
-
- Article
- Export citation
Counting the maximal intermediate constructive logics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1365-1401
-
- Article
- Export citation
On the number of automorphisms of uncountable models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1402-1418
-
- Article
- Export citation
Addendum to “A structure theorem for strongly abelian varieties”
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1419-1425
-
- Article
- Export citation
Belief contraction in the context of the general theory of rational choice
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1426-1450
-
- Article
- Export citation



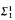 equivalence relation for which there does not exist a perfect set of inequivalent reals. If 0* exists or if
equivalence relation for which there does not exist a perfect set of inequivalent reals. If 0* exists or if 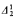 well-ordering of the equivalence classes.
well-ordering of the equivalence classes.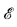 be the lattice of recursively enumerable subsets of
be the lattice of recursively enumerable subsets of 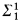 (see, for example, Shoenfield [11] for a definition of what it means for a set
(see, for example, Shoenfield [11] for a definition of what it means for a set 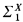 but not
but not 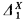 and then applied a theorem of Lachlan [6] (definitions of
and then applied a theorem of Lachlan [6] (definitions of 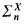 and
and 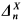 Boolean algebras will be given in §2). Feiner's result is of particular interest for the case
Boolean algebras will be given in §2). Feiner's result is of particular interest for the case 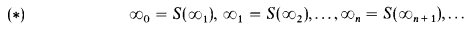
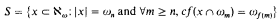
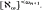
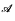 on ℵ
on ℵ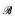 ≺
≺ 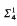 -Amoeba-absoluteness implies that
-Amoeba-absoluteness implies that 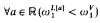 and, hence,
and, hence, 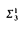 measurability. This answers a question of Haim Judah (private communication).
measurability. This answers a question of Haim Judah (private communication).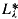 . (
. (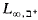 by adding for each μ < λ a quantifier saying the dimension of a dependence structure is greater than μ) Further work ([3], [2]) shows that ⊐
by adding for each μ < λ a quantifier saying the dimension of a dependence structure is greater than μ) Further work ([3], [2]) shows that ⊐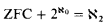 :
: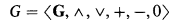
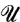 , consider the ultrapower
, consider the ultrapower 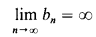
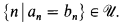
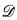 is a subset of
is a subset of 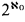 .
.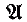 ) denote the number of automorphisms of a model
) denote the number of automorphisms of a model 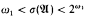 . We study the sufficiency of some conditions for
. We study the sufficiency of some conditions for 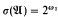 . These conditions are analogous to conditions studied by D. Kueker in connection with countable models.
. These conditions are analogous to conditions studied by D. Kueker in connection with countable models.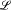 , containing only function symbols, which is closed under homomorphisms, submodels, and products. A variety
, containing only function symbols, which is closed under homomorphisms, submodels, and products. A variety 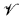 is said to be strongly abelian if for any term
is said to be strongly abelian if for any term 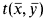 in
in