Research Article
ℵ0-categorical structures with arbitrarily fast growth of algebraic closure
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 897-909
-
- Article
- Export citation
Some results on permutation group isomorphism and categoricity
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 910-914
-
- Article
- Export citation
Blowing up the power set of the least measurable
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 915-923
-
- Article
- Export citation
0# and inner models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 924-932
-
- Article
- Export citation
PDL has interpolation
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 933-946
-
- Article
- Export citation
Defining transcendentals in function fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 947-956
-
- Article
- Export citation
Properties of forking in ω-free pseudo-algebraically closed fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 957-996
-
- Article
- Export citation
The theory of modules of separably closed fields 1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 997-1015
-
- Article
- Export citation
On the binding group in simple theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1016-1024
-
- Article
- Export citation
Generic variations of models of T
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1025-1038
-
- Article
- Export citation
Representability in second-order propositional poly-modal logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1039-1054
-
- Article
- Export citation
Isolation and lattice embeddings
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1055-1064
-
- Article
- Export citation
The lazy logic of partial terms
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1065-1077
-
- Article
- Export citation
Generalized r-cohesiveness and the arithmetical hierarchy: a correction to “Generalized cohesiveness”
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1078-1082
-
- Article
- Export citation
Strong convergence in finite model theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1083-1092
-
- Article
- Export citation
On polynomial time computation over unordered structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1093-1125
-
- Article
- Export citation
The torsionfree part of the Ziegler spectrum of RG when R is a Dedekind domain and G is a finite group
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1126-1140
-
- Article
- Export citation
Bounded Martin's Maximum, weak Erdӧs cardinals, and ψAc
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1141-1152
-
- Article
- Export citation
Transfinite dependent choice and ω-model reflection
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1153-1168
-
- Article
- Export citation
On regular reduced products*
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1169-1177
-
- Article
- Export citation



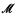 on the set of unordered
on the set of unordered 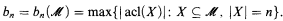
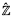 , and gave elementary invariants for their first order theory, thereby proving the decidability of the theory of finite fields. Ax's results were then extended to a larger class of PAC fields by M. Jarden and U. Kiehne [21], and Jarden [19]. The final word on theories of PAC fields was given by G. Cherlin, L. van den Dries and A. Macintyre [10], see also results by Ju. Ershov [13], [14]. Let
, and gave elementary invariants for their first order theory, thereby proving the decidability of the theory of finite fields. Ax's results were then extended to a larger class of PAC fields by M. Jarden and U. Kiehne [21], and Jarden [19]. The final word on theories of PAC fields was given by G. Cherlin, L. van den Dries and A. Macintyre [10], see also results by Ju. Ershov [13], [14]. Let 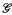
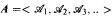 of finite models, where the universe of
of finite models, where the universe of 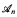 , is {1,2,…,
, is {1,2,…,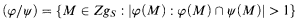
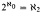 . We also prove that
. We also prove that  of cardinality ≤
of cardinality ≤