Article contents
Bounded Martin's Maximum, weak Erdӧs cardinals, and ψAc
Published online by Cambridge University Press: 12 March 2014
Abstract
We prove that a form of the Erdӧs property (consistent with V = L[Hω2] and strictly weaker than the Weak Chang's Conjecture at ω1), together with Bounded Martin's Maximum implies that Woodin's principle ψAC holds, and therefore 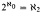 . We also prove that ψAC implies that every function f: ω1 → ω1 is bounded by some canonical function on a club and use this to produce a model of the Bounded Semiproper Forcing Axiom in which Bounded Martin's Maximum fails.
. We also prove that ψAC implies that every function f: ω1 → ω1 is bounded by some canonical function on a club and use this to produce a model of the Bounded Semiproper Forcing Axiom in which Bounded Martin's Maximum fails.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2002
References
REFERENCES
- 7
- Cited by


