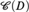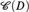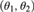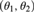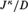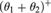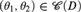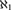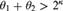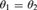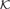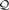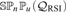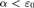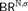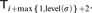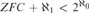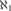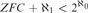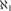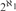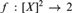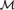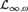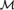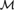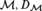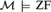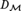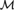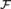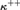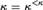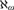Articles
WEAK SQUARES AND VERY GOOD SCALES
-
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1-12
-
- Article
- Export citation
JUMP OPERATIONS FOR BOREL GRAPHS
-
- Published online by Cambridge University Press:
- 01 May 2018, pp. 13-28
-
- Article
- Export citation
ON CUTS IN ULTRAPRODUCTS OF LINEAR ORDERS II
-
- Published online by Cambridge University Press:
- 01 May 2018, pp. 29-39
-
- Article
- Export citation
DOMINIONS AND PRIMITIVE POSITIVE FUNCTIONS
-
- Published online by Cambridge University Press:
- 05 February 2018, pp. 40-54
-
- Article
- Export citation
STRICT COHERENCE ON MANY-VALUED EVENTS
-
- Published online by Cambridge University Press:
- 12 February 2018, pp. 55-69
-
- Article
-
- You have access
- Export citation
A DIRECT PROOF OF SCHWICHTENBERG’S BAR RECURSION CLOSURE THEOREM
-
- Published online by Cambridge University Press:
- 12 February 2018, pp. 70-83
-
- Article
- Export citation
THE NUMBER OF ATOMIC MODELS OF UNCOUNTABLE THEORIES
-
- Published online by Cambridge University Press:
- 08 February 2018, pp. 84-102
-
- Article
- Export citation
DEGREES OF CATEGORICITY AND SPECTRAL DIMENSION
-
- Published online by Cambridge University Press:
- 01 May 2018, pp. 103-116
-
- Article
- Export citation
ON MAXIMAL STABLE QUOTIENTS OF DEFINABLE GROUPS IN NIP THEORIES
-
- Published online by Cambridge University Press:
- 08 February 2018, pp. 117-122
-
- Article
- Export citation
THE DEFINABLE (P, Q)-THEOREM FOR DISTAL THEORIES
-
- Published online by Cambridge University Press:
- 09 November 2017, pp. 123-127
-
- Article
- Export citation
DECIDING THE CHROMATIC NUMBERS OF ALGEBRAIC HYPERGRAPHS
-
- Published online by Cambridge University Press:
- 01 May 2018, pp. 128-145
-
- Article
- Export citation
ZFC PROVES THAT THE CLASS OF ORDINALS IS NOT WEAKLY COMPACT FOR DEFINABLE CLASSES
-
- Published online by Cambridge University Press:
- 01 May 2018, pp. 146-164
-
- Article
- Export citation
COMPACT METRIZABLE STRUCTURES AND CLASSIFICATION PROBLEMS
-
- Published online by Cambridge University Press:
- 01 May 2018, pp. 165-186
-
- Article
- Export citation
THERE ARE NO INTERMEDIATE STRUCTURES BETWEEN THE GROUP OF INTEGERS AND PRESBURGER ARITHMETIC
-
- Published online by Cambridge University Press:
- 01 May 2018, pp. 187-207
-
- Article
- Export citation
COHERENT SYSTEMS OF FINITE SUPPORT ITERATIONS
-
- Published online by Cambridge University Press:
- 05 February 2018, pp. 208-236
-
- Article
- Export citation
LEFT-ORDERABLE COMPUTABLE GROUPS
-
- Published online by Cambridge University Press:
- 05 February 2018, pp. 237-255
-
- Article
- Export citation
HIERARCHIES OF FORCING AXIOMS, THE CONTINUUM HYPOTHESIS AND SQUARE PRINCIPLES
-
- Published online by Cambridge University Press:
- 01 May 2018, pp. 256-282
-
- Article
- Export citation
HIERARCHIES OF (VIRTUAL) RESURRECTION AXIOMS
-
- Published online by Cambridge University Press:
- 01 May 2018, pp. 283-325
-
- Article
- Export citation
A COMPUTABLE FUNCTOR FROM GRAPHS TO FIELDS
-
- Published online by Cambridge University Press:
- 01 May 2018, pp. 326-348
-
- Article
- Export citation
THE EIGHTFOLD WAY
-
- Published online by Cambridge University Press:
- 01 May 2018, pp. 349-371
-
- Article
- Export citation