Hostname: page-component-8448b6f56d-cfpbc Total loading time: 0 Render date: 2024-04-19T05:40:24.185Z Has data issue: false hasContentIssue false
  • English
  • Français

A COMPUTABLE FUNCTOR FROM GRAPHS TO FIELDS

Published online by Cambridge University Press:  01 May 2018

RUSSELL MILLER ,
BJORN POONEN ,
HANS SCHOUTENS  and
ALEXANDRA SHLAPENTOKH
RUSSELL MILLER
Affiliation:
DEPARTMENT OF MATHEMATICS QUEENS COLLEGE 65-30 KISSENA BLVD. QUEENS, NY 11367, USA and PH.D. PROGRAMS IN MATHEMATICS AND COMPUTER SCIENCE CUNY GRADUATE CENTER 365 FIFTH AVENUE NEW YORK, NY10016, USAE-mail:russell.Miller@qc.cuny.eduURL: http://qcpages.qc.cuny.edu/∼rmiller
BJORN POONEN
Affiliation:
DEPARTMENT OF MATHEMATICS MASSACHUSETTS INSTITUTE OF TECHNOLOGY CAMBRIDGE, MA02139-4307, USAE-mail:poonen@math.mit.eduURL: http://math.mit.edu/∼poonen
HANS SCHOUTENS
Affiliation:
DEPARTMENT OF MATHEMATICS NEW YORK CITY COLLEGE OF TECHNOLOGY 300 JAY STREET BROOKLYN, NY 11201, USA and PH.D. PROGRAM IN MATHEMATICS CUNY GRADUATE CENTER 365 FIFTH AVENUE NEW YORK, NY10016, USAE-mail:hschoutens@citytech.cuny.edu
ALEXANDRA SHLAPENTOKH
Affiliation:
DEPARTMENT OF MATHEMATICS EAST CAROLINA UNIVERSITY GREENVILLE, NC27858, USAE-mail:shlapentokha@ecu.eduURL: http://myweb.ecu.edu/shlapentokha/
Get access Rights & Permissions [Opens in a new window]

Abstract

Fried and Kollár constructed a fully faithful functor from the category of graphs to the category of fields. We give a new construction of such a functor and use it to resolve a longstanding open problem in computable model theory, by showing that for every nontrivial countable structure ${\cal S}$, there exists a countable field 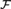${\cal F}$ of arbitrary characteristic with the same essential computable-model-theoretic properties as ${\cal S}$. Along the way, we develop a new “computable category theory”, and prove that our functor and its partially defined inverse (restricted to the categories of countable graphs and countable fields) are computable functors.

Keywords

Primary 03C57Secondary 03D4512L1218A1508A35completenesscomputabilitycomputable model theoryfieldsfunctorgraphs
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 1 , March 2018 , pp. 326 - 348
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ash, C. J. and Knight, J. F., Computable Structures and the Hyperarithmetical Hierarchy, Elsevier, Amsterdam, 2000.Google Scholar
Downey, R. G. and Jockusch, C. G. Jr., Every low Boolean algebra is isomorphic to a recursive one. Proceedings of the American Mathematical Society, vol. 122 (1994), pp. 871–880.CrossRefGoogle Scholar
Downey, R. G., Kach, A. M., Lempp, S., Lewis-Pye, A. E. M., Montalbán, A., and Turetsky, D. D., The complexity of computable categoricity. Advances in Mathematics, vol. 268 (2015), pp. 423–466.Google Scholar
Fokina, E., Kalimullin, I., and Miller, R., Degrees of categoricity of computable structures. Archive for Mathematical Logic, vol. 49 (2010), pp. 51–67.Google Scholar
Fried, E. and Kollár, J., Automorphism groups of fields, Universal Algebra (Esztergom, 1977), Colloquia Mathematica Societatis János Bolyai, vol. 29, North-Holland, Amsterdam-New York, 1982, pp. 293–303.Google Scholar
Goncharov, S. S., The quantity of nonautoequivalent constructivizations. Algebra and Logic, vol. 16 (1977), pp. 169–185.Google Scholar
Goncharov, S. S., The problem of the number of nonautoequivalent constructivizations. Algebra and Logic, vol. 19 (1980), pp. 401–414.Google Scholar
Goncharov, S. S., Groups with a finite number of constructivizations. Soviet Mathematics Doklady, vol. 23 (1981), pp. 58–61.Google Scholar
Goncharov, S. S. and Dzgoev, V. D., Autostability of models. Algebra and Logic, vol. 19 (1980), pp. 45–58 (Russian), 28–37 (English translation).Google Scholar
Green, B., Bounds on the number of automorphisms of curves over algebraically closed fields. Israel Journal of Mathematics, vol. 194 (2013), no. 1, pp. 69–76.Google Scholar
Harizanov, V. and Miller, R., Spectra of structures and relations, this Journal, vol. 72 (2007), pp. 324–348.Google Scholar
Harizanov, V., Miller, R., and Morozov, A., Simple structures with complex symmetry. Algebra and Logic, vol. 49 (2010), pp. 68–90.Google Scholar
Harrison-Trainor, M., Melnikov, A., Miller, R., and Montalbán, A., Computable functors and effective interpretability, this Journal, vol. 82 (2017), no. 1, pp. 77–97.Google Scholar
Hartshorne, R., Algebraic Geometry, Graduate Texts in Mathematics, vol. 52, Springer-Verlag, New York, 1977.Google Scholar
Hirschfeldt, D. R., Khoussainov, B., Shore, R. A., and Slinko, A. M., Degree spectra and computable dimensions in algebraic structures. Annals of Pure and Applied Logic, vol. 115 (2002), pp. 71–113.Google Scholar
Hirschfeldt, D. R., Kramer, K., Miller, R., and Shlapentokh, A., Categoricity properties for computable algebraic fields. Transactions of the American Mathematical Society, vol. 367 (2015), pp. 3955–3980.Google Scholar
Jockusch, C. G. and Soare, R., Degrees of orderings not isomorphic to recursive linear orderings. Annals of Pure and Applied Logic, vol. 52 (1991), pp. 39–64.Google Scholar
Knight, J. F., Degrees coded in jumps of orderings, this Journal, vol. 51 (1986), pp. 1034–1042.Google Scholar
Knight, J. F., Miller, S., and Vanden Boom, M., Turing computable embeddings, this Journal, 72 (2007), no. 3, pp. 901–918.Google Scholar
Lang, S., Integral points on curves. Publications Mathématiques de l’IHÉS, vol. 6 (1960), pp. 27–43.Google Scholar
Lempp, S., McCoy, C., Miller, R., and Solomon, R., Computable categoricity of trees of finite height, this Journal, vol. 70 (2005), pp. 151–215.Google Scholar
Levin, O., Computability theory, reverse mathematics and ordered fields, Ph.D. thesis, University of Connecticut, 2009.Google Scholar
Marker, D., Non-${{\rm{\Sigma }}_n}$-axiomatizable almost strongly minimal theories, this Journal, vol. 54 (1989), pp. 921–927.Google Scholar
Miller, R., d-Computable categoricity for algebraic fields, this Journal, vol. 74 (2009), pp. 1325–1351.Google Scholar
Miller, R. and Schoutens, H., Computably categorical fields via Fermat’s Last Theorem. Computability, vol. 2 (2013), pp. 51–65.Google Scholar
Montalbán, A., Computability theoretic classifications for classes of structures. Proceedings of the ICM 2014, vol. 2 (2014), pp. 79–101.Google Scholar
Poonen, B., Varieties without extra automorphisms. III. Hypersurfaces. Finite Fields and their Applications, vol. 11 (2005), no. 2, pp. 230–268.Google Scholar
Pour-El, M. B. and Ian Richards, J., Computability in Analysis and Physics, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1989.CrossRefGoogle Scholar
Pröhle, P., Does the Frobenius endomorphism always generate a direct summand in the endomorphism monoids of fields of prime characteristic? Bulletin of the Australian Mathematical Society, vol. 30 (1984), no. 3, pp. 335–356.Google Scholar
Remmel, J. B., Recursively categorical linear orderings. Proceedings of the American Mathematical Society, vol. 83 (1981), pp. 387–391.Google Scholar
Richter, L. J., Degrees of structures, this Journal, vol. 46 (1981), pp. 723–731.Google Scholar
Samuel, P., Compléments à un article de Hans Grauert sur la conjecture de Mordell. Publications Mathématiques de l’IHÉS, vol. 29 (1966), pp. 55–62 (French).Google Scholar