Research Article
Minimal complements for degrees below 0′
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 937-966
-
- Article
- Export citation
A structural investigation on formal topology: coreflection of formal covers and exponentiability
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 967-1005
-
- Article
- Export citation
Elimination theory for addition and the frobenius map in polynomial rings
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1006-1026
-
- Article
- Export citation
Higher-order semantics and extensionality
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1027-1088
-
- Article
- Export citation
Comparing DNR and WWKL
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1089-1104
-
- Article
- Export citation
A finite model-theoretical proof of a property of bounded query classes within PH
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1105-1116
-
- Article
- Export citation
Bounding prime models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1117-1142
-
- Article
- Export citation
The Mitchell order below rank-to-rank
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1143-1162
-
- Article
- Export citation
There is no SW-complete c.e. real
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1163-1170
-
- Article
- Export citation
Bi-coloured fields on the complex numbers
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1171-1186
-
- Article
- Export citation
Some model theory of sheaves of modules
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1187-1199
-
- Article
- Export citation
Generalized high degrees have the complementation property
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1200-1220
-
- Article
- Export citation
Coordinatisation by binding groups and unidimensionality in simple theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1221-1242
-
- Article
- Export citation
Local homogeneity
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1243-1260
-
- Article
- Export citation
More on regular reduced products
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1261-1266
-
- Article
- Export citation
Jonsson-like partition relations and j: V → V
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1267-1281
-
- Article
- Export citation
Front matter
JSL volume 69 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
JSL volume 69 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. b1-b9
-
- Article
-
- You have access
- Export citation



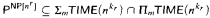
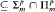 , then additionally
, then additionally 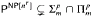 .
.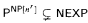 .
.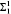 arity hierarchy to be strict over finite models.
arity hierarchy to be strict over finite models.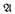 of
of 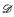 (≤
(≤ 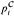 . A unidimensional simple theory eliminates the quantifier ∃
. A unidimensional simple theory eliminates the quantifier ∃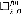 of the combinatorial principle
of the combinatorial principle 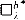 of [7]. the consistency of the failure, relative to the consistency of supercompact cardinals, of the following: for all regular filters
of [7]. the consistency of the failure, relative to the consistency of supercompact cardinals, of the following: for all regular filters 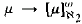 . We conclude with a discussion of some consistency questions concerning different versions of the axiom asserting the existence of a nontrivial elementary embedding
. We conclude with a discussion of some consistency questions concerning different versions of the axiom asserting the existence of a nontrivial elementary embedding