Article contents
Bounding prime models
Published online by Cambridge University Press: 12 March 2014
Abstract.
A set X is prime bounding if for every complete atomic decidable (CAD) theory T there is a prime model 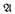 of T decidable in X. It is easy to see that X = 0′ is prime bounding. Denisov claimed that every X <T 0′ is not prime bounding, but we discovered this to be incorrect. Here we give the correct characterization that the prime bounding sets X ≤τ 0′ are exactly the sets which are not low2. Recall that X is low2 if X″ ≤τ 0″. To prove that a low2 set X is not prime bounding we use a 0′ -computable listing of the array of sets {Y : Y ≤τX } to build a CAD theory T which diagonalizes against all potential X-decidable prime models
of T decidable in X. It is easy to see that X = 0′ is prime bounding. Denisov claimed that every X <T 0′ is not prime bounding, but we discovered this to be incorrect. Here we give the correct characterization that the prime bounding sets X ≤τ 0′ are exactly the sets which are not low2. Recall that X is low2 if X″ ≤τ 0″. To prove that a low2 set X is not prime bounding we use a 0′ -computable listing of the array of sets {Y : Y ≤τX } to build a CAD theory T which diagonalizes against all potential X-decidable prime models 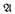 of T, To prove that any non-low2X is indeed prime bounding. we fix a function f ≤TX that is not dominated by a certain 0′-computable function that picks out generators of principal types. Given a CAD theory T. we use f to eventually find, for every formula φ(x̄) con sistent with T. a principal type which contains it. and hence to build an X-decidable prime model of T. We prove the prime bounding property equivalent to several other combinatorial properties, including some related to the limitwise monotonic functions which have been introduced elsewhere in computable model theory.
of T, To prove that any non-low2X is indeed prime bounding. we fix a function f ≤TX that is not dominated by a certain 0′-computable function that picks out generators of principal types. Given a CAD theory T. we use f to eventually find, for every formula φ(x̄) con sistent with T. a principal type which contains it. and hence to build an X-decidable prime model of T. We prove the prime bounding property equivalent to several other combinatorial properties, including some related to the limitwise monotonic functions which have been introduced elsewhere in computable model theory.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2004
References
REFERENCES
- 12
- Cited by




