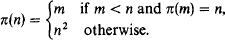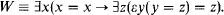Survey/expository paper
Classifying the computational complexity of problems
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1-43
-
- Article
- Export citation
Research Article
Prikry forcing at κ+ and beyond
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 44-50
-
- Article
- Export citation
No Jónsson filters over ℵω
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 51-53
-
- Article
- Export citation
Modules of existentially closed algebras
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 54-63
-
- Article
- Export citation
The reals in core models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 64-67
-
- Article
- Export citation
Relative lawlessness in intuitionistic analysis
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 68-88
-
- Article
- Export citation
Some consistency proofs and a characterization of inconsistency proofs in illative combinatory logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 89-110
-
- Article
- Export citation
Morasses and the Lévy-collapse
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 111-115
-
- Article
- Export citation
Elimination of quantifiers for ordered valuation rings
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 116-128
-
- Article
- Export citation
Remarks on weak notions of saturation in models of Peano arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 129-148
-
- Article
- Export citation
Concerning ultrafilters on ultrapowers
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 149-151
-
- Article
- Export citation
Definability in number fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 152-155
-
- Article
- Export citation
On Dedekind complete o-minimal structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 156-164
-
- Article
- Export citation
The degree of the set of sentences of predicate provability logic that are true under every interpretation1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 165-171
-
- Article
- Export citation
A constructive interpretation of the full set theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 172-201
-
- Article
- Export citation
Elementary axioms for canonical points of toposes
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 202-204
-
- Article
- Export citation
A strongly minimal expansion of (ω, s)
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 205-207
-
- Article
- Export citation
Simple r. e. degree structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 208-213
-
- Article
- Export citation
A note on a proof of Hilbert's second ε-theorem
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 214-215
-
- Article
- Export citation
Strong analogues of Martin's axiom Imply Axiom R
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 216-218
-
- Article
- Export citation



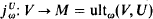 which will add a sequence
which will add a sequence 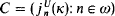 of indiscernibles for
of indiscernibles for 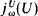 over
over 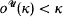 by Magidor [Mag], and his method readily extends to
by Magidor [Mag], and his method readily extends to 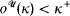 . In this case the measure
. In this case the measure 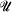 of measures and the set
of measures and the set 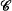 of indiscernibles for
of indiscernibles for 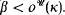 . The equivalence between forcing and iterated ultra-powers still holds true for such sequences: there is an interated ultrapower
. The equivalence between forcing and iterated ultra-powers still holds true for such sequences: there is an interated ultrapower 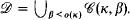 . That is, an indiscernible does not belong to a specific measure, but only to the whole sequence of measures on the cardinal
. That is, an indiscernible does not belong to a specific measure, but only to the whole sequence of measures on the cardinal 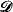 = ‹
= ‹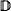 of lawlike sequences. For countable
of lawlike sequences. For countable  of sequences, generated by iterating definability over the continuum, is countable then the
of sequences, generated by iterating definability over the continuum, is countable then the 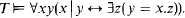
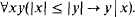
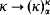 for all
for all 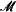 of
of 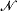 for some Dedekind complete model
for some Dedekind complete model 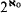 , then
, then 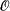 -minimal expansion of (
-minimal expansion of (