Hostname: page-component-848d4c4894-hfldf Total loading time: 0 Render date: 2024-05-08T05:53:14.646Z Has data issue: false hasContentIssue false
  • English
  • Français

Prikry forcing at κ+ and beyond

Published online by Cambridge University Press:  12 March 2014

William Mitchell
William Mitchell*
Affiliation:
Department of Mathematics, Pennsylvania State University, University Park, Pennsylvania 16802
Get access Rights & Permissions [Opens in a new window]

Extract

If U is a normal measure on κ then we can add indiscernibles for U either by Prikry forcing [P] or by taking an iterated ultrapower 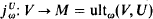which will add a sequence 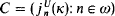of indiscernibles for 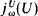over M. These constructions are equivalent: the set C of indiscernibles for 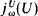added by the iterated ultrapower is Prikry generic for 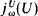[Mat]. Prikry forcing has been extended for sequences of measures of length 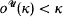by Magidor [Mag], and his method readily extends to 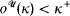. In this case the measure U is replaced by a sequence 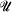of measures and the set C of indiscernibles is replaced by a system 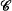of indiscernibles for 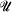: 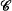is a function such that 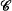(κ, β) is a set of indiscernibles for 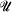(κ, β) for each 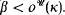. The equivalence between forcing and iterated ultra-powers still holds true for such sequences: there is an interated ultrapower j: V → M (which is defined in detail later in this paper) such that the system 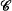of indiscernibles for j(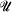) constructed by j is Magidor generic over M.

The construction of the system 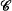of indiscernibles works equally well for o(κ) ≧ κ+. Radin has defined a variant of Prikry forcing which also works for o(κ) > κ+ ([R]; see also [Mi82] where Radin forcing is applied specifically to sequences of measures, rather than to hypermeasures as in Radin's paper), but Radin's forcing is weaker than Magidor's extension of Prikry forcing in the sense that the system 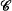of indiscernibles generated by the interated ultrapower is not Radin generic for j(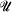), but only the set 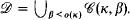. That is, an indiscernible does not belong to a specific measure, but only to the whole sequence of measures on the cardinal κ.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 52 , Issue 1 , March 1987 , pp. 44 - 50
Copyright
Copyright © Association for Symbolic Logic 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Mag] Magidor, M., Changing cofinality of cardinals, Fundamenta Mathematicae, vol. 99 (1978), pp. 61–71.CrossRefGoogle Scholar
[Mat] Mathias, A. R. D., On sequences generic in the sense of Prikry, Journal of the Australian Mathematical Society, vol. 15 (1973), pp. 409–414.CrossRefGoogle Scholar
[Mi82] Mitchell, W., How weak is a closed unbounded ultrafilter? Logic Colloquium '80 (van Dalen, D. et al., editors), North-Holland, Amsterdam, 1982, pp. 209–230.Google Scholar
[Mi84a] Mitchell, W., Indiscernibles, skies and ideals, Axiomatic set theory (Baumgartner, J. E. et al., editors), Contemporary Mathematics, vol. 31, American Mathematical Society, Providence, Rhode Island, 1984, pp. 161–182.CrossRefGoogle Scholar
[Mi84b] Mitchell, W., The core model for sequences of measures. I, Mathematical Proceedings of the Cambridge Philosophical Society, vol. 95 (1984), pp. 229–260.CrossRefGoogle Scholar
[Mi?] Mitchell, W., The core model for sequences of measures. II (to appear).Google Scholar
[P] Prikry, K., Changing measurable into accessible cardinals, Dissertationes Mathematicae (Rozprawy Matematyczne), vol. 68 (1970).Google Scholar
[R] Radin, L., Adding closed cofinal sequences to large cardinals, Annals of Mathematical Logic, vol. (1982), pp. 263–283.Google Scholar