Research Article
Local Kc constructions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 721-737
-
- Article
- Export citation
Which structural rules admit cut elimination? An algebraic criterion
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 738-754
-
- Article
- Export citation
On notions of genericity and mutual genericity
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 755-766
-
- Article
- Export citation
Models of non-well-founded sets via an indexed final coalgebra theorem
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 767-791
-
- Article
- Export citation
Reconstruction of homogeneous relational structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 792-802
-
- Article
- Export citation
An algebraic characterization of equivalent preferential models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 803-833
-
- Article
- Export citation
Substructural fuzzy logics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 834-864
-
- Article
- Export citation
Some results in polychromatic Ramsey theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 865-896
-
- Article
- Export citation
Erdős-Rado without choice
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 897-900
-
- Article
- Export citation
Turing computable embeddings
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 901-918
-
- Article
- Export citation
Characterizing rosy theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 919-940
-
- Article
- Export citation
Lower bounds for modal logics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 941-958
-
- Article
- Export citation
Approximate counting in bounded arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 959-993
-
- Article
- Export citation
Parallel interpolation, splitting, and relevance in belief change
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 994-1002
-
- Article
- Export citation
Π10 classes and strong degree spectra of relations
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1003-1018
-
- Article
- Export citation
DMP in strongly minimal sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1019-1030
-
- Article
- Export citation
Computable embeddings and strongly minimal theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1031-1040
-
- Article
- Export citation
Applications of Kolmogorov complexity to computable model theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1041-1054
-
- Article
- Export citation
The settling-time reducibility ordering
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1055-1071
-
- Article
- Export citation
A note on Σ1-maximal models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1072-1078
-
- Article
- Export citation



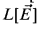 , then
, then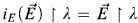 The natural proof only gives that if κ is Σ
The natural proof only gives that if κ is Σ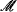 ) of an ω-categorical structure
) of an ω-categorical structure 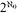 is open. This guarantees that the abstract group structure of Aut(
is open. This guarantees that the abstract group structure of Aut(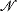 is ω-categorical with Aut(
is ω-categorical with Aut(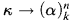 to mean “every colouring of
to mean “every colouring of 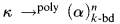 to mean “every
to mean “every 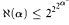 .
. subsets of 2
subsets of 2 -structure with a unique computable isomorphism type. In addition, using the construction we give an example of an ℵ
-structure with a unique computable isomorphism type. In addition, using the construction we give an example of an ℵ