Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-24T18:59:00.576Z Has data issue: false hasContentIssue false
  • English
  • Français

Applications of Kolmogorov complexity to computable model theory

Published online by Cambridge University Press:  12 March 2014

Bakhadyr Khoussainov ,
Pavel Semukhin  and
Frank Stephan
Bakhadyr Khoussainov
Affiliation:
Department of Computer Science, University of Auckland, Private Bag 92019, Auckland, New Zealand, E-mail: bmk@cs.auckland.ac.nz
Pavel Semukhin
Affiliation:
Department of Computer Science, University of Auckland, Private Bag 92019, Auckland, New Zealand, E-mail: pavel@cs.auckland.ac.nz
Frank Stephan
Affiliation:
National University of Singapore, Mathematical Institute, 2 Science Drive 2, Singapore117543, Republic of Singapore, E-mail:, fstephan@comp.nus.edu.sg
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we answer the following well-known open question in computable model theory. Does there exist a computable not ℵ0-categorical saturated structure with a unique computable isomor-phism type? Our answer is affirmative and uses a construction based on Kolmogorov complexity. With a variation of this construction, we also provide an example of an ℵ1-categorical but not ℵ0-categorical saturated 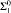-structure with a unique computable isomorphism type. In addition, using the construction we give an example of an ℵ1-categorical but not ℵ0-categorical theory whose only non-computable model is the prime one.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 72 , Issue 3 , September 2007 , pp. 1041 - 1054
Copyright
Copyright © Association for Symbolic Logic 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Calude, Cristian, Information and randomness: an algorithmic perspective, Springer, 2002.CrossRefGoogle Scholar
[2]Cholak, Peter, Shore, Richard, and Solomon, Reed, A computably stable structure with no Scott family of finitary formulas, Archive for Mathematical Logic, vol. 45 (2006), pp. 519–538.CrossRefGoogle Scholar
[3]Hirschfeldt, Denis, Khoussainov, Bakhadyr, and Semukhin, Pavel, An uncountably categorical theory whose only computably presentable model is saturated, Notre Dame Journal of Formal Logic, vol. 47 (2006), pp. 63–71.Google Scholar
[4]Hodges, Wilfrid, Model theory, Cambridge University Press, 1993.CrossRefGoogle Scholar
[5]Hodges, Wilfrid, A shorter model theory, Cambridge University Press, 1997.Google Scholar
[6]Khoussainov, Bakhadyr, Nies, André, and Shore, Richard, Computable models of theories with few models, Notre Dame Journal of Formal Logic, vol. 38 (1997), pp. 165–178.CrossRefGoogle Scholar
[7]Khoussainov, Bakhadyr and Shore, Richard, Computable isomorphisms, degree spectra of relations and Scott families, Annals of Pure and Applied Logic, vol. 91 (1999), pp. 1–15 and vol. 98 (1999), pp. 297–298.CrossRefGoogle Scholar
[8]Kudinov, Oleg V., An autostable 1-decidable model without a computable scott family of ∃-formulas, Algebra and Logic, vol. 35 (1996), pp. 255–260, English translation.CrossRefGoogle Scholar
[9]Li, Ming and Vitányi, Paul, An introduction to Kolmogorov complexity audits applications, Texts and Monographs in Computer Science, Springer, 1993.CrossRefGoogle Scholar
[10]Marker, David, Model theory: an introduction, Springer, 2002.Google Scholar
[11]Morley, Michael, Categoricity in power, Transactions of the American Mathematical Society, vol. 114 (1965), pp. 514–538.CrossRefGoogle Scholar
[12]Odifreddi, Piergiorgio, Classical recursion theory, North-Holland, 1989.Google Scholar
[13]Soare, Robert I., Recursively enumerable sets and degrees, Springer, 1987.CrossRefGoogle Scholar