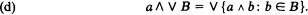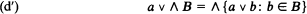Research Article
Strict-Π11 predicates on countable and cofinality ω transitive sets1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 161-173
-
- Article
- Export citation
An axiomatization for a class of two-cardinal models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 174-178
-
- Article
- Export citation
Definability of measures and ultrafilters
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 179-190
-
- Article
- Export citation
On deciding the provability of certain fixed point statements
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 191-193
-
- Article
- Export citation
Some models for intuitionistic finite type arithmetic with fan functional
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 194-202
-
- Article
- Export citation
On splitting stationary subsets of large cardinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 203-214
-
- Article
- Export citation
The consistency problem for NF
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 215-220
-
- Article
- Export citation
Fragments of first order logic, I: universal Horn logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 221-237
-
- Article
- Export citation
The use of Kripke's schema as a reduction principle
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 238-240
-
- Article
- Export citation
Sheaves and normal submodels
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 241-250
-
- Article
- Export citation
Theories with models of prescribed cardinalities1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 251-253
-
- Article
- Export citation
Minimal models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 254-260
-
- Article
- Export citation
Compactness and transfer for a fragment of L2
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 261-268
-
- Article
- Export citation
Craig interpolation theorem for intuitionistic logic and extensions Part III
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 269-271
-
- Article
- Export citation
Chang's conjecture and powers of singular cardinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 272-276
-
- Article
- Export citation
A model theoretic approach to Malcev conditions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 277-288
-
- Article
- Export citation
Definability in well quasi-ordered sets of structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 289-291
-
- Article
- Export citation
On Moschovakis closure ordinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 292-296
-
- Article
- Export citation
A lattice of interpretability types of theories1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 297-305
-
- Article
- Export citation
A new version of Beth semantics for intuitionistic logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 306-308
-
- Article
- Export citation



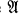 has type (κ, λ) if card(
has type (κ, λ) if card(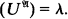 . Let
. Let 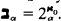

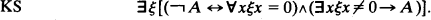
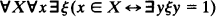
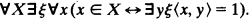
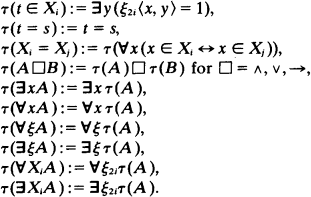
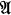 as a normal submodel of
as a normal submodel of 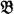 if
if 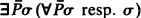 with σ in
with σ in 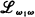 and
and 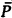 some string of predicate symbols. All languages considered are assumed to be countable. For each model
some string of predicate symbols. All languages considered are assumed to be countable. For each model 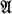 we shall define in a natural way its rank, denoted by rk (
we shall define in a natural way its rank, denoted by rk (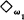 (cf. [3])
(cf. [3]) 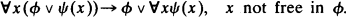
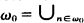 ,
, 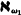 , is a strong limit cardinal, then
, is a strong limit cardinal, then 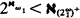 . They established similar bounds for powers of singular cardinals of cofinality greater than ω. Jech and Prikry in [3] showed that the Galvin-Hajnal bound can be improved if we assume that ω
. They established similar bounds for powers of singular cardinals of cofinality greater than ω. Jech and Prikry in [3] showed that the Galvin-Hajnal bound can be improved if we assume that ω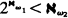 provided
provided 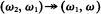
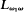 , but is introduced in a less specific context and accompanied by applications to
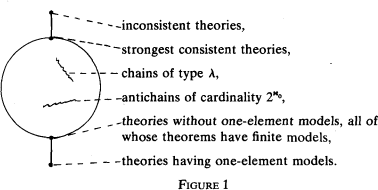
, but is introduced in a less specific context and accompanied by applications to 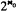 such types and they are partially ordered by the relation of local interpretability. This partial ordering is of lattice type and has the following form:
such types and they are partially ordered by the relation of local interpretability. This partial ordering is of lattice type and has the following form: