Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-24T17:27:41.186Z Has data issue: false hasContentIssue false
  • English
  • Français

Craig interpolation theorem for intuitionistic logic and extensions Part III

Published online by Cambridge University Press:  12 March 2014

Dov M. Gabbay
Dov M. Gabbay*
Affiliation:
Bar-Ilan University, Ramat-Gan, Israel
Get access Rights & Permissions [Opens in a new window]

Extract

This is a continuation of two previous papers by the same title [2] and examines mainly the interpolation property for the logic CD with constant domains, i.e., the extension of the intuitionistic predicate logic with the schema

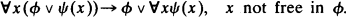
It is known [3], [4] that this logic is complete for the class of all Kripke structures with constant domains.

Theorem 47. The strong Robinson consistency theorem is not true for CD.

Proof. Consider the following Kripke structure with constant domains. The set S of possible worlds is ω0, the set of positive integers. R is the natural ordering ≤. Let ω0 0 = 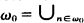, Bn, is a sequence of pairwise disjoint infinite sets. Let L0 be a language with the unary predicates P, P1 and consider the following extensions for P,P1 at the world m.

(a) P is true on ⋃i≤2nBi, and P1 is true on ⋃i≤2n+1Bi for m = 2n.

(b) P is true on ⋃i≤2nBi, and P1 for ⋃i≤2n+1Bi for m = 2n.

Let (Δ,Θ) be the complete theory of this structure. Consider another unary predicate Q. Let L be the language with P, Q and let M be the language with P1, Q.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 42 , Issue 2 , June 1977 , pp. 269 - 271
Copyright
Copyright © Association for Symbolic Logic 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Gabbay, D., Model theory for intuitionistic logic. I, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 18 (1972), pp. 49–54.Google Scholar
[2]Gabbay, D., Craig interpolation theorem for intuitionistic logic and extensions. I, II, Logic Colloquium '69 (Gandy, R., Editor), North-Holland, Amsterdam.Google Scholar
[3]Gabbay, D., On 2nd order intuitionistic propositional calculus with full comprehension, Archiv für Mathematische Logik, vol. 16 (1974), pp. 177–186.Google Scholar
[4]Gornemann, S., A logic stronger than intuitionism, this Journal, vol. 36 (1971), pp. 249–262.Google Scholar
[5]Bowen, K. A., Normal modal model theory, Journal of Philosophical Logic, vol. 4 (1975), pp. 97–131.CrossRefGoogle Scholar