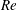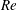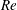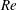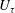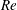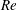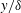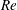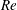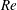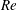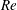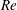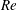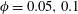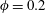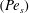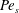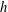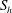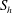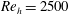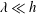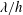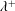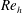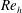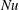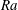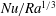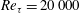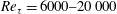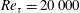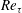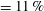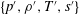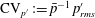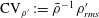JFM Papers
Can a turbulent boundary layer become independent of the Reynolds number?
-
- Published online by Cambridge University Press:
- 18 July 2018, pp. 1-22
-
- Article
- Export citation
Computational modelling and analysis of haemodynamics in a simple model of aortic stenosis
-
- Published online by Cambridge University Press:
- 19 July 2018, pp. 23-49
-
- Article
- Export citation
The role of the seam in the swing of a cricket ball
-
- Published online by Cambridge University Press:
- 19 July 2018, pp. 50-82
-
- Article
- Export citation
Importance of the nozzle-exit boundary-layer state in subsonic turbulent jets
-
- Published online by Cambridge University Press:
- 19 July 2018, pp. 83-124
-
- Article
- Export citation
Quantification of turbulent mixing in colliding gravity currents
-
- Published online by Cambridge University Press:
- 19 July 2018, pp. 125-147
-
- Article
- Export citation
Suspensions of finite-size neutrally buoyant spheres in turbulent duct flow
-
- Published online by Cambridge University Press:
- 19 July 2018, pp. 148-186
-
- Article
- Export citation
Locomotion inside a surfactant-laden drop at low surface Péclet numbers
-
- Published online by Cambridge University Press:
- 19 July 2018, pp. 187-230
-
- Article
- Export citation
The lifetimes of evaporating sessile droplets are significantly extended by strong thermal effects
-
- Published online by Cambridge University Press:
- 19 July 2018, pp. 231-244
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Plane blast wave interaction with an elongated straight and inclined heat-generated inhomogeneity
-
- Published online by Cambridge University Press:
- 19 July 2018, pp. 245-267
-
- Article
- Export citation
On the spatial segregation of helicity by inertial waves in dynamo simulations and planetary cores
-
- Published online by Cambridge University Press:
- 19 July 2018, pp. 268-287
-
- Article
- Export citation
Secondary flow in spanwise-periodic in-phase sinusoidal channels
-
- Published online by Cambridge University Press:
- 19 July 2018, pp. 288-316
-
- Article
- Export citation
Flow-induced vibration of D-section cylinders: an afterbody is not essential for vortex-induced vibration
-
- Published online by Cambridge University Press:
- 20 July 2018, pp. 317-343
-
- Article
- Export citation
Unsteady thrust, lift and moment of a two-dimensional flapping thin airfoil in the presence of leading-edge vortices: a first approximation from linear potential theory
-
- Published online by Cambridge University Press:
- 20 July 2018, pp. 344-373
-
- Article
- Export citation
Bulk temperature and heat transport in turbulent Rayleigh–Bénard convection of fluids with temperature-dependent properties
-
- Published online by Cambridge University Press:
- 20 July 2018, pp. 374-390
-
- Article
- Export citation
Fully resolved measurements of turbulent boundary layer flows up to
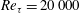 $Re_{\unicode[STIX]{x1D70F}}=20\,000$
$Re_{\unicode[STIX]{x1D70F}}=20\,000$
-
- Published online by Cambridge University Press:
- 20 July 2018, pp. 391-415
-
- Article
- Export citation
Robust features of a turbulent boundary layer subjected to high-intensity free-stream turbulence
-
- Published online by Cambridge University Press:
- 20 July 2018, pp. 416-435
-
- Article
- Export citation
The influence of wall roughness on bubble drag reduction in Taylor–Couette turbulence
-
- Published online by Cambridge University Press:
- 20 July 2018, pp. 436-446
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Correlation coefficients of thermodynamic fluctuations in compressible aerodynamic turbulence
-
- Published online by Cambridge University Press:
- 25 July 2018, pp. 447-478
-
- Article
- Export citation
Wall pressure and vorticity in the intermittently turbulent regime of the Stokes boundary layer
-
- Published online by Cambridge University Press:
- 25 July 2018, pp. 479-506
-
- Article
- Export citation
Axisymmetric three-dimensional gravity currents generated by lock exchange
-
- Published online by Cambridge University Press:
- 25 July 2018, pp. 507-544
-
- Article
-
- You have access
- Open access
- HTML
- Export citation