Article contents
Secondary flow in spanwise-periodic in-phase sinusoidal channels
Published online by Cambridge University Press: 19 July 2018
Abstract
Direct numerical simulations (DNSs) are performed to analyse the secondary flow of Prandtl’s second kind in fully developed spanwise-periodic channels with in-plane sinusoidal walls. The secondary flow is characterized for different combinations of wave parameters defining the wall geometry at 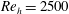 $Re_{h}=2500$ and 5000, where
$Re_{h}=2500$ and 5000, where 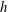 $h$ is the half-height of the channel. The total cross-flow rate in the channel
$h$ is the half-height of the channel. The total cross-flow rate in the channel 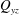 $Q_{yz}$ is defined along with a theoretical model to predict its behaviour. Interaction between the secondary flows from opposite walls is observed if
$Q_{yz}$ is defined along with a theoretical model to predict its behaviour. Interaction between the secondary flows from opposite walls is observed if 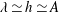 $\unicode[STIX]{x1D706}\simeq h\simeq A$, where
$\unicode[STIX]{x1D706}\simeq h\simeq A$, where 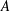 $A$ and
$A$ and 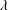 $\unicode[STIX]{x1D706}$ are the amplitude and wavelength of the sinusoidal function defining the wall geometry. As the outer-scaled wavelength (
$\unicode[STIX]{x1D706}$ are the amplitude and wavelength of the sinusoidal function defining the wall geometry. As the outer-scaled wavelength (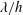 $\unicode[STIX]{x1D706}/h$) is reduced, the secondary vortices become smaller and faster, increasing the total cross-flow rate per wall. However, if the inner-scaled wavelength (
$\unicode[STIX]{x1D706}/h$) is reduced, the secondary vortices become smaller and faster, increasing the total cross-flow rate per wall. However, if the inner-scaled wavelength (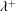 $\unicode[STIX]{x1D706}^{+}$) is below 130 viscous units, the cross-flow decays for smaller wavelengths. By analysing cases in which the wavelength of the wall is much smaller than the half-height of the channel
$\unicode[STIX]{x1D706}^{+}$) is below 130 viscous units, the cross-flow decays for smaller wavelengths. By analysing cases in which the wavelength of the wall is much smaller than the half-height of the channel 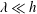 $\unicode[STIX]{x1D706}\ll h$, we show that the cross-flow distribution depends almost entirely on the separation between the scales of the instantaneous vortices, where the upper and lower bounds are determined by
$\unicode[STIX]{x1D706}\ll h$, we show that the cross-flow distribution depends almost entirely on the separation between the scales of the instantaneous vortices, where the upper and lower bounds are determined by 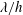 $\unicode[STIX]{x1D706}/h$ and
$\unicode[STIX]{x1D706}/h$ and 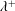 $\unicode[STIX]{x1D706}^{+}$, respectively. Therefore, the distribution of the secondary flow relative to the size of the wave at a given
$\unicode[STIX]{x1D706}^{+}$, respectively. Therefore, the distribution of the secondary flow relative to the size of the wave at a given 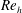 $Re_{h}$ can be replicated at higher
$Re_{h}$ can be replicated at higher 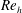 $Re_{h}$ by decreasing
$Re_{h}$ by decreasing 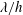 $\unicode[STIX]{x1D706}/h$ and keeping
$\unicode[STIX]{x1D706}/h$ and keeping 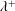 $\unicode[STIX]{x1D706}^{+}$ constant. The mechanisms that contribute to the mean cross-flow are analysed in terms of the Reynolds stresses and using quadrant analysis to evaluate the probability density function of the bursting events. These events are further classified with respect to the sign of their instantaneous spanwise velocities. Sweeping events and ejections are preferentially located in the valleys and peaks of the wall, respectively. The sweeps direct the instantaneous cross-flow from the core of the channel towards the wall, turning in the wall-tangent direction towards the peaks. The ejections drive the instantaneous cross-flow from the near-wall region towards the core. This preferential behaviour is identified as one of the main contributors to the secondary flow.
$\unicode[STIX]{x1D706}^{+}$ constant. The mechanisms that contribute to the mean cross-flow are analysed in terms of the Reynolds stresses and using quadrant analysis to evaluate the probability density function of the bursting events. These events are further classified with respect to the sign of their instantaneous spanwise velocities. Sweeping events and ejections are preferentially located in the valleys and peaks of the wall, respectively. The sweeps direct the instantaneous cross-flow from the core of the channel towards the wall, turning in the wall-tangent direction towards the peaks. The ejections drive the instantaneous cross-flow from the near-wall region towards the core. This preferential behaviour is identified as one of the main contributors to the secondary flow.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 16
- Cited by





