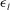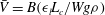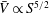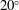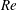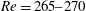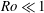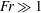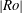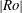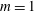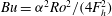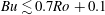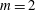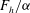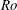Papers
On the peculiar structure of a helical wake vortex behind an inclined prolate spheroid
-
- Published online by Cambridge University Press:
- 19 July 2016, pp. 1-12
-
- Article
- Export citation
Dispersion controlled by permeable surfaces: surface properties and scaling
-
- Published online by Cambridge University Press:
- 19 July 2016, pp. 13-42
-
- Article
- Export citation
Data-enabled prediction of streak breakdown in pressure-gradient boundary layers
-
- Published online by Cambridge University Press:
- 19 July 2016, pp. 43-64
-
- Article
- Export citation
Propagation of viscous currents on a porous substrate with finite capillary entry pressure
-
- Published online by Cambridge University Press:
- 19 July 2016, pp. 65-90
-
- Article
- Export citation
Air entrainment and bubble statistics in breaking waves
-
- Published online by Cambridge University Press:
- 19 July 2016, pp. 91-129
-
- Article
- Export citation
Neutralization of a spray of electrically charged droplets by a corona discharge
-
- Published online by Cambridge University Press:
- 19 July 2016, pp. 130-149
-
- Article
- Export citation
Numerical study of viscous starting flow past wedges
-
- Published online by Cambridge University Press:
- 19 July 2016, pp. 150-165
-
- Article
- Export citation
A two-phase two-layer model for fluidized granular flows with dilatancy effects
-
- Published online by Cambridge University Press:
- 19 July 2016, pp. 166-221
-
- Article
- Export citation
A vortex force study for a flat plate at high angle of attack
-
- Published online by Cambridge University Press:
- 19 July 2016, pp. 222-249
-
- Article
- Export citation
Holes stabilize freely falling coins
-
- Published online by Cambridge University Press:
- 21 July 2016, pp. 250-259
-
- Article
- Export citation
Kinematics of fluid particles on the sea surface: Hamiltonian theory
-
- Published online by Cambridge University Press:
- 21 July 2016, pp. 260-288
-
- Article
- Export citation
Numerical investigation of the role of free-stream turbulence in boundary-layer separation
-
- Published online by Cambridge University Press:
- 21 July 2016, pp. 289-321
-
- Article
- Export citation
Front dynamics and entrainment of finite circular gravity currents on an unbounded uniform slope
-
- Published online by Cambridge University Press:
- 21 July 2016, pp. 322-352
-
- Article
- Export citation
Three-dimensional direct numerical simulation of wake transitions of a circular cylinder
-
- Published online by Cambridge University Press:
- 25 July 2016, pp. 353-391
-
- Article
- Export citation
Viscoelastic shear flow over a wavy surface
-
- Published online by Cambridge University Press:
- 25 July 2016, pp. 392-429
-
- Article
- Export citation
Investigations of non-hydrostatic, stably stratified and rapidly rotating flows
-
- Published online by Cambridge University Press:
- 25 July 2016, pp. 430-458
-
- Article
- Export citation
A scaling law for the shear-production range of second-order structure functions
-
- Published online by Cambridge University Press:
- 25 July 2016, pp. 459-474
-
- Article
- Export citation
The wake of two staggered square cylinders
-
- Published online by Cambridge University Press:
- 25 July 2016, pp. 475-507
-
- Article
- Export citation
Stability of an isolated pancake vortex in continuously stratified-rotating fluids
-
- Published online by Cambridge University Press:
- 25 July 2016, pp. 508-553
-
- Article
- Export citation
Properties of the turbulent/non-turbulent interface in boundary layers
-
- Published online by Cambridge University Press:
- 26 July 2016, pp. 554-596
-
- Article
- Export citation