Hostname: page-component-76fb5796d-zzh7m Total loading time: 0 Render date: 2024-04-26T22:50:36.120Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensional direct numerical simulation of wake transitions of a circular cylinder

Published online by Cambridge University Press:  25 July 2016

Hongyi Jiang ,
Liang Cheng ,
Scott Draper ,
Hongwei An  and
Feifei Tong
Hongyi Jiang*
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
Liang Cheng
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China
Scott Draper
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia Centre for Offshore Foundation Systems, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
Hongwei An
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
Feifei Tong
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
*
†Email address for correspondence: hongyijiang88@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

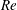This paper presents three-dimensional (3D) direct numerical simulations (DNS) of flow past a circular cylinder over a range of Reynolds number ($Re$) up to 300. The gradual wake transition process from mode A* (i.e. mode A with large-scale vortex dislocations) to mode B is well captured over a range of 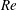$Re$ from 230 to 260. The mode swapping process is investigated in detail with the aid of numerical flow visualization. It is found that the mode B structures in the transition process are developed based on the streamwise vortices of mode A or A* which destabilize the braid shear layer region. For each case within the transition range, the transient mode swapping process consists of dislocation and non-dislocation cycles. With the increase of 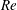$Re$, it becomes more difficult to trigger dislocations from the pure mode A structure and form a dislocation cycle, and each dislocation stage becomes shorter in duration, resulting in a continuous decrease in the probability of occurrence of mode A* and a continuous increase in the probability of occurrence of mode B. The occurrence of mode A* results in a relatively strong flow three-dimensionality. A critical condition is confirmed at approximately 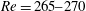$Re=265{-}270$, where the weakest flow three-dimensionality is observed, marking a transition from the disappearance of mode A* to the emergence of increasingly disordered mode B structures.

JFM classification

Vortex Flows: Vortex instability Wakes/Jets: Vortex streets Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 801 , 25 August 2016 , pp. 353 - 391
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
Barkley, D., Tuckerman, L. S. & Golubitsky, M. 2000 Bifurcation theory for three-dimensional flow in the wake of a circular cylinder. Phys. Rev. E 61, 5247–5252.CrossRefGoogle ScholarPubMed
Behara, S. & Mittal, S. 2010 Wake transition in flow past a circular cylinder. Phys. Fluids 22, 114104.CrossRefGoogle Scholar
Braza, M., Faghani, D. & Persillon, H. 2001 Successive stages and the role of natural vortex dislocations in three-dimensional wake transition. J. Fluid Mech. 439, 1–41.Google Scholar
Hammache, M. & Gharib, M. 1991 An experimental study of the parallel and oblique vortex shedding from circular cylinders. J. Fluid Mech. 232, 567–590.Google Scholar
Henderson, R. D. 1997 Nonlinear dynamics and pattern formation in turbulent wake transition. J. Fluid Mech. 352, 65–112.Google Scholar
Issa, R. I. 1986 Solution of implicitly discretized fluid flow equations by operator-splitting. J. Comput. Phys. 62, 40–65.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Leweke, T. & Williamson, C. H. K. 1998 Three-dimensional instabilities in wake transition. Eur. J. Mech. (B/Fluids) 17, 571–586.Google Scholar
Miller, G. D. & Williamson, C. H. K. 1994 Control of three-dimensional phase dynamics in a cylinder wake. Exp. Fluids 18, 26–35.Google Scholar
Norberg, C. 1994 An experimental investigation of the flow around a circular cylinder: influence of aspect ratio. J. Fluid Mech. 258, 287–316.Google Scholar
OpenFOAM. Available from www.openfoam.org.Google Scholar
Posdziech, O. & Grundmann, R. 2001 Numerical simulation of the flow around an infinitely long circular cylinder in the transition regime. Theor. Comput. Fluid Dyn. 15, 121–141.Google Scholar
Prasad, A. & Williamson, C. H. K. 1997 Three-dimensional effects in turbulent bluff-body wakes. J. Fluid Mech. 343, 235–265.CrossRefGoogle Scholar
Rao, A., Thompson, M. C., Leweke, T. & Hourigan, K. 2013 The flow past a circular cylinder translating at different heights above a wall. J. Fluids Struct. 41, 9–21.CrossRefGoogle Scholar
Roshko, A.1954 On the development of turbulent wakes from vortex streets. NACA Rep. 1191.Google Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2003 A coupled Landau model describing the Strouhal–Reynolds number profile of a three-dimensional circular cylinder wake. Phys. Fluids 15, L68–L71.Google Scholar
Thompson, M. C., Leweke, T. & Williamson, C. H. K. 2001 The physical mechanism of transition in bluff body wakes. J. Fluids Struct. 15, 607–616.CrossRefGoogle Scholar
Tritton, D. J. 1959 Experiments on the flow past a circular cylinder at low Reynolds numbers. J. Fluid Mech. 6, 547–567.CrossRefGoogle Scholar
Williamson, C. H. K. 1988 The existence of two stages in the transition to three-dimensionality of a cylinder wake. Phys. Fluids 31, 3165–3168.Google Scholar
Williamson, C. H. K. 1989 Oblique and parallel modes of vortex shedding in the wake of a circular cylinder at low Reynolds numbers. J. Fluid Mech. 206, 579–627.Google Scholar
Williamson, C. H. K. 1996a Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.Google Scholar
Williamson, C. H. K. 1996b Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.Google Scholar
Williamson, C. H. K. & Roshko, A. 1990 Measurements of base pressure in the wake of a cylinder at low Reynolds numbers. Z. Flugwiss. Weltraumforsch. 14, 38–46.Google Scholar