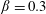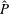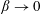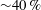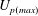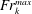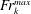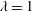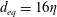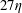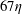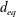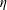Papers
Reduced-order analysis of buffet flow of space launchers
-
- Published online by Cambridge University Press:
- 14 February 2017, pp. 1-25
-
- Article
- Export citation
Separations and secondary structures due to unsteady flow in a curved pipe
-
- Published online by Cambridge University Press:
- 14 February 2017, pp. 26-59
-
- Article
- Export citation
An impulse-based approach to estimating forces in unsteady flow
-
- Published online by Cambridge University Press:
- 14 February 2017, pp. 60-76
-
- Article
- Export citation
Multiple solutions for granular flow over a smooth two-dimensional bump
-
- Published online by Cambridge University Press:
- 15 February 2017, pp. 77-116
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the genesis and evolution of barchan dunes: morphodynamics
-
- Published online by Cambridge University Press:
- 15 February 2017, pp. 117-148
-
- Article
- Export citation
Marginally stable and turbulent boundary layers in low-curvature Taylor–Couette flow
-
- Published online by Cambridge University Press:
- 15 February 2017, pp. 149-168
-
- Article
- Export citation
Local versus volume-integrated turbulence and mixing in breaking internal waves on slopes
-
- Published online by Cambridge University Press:
- 17 February 2017, pp. 169-198
-
- Article
- Export citation
Rotational kinematics of large cylindrical particles in turbulence
-
- Published online by Cambridge University Press:
- 20 February 2017, pp. 199-222
-
- Article
- Export citation
Evolution of the velocity gradient tensor invariant dynamics in a turbulent boundary layer
-
- Published online by Cambridge University Press:
- 20 February 2017, pp. 223-242
-
- Article
- Export citation
Stability, intermittency and universal Thorpe length distribution in a laboratory turbulent stratified shear flow
-
- Published online by Cambridge University Press:
- 21 February 2017, pp. 243-256
-
- Article
- Export citation
Vortex breakdown, linear global instability and sensitivity of pipe bifurcation flows
-
- Published online by Cambridge University Press:
- 20 February 2017, pp. 257-294
-
- Article
- Export citation
Genesis and evolution of velocity gradients in near-field spatially developing turbulence
-
- Published online by Cambridge University Press:
- 20 February 2017, pp. 295-332
-
- Article
- Export citation
Large-scale-vortex dynamos in planar rotating convection
-
- Published online by Cambridge University Press:
- 20 February 2017, pp. 333-360
-
- Article
- Export citation
Anisotropic Helmholtz and wave–vortex decomposition of one-dimensional spectra
-
- Published online by Cambridge University Press:
- 21 February 2017, pp. 361-387
-
- Article
- Export citation
On steady non-breaking downstream waves and the wave resistance – Stokes’ method
-
- Published online by Cambridge University Press:
- 20 February 2017, pp. 388-414
-
- Article
- Export citation
Lissajous trajectories in electromagnetically driven vortices
-
- Published online by Cambridge University Press:
- 21 February 2017, pp. 415-434
-
- Article
- Export citation
Linear and nonlinear dynamics of pulsatile channel flow
-
- Published online by Cambridge University Press:
- 21 February 2017, pp. 435-480
-
- Article
- Export citation
Shore protection by oblique seabed bars
-
- Published online by Cambridge University Press:
- 21 February 2017, pp. 481-510
-
- Article
- Export citation
Direct numerical simulations of a high Karlovitz number laboratory premixed jet flame – an analysis of flame stretch and flame thickening
-
- Published online by Cambridge University Press:
- 23 February 2017, pp. 511-536
-
- Article
- Export citation
Natural convection in a corrugated slot
-
- Published online by Cambridge University Press:
- 23 February 2017, pp. 537-569
-
- Article
- Export citation