Article contents
Stability, intermittency and universal Thorpe length distribution in a laboratory turbulent stratified shear flow
Published online by Cambridge University Press: 21 February 2017
Abstract
Stratified shear flows occur in many geophysical contexts, from oceanic overflows and river estuaries to wind-driven thermocline layers. We explore a turbulent wall-bounded shear flow of lighter miscible fluid into a quiescent fluid of higher density with a range of Richardson numbers 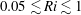 $0.05\lesssim Ri\lesssim 1$. In order to find a stability parameter that allows close comparison with linear theory and with idealized experiments and numerics, we investigate different definitions of
$0.05\lesssim Ri\lesssim 1$. In order to find a stability parameter that allows close comparison with linear theory and with idealized experiments and numerics, we investigate different definitions of 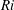 $Ri$. We find that a gradient Richardson number defined on fluid interface sections where there is no overturning at or adjacent to the maximum density gradient position provides an excellent stability parameter, which captures the Miles–Howard linear stability criterion. For small
$Ri$. We find that a gradient Richardson number defined on fluid interface sections where there is no overturning at or adjacent to the maximum density gradient position provides an excellent stability parameter, which captures the Miles–Howard linear stability criterion. For small 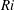 $Ri$ the flow exhibits robust Kelvin–Helmholtz instability, whereas for larger
$Ri$ the flow exhibits robust Kelvin–Helmholtz instability, whereas for larger 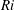 $Ri$ interfacial overturning is more intermittent with less frequent Kelvin–Helmholtz events and emerging Holmboe wave instability consistent with a thicker velocity layer compared with the density layer. We compute the perturbed fraction of interface as a quantitative measure of the flow intermittency, which is approximately 1 for the smallest
$Ri$ interfacial overturning is more intermittent with less frequent Kelvin–Helmholtz events and emerging Holmboe wave instability consistent with a thicker velocity layer compared with the density layer. We compute the perturbed fraction of interface as a quantitative measure of the flow intermittency, which is approximately 1 for the smallest 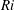 $Ri$ but decreases rapidly as
$Ri$ but decreases rapidly as 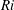 $Ri$ increases, consistent with linear theory. For the perturbed regions, we use the Thorpe scale to characterize the overturning properties of these flows. The probability distribution of the non-zero Thorpe length yields a universal exponential form, suggesting that much of the overturning results from increasingly intermittent Kelvin–Helmholtz instability events. The distribution of turbulent kinetic energy, conditioned on the intermittency fraction, has a similar form, suggesting an explanation for the universal scaling collapse of the Thorpe length distribution.
$Ri$ increases, consistent with linear theory. For the perturbed regions, we use the Thorpe scale to characterize the overturning properties of these flows. The probability distribution of the non-zero Thorpe length yields a universal exponential form, suggesting that much of the overturning results from increasingly intermittent Kelvin–Helmholtz instability events. The distribution of turbulent kinetic energy, conditioned on the intermittency fraction, has a similar form, suggesting an explanation for the universal scaling collapse of the Thorpe length distribution.
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 5
- Cited by



