Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-24T23:19:05.364Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortex breakdown, linear global instability and sensitivity of pipe bifurcation flows

Published online by Cambridge University Press:  20 February 2017

Kevin K. Chen Open the ORCID record for Kevin K. Chen [Opens in a new window] ,
Clarence W. Rowley  and
Howard A. Stone
Kevin K. Chen
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Clarence W. Rowley
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Howard A. Stone
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

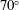Pipe bifurcations are common flow configurations in both natural and man-made systems. This study follows our previous report (Chen et al., Phys. Fluids, vol. 27, 2015, 034107) by describing three aspects of flows through junction angles of $70^{\circ }$, 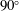$90^{\circ }$ and 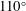$110^{\circ }$, with a square cross-section. First, the inflow creates tightly spiralling vortices in four quadrants of the junction. For sufficiently large Reynolds number 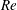$Re$, these vortices undergo behaviour resembling steady near-axisymmetric breakdown. With increasing 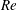$Re$, the flow through the 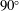$90^{\circ }$ junction remains steady and stable until the first Hopf bifurcation. Beyond the Hopf bifurcation, the vortices undergo a helical instability. The 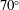$70^{\circ }$ and 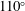$110^{\circ }$ junctions, however, first exhibit pitchfork bifurcations leading to asymmetric solutions. Second, the direct eigenmodes of the linearised flow are large in vortices in the outlet pipes, whereas the adjoint eigenmodes primarily reside in a small region in the inlet and the junction, near the front and back walls. Third, the sensitivities of the eigenvalues to spatially localised feedback and base flow modifications are greatest in and near the junction vortices. We highlight the regions of high growth rate and frequency sensitivity, as well as regions where the production and transport of perturbations by modifications of the base flow contribute most to the base flow sensitivity. The flow separation at the corners of the junction does not coincide with the eigenmodes or sensitivity regions.

JFM classification

Instability: Instability Vortex Flows: Vortex breakdown Vortex Flows: Vortex Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 815 , 25 March 2017 , pp. 257 - 294
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahnert, T. & Baerwolff, G. 2014 Numerical comparison of hybridized discontinuous Galerkin and finite volume methods for incompressible flow. Intl J. Numer. Meth. Fluids 76, 267–281.Google Scholar
Åkervik, E., Hœpffner, J., Ehrenstein, U. & Henningson, D. S. 2007 Optimal growth, model reduction and control in a separated boundary-layer flow using global eigenmodes. J. Fluid Mech. 579, 305–314.Google Scholar
Armijo, L. 1966 Minimization of functions having Lipschitz continuous first partial derivatives. Pac. J. Maths 16, 1–3.Google Scholar
Ault, J. T., Chen, K. K. & Stone, H. A. 2015 Downstream decay of fully developed Dean flow. J. Fluid Mech. 777, 219–244.Google Scholar
Ault, J. T., Fani, A., Chen, K. K., Shin, S., Gallaire, F. & Stone, H. A. 2016 Vortex-breakdown-induced particle capture in branching junctions. Phys. Rev. Lett. 117, 084501.Google Scholar
Bagheri, S., Brandt, L. & Henningson, D. S. 2009 Input–output analysis, model reduction and control of the flat-plate boundary layer. J. Fluid Mech. 620, 263–298.Google Scholar
Batchelor, G. K. 1964 Axial flow in trailing line vortices. J. Fluid Mech. 20, 645–658.Google Scholar
Bothe, D., Stemich, C. & Warnecke, H.-J. 2006 Fluid mixing in a T-shaped micro-mixer. Chem. Engng Sci. 61, 2950–2958.Google Scholar
Bottaro, A., Corbett, P. & Luchini, P. 2003 The effect of base flow variation on flow stability. J. Fluid Mech. 476, 293–302.Google Scholar
Brown, G. L. & Lopez, J. M. 1990 Axisymmetric vortex breakdown. Part 2. Physical mechanisms. J. Fluid Mech. 221, 553–576.Google Scholar
Chakraborty, P., Balachandar, S. & Adrian, R. J. 2005 On the relationships between local vortex identification schemes. J. Fluid Mech. 535, 189–214.Google Scholar
Chandler, G. J., Juniper, M. P., Nichols, J. W. & Schmid, P. J. 2012 Adjoint algorithms for the Navier–Stokes equations in the low Mach number limit.. J. Comput. Phys. 231, 1900–1916.Google Scholar
Chen, K. K., Rowley, C. W. & Stone, H. A. 2015 Vortex dynamics in a pipe T-junction: recirculation and sensitivity. Phys. Fluids 27, 034107.Google Scholar
Chomaz, J.-M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.Google Scholar
Crow, S. C. 1970 Stability theory for a pair of trailing vortices. AIAA J. 8, 2172–2179.Google Scholar
Doorly, D. & Sherwin, S. 2009 Cardiovascular Mathematics, Modeling, Simulation and Applications, vol. 1. chap. 5. Springer.Google Scholar
Dreher, S., Kockmann, N. & Woias, P. 2009 Characterization of laminar transient flow regimes and mixing in T-shaped micromixers. Heat Transfer Engng 30, 91–100.Google Scholar
Eloy, C. & Le Dizès, S. 1999 Three-dimensional instability of Burgers and Lamb–Oseen vortices in a strain field. J. Fluid Mech. 378, 145–166.Google Scholar
Engler, M., Kockmann, N., Kiefer, T. & Woias, P. 2004 Numerical and experimental investigations on liquid mixing in static micromixers. Chem. Engng J. 101, 315–322.Google Scholar
Fani, A., Camarri, S. & Salvetti, M. V. 2013 Investigation of the steady engulfment regime in a three-dimensional T-mixer. Phys. Fluids 25, 064102.Google Scholar
Ferziger, J. H. & Perić, M. 2002 Computational Methods for Fluid Dynamics, 3rd edn. Springer.Google Scholar
Franklin, G. F., Powell, J. D. & Emami-Naeini, A. 2010 Feedback Control of Dynamic Systems, 6th edn. Prentice Hall.Google Scholar
Gallaire, F. O., Ruith, M., Meiburg, E., Chomaz, J.-M. & Huerre, P. 2006 Spiral vortex breakdown as a global mode. J. Fluid Mech. 549, 71–80.Google Scholar
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.Google Scholar
Gresho, P. M. & Sani, R. L. 1987 On pressure boundary conditions for the incompressible Navier–Stokes equations. Intl J. Numer. Meth. Fluids 7, 1111–1145.Google Scholar
Guckenheimer, J. & Holmes, P. 1983 Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, Applied Mathematical Sciences, vol. 42. Springer.Google Scholar
Hall, M. G. 1972 Vortex breakdown. Annu. Rev. Fluid Mech. 4, 195–218.Google Scholar
Haller, D., Woias, P. & Kockmann, N. 2009 Simulation and experimental investigation of pressure loss and heat transfer in microchannel networks containing bends and T-junctions. Intl J. Heat Mass Transfer 52, 2678–2689.Google Scholar
Haller, G. 2005 An objective definition of a vortex. J. Fluid Mech. 525, 1–26.Google Scholar
Haward, S. J., Poole, R. J., Alves, M. A., Oliveira, P. J., Goldenfeld, N. & Shen, A. Q. 2016 Tricritical spiral vortex instability in cross-slot flow. Phys. Rev. E 93, 031101.Google Scholar
Heaton, C. J., Nichols, J. W. & Schmid, P. J. 2009 Global linear stability of the non-parallel Batchelor vortex. J. Fluid Mech. 629, 139–160.Google Scholar
Hill, D. C. 1992 A theoretical approach for analyzing the restabilization of wakes. In 30th AIAA Aerospace Sciences Meeting & Exhibit, American Institute of Aeronautics and Astronautics.Google Scholar
Issa, R. I. 1986 Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 62, 40–65.Google Scholar
Issa, R. I., Gosman, A. D. & Watkins, A. P. 1986 The computation of compressible and incompressible recirculating flows by a non-iterative implicit scheme. J. Comput. Phys. 62, 66–82.Google Scholar
Karino, T., Goldsmith, H. L., Motomiya, M., Mabuchi, S. & Sohara, Y. 1987 Flow patterns in vessels of simple and complex geometries. Ann. N.Y. Acad. Sci. 516, 422–441.Google Scholar
Kelley, C. T. 1995 Iterative Methods for Linear and Nonlinear Equations, Frontiers in Applied Mathematics, vol. 16. Society for Industrial and Applied Mathematics.Google Scholar
Kelley, C. T. 2003 Solving Nonlinear Equations with Newton’s Method, Fundamentals of Algorithms, vol. 1. Society for Industrial and Applied Mathematics.Google Scholar
Kockmann, N., Engler, M., Haller, D. & Woias, P. 2005 Fluid dynamics and transfer processes in bended microchannels. Heat Transfer Engng 26, 71–78.Google Scholar
Lashgari, I., Tammisola, O., Citro, V., Juniper, M. P. & Brandt, L. 2014 The planar X-junction flow: stability analysis and control. J. Fluid Mech. 753, 1–28.Google Scholar
Le Dizès, S. & Laporte, F. 2002 Theoretical predictions for the elliptical instability in a two-vortex flow. J. Fluid Mech. 471, 169–201.Google Scholar
Leibovich, S. 1978 The structure of vortex breakdown. Annu. Rev. Fluid Mech. 10, 221–246.Google Scholar
Leibovich, S. 1984 Vortex stability and breakdown: survey and extension. AIAA J. 22, 1192–1206.Google Scholar
Leweke, T. & Williamson, C. H. K. 1998 Cooperative elliptic instability of a vortex pair. J. Fluid Mech. 360, 85–119.Google Scholar
Loiseleux, T., Chomaz, J.-M. & Huerre, P. 1998 The effect of swirl on jets and wakes: linear instability of the Rankine vortex with axial flow. Phys. Fluids 10, 1120–1134.Google Scholar
Loiseleux, T., Delbende, I. & Huerre, P. 2000 Absolute and convective instabilities of a swirling jet/wake shear layer. Phys. Fluids 12, 375–380.Google Scholar
Lopez, J. M. 1990 Axisymmetric vortex breakdown. Part 1. Confined swirling flow. J. Fluid Mech. 221, 533–552.Google Scholar
Lopez, J. M. & Perry, A. D. 1992 Axisymmetric vortex breakdown. Part 3. Onset of periodic flow and chaotic advection. J. Fluid Mech. 234, 449–471.Google Scholar
Lucca-Negro, O. & O’Doherty, T. 2001 Vortex breakdown: a review. Prog. Energy Combust. Sci. 27, 431–481.Google Scholar
Mamun, C. K. & Tuckerman, L. S. 1995 Asymmetry and Hopf bifurcation in spherical Couette flow. Phys. Fluids 7, 80–91.Google Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.Google Scholar
Meliga, P., Gallaire, F. & Chomaz, J.-M. 2012 A weakly nonlinear mechanism for mode selection in swirling jets. J. Fluid Mech. 699, 216–262.Google Scholar
Oberleithner, K., Sieber, M., Nayeri, C. N., Paschereit, C. O., Petz, C., Hege, H.-C., Noack, B. R. & Wygnanski, I. 2011 Three-dimensional coherent structures in a swirling jet undergoing vortex breakdown: stability analysis and empirical mode construction. J. Fluid Mech. 679, 383–414.Google Scholar
Olendraru, C. & Sellier, A. 2002 Viscous effects in the absolute–convective instability of the Batchelor vortex. J. Fluid Mech. 459, 371–396.Google Scholar
Pierrehumbert, R. T. 1986 Universal short-wave instability of two-dimensional eddies in an inviscid fluid. Phys. Rev. Lett. 57, 2157–2159.Google Scholar
Qadri, U. A., Mistry, D. & Juniper, M. P. 2013 Structural sensitivity of spiral vortex breakdown. J. Fluid Mech. 720, 558–581.Google Scholar
Saad, Y. & Schultz, M. H. 1986 GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 7, 856–869.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows, Applied Mathematical Sciences, vol. 142. Springer.Google Scholar
Senn, S. M. & Poulikakos, D. 2004 Laminar mixing, heat transfer and pressure drop in tree-like microchannel nets and their application for thermal management in polymer electrolyte fuel cells. J. Power Sources 130, 178–191.Google Scholar
Trefethen, L. N. & Bau, D. III. 1997 Numerical Linear Algebra. Society for Industrial and Applied Mathematics.Google Scholar
Tuckerman, L. & Barkley, D. 2000 Bifurcation analysis for timesteppers. In Numerical Methods for Bifurcation Problems and Large-Scale Dynamical Systems, The IMA Volumes in Mathematics and its Applications, vol. 119, pp. 453–466. Springer.Google Scholar
Vigolo, D., Radl, S. & Stone, H. A. 2014 Unexpected trapping of particles at a T junction. Proc. Natl Acad. Sci. USA 111, 4770–4775.Google Scholar
Weller, H. H., Tabor, G., Jasak, H. & Fureby, C. 1998 A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 12, 620–631.Google Scholar
White, F. M. 2005 Viscous Fluid Flow, 3rd edn. McGraw-Hill.Google Scholar
Winters, K. H. 1987 A bifurcation study of laminar flow in a curved tube of rectangular cross-section. J. Fluid Mech. 180, 343–369.Google Scholar
Yuen, P. K. & Bau, H. H. 1996 Rendering a subcritical Hopf bifurcation supercritical. J. Fluid Mech. 317, 91–109.Google Scholar