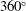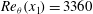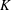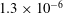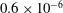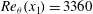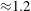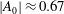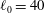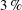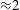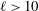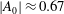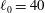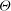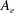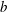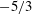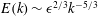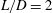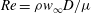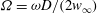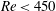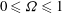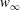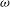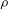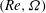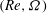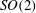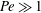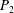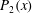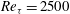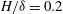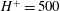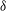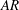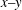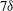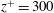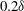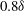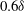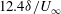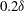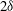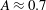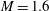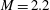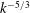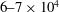We present large-eddy simulations (LES) of turbulent mixing at a perturbed, spherical interface separating two fluids of differing densities and subsequently impacted by a spherically imploding shock wave. This paper focuses on the differences between two fundamental configurations, keeping fixed the initial shock Mach number  $\approx $1.2, the density ratio (precisely
$\approx $1.2, the density ratio (precisely 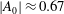 $|A_0|\approx 0.67$) and the perturbation shape (dominant spherical wavenumber
$|A_0|\approx 0.67$) and the perturbation shape (dominant spherical wavenumber 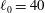 $\ell _0=40$ and amplitude-to-initial radius of 3 %): the incident shock travels from the lighter fluid to the heavy one, or inversely, from the heavy to the light fluid. In Part 1 (Lombardini, M., Pullin, D. I. & Meiron, D. I., J. Fluid Mech., vol. 748, 2014, pp. 85–112), we described the computational problem and presented results on the radially symmetric flow, the mean flow, and the growth of the mixing layer. In particular, it was shown that both configurations reach similar convergence ratios
$\ell _0=40$ and amplitude-to-initial radius of 3 %): the incident shock travels from the lighter fluid to the heavy one, or inversely, from the heavy to the light fluid. In Part 1 (Lombardini, M., Pullin, D. I. & Meiron, D. I., J. Fluid Mech., vol. 748, 2014, pp. 85–112), we described the computational problem and presented results on the radially symmetric flow, the mean flow, and the growth of the mixing layer. In particular, it was shown that both configurations reach similar convergence ratios  $\approx $2. Here, turbulent mixing is studied through various turbulence statistics. The mixing activity is first measured through two mixing parameters, the mixing fraction parameter
$\approx $2. Here, turbulent mixing is studied through various turbulence statistics. The mixing activity is first measured through two mixing parameters, the mixing fraction parameter 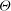 $\varTheta $ and the effective Atwood ratio
$\varTheta $ and the effective Atwood ratio 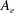 $A_e$, which reach similar late time values in both light–heavy and heavy–light configurations. The Taylor-scale Reynolds numbers attained at late times are estimated at approximately 2000 in the light–heavy case and 1000 in the heavy–light case. An analysis of the density self-correlation
$A_e$, which reach similar late time values in both light–heavy and heavy–light configurations. The Taylor-scale Reynolds numbers attained at late times are estimated at approximately 2000 in the light–heavy case and 1000 in the heavy–light case. An analysis of the density self-correlation 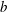 $b$, a fundamental quantity in the study of variable-density turbulence, shows asymmetries in the mixing layer and non-Boussinesq effects generally observed in high-Reynolds-number Rayleigh–Taylor (RT) turbulence. These traits are more pronounced in the light–heavy mixing layer, as a result of its flow history, in particular because of RT-unstable phases (see Part 1). Another measure distinguishing light–heavy from heavy–light mixing is the velocity-to-scalar Taylor microscales ratio. In particular, at late times, larger values of this ratio are reported in the heavy–light case. The late-time mixing displays the traits some of the traits of the decaying turbulence observed in planar Richtmyer–Meshkov (RM) flows. Only partial isotropization of the flow (in the sense of turbulent kinetic energy (TKE) and dissipation) is observed at late times, the Reynolds normal stresses (and, thus, the directional Taylor microscales) being anisotropic while the directional Kolmogorov microscales approach isotropy. A spectral analysis is developed for the general study of statistically isotropic turbulent fields on a spherical surface, and applied to the present flow. The resulting angular power spectra show the development of an inertial subrange approaching a Kolmogorov-like
$b$, a fundamental quantity in the study of variable-density turbulence, shows asymmetries in the mixing layer and non-Boussinesq effects generally observed in high-Reynolds-number Rayleigh–Taylor (RT) turbulence. These traits are more pronounced in the light–heavy mixing layer, as a result of its flow history, in particular because of RT-unstable phases (see Part 1). Another measure distinguishing light–heavy from heavy–light mixing is the velocity-to-scalar Taylor microscales ratio. In particular, at late times, larger values of this ratio are reported in the heavy–light case. The late-time mixing displays the traits some of the traits of the decaying turbulence observed in planar Richtmyer–Meshkov (RM) flows. Only partial isotropization of the flow (in the sense of turbulent kinetic energy (TKE) and dissipation) is observed at late times, the Reynolds normal stresses (and, thus, the directional Taylor microscales) being anisotropic while the directional Kolmogorov microscales approach isotropy. A spectral analysis is developed for the general study of statistically isotropic turbulent fields on a spherical surface, and applied to the present flow. The resulting angular power spectra show the development of an inertial subrange approaching a Kolmogorov-like 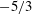 $-5/3$ power law at high wavenumbers, similarly to the scaling obtained in planar geometry. It confirms the findings of Thomas & Kares (Phys. Rev. Lett., vol. 109, 2012, 075004) at higher convergence ratios and indicates that the turbulent scales do not seem to feel the effect of the spherical mixing-layer curvature.
$-5/3$ power law at high wavenumbers, similarly to the scaling obtained in planar geometry. It confirms the findings of Thomas & Kares (Phys. Rev. Lett., vol. 109, 2012, 075004) at higher convergence ratios and indicates that the turbulent scales do not seem to feel the effect of the spherical mixing-layer curvature.