Article contents
Flow topology in the wake of a cyclist and its effect on aerodynamic drag
Published online by Cambridge University Press: 28 April 2014
Abstract
Three-dimensional flows around a full-scale cyclist mannequin were investigated experimentally to explain the large variations in aerodynamic drag that are measured as the legs are positioned around the 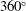 $360^\circ $ crank cycle. It is found that the dominant mechanism affecting drag is not the small variation in frontal surface area over the pedal stroke but rather due to large changes in the flow structure over the crank cycle. This is clearly shown by a series of detailed velocity field wake surveys and skin friction flow visualizations. Two characteristic flow regimes are identified, corresponding to symmetrical low-drag and asymmetrical high-drag regimes, in which the primary feature of the wake is shown to be a large trailing streamwise vortex pair, orientated asymmetrically in the centre plane of the mannequin. These primary flow structures in the wake are the dominant mechanism driving the variation in drag throughout the pedal stroke. Topological critical points have been identified on the suction surfaces of the mannequin’s back and are discussed with velocity field measurements to elucidate the time-average flow topologies, showing the primary flow structures of the low- and high-drag flow regimes. The proposed flow topologies are then related to the measured surface pressures acting on the suction surface of the mannequin’s back. These measurements show that most of the variation in drag is due to changes in the pressure distribution acting on the lower back, where the large-scale flow structures having the greatest impact on drag develop.
$360^\circ $ crank cycle. It is found that the dominant mechanism affecting drag is not the small variation in frontal surface area over the pedal stroke but rather due to large changes in the flow structure over the crank cycle. This is clearly shown by a series of detailed velocity field wake surveys and skin friction flow visualizations. Two characteristic flow regimes are identified, corresponding to symmetrical low-drag and asymmetrical high-drag regimes, in which the primary feature of the wake is shown to be a large trailing streamwise vortex pair, orientated asymmetrically in the centre plane of the mannequin. These primary flow structures in the wake are the dominant mechanism driving the variation in drag throughout the pedal stroke. Topological critical points have been identified on the suction surfaces of the mannequin’s back and are discussed with velocity field measurements to elucidate the time-average flow topologies, showing the primary flow structures of the low- and high-drag flow regimes. The proposed flow topologies are then related to the measured surface pressures acting on the suction surface of the mannequin’s back. These measurements show that most of the variation in drag is due to changes in the pressure distribution acting on the lower back, where the large-scale flow structures having the greatest impact on drag develop.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
Crouch et al. supplementary movie
Surface pressure coefficient distributions showing the development of surface pressures throughout the crank cycle.
Crouch et al. supplementary movie
Contours of out of plane streamwise vorticity throughout a full pedal stroke.
Crouch et al. supplementary movie
Three dimensional representation of the drag map in the wake of the mannequin, coloured by intensity of total drag. Drag maps represent the integrand of Maskell's equation evaluated at each probe measurement point in the wake normalised between 0-1 by the maximum value of the integrand measured throughout the crank cycle.
- 64
- Cited by




