In 1875, Lord Kelvin stated an energy-based argument for equilibrium and stability in conservative flows. The possibility of building an implementation of Kelvin’s argument, based on the construction of a simple bifurcation diagram, has been the subject of debate in the past. In this paper, we build on work from dynamical systems theory, and show that an essential requirement for constructing a meaningful bifurcation diagram is that families of solutions must be accessed through isovortical (i.e. vorticity-preserving), incompressible rearrangements. We show that, when this is the case, turning points in fluid impulse are linked to changes in the number of the positive-energy modes associated with the equilibria (and therefore in the number of modes likely to be linearly unstable). In addition, the shape of a velocity-impulse diagram, for a family of solutions, determines whether a positive-energy mode is lost or gained at the turning point. Further to this, we detect bifurcations to new solution families by calculating steady flows that have been made ‘imperfect’ through the introduction of asymmetries in the vorticity field. The resulting stability approach, which employs ‘imperfect velocity-impulse’ (IVI) diagrams, can be used to determine the number of positive-energy (likely unstable) modes for each equilibrium flow belonging to a family of steady states. As an illustration of our approach, we construct IVI diagrams for several two-dimensional flows, including elliptical vortices, opposite-signed vortex pairs (of both rotating and translating type), single and double vortex rows, as well as gravity waves. By also considering an example involving the Chaplygin–Lamb dipole, we illustrate how the stability of a specific flow may be determined, by embedding it within a properly constructed solution family. The stability data from our IVI diagrams agree precisely with results in the literature. To the best of our knowledge, for a few of the flows considered here, our work yields the first available stability boundaries. Further to this, for several of the flows that we examine, the IVI diagram methodology leads us to the discovery of new families of steady flows, which exhibit lower symmetry.
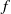 -plane
-plane