Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-22T02:06:32.588Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundary layer structure in turbulent Rayleigh–Bénard convection

Published online by Cambridge University Press:  13 June 2012

Nan Shi ,
Mohammad S. Emran  and
Jörg Schumacher
Nan Shi
Affiliation:
Institut für Thermo- und Fluiddynamik, Technische Universität Ilmenau, Postfach 100565, D-98684 Ilmenau, Germany
Mohammad S. Emran*
Affiliation:
Institut für Thermo- und Fluiddynamik, Technische Universität Ilmenau, Postfach 100565, D-98684 Ilmenau, Germany
Jörg Schumacher
Affiliation:
Institut für Thermo- und Fluiddynamik, Technische Universität Ilmenau, Postfach 100565, D-98684 Ilmenau, Germany
*
†Email address for correspondence: mohammad.emran@tu-ilmenau.de
Get access Rights & Permissions [Opens in a new window]

Abstract

The structure of the boundary layers in turbulent Rayleigh–Bénard convection is studied by means of three-dimensional direct numerical simulations. We consider convection in a cylindrical cell at aspect ratio one for Rayleigh numbers of and 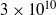at fixed Prandtl number 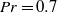. Similar to the experimental results in the same setup and for the same Prandtl number, the structure of the laminar boundary layers of the velocity and temperature fields is found to deviate from the prediction of Prandtl–Blasius–Pohlhausen theory. Deviations decrease when a dynamical rescaling of the data with an instantaneously defined boundary layer thickness is performed and the analysis plane is aligned with the instantaneous direction of the large-scale circulation in the closed cell. Our numerical results demonstrate that important assumptions of existing classical laminar boundary layer theories for forced and natural convection are violated, such as the strict two-dimensionality of the dynamics or the steadiness of the fluid motion. The boundary layer dynamics consists of two essential local dynamical building blocks, a plume detachment and a post-plume phase. The former is associated with larger variations of the instantaneous thickness of velocity and temperature boundary layer and a fully three-dimensional local flow. The post-plume dynamics is connected with the large-scale circulation in the cell that penetrates the boundary region from above. The mean turbulence profiles taken in localized sections of the boundary layer for each dynamical phase are also compared with solutions of perturbation expansions of the boundary layer equations of forced or natural convection towards mixed convection. Our analysis of both boundary layers shows that the near-wall dynamics combines elements of forced Blasius-type and natural convection.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 706 , 10 September 2012 , pp. 5 - 33
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

The first two authors contributed equally to this work.

References

1. Ahlers, G., Bodenschatz, E., Funfschilling, D. & Hogg, J. 2009a Turbulent Rayleigh–Bénard convection for a Prandtl number of 0.67. J. Fluid Mech. 641, 157–167.CrossRefGoogle Scholar
2. Ahlers, G., Grossmann, S. & Lohse, D. 2009b Heat transfer & large-scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.CrossRefGoogle Scholar
3. Bailon-Cuba, J., Emran, M. S. & Schumacher, J. 2010 Aspect ratio dependence of heat transfer and large-scale flow in turbulent convection. J. Fluid Mech. 655, 152–173.CrossRefGoogle Scholar
4. Bailon-Cuba, J. & Schumacher, J. 2011 Low-dimensional model of turbulent Rayleigh–Bénard convection in a Cartesian cell with square domain. Phys. Fluids 23, 077101.CrossRefGoogle Scholar
5. Blasius, H. 1908 Grenzschichten in Flüssigkeiten mit kleiner Reibung. Z. Math. Phys. 56, 1–37.Google Scholar
6. Brown, E. & Ahlers, G. 2009 The origin of oscillations of the large-scale circulation of turbulent Rayleigh–Bénard convection. J. Fluid Mech. 638, 383–400.CrossRefGoogle Scholar
7. Emran, M. S. & Schumacher, J. 2008 Fine-scale statistics of temperature and its derivatives in convective turbulence. J. Fluid Mech. 611, 13–34.CrossRefGoogle Scholar
8. Emran, M. S. & Schumacher, J. 2010 Lagrangian tracer dynamics in a closed cylindrical turbulent convection cell. Phys. Rev. E 82, 016303.CrossRefGoogle Scholar
9. Fuji, T. 1963 Theory of the steady laminar natural convection above a horizontal line source and a point heat source. Intl J. Heat Mass Transfer 6, 597–606.CrossRefGoogle Scholar
10. Funfschilling, D. & Ahlers, G. 2004 Plume motion and large-scale circulation in a cylindrical Rayleigh–Bénard cell. Phys. Rev. Lett. 92, 194502.CrossRefGoogle Scholar
11. Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
12. Grötzbach, G. 1983 Spatial resolution requirements for direct numerical simulation of the Rayleigh–Bénard convection. J. Comput. Phys. 49, 241–264.CrossRefGoogle Scholar
13. Hieber, C. A. 1973 Mixed convection above a heated horizontal surface. Intl J. Heat Mass Transfer 16, 769–785.CrossRefGoogle Scholar
14. Mishra, P. K., De, A. K., Verma, M. K. & Eswaran, V. 2011 Dynamics of reorientations and reversals of large-scale flow in Rayleigh–Bénard convection. J. Fluid Mech. 668, 480–499.CrossRefGoogle Scholar
15. Pohlhausen, E. 1921 Der Wärmetausch zwischen festen Körpern und Flüssigkeiten mit kleiner Reibung und kleiner Wärmeleitung. Z. Angew. Math. Mech. 1, 115–121.CrossRefGoogle Scholar
16. Prandtl, L. 1905 Über Flüssigkeitsbewegung bei sehr kleiner Reibung. In Proceedings of the Third International Mathematicians’ Congress, Heidelberg, 1904, pp. 484–491. B. G. Teubner.Google Scholar
17. du Puits, R., Resagk, C. & Thess, A. 2007a Mean velocity profile in confined turbulent convection. Phys. Rev. Lett. 99, 234504.CrossRefGoogle ScholarPubMed
18. du Puits, R., Resagk, C. & Thess, A. 2007b Breakdown of wind in turbulent thermal convection. Phys. Rev. E 75, 016302.CrossRefGoogle ScholarPubMed
19. du Puits, R., Resagk, C. & Thess, A. 2010 Measurements of the instantaneous local heat flux in turbulent Rayeigh–Bénard convection. New J. Phys. 12, 075023.CrossRefGoogle Scholar
20. Puthenveettil, B. A. & Arakeri, J. H. 2005 Plume structure in high-Rayleigh-number convection. J. Fluid Mech. 542, 217–249.CrossRefGoogle Scholar
21. Puthenveettil, B. A., Gunasegarane, G. S., Agrawal, Y. K., Schmeling, D., Bosbach, J. & Arakeri, J. H. 2011 Length of near-wall plumes in turbulent convection. J. Fluid Mech. 685, 335–364.CrossRefGoogle Scholar
22. Rotem, Z. & Claassen, L. 1969 Natural convection above unconfined horizontal surfaces. J. Fluid Mech. 39, 173–192.CrossRefGoogle Scholar
23. Schlichting, H. 1957 Boundary Layer Theory. McGraw-Hill.Google Scholar
24. Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12, 075022.CrossRefGoogle Scholar
25. Shishkina, O. & Wagner, C. 2008 Analysis of sheet-like thermal plumes in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 599, 383–404.CrossRefGoogle Scholar
26. Siggia, E. D. 1994 High Rayleigh number convection. Annu. Rev. Fluid Mech. 26, 137–168.CrossRefGoogle Scholar
27. Sparrow, E. M. & Minkowycz, W. J. 1962 Buoyancy effects on horizontal boundary-layer flow and heat transfer. Intl J. Heat Mass Transfer 5, 505–511.CrossRefGoogle Scholar
28. Stevens, R. J. A. M., Zhou, Q., Grossmann, S., Verzicco, R., Xia, K.-Q. & Lohse, D. 2012 Thermal boundary layer profiles in turbulent Rayleigh–Bénard convection in a cylindrical sample. Phys. Rev. E 85, 027301.CrossRefGoogle Scholar
29. Stewartson, K. 1958 On the free convection from a horizontal plate. Z. Angew. Math. Phys. 9, 276–282.CrossRefGoogle Scholar
30. Sun, C., Cheung, Y.-H. & Xia, K.-Q. 2008 Experimental studies of the viscous boundary layer properties in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 605, 79–113.CrossRefGoogle Scholar
31. Theerthan, S. A. & Arakeri, J. H. 1998 A model for near-wall dynamics in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 373, 221–254.CrossRefGoogle Scholar
32. van Reeuwijk, M., Jonker, H. J. J. & Hanjalić, K. 2008a Wind and boundary layers in Rayleigh–Bénard convection. Part 1. Analysis and modelling. Phys. Rev. E 77, 036311.CrossRefGoogle Scholar
33. van Reeuwijk, M., Jonker, H. J. J. & Hanjalić, K. 2008b Wind and boundary layers in Rayleigh–Bénard convection. Part 2. Boundary layer character and scaling. Phys. Rev. E 77, 036312.CrossRefGoogle Scholar
34. Verzicco, R. & Camussi, R. 2003 Numerical experiments on strongly turbulent thermal convection in a slender cylindrical cell. J. Fluid Mech. 477, 19–49.CrossRefGoogle Scholar
35. Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for three-dimensional incompressible flows in cylindrical coordinates. J. Comput. Phys. 123, 402–414.CrossRefGoogle Scholar
36. Xi, H.-D. & Xia, K.-Q. 2008a Azimuthal motion, reorientation, cessation, and reversal of the large-scale circulation in turbulent thermal convection: a comparative study in aspect ratio one and one-half geometries. Phys. Rev. E 78, 036326.CrossRefGoogle ScholarPubMed
37. Xi, H.-D. & Xia, K.-Q. 2008b Flow mode transitions in turbulent thermal convection. Phys. Fluids 20, 055104.CrossRefGoogle Scholar
38. Zhou, Q., Stevens, R. J. A. M., Sugiyama, K., Grossmann, S., Lohse, D. & Xia, K.-Q. 2010 Prandtl–Blasius temperature and velocity boundary-layer profiles in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 664, 297–312.CrossRefGoogle Scholar
39. Zhou, Q., Sugiyama, K., Stevens, R. J. A. M., Grossmann, S., Lohse, D. & Xia, K.-Q. 2011 Horizontal structures of velocity and temperature boundary layers in two-dimensional numerical turbulent Rayleigh–Bénard convection. Phys. Fluids 23, 125104.CrossRefGoogle Scholar
40. Zhou, Q., Sun, C. & Xia, K.-Q. 2007 Morphological evolution of thermal plumes in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 98, 074501.CrossRefGoogle ScholarPubMed
41. Zhou, Q. & Xia, K.-Q. 2010a Measured instantaneous viscous boundary layer in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 104, 104301.CrossRefGoogle ScholarPubMed
42. Zhou, Q. & Xia, K.-Q. 2010b Physical and geometrical properties of thermal plumes in turbulent Rayleigh–Bénard convection. New J. Phys. 12, 075006.CrossRefGoogle Scholar