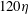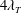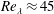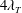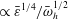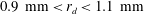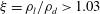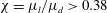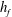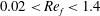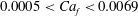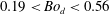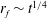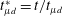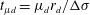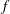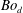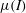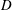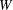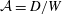Papers
A quantitative assessment of viscous asymmetric vortex pair interactions
-
- Published online by Cambridge University Press:
- 14 September 2017, pp. 1-30
-
- Article
- Export citation
The scaling of straining motions in homogeneous isotropic turbulence
-
- Published online by Cambridge University Press:
- 14 September 2017, pp. 31-64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Computational analysis of vortex dynamics and performance enhancement due to body–fin and fin–fin interactions in fish-like locomotion
-
- Published online by Cambridge University Press:
- 14 September 2017, pp. 65-88
-
- Article
- Export citation
Stability of three-dimensional columnar convection in a porous medium
-
- Published online by Cambridge University Press:
- 14 September 2017, pp. 89-111
-
- Article
- Export citation
Algebraic disturbance growth by interaction of Orr and lift-up mechanisms
-
- Published online by Cambridge University Press:
- 14 September 2017, pp. 112-126
-
- Article
- Export citation
Electrohydrodynamics of viscous drops in strong electric fields: numerical simulations
-
- Published online by Cambridge University Press:
- 14 September 2017, pp. 127-152
-
- Article
- Export citation
A Lagrangian fluctuation–dissipation relation for scalar turbulence. Part I. Flows with no bounding walls
-
- Published online by Cambridge University Press:
- 14 September 2017, pp. 153-189
-
- Article
- Export citation
The ‘hanging flag’ problem: on the heaving motion of a thin filament in the limit of small flexural stiffness
-
- Published online by Cambridge University Press:
- 14 September 2017, pp. 190-213
-
- Article
- Export citation
Control of viscous instability by variation of injection rate in a fluid with time-dependent rheology
-
- Published online by Cambridge University Press:
- 14 September 2017, pp. 214-235
-
- Article
- Export citation
A Lagrangian fluctuation–dissipation relation for scalar turbulence. Part II. Wall-bounded flows
-
- Published online by Cambridge University Press:
- 14 September 2017, pp. 236-279
-
- Article
- Export citation
Radiation of internal waves from groups of surface gravity waves
-
- Published online by Cambridge University Press:
- 15 September 2017, pp. 280-303
-
- Article
- Export citation
Film spreading from a miscible drop on a deep liquid layer
-
- Published online by Cambridge University Press:
- 14 September 2017, pp. 304-327
-
- Article
- Export citation
Circulation control in magnetohydrodynamic rotating flows
-
- Published online by Cambridge University Press:
- 15 September 2017, pp. 328-344
-
- Article
- Export citation
Interfacial pattern selection in defiance of linear growth
-
- Published online by Cambridge University Press:
- 19 September 2017, pp. 345-363
-
- Article
- Export citation
Lagrangian transport by breaking surface waves
-
- Published online by Cambridge University Press:
- 19 September 2017, pp. 364-391
-
- Article
- Export citation
Direct numerical simulation of a self-similar adverse pressure gradient turbulent boundary layer at the verge of separation
-
- Published online by Cambridge University Press:
- 20 September 2017, pp. 392-419
-
- Article
- Export citation
The dynamics of partial cavity formation, shedding and the influence of dissolved and injected non-condensable gas
-
- Published online by Cambridge University Press:
- 20 September 2017, pp. 420-458
-
- Article
- Export citation
Experiments on, and discrete and continuum simulations of, the discharge of granular media from silos with a lateral orifice
-
- Published online by Cambridge University Press:
- 21 September 2017, pp. 459-485
-
- Article
- Export citation
JFM Papers
Experimental investigation of flow-induced vibration of a rotating circular cylinder
-
- Published online by Cambridge University Press:
- 21 September 2017, pp. 486-511
-
- Article
- Export citation
Papers
Vorticity transport mechanisms governing the development of leading-edge vortices
-
- Published online by Cambridge University Press:
- 22 September 2017, pp. 512-537
-
- Article
- Export citation