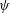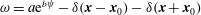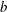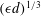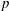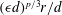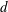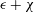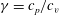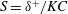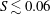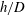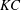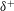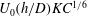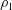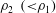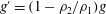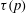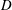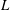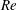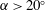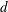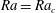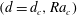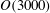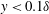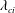JFM Perspectives
Undulatory and oscillatory swimming
-
- Published online by Cambridge University Press:
- 04 July 2019, P1
-
- Article
-
- You have access
- HTML
- Export citation
JFM Rapids
Steady point vortex pair in a field of Stuart-type vorticity
-
- Published online by Cambridge University Press:
- 10 July 2019, R1
-
- Article
- Export citation
A note on acoustic turbulence
-
- Published online by Cambridge University Press:
- 18 July 2019, R2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Focus on Fluids
Solving the inertial particle equation with memory
-
- Published online by Cambridge University Press:
- 03 July 2019, pp. 1-4
-
- Article
-
- You have access
- HTML
- Export citation
JFM Papers
Effect of finite conductivity on the nonlinear behaviour of an electrically charged viscoelastic liquid jet
-
- Published online by Cambridge University Press:
- 03 July 2019, pp. 5-37
-
- Article
- Export citation
Topology-based characterization of compressibility effects in mixing layers
-
- Published online by Cambridge University Press:
- 03 July 2019, pp. 38-75
-
- Article
- Export citation
On low-Prandtl-number convection in an inclined layer of liquid mercury
-
- Published online by Cambridge University Press:
- 03 July 2019, pp. 76-101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mean velocity, spreading and entrainment characteristics of weak bubble plumes in unstratified and stationary water
-
- Published online by Cambridge University Press:
- 03 July 2019, pp. 102-130
-
- Article
- Export citation
Weak shock reflection in channel flows for dense gases
-
- Published online by Cambridge University Press:
- 03 July 2019, pp. 131-157
-
- Article
- Export citation
Cylinder wakes in shallow oscillatory flow: the coastal island wake problem
-
- Published online by Cambridge University Press:
- 04 July 2019, pp. 158-184
-
- Article
- Export citation
Inertial gravity current produced by the drainage of a cylindrical reservoir from an outer or inner edge
-
- Published online by Cambridge University Press:
- 04 July 2019, pp. 185-209
-
- Article
- Export citation
Swimming sheet in a density-stratified fluid
-
- Published online by Cambridge University Press:
- 04 July 2019, pp. 210-234
-
- Article
- Export citation
Vertical shear alters chemical front speed in thin-layer flows
-
- Published online by Cambridge University Press:
- 04 July 2019, pp. 235-262
-
- Article
- Export citation
Turbulent temperature fluctuations in a closed Rayleigh–Bénard convection cell
-
- Published online by Cambridge University Press:
- 04 July 2019, pp. 263-284
-
- Article
- Export citation
Similarity solutions and viscous gravity current adjustment times
-
- Published online by Cambridge University Press:
- 04 July 2019, pp. 285-298
-
- Article
- Export citation
Flow instabilities in the wake of a circular cylinder with parallel dual splitter plates attached
-
- Published online by Cambridge University Press:
- 04 July 2019, pp. 299-338
-
- Article
- Export citation
Optimal viscous damping of vibrating porous cylinders
-
- Published online by Cambridge University Press:
- 09 July 2019, pp. 339-358
-
- Article
- Export citation
Weakly nonlinear mode interactions in spherical Rayleigh–Bénard convection
-
- Published online by Cambridge University Press:
- 09 July 2019, pp. 359-390
-
- Article
- Export citation
Wind–wave coupling study using LES of wind and phase-resolved simulation of nonlinear waves
-
- Published online by Cambridge University Press:
- 09 July 2019, pp. 391-425
-
- Article
- Export citation
Experimental study on dominant vortex structures in near-wall region of turbulent boundary layer based on tomographic particle image velocimetry
-
- Published online by Cambridge University Press:
- 09 July 2019, pp. 426-454
-
- Article
- Export citation