Article contents
Steady point vortex pair in a field of Stuart-type vorticity
Published online by Cambridge University Press: 10 July 2019
Abstract
A new family of exact solutions to the two-dimensional steady incompressible Euler equation is presented. The solutions provide a class of hybrid equilibria comprising two point vortices of unit circulation – a point vortex pair – embedded in a smooth sea of non-zero vorticity of ‘Stuart-type’ so that the vorticity  $\unicode[STIX]{x1D714}$ and the stream function
$\unicode[STIX]{x1D714}$ and the stream function 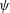 $\unicode[STIX]{x1D713}$ are related by
$\unicode[STIX]{x1D713}$ are related by 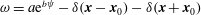 $\unicode[STIX]{x1D714}=a\text{e}^{b\unicode[STIX]{x1D713}}-\unicode[STIX]{x1D6FF}(\boldsymbol{x}-\boldsymbol{x}_{0})-\unicode[STIX]{x1D6FF}(\boldsymbol{x}+\boldsymbol{x}_{0})$, where
$\unicode[STIX]{x1D714}=a\text{e}^{b\unicode[STIX]{x1D713}}-\unicode[STIX]{x1D6FF}(\boldsymbol{x}-\boldsymbol{x}_{0})-\unicode[STIX]{x1D6FF}(\boldsymbol{x}+\boldsymbol{x}_{0})$, where  $a$ and
$a$ and 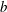 $b$ are constants. We also examine limits of these new Stuart-embedded point vortex equilibria where the Stuart-type vorticity becomes localized into additional point vortices. One such limit results in a two-real-parameter family of smoothly deformable point vortex equilibria in an otherwise irrotational flow. The new class of hybrid equilibria can be viewed as continuously interpolating between the limiting pure point vortex equilibria. At the same time the new solutions continuously extrapolate a similar class of hybrid equilibria identified by Crowdy (Phys. Fluids, vol. 15, 2003, pp. 3710–3717).
$b$ are constants. We also examine limits of these new Stuart-embedded point vortex equilibria where the Stuart-type vorticity becomes localized into additional point vortices. One such limit results in a two-real-parameter family of smoothly deformable point vortex equilibria in an otherwise irrotational flow. The new class of hybrid equilibria can be viewed as continuously interpolating between the limiting pure point vortex equilibria. At the same time the new solutions continuously extrapolate a similar class of hybrid equilibria identified by Crowdy (Phys. Fluids, vol. 15, 2003, pp. 3710–3717).
JFM classification
- Type
- JFM Rapids
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 8
- Cited by



